Downloaded 219 times
More Related Content
![[PRML] パターン認識と機械学習（第3章：線形回帰モデル）](https://cdn.slidesharecdn.com/ss_thumbnails/prmlchapter3-171003081954-thumbnail.jpg?width=640&height=640&fit=bounds)
![学振特別研究員になるために～知っておくべき10のTips～[平成29年度申請版]](https://cdn.slidesharecdn.com/ss_thumbnails/10tips29-160403152412-thumbnail.jpg?width=640&height=640&fit=bounds)
![学振特別研究員になるために～知っておくべき10のTips～[平成28年度申請版]](https://cdn.slidesharecdn.com/ss_thumbnails/random-150226210930-conversion-gate02-thumbnail.jpg?width=640&height=640&fit=bounds)
PRML Chapter 5
- 1. パターン認識と機械学習 第5章 ニューラルネットワーク D2 大上雅史 PRML輪講 2012/4/25
- 2. 目次 第5章 ニューラルネットワーク 5.1 フィードフォワードネットワーク関数 5.2 ネットワーク訓練 5.3 誤差逆伝播 http://www2.edu.ipa.go.jp/gz/a-cg/a-800/a-810/a-811.jpg 4/25/2012
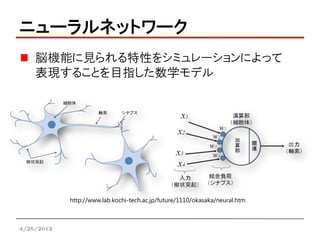
- 3. ニューラルネットワーク 脳機能に見られる特性をシミュレーションによって 表現することを目指した数学モデル http://www.lab.kochi-tech.ac.jp/future/1110/okasaka/neural.htm 4/25/2012
- 4. 線形モデルの復讐復習 例：多項式曲線フィッティング 4/25/2012
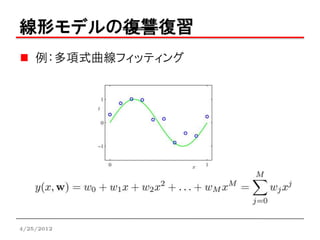
- 5. 線形モデルの復習 一般形 • Áj(x) ：基底関数 • Á0(x) = 1, w0はバイアス項 多項式曲線フィッティングでは 4/25/2012
- 6. 回帰問題とクラス分類問題 回帰問題 クラス分類問題 • f( )を非線形活性化関数という • f( )の例： 4/25/2012
- 7. ニューラルネットワークの線形モデル 線形和の重み係数wを訓練する 基本的なニューラルネットワーク 4/25/2012
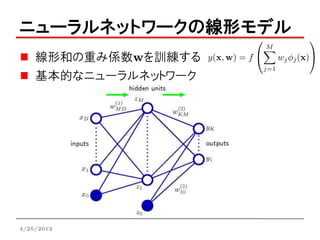
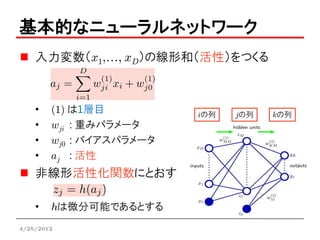
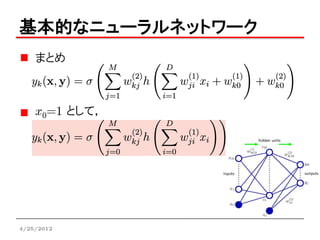
- 8. 基本的なニューラルネットワーク 入力変数（x1,…, xD）の線形和（活性）をつくる • (1) は1層目 iの列 jの列 kの列 • wji : 重みパラメータ • wj0 : バイアスパラメータ • aj : 活性 非線形活性化関数にとおす • hは微分可能であるとする 4/25/2012
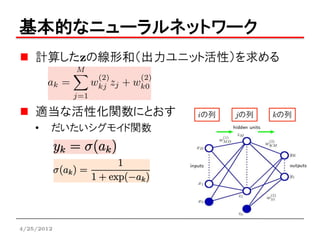
- 9. 基本的なニューラルネットワーク 計算したzの線形和（出力ユニット活性）を求める 適当な活性化関数にとおす iの列 jの列 kの列 • だいたいシグモイド関数 4/25/2012
- 10. 基本的なニューラルネットワーク まとめ x0=1 として， 4/25/2012
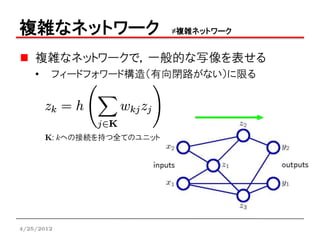
- 11. 複雑なネットワーク ≠複雑ネットワーク 複雑なネットワークで，一般的な写像を表せる • フィードフォワード構造（有向閉路がない）に限る K: kへの接続を持つ全てのユニット 4/25/2012
- 12. ネットワーク訓練 ネットワークパラメータwを決める • 決め方→二乗和誤差の最小化 定式化 • 入力ベクトル • 目標ベクトル • 誤差関数 4/25/2012
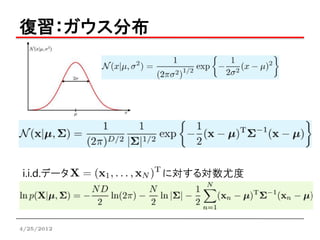
- 13. ネットワーク訓練 ネットワーク出力の確率的解釈が大事 回帰問題として，実数値目標変数tを考える • tは平均がxに依存するガウス分布に従う • 尤度関数 4/25/2012
- 14. 復習：ガウス分布 i.i.d.データ に対する対数尤度 4/25/2012
- 15. ネットワーク訓練 誤差関数（負の対数尤度） • ニューラルネットワークの研究では尤度最大化より 誤差関数最小化の方が常套手段 • 誤差関数を最小化して最尤推定解を求める （尤度最大化と等価である） 4/25/2012
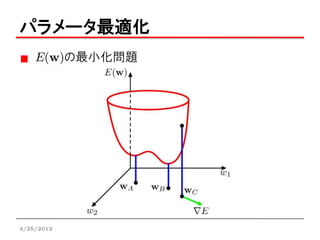
- 16. ネットワーク訓練 wを求める→E(w)の最小化 • y(xn,w)の非線形性により正確には局所解 wMLが求まったらbは誤差関数最小化で求められる • をbで微分して0と置く 4/25/2012
- 17. ネットワーク訓練 目標変数が複数（K個）の場合（t→t） • 条件付き確率が独立，ノイズの分散が共通であると仮定 • wML：尤度最大化→二乗和誤差関数の最小化 証明 4/25/2012
- 18. ネットワーク訓練 • bは誤差関数最小化によって求められる • K は目標変数の数 4/25/2012
- 19. ネットワーク訓練 2クラス分類問題の場合 • t=1がクラスC1，t=0がクラスC2 • ロジスティックシグモイド関数を活性化関数とする • 目標の条件付き分布（ベルヌーイ分布） • 誤差関数（負の対数尤度） 交差エントロピー誤差関数 4/25/2012
- 20. ネットワーク訓練 K個の異なる2クラス分類問題の場合 • 活性化関数・・・ロジスティックシグモイド関数 • K個の出力を持つネットワーク • 誤差関数（負の対数尤度） 交差エントロピー誤差関数 4/25/2012
- 21. ネットワーク訓練 標準的なKクラス分類問題の場合 • 1-of-K符号化法で表されるとする • ネットワーク出力は • 誤差関数（負の対数尤度） • 出力ユニットの活性化関数はソフトマックス関数 4/25/2012
- 22. ネットワーク訓練 まとめ 活性化関数 誤差関数 回帰問題 線形 二乗和 （独立な多数の） ロジスティックシグモイド 交差エントロピー 2クラス分類問題 多クラス分類問題 ソフトマックス 多クラス交差エントロピー ロジスティックシグモイド 2クラス分類問題 交差エントロピー or ソフトマックス 4/25/2012
- 23. パラメータ最適化 E(w)の最小化問題 4/25/2012
- 24. 局所二次近似 重み空間内の点 の周りでのE(w)の二次近似 • : 勾配 • ： ヘッセ行列 の近くでの勾配の局所近似（二次近似式の微分） 4/25/2012
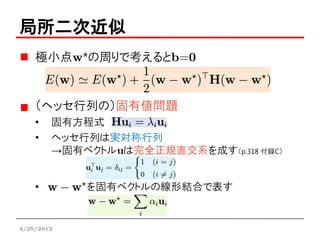
- 25. 局所二次近似 極小点w*の周りで考えるとb=0 （ヘッセ行列の）固有値問題 • 固有方程式 • ヘッセ行列は実対称行列 →固有ベクトルuは完全正規直交系を成す（p.318 付録C） • を固有ベクトルの線形結合で表す 4/25/2012
- 26. 局所二次近似 以上を用いて誤差関数を書き換える 4/25/2012
- 27. 行列の正定値性 行列Aが正定値である⇔ 行列Aが正定値である⇔Aの全ての固有値が正 証明 4/25/2012
- 28. 誤差関数の等高線 固有空間上の誤差関数の等高線は楕円となる 4/25/2012
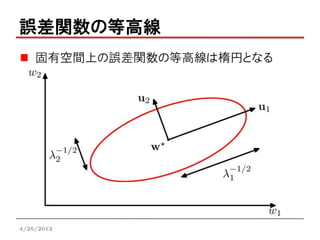
- 29. 誤差関数の等高線 固有空間上の誤差関数の等高線は楕円となる 証明 4/25/2012
- 30. 局所二次近似 ヘッセ行列Hの での値が正定値 ⇔ は極小点である 証明⇒ 証明⇐ 4/25/2012
- 31. 勾配情報の利用 誤差曲面はbとHで決定される • bの独立なパラメータ数・・・W個 (Wはwの次元) • Hの独立なパラメータ数・・・W(W+1)/2個 • 極小点を求めるために必要な点の数 O(W2) • 極小点の評価に必要なステップ数 O(W) の評価でW個の情報が得られる • 勾配情報を用いれば 4/25/2012
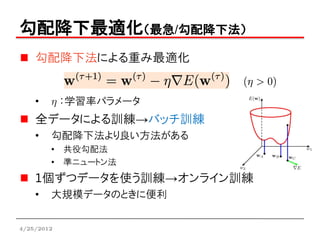
- 32. 勾配降下最適化（最急/勾配降下法） 勾配降下法による重み最適化 • h ：学習率パラメータ 全データによる訓練→バッチ訓練 • 勾配降下法より良い方法がある • 共役勾配法 • 準ニュートン法 1個ずつデータを使う訓練→オンライン訓練 • 大規模データのときに便利 4/25/2012
- 33. 確率的勾配降下法（オンライン版勾配降下法） 確率的勾配降下法の誤差関数 • ：各データ点についての誤差 確率的勾配降下法の更新式 • hのスケジューリングが重要 • 大域的最適解が得られるかも • Eの停留点は必ずしもEiの停留点ではないから 4/25/2012
- 34. バックプロパゲーション 誤差逆伝播法（バックプロパゲーション） ×伝搬 ○伝播 ×でんぱん ○でんぱ • 誤差関数の勾配を効率良く評価する方法 wikipediaより 1. ネットワークの出力と与えられたサンプルの最適解を比較する． 各出力ユニットについて誤差を計算する． 2. 個々のユニットの期待される出力値と重み， 要求された出力と実際の出力の差（誤差）を計算する． 3. 各ユニットの重みを誤差が小さくなるよう調整する． 4. より大きな重みで接続された前層のユニットに誤差の責任があると決める． 5. そのユニットのさらに前層のユニットついて同様の処理を行う バックプロパゲーション 伝言ゲームにおいて，最後の人から逆方向に「元々はどういう言葉だったの？」 と伝言することで誤りを修正するアルゴリズム．（朱鷺の社より） 4/25/2012
- 35. 誤差関数微分の評価 単純な線形モデルで考える • 出力ykが入力変数xiの線形和 • 誤差関数 ※ 入力パターンnの誤差関数の重みに関する勾配 • 接続i-jの出力側の誤差信号と入力側の変数の積の形 4/25/2012
- 36. 誤差関数の偏微分の計算 計算（添字に注意，(n)に意味はないが補足的に） 4/25/2012
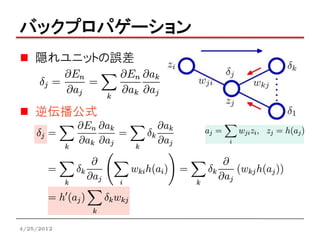
- 37. バックプロパゲーション 一般のフィードフォワードネットワークの場合 • ユニットの出力 • 微分する（添字nを省略） ：誤差 • 正準連結関数を活性化関数に用いた出力ユニットでは 4/25/2012
- 38. 復習：正準連結関数 一般化線形モデル • ：活性化関数 • ：連結関数 正準連結関数 • 条件付き確率分布を指数型分布族から選ぶ • 活性化関数を正準連結関数から選ぶ →誤差関数の微分が誤差(yn-tn)と特徴ベクトルjの積になる 4/25/2012
- 39. バックプロパゲーション 隠れユニットの誤差 逆伝播公式 4/25/2012
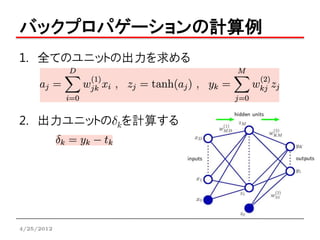
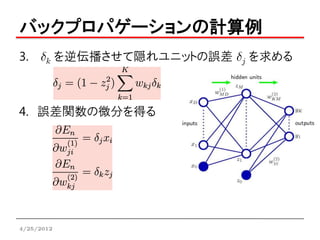
- 40. バックプロパゲーション まとめ（誤差逆伝播） 1. 入力ベクトルxnを入れ，全てのユニットの出力を求める （順伝播） 2. 全ての出力ユニットの誤差 dk を評価する 3. dk を逆伝播させて全ての隠れユニットの誤差 dj を得る 4. 必要な微分を評価する 4/25/2012
- 41. バックプロパゲーション 補足 • バッチ手法の場合 →全体の誤差関数の微分は全てのパターンの総和 • ユニットごとに活性化関数が違う場合 →特に変わらない （ユニットごとのhを用いて計算すれば良い） 4/25/2012
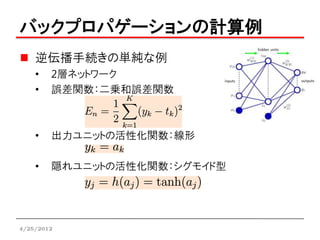
- 42. バックプロパゲーションの計算例 逆伝播手続きの単純な例 • 2層ネットワーク • 誤差関数：二乗和誤差関数 • 出力ユニットの活性化関数：線形 • 隠れユニットの活性化関数：シグモイド型 4/25/2012
- 43. tanh関数の性質 定義 微分 4/25/2012
- 44.
- 45. バックプロパゲーションの計算例 3. dk を逆伝播させて隠れユニットの誤差dj を求める 4. 誤差関数の微分を得る 4/25/2012
- 46. バックプロパゲーションの効率 順伝播の計算量・・・ • の計算量 • 結合が非常に疎である場合を除くと 重み数≫ユニット数 • 逆伝播も同様 4/25/2012
- 47. 誤差関数の数値微分 数値微分（有限幅差分）の利用 • 前進差分（前方差分） • 中央差分（中心差分） • 誤差項が小さくなるが，前進差分の倍くらいの計算量が必要 数値微分は計算量が • 逆伝播公式の結果の正当性を数値微分で確認する，など 4/25/2012
- 48. 数値微分の誤差の評価 前進差分 • 誤差の評価 中央差分 • 誤差の評価 4/25/2012
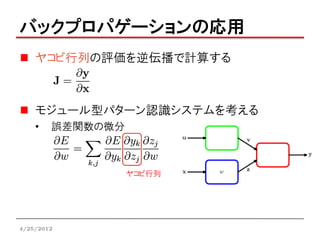
- 49. バックプロパゲーションの応用 ヤコビ行列の評価を逆伝播で計算する モジュール型パターン認識システムを考える • 誤差関数の微分 ヤコビ行列 4/25/2012
- 50. ヤコビ行列のバックプロパゲーション ヤコビ行列の要素を変形 微分を計算 出力ユニット • シグモイド活性化関数 • ソフトマックス関数 4/25/2012