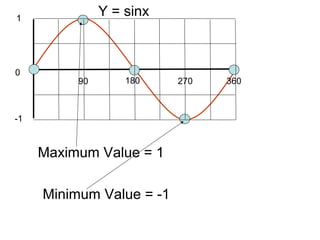
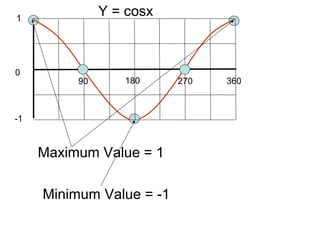
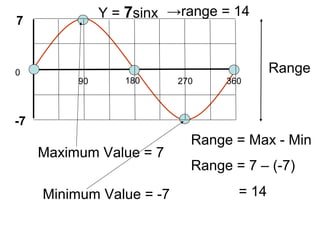
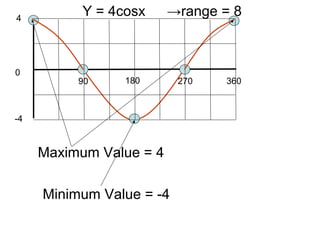
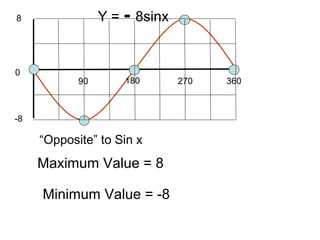
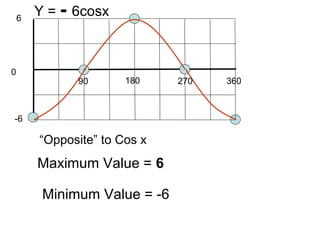
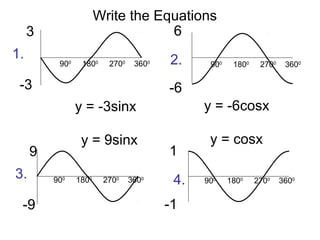
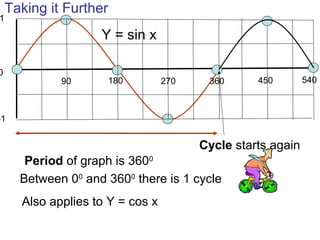
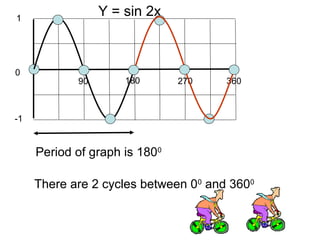
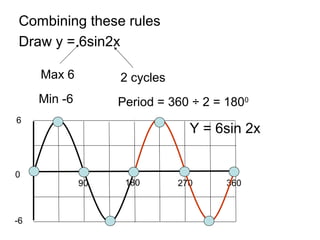
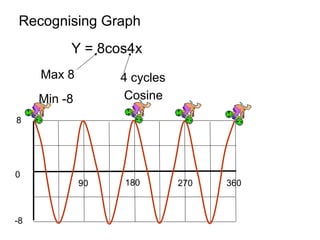
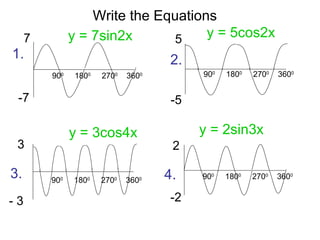
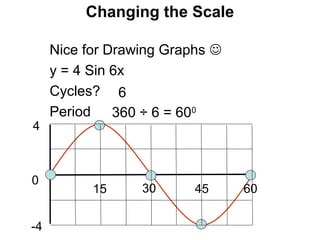
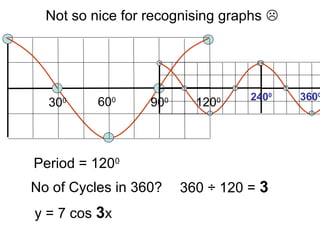
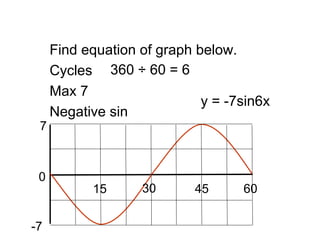
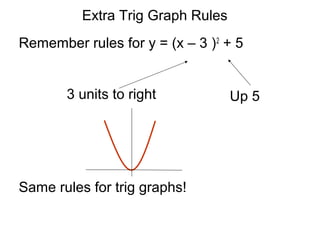
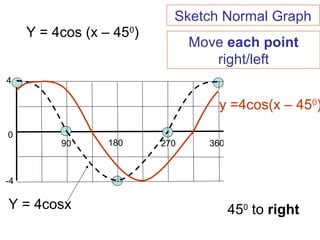
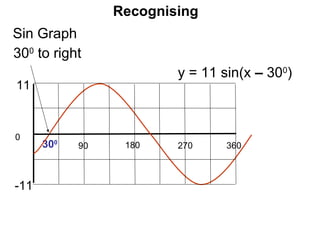
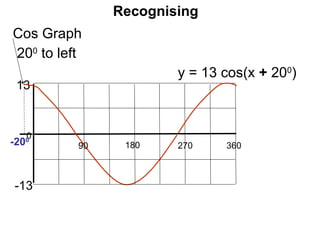
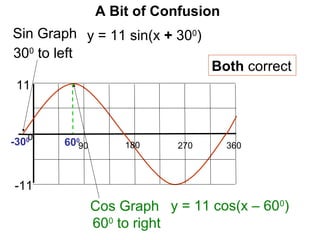
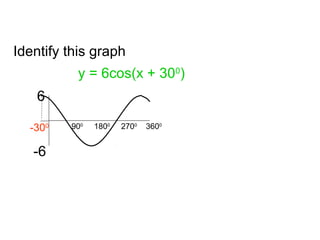
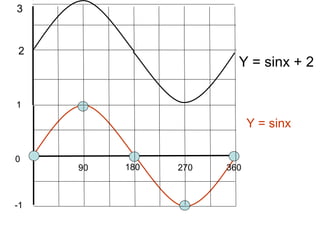
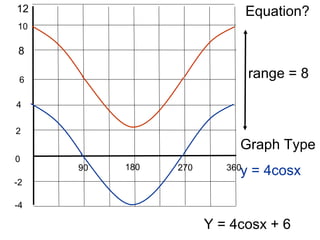
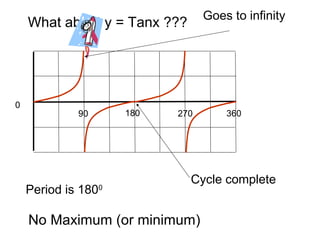
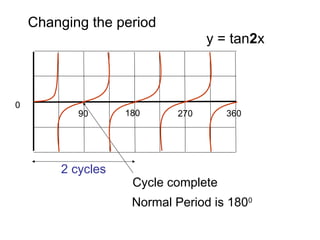
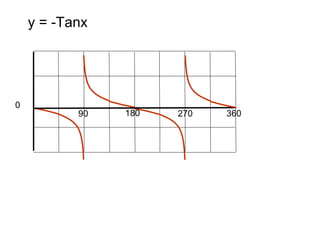
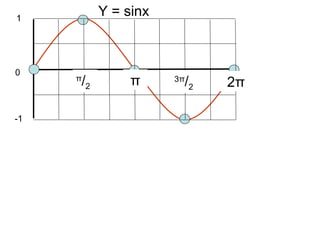
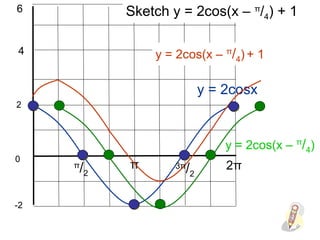
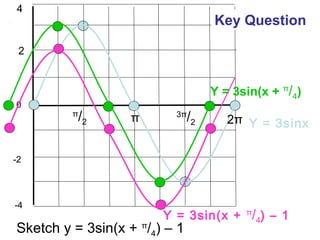
This document provides a review of trigonometric graphs including how to draw and identify them. It discusses the maximum and minimum values, range, period and number of cycles for sin and cos graphs. It also covers shifting graphs horizontally or vertically and combining trig functions with constants. Examples are provided to illustrate identifying trig graphs from their equations and sketching shifted or combined trig graphs.

1. Block 3
Trigonometric Graphs

2. What is to be learned?
• A reminder of how to draw and identify trig
graphs.
• Take it a bit further.

3. 90 180 270 360
1
0
-1
Y = sinx
Maximum Value = 1
Minimum Value = -1

4. 90 180 270 360
1
0
-1
Y = cosx
Maximum Value = 1
Minimum Value = -1

5. 90 180 270 360
7
0
-7
Y = 7sinx
Maximum Value = 7
Minimum Value = -7
Range = Max - Min
Range = 7 – (-7)
= 14
→range = 14
Range

6. 90 180 270 360
4
0
-4
Y = 4cosx
Maximum Value = 4
Minimum Value = -4
→range = 8

7. 90 180 270 360
8
0
-8
Y = - 8sinx
Maximum Value = 8
Minimum Value = -8
“Opposite” to Sin x

8. 90 180 270 360
6
0
-6
Y = - 6cosx
Maximum Value = 6
Minimum Value = -6
“Opposite” to Cos x

9. 900
1800
2700
3600
900
1800
2700
3600
3
-3
6
-6
Write the Equations
1. 2.
y = -3sinx y = -6cosx
y = 9sinx y = cosx
3. 4.
9
-9
1
-1
900
1800
2700
3600
900
1800
2700
3600

10. 90 180 270 360
1
0
-1
Y = sin x
540450
Period of graph is 3600
Cycle starts again
Also applies to Y = cos x
Between 00
and 3600
there is 1 cycle
Taking it Further

11. 90 180 270 360
1
0
-1
Y = sin 2x
Period of graph is 1800
There are 2 cycles between 00
and 3600

12. Combining these rules
Draw y = 6sin2x
Max 6
Min -6
2 cycles
Period = 360 ÷ 2 = 1800
90 180 270 360
6
0
-6
Y = 6sin 2x

13. Recognising Graph
Max 8
Min -8
4 cycles
90 180 270 360
8
0
-8
Y = 8cos4x
Cosine

14. 900
1800
2700
3600 900
1800
2700
3600
900
1800
2700
3600 900
1800
2700
3600
7
-7
5
-5
3
- 3
2
-2
Write the Equations
1. 2.
3. 4.
y = 7sin2x y = 5cos2x
y = 3cos4x y = 2sin3x

15. Changing the Scale
Nice for Drawing Graphs 
y = 4 Sin 6x
Cycles?
Period
6
360 ÷ 6 = 600
15 30 45 60
4
0
-4

16. 300 600
900
1200
7
Not so nice for recognising graphs 
Period = 1200
No of Cycles in 360? 360 ÷ 120 = 3
y = 7 cos 3x
2400 3600

17. Find equation of graph below.
Cycles
Max 7
Negative sin
360 ÷ 60 = 6
15 30 45 60
7
0
-7
y = -7sin6x

18. Remember rules for y = (x – 3 )2
+ 5
Same rules for trig graphs!
3 units to right Up 5
Extra Trig Graph Rules

19. 90 180 270 360
4
0
-4
Y = 4cos (x – 450
)
450
Y = 4cosx 450
to right
Sketch Normal Graph
Move each point
right/left
y =4cos(x – 450
)

20. 90 180 270 360
11
0
-11
Recognising
Sin Graph
300
to right
y = 11 sin(x – 300
)
300

21. 90 180 270 360
13
0
-13
Recognising
Cos Graph
200
to left
y = 13 cos(x + 200
)
-200

22. 90 180 270 360
11
0
-11
A Bit of Confusion
Sin Graph
300
to left
y = 11 sin(x + 300
)
-300
600
Cos Graph
600
to right
y = 11 cos(x – 600
)
Both correct

23. 6
-6
y = 6cos(x + 300
)
-300
Identify this graph
900
1800
2700
3600

24. 90 180 270 360
1
0
-1
Y = sinx + 2
Y = sinx
2
3

25. 90 180 270 360
4
0
-4
Y = 4cosx + 6
8
12
range = 8
Graph Type
y = 4cosx
2
6
10
-2
Equation?

26. 90 180 270 360
0
No Maximum (or minimum)
What about y = Tanx ???
Goes to infinity
Cycle complete
Period is 1800

27. 90 180 270 360
0
Changing the period
Cycle complete
Normal Period is 1800
2 cycles
y = tan2x

28. 90 180 270 360
0
y = -Tanx

29. Also
Can now use radians!

30. 90 180 270 360
1
0
-1
Y = sinx
π
/2 π 3π
/2 2π

31. Trigonometric Graphs
Follow all the same rules as other function
graphs.
Range is handy for identifying (max – min)
e.g. for y = 7sinx →range = 14

32. π
/2
π 2π
2
0
-2
y = 2cos(x – π
/4)
4
6
y = 2cosx
Sketch y = 2cos(x – π
/4) + 1
y = 2cos(x – π
/4) + 1
3π
/2

33. 0
-2
-4
Sketch y = 3sin(x + π
/4) – 1
Y = 3sinx
2
4
Y = 3sin(x + π
/4)
Y = 3sin(x + π
/4) – 1
Key Question
2π
3π
/2ππ
/2