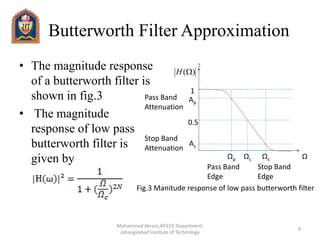
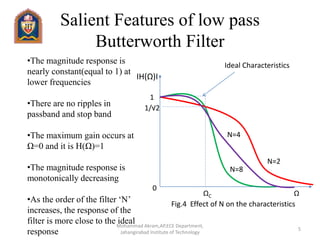
The document outlines the design and characteristics of IIR digital Butterworth filters, explaining ideal low pass filter characteristics and approximations. It details the magnitude response of Butterworth filters, emphasizes their key features like constancy in lower frequencies and monotonic decrease, and provides step-by-step methods for designing digital Butterworth filters using impulse invariance and bilinear transformation. Additionally, it includes equations for calculating filter order, cutoff frequency, poles, and system transfer functions.

1. Designing of IIR Digital Filters
Butterworth Filter
1
Mohammad Akram,AP,ECE Department,
Jahangirabad Institute of Technology

2. Analog Filter Approximation
• Ideal low pass filter:
• It passes frequencies till
cut off frequency fc.
• After that it blocks all the
Frequencies as shown in the
fig.1 ffc
|H(f)|
Pass band Stop band
Fig.1 Characteristics of a low pass filter
2
Mohammad Akram,AP,ECE Department,
Jahangirabad Institute of Technology

3. Approximation in ideal
characteristics
• Several approximations have been
made as shown in fig. 2:
• fp is passband edge frequency at
which reduction has been started
• fs is stopband edge frequency
after which filter blocks all the
frequencies.
• fc lies between fs and fp
• fc is 3db down to the maximum
value in the log scale and 1/√2 of
the maximum value in the
absolute scale
• ∆f is the transition frequency from
pass band to stop band
Fig.2 Approximation in ideal characteristics
f
)( fH
-
3dB
1
fp fc fs
∆f
3
Mohammad Akram,AP,ECE Department,
Jahangirabad Institute of Technology

4. Butterworth Filter Approximation
• The magnitude response
of a butterworth filter is
shown in fig.3
• The magnitude
response of low pass
butterworth filter is
given by
1
Ap
0.5
As
Ωp Ωc Ωs Ω
Pass Band
Attenuation
Stop Band
Attenuation
Pass Band
Edge
Stop Band
Edge
Fig.3 Manitude response of low pass butterworth filter
2
)(H
4
Mohammad Akram,AP,ECE Department,
Jahangirabad Institute of Technology

5. Salient Features of low pass
Butterworth Filter
IH(Ω)I
Ω
1
1/√2
0
ΩC
Ideal Characteristics
N=2
N=4
N=8
Fig.4 Effect of N on the characteristics
•The magnitude response is
nearly constant(equal to 1) at
lower frequencies
•There are no ripples in
passband and stop band
•The maximum gain occurs at
Ω=0 and it is H(Ω)=1
•The magnitude response is
monotonically decreasing
•As the order of the filter ‘N’
increases, the response of the
filter is more close to the ideal
response 5
Mohammad Akram,AP,ECE Department,
Jahangirabad Institute of Technology

6. Designing using Butterworth
Approximation
•Design equation and design steps:
Let A p=Attenuation in passband
As=Attenuation in stop band
Ωp=Passband edge frequency
Ωc=Cut off frequency
Ωs=Stopband edge frequency
•In the problem the specifications of required digital filter is given and it
will be asked to design a particular discrete time butterworth filter.The
following steps should be used:
Step I:From the given specifications of digital filter, obtain equivalent
analog filter as follows:
(a) For Impulse Invariance method:
TS


6
Mohammad Akram,AP,ECE Department,
Jahangirabad Institute of Technology

7. (b) For bilinear transformation method:
Here Ω = Frequency of analog filter
ω=Frequency of digital filter
Ts = Sampling Time
Step II: Calculate the order N of filter using the equation,
2
tan
2 
TS

)log(
1
1
1
2
1
log
2
1
2









































P
S
PA
AS
N
7
Mohammad Akram,AP,ECE Department,
Jahangirabad Institute of Technology

8. If specifications are given in decibels(dB) then use the equation
Step III: Calculation of cut off frequency (Ωc)
The cut off frequency (Ωc) of analog filter is calculated as:
(a) For Impulse Invariance method:
For Bilinear Transformation method:





















P
S
dB
dB
A
A
N
P
S
log
1
1
log
2
1 10
10
)(1.0
)(1.0
TS
C
C

2
tan
2 C
S
C
T

8
Mohammad Akram,AP,ECE Department,
Jahangirabad Institute of Technology

9. When ωc is not given then use the equation
And if specifications are in dB then use
Step IV: Calculate the poles using
,k=0,1,2,……N-1
If the poles are complex conjugate then organize the poles ( P k) as complex
conjugate pairs that means s1 and , s2 and etc.







 
1
1
2
2
1
AP
N
P
c
110
1.0

  AP
P
C
 
eP N
kNj
ck
2
12 

s
*
1 s
*
2
9
Mohammad Akram,AP,ECE Department,
Jahangirabad Institute of Technology

10. Step V: Calculate the system transfer function of analog filter using,
And if poles are complex conjugate then,
Step VI: Design the digital filter using impulse invariance method or
bilinear transformation method.
  ...
)(
21
pp ss
sH
N
c

 
    ssss ssss
sH
N
c
*
22
*
11
)(

 
10
Mohammad Akram,AP,ECE Department,
Jahangirabad Institute of Technology

11. 11
Mohammad Akram,AP,ECE Department,
Jahangirabad Institute of Technology