Molecular diffusion
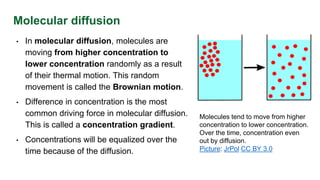
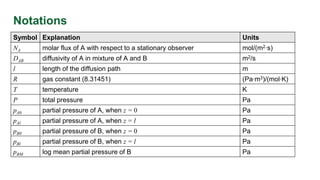
This document provides an overview of molecular diffusion, detailing its mechanisms driven primarily by concentration gradients, and introduces Fick's laws to describe the molar flux in binary mixtures. It covers various types of diffusion, diffusivity coefficients, and examples of gas diffusion calculations under steady-state conditions. The project is funded by the EU's Horizon 2020 programme and references several academic sources for further reading.
More Related Content
Similar to Molecular diffusion
More from South-Eastern Finland University of Applied Sciences
Molecular diffusion
- 1. This project hasreceived funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 869993. Molecular diffusion
- 2. Diffusion • Diffusion israndom movement of an individual component through the mixture. • The most common driving force for diffusion is the concentration difference. Diffusion can also be driven by other gradients, e.g. temperature or pressure. Diffusion can also be caused by external force. Then it is called forced diffusion. • Net movement of molecules is called molecular diffusion.
- 3. Molecular diffusion • Inmolecular diffusion, molecules are moving from higher concentration to lower concentration randomly as a result of their thermal motion. This random movement is called the Brownian motion. • Difference in concentration is the most common driving force in molecular diffusion. This is called a concentration gradient. • Concentrations will be equalized over the time because of the diffusion. Molecules tend to move from higher concentration to lower concentration. Over the time, concentration even out by diffusion. Picture: JrPol CC BY 3.0
- 4. Fick’s first law •Fick’s first law is the basic law of diffusion for binary mixtures. It expresses the molar flux of A (JA) with respect to an observer moving with the molar average velocity. • DAB is a constant, specified to substances, called diffusivity or diffusion coefficient. • In practice, the molar flux NA with respect to a stationary observer is more useful. • For ideal gas mixtures, we can write it in terms of pressure. CA = pA/RT and C = P/RT 𝐽𝐴 = −𝐷𝐴𝐵 𝑑𝐶𝐴 𝑑𝑧 𝑁𝐴 = (𝑁𝐴 + 𝑁𝐵) 𝐶𝐴 𝐶 − 𝐷𝐴𝐵 𝑑𝐶𝐴 𝑑𝑧 JA = molar flux (mol/(m2∙s)) DAB = diffusion coefficient of A in a mixture of A and B (m2/s) dCA = concentration difference of A (mol/m3) dz = difference in length (m) ⇒ 𝑁𝐴= (𝑁𝐴 + 𝑁𝐵) 𝑝𝐴 𝑃 − 𝐷𝐴𝐵 𝑅𝑇 𝑑𝑝𝐴 𝑑𝑧 Bulk flow + molecular diffusion
- 5. Diffusion coefficients DAB •The value of diffusivity DAB depends upon pressure, temperature and composition. Experimental diffusivity values can be found from literature. • There are also several equations to estimate diffusivities with specific combinations. These are not studied in this course. • Diffusivities are generally higher for gases than for liquids. Value ranges: • Diffusivity of gases: 0.5 x 10-5 – 7.0 x 10-5 m2/s • Diffusivity of liquids: 10-10 – 10-9 m2/s • Diffusivity of solids: 10-14 – 10-10 m2/s • If the gas mixture is ideal, mutual diffusivities of A and B are equal: DAB = DBA • In other cases, it is important to remember that those values are not necessary equal.
- 6. Different types ofmolecular diffusion • There are several types of molecular diffusion and they can be divided into different groups by different bases. • Based on phase: Molecular diffusion in gases, liquids and solids • Based on state: Unsteady state and steady state molecular diffusion • Based on amount of components: Binary and multicomponent systems • Based on area: Diffusion through constant area or variable area • Based on rates: Equimolar and non-equimolar diffusion • Based on reactions: Chemical reaction or no reaction • Two most common and simplest situation are covered in this module: • steady state equimolar counter diffusion • steady state diffusion of A through stagnant B
- 7. Steady state moleculardiffusion through a constant area Equimolar counter diffusion NA = -NB NA + NB = 0 Diffusion of A through stagnant B NB = 0 Example: Bromine gas diffusing into the surrounding air. Equal amount of air is diffusing into the tube. Example: Water is evaporating from the tube. The amount of substituting air is insignificant. 𝑁𝐴 = (𝑁𝐴 + 𝑁𝐵) 𝐶𝐴 𝐶 − 𝐷𝐴𝐵 𝑑𝐶𝐴 𝑑𝑧 ⇒ 𝑵𝑨 = −𝑫𝑨𝑩 𝒅𝑪𝑨 𝒅𝒛 𝑁𝐴 = (𝑁𝐴 + 𝑁𝐵) 𝐶𝐴 𝐶 − 𝐷𝐴𝐵 𝑑𝐶𝐴 𝑑𝑧 ⇒ 𝑵𝑨= 𝑵𝑨 𝑪𝑨 𝑪 − 𝑫𝑨𝑩 𝒅𝑪𝑨 𝒅𝒛 Pictures: Screenshots from the video: https://youtu.be/03wJkMIiac0 (Lund University)
- 8. The integrated equationsfor steady state diffusion Equimolar counter diffusion NA = -NB NA + NB = 0 Diffusion of A through stagnant B NB = 0 in G A S E S In terms of partial pressures In terms of mole fractions in L I Q U I D S In terms of concentrations In terms of mole fractions 𝑁𝐴 = 𝐷𝐴𝐵 𝑙 𝐶𝐴0 − 𝐶𝐴𝑙 𝑁𝐴 = 𝐷𝐴𝐵 𝑙 𝜌 𝑀 𝑥𝐴0 − 𝑥𝐴𝑙 𝑁𝐴 = 𝐷𝐴𝐵𝑃 𝑅𝑇𝑙 𝑦𝐴0 − 𝑦𝐴𝑙 𝑁𝐴 = 𝐷𝐴𝐵 𝑅𝑇𝑙 𝑝𝐴0 − 𝑝𝐴𝑙 𝑁𝐴 = 𝐷𝐴𝐵 𝑙𝑥𝐵𝑀 𝐶𝐴0 − 𝐶𝐴𝑙 𝑁𝐴 = 𝐷𝐴𝐵 𝑙𝑥𝐵𝑀 𝜌 𝑀 𝑥𝐴0 − 𝑥𝐴𝑙 𝑁𝐴 = 𝐷𝐴𝐵𝑃 𝑅𝑇𝑙𝑝𝐵𝑀 𝑝𝐴0 − 𝑝𝐴𝑙 𝑝𝐵𝑀 = 𝑝𝐵𝑙 − 𝑝𝐵0 ln 𝑝𝐵𝑙 𝑝𝐵0 𝑥𝐵𝑀 = 𝑥𝐵𝑙 − 𝑥𝐵0 ln 𝑥𝐵𝑙 𝑥𝐵0 𝑁𝐴 = 𝐷𝐴𝐵𝑃 𝑅𝑇𝑙 𝑙𝑛 1 − 𝑦𝐴𝑙 1 − 𝑦𝐴0
- 9. Notations Symbol Explanation Units NAmolar flux of A with respect to a stationary observer mol/(m2∙s) DAB diffusivity of A in mixture of A and B m2/s l length of the diffusion path m R gas constant (8.31451) (Pa∙m3)/(mol∙K) T temperature K P total pressure Pa pA0 partial pressure of A, when z = 0 Pa pAl partial pressure of A, when z = l Pa pB0 partial pressure of B, when z = 0 Pa pBl partial pressure of B, when z = l Pa pBM log mean partial pressure of B Pa
- 10. Notations Symbol Explanation Units CA0molar concentration of A, when z = 0 mol/m3 CAl molar concentration of A, when z = l mol/m3 yA0 mole fraction of A in gaseuous mixture, when z = 0 mol/mol yAl mole fraction of A in gaseuous mixture, when z = l mol/mol xA0 mole fraction of A in a liquid solution, when z = 0 mol/mol xAl mole fraction of A in a liquid solution, when z = l mol/mol xBM log mean molar concentration of B in liquid solution mol/mol ρ density of the solution kg/m3 M molecular weight of the solution kg/mol ρ/M average molar concentration of the liquid mol/m3
- 11. Example: Diffusion ofA through stagnant B • Oxygen (O2) is diffusing through carbon monoxide at 0 °C (steady state conditions, carbon monoxide nondiffusing). The total pressure is 100 kPa. The partial pressure of oxygen at two planes 2.00 mm apart is, respectively 13 kPa and 6.5 kPa. The diffusivity is 1.87 x 10-5 m2/s. Calculate the NA. 𝑁𝐴 = 𝐷𝐴𝐵𝑃 𝑅𝑇𝑙𝑝𝐵𝑀 𝑝𝐴0 − 𝑝𝐴𝑙 = 1.87 ∙ 10−5 ∙ 100000 8.31451 ∙ 273.15 ∙ 0.002 ∙ 90211 13000 − 6500 = 0.0297 mol m2 ∙ s DAB = 1.87∙10-5 m2/s P = 100 000 Pa R = 8.31451 (Pa∙m3)/(mol∙K) T = 273.15 K l = 0.002 m pA0 = 13 000 Pa pAl = 6 500 Pa pB0 = 100 000 Pa – 13 000 Pa = 87 000 Pa pBl = 100 000 Pa – 6 500 Pa = 93 500 Pa 𝑝𝐵𝑀 = 𝑝𝐵𝑙 − 𝑝𝐵0 ln 𝑝𝐵𝑙 𝑝𝐵0 = 93 500 Pa − 87 000 Pa ln 93 500 Pa 87 000 Pa = 90 210.9745 Pa
- 12. Example continuing • Let'scontinue with the previous example. How many kilograms of oxygen diffuses in one hour in that situation, if the diffusing area is 10 m2? NA was calculated in the previous slide. NA = 0.0297 mol/(m2∙s). 𝑛oxygen = 0.0297 mol m2∙s ∙ 10 m2 ∙ 3600 s = 1069.2 mol 𝑀oxygen = 2 ∙ 16.00 g mol = 32.00 g mol 𝑚oxygen = 𝑛𝑀 = 1069.2 mol ∙ 32.00 g mol = 34214.4 g ≈ 𝟑𝟒. 𝟐 𝐤𝐠 Moles of oxygen per 10 m2 in 1 hour: Molar mass of oxygen: Mass of oxygen:
- 13. Summary • Molecular diffusionis the net movement of molecules. • Fick’s law determines the molar flux of A (JA) in the binary mixture of A and B, with respect to an observer moving with the molar average velocity. • The molar flux NA with respect to a stationary observer is more useful. • The equation can be integrated and expressed in terms of mole fractions, concentrations or partial pressures. • The most common situations are equimolar counter diffusion and diffusion of A through nondiffusing B. 𝐽𝐴 = −𝐷𝐴𝐵 𝑑𝐶𝐴 𝑑𝑧 𝑁𝐴 = (𝑁𝐴 + 𝑁𝐵) 𝐶𝐴 𝐶 − 𝐷𝐴𝐵 𝑑𝐶𝐴 𝑑𝑧 Bulk flow + molecular diffusion DAB = diffusivity (diffusion coefficient)
- 14. This project hasreceived funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 869993. References Benitez, J. 2016. Principles and Modern Applications of Mass Transfer Operations. Wiley, pp. 16-17, 38-56. Dutta, B. K. 2007. Principles of mass transfer and separation processes. New Delhi: Prentice-Hall, pp. 11-30, 42-44. Treybal, R. E. 1980. Mass-transfer operations. 3rd ed. Auckland: McGraw-Hill, pp. 22-38. Videos: • Equimolar counter diffusion: https://youtu.be/0HhQhj6HvSk • Steady state molecular diffusion: https://youtu.be/Iw-uTLT1LcA • Fick’s law explained: https://youtu.be/Hmfnolr47Zw