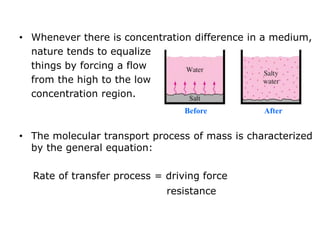
The document introduces mass transfer as a fundamental process involving the movement of mass between locations influenced by concentration gradients. It outlines various mass transfer operations, such as diffusion, distillation, and drying, which occur in different phases (gas, liquid, solid) and are characterized by driving forces like concentration, temperature, and pressure gradients. Key principles, including Fick's law of diffusion and examples of calculation in steady-state scenarios, are discussed to illustrate the mechanics of mass transfer.

1. Introduction to mass transfer
W kalala

2. Introduction
• Three fundamental transfer processes:
i) Momentum transfer
ii) Heat transfer
iii) Mass transfer

3. Mass transfer is the net movement of mass from one location,
usually meaning stream, phase, fraction or component, to
another, WITH OR WITHOUT Phase change
Many processes operate by a change in the composition of a phase
because of the diffusion of one component in another.
Such processes are known as diffusional or mass transfer processes.
Distillation, dissolution, drying, and crystallization provide examples.
The movement is usually from a region of high concentration to a region
of low concentration under the tinfluence of the concentration gradient.
 In all cases, diffusion is the result of a difference in the concentration of
the diffusing substance, this component moving influence of the
concentration gradient.

4. In mass transfer operations, two immiscible phases are
normally present, one or both of which are fluid.
 In general, these phases are in relative movement and
the rate at which a component is transferred from one
phase to the other is greatly influenced by the bulk
movement imposed upon the fluids.
In most drying processes, for example, water vapor
diffuses from a saturated layer in contact with the drying
surface into a turbulent air stream.

5. • Mass transfer may occur in a gas mixture, a
liquid solution or solid.
• Mass transfer occurs whenever there is a
gradient in the concentration of a species.
• The basic mechanisms are the same
whether the phase is a gas, liquid, or solid.

7. Intro
• Filtration Dissolution
• Sedimentation
• Centrifugation
• Distillation
• Diffusion
• Osmosis
• Drying
• Mixing

8. In mass transfer operations, two immiscible phases
are normally present , one or both of which are
fluids. The phases have relative movement and the
rate at which one component is transferred from
one phase to the other is greatly influenced by the
bulk movement imposed on the fluid.
e.g. in drying, water vapor diffuses from a saturated
layer in contact with drying surface into turbulent
air stream.
Consider two compartments containing gas A and
Gas B separated by a partition:
A B

9. Diffusion phenomena
• Fick’s law: linear relation between the rate of
diffusion of chemical species and the concentration
gradient of that species.
• Thermal diffusion: Diffusion due to a temperature
gradient. Usually negligible unless the temperature
gradient is very large.
• Pressure diffusion: Diffusion due to a pressure
gradient. Usually negligible unless the pressure
gradient is very large.

10. • Whenever there is concentration difference in a medium,
nature tends to equalize
things by forcing a flow
from the high to the low
concentration region.
• The molecular transport process of mass is characterized
by the general equation:
Rate of transfer process = driving force
resistance
Before After

11. • Consider a tank that is divided into two equal
parts by a partition.
• Initially, the left half of the tank contains
nitrogen N2 gas while the right half contains
O2 at the same temperature and pressure.
• When the partition is removed the N2
molecules will start diffusing into the air while
the O2 molecules diffuse into the N2.
• If we wait long enough, we will have a
homogeneous mixture of N2 and O2 in the
tank.
Example of Mass Transfer Processes

12. • The rate of diffusion Na of A into B or Nb of B
into A :
• Where D = Diffusivity of A in B ( it is a property
proportional molecular velocity, temperature and
pressure of the gases )
• N is in Moles per m2 per second. It is negative because
the concentration is decreasing
• This is Fick’s Law.
dz
dc
D
J A
AB
AZ 

*

14. Example 1
A mixture of He and N2 gas is contained in a
pipe at 298 K and 1 atm total pressure which
is constant throughout. At one end of the pipe
at point 1 the partial pressure pA1 of He is 0.6
atm and at the other end 0.2 m pA2 = 0.2 atm.
Calculate the flux of He at steady state if DAB
of the He-N2 mixture is 0.687 x 10-4 m2/s.

15. Solution
• Since a total pressure P is constant, the c is constant, where c is as follows
for a gas according to the perfect gas law:
• Where n is kg mol A plus B, V is volume in
T is temperature in K,
R is 8314.3 m3.Pa/kg mol.K or R is 82.057 x 10-3 cm3. atm/g. mol. K,
and c is kg mol A plus B/m3.
• For steady state the flux J*Az in Eq.(6.1-3) is constant. Also DAB for gas is
constant. Rearranging Eq. (6.1-3) and integrating.

16. • Also, from the perfect gas law, pAV=nART, and
This is the final equation to use, which is in a form equation used
for gases. Partial pressures are pA1 = 0.6 atm = 0.6 x 1.01325 x
105 = 6.04 x 104 Pa and pA2 = 0.2 atm = 0.2 x 1.01325 x 105 =
2.027 x 104 Pa. Then, using SI units,
Equation 2

17. • If pressures in atm are used with SI unit,
• Other driving forces (besides concentration
differences) for diffusion also occur because of
temperature, pressure, electrical potential, and other
gradients.

18. Example 2
Ammonia gas (A) is diffusing through a uniform tube
0.10 m long containing N2 gas (B) at 1.0132 x 105 Pa
pressure and 298 K.
1. At point 1, pA1 = 1.013 x 104 Pa and
at point 2, pA2 = 0.507 x 104 Pa.
The diffusivity DAB = 0.230 x 10-4 m2/s.
(a) Calculate the flux J*A at steady state
(b) Repeat for J*B

19. Solution
• Equation 2 can be used, where P = 1.0132 x 105 Pa, z2-z1 =
0.10 m, and T = 298 K. Substituting into the equation, for part
(a),
• Rewriting Eq. for component B for part (b) and noting that pB1
= P – pA1 = 1.01325 x 105 – 1.013 x 104 = 9.119 x 104 Pa and
pB2 = P – pA2 = 1.01325 x 105 – 0.507 x 104 = 9.625 x 104 Pa.
• The negative for J*B means the flux goes from point 2 to point
1.

20. Convection Mass Transfer
• When a fluid flowing outside a solid surface in forced convection motion, rate
of convective mass transfer is given by:
kc - mass transfer coefficient (m/s)
cL1 - bulk fluid conc.
cLi - conc of fluid near the solid surface
• Kc depend on:
1. system geometry
2. Fluid properties
3. Flow velocity
)
( 1 Li
L
c
A c
c
k
N 
