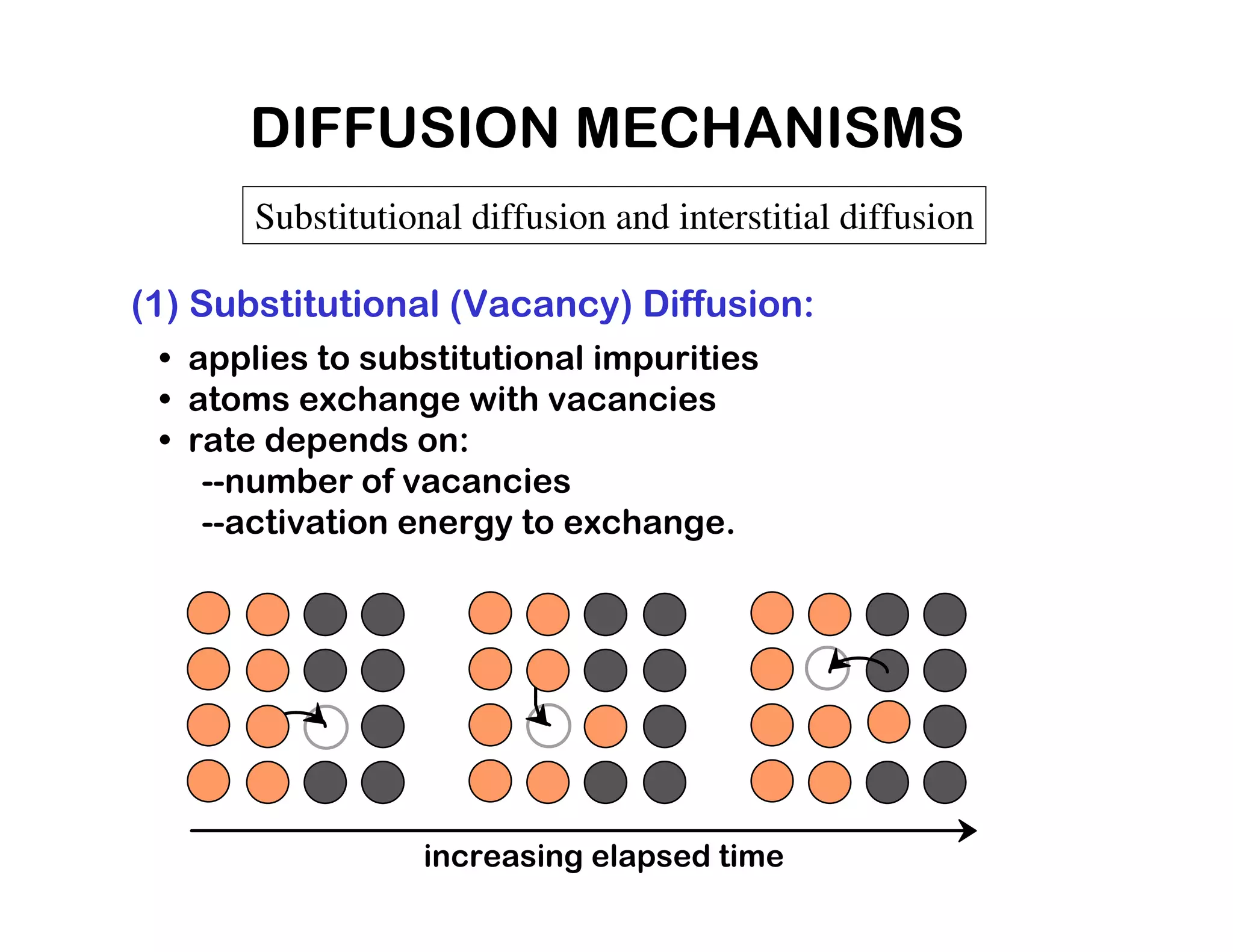
This document summarizes key aspects of diffusion in solids: 1) Diffusion occurs due to a concentration gradient, which provides a driving force for atoms to move from high to low concentration regions. 2) Diffusion is an important part of materials processing techniques like case hardening and doping of semiconductors. 3) The rate of diffusion depends on factors like temperature, structure, and the diffusion mechanism (e.g. substitutional vs. interstitial). Fick's laws can be used to model and predict diffusion rates.

1. Chapter 6
DIFFUSION IN SOLIDS
• How does diffusion occur?
• Why is it an important part of processing?
• How can the rate of diffusion be predicted for
some simple cases?
• How does diffusion depend on structure
and temperature?

2. Driving force for movement
In general, force is a position derivative of energy (F = - dE/dr).
In other words, if there is any energy difference in space,
there is a force which will act on matters - Force will move things.
(ex1) Potential energy by gravity:
Apple falls from high altitude (high potential energy) to
low altitude (low potential energy).
(ex2) Drift current by battery (electrical potential energy).
(ex3) Atoms move from high concentration (high chemical potential)
to low concentration (low chemical potential) → Diffusion!
* Concentration gradient is the driving force.
(well, it is chemical potential energy to be precise.
Concentration gradient is not sufficient condition for diffusion.)

3. Interdiffusion
• Interdiffusion: In an alloy, atoms tend to migrate
from regions of large concentration.
Initially After some time
Cu Ni
100% 100%
0 0
Concentration Profiles Concentration Profiles

4. DIFFUSION MECHANISMS
Substitutional diffusion and interstitial diffusion
(1) Substitutional (Vacancy) Diffusion:
• applies to substitutional impurities
• atoms exchange with vacancies
• rate depends on:
--number of vacancies
--activation energy to exchange.
increasing elapsed time

5. Vacancy Diffusion
• Simulation of
interdiffusion
across an interface:
• Rate of substitutional
diffusion depends on:
--vacancy concentration
--frequency of jumping.
Temperature dependent.

6. (2) Interstitial Diffusion
tetrahedral octahedral
• Applies to interstitial
(small) impurities FCC
(O, N, C, etc).
• More rapid than vacancy
diffusion
BCC
Why?

7. Self-Diffusion
• Self-diffusion: In an elemental solid, atoms also migrate
through diffusion. Driving force can be
described by more general thermodynamic
potential. This type of diffusion in the
crystalline material generally occurs
through substitutional diffusion.
Label some atoms After some time
C
C
A D
A
D
B
B

8. PROCESSING USING DIFFUSION (1)
• Case Hardening:
--Diffuse carbon atoms
into the host iron atoms
at the surface.
--Example of interstitial
diffusion is a case
hardened gear.
• Result: The "Case" is
-- hard to deform: C atoms
"lock" planes from shearing.
-- hard to crack: C atoms put
the surface in compression.

9. PROCESSING USING DIFFUSION (2)
• Doping Silicon with P for n-type semiconductors:
• Process:
0.5mm
1. Deposit P rich
layers on surface.
magnified image of a computer chip
silicon
2. Heat it.
3. Result: Doped
light regions: Si atoms
semiconductor
regions.
light regions: Al atoms
silicon

10. MODELING DIFFUSION: FLUX
• Flux: Amount of matter that passes
through unit area per unit time.
1 dM  kg   atoms
J= ⇒  2  or  2 
A dt m s   m s 
• Flux can be measured for:
--vacancies x-direction
--host (A) atoms
--impurity (B) atoms
• Flux is directional Quantity. Unit area A
y J through
y
which
Jx atoms
Jz move.
x
z

11. MODELING DIFFUSION: FLUX
• Flux can be also given by
Flux = (conductivity) x (driving force)
(ex) Electrical current (I) = (1/R) x V (Ohm’s law)
- For diffusion, the conductivity is called
‘diffusivity’ or ‘diffusion coefficient’,
and it is typically presented by the symbol, D.
- Driving force is concentration gradient, ∆C/∆x.
- One important issue when you face with the diffusion problem
is whether or not things change as a function of time.
Steady state diffusion (nothing changes.)
Non steady-state diffusion (flux & conc. profile change.)

12. STEADY STATE DIFFUSION
(Fick’s First Law)
• Steady State:
Steady State:
Jx(left) Jx(right) J x(left) = Jx(right)
x
Concentration, C, in the box doesn’t change w/time.
dC
• Apply Fick's First Law: J x = −D
dx
 dC   dC 
• If Jx)left = Jx)right , then   = 
 dx  left  dx  right
• Result: the slope, dC/dx, must be constant
(i.e., slope doesn't vary with position and time)!

13. EX: STEADY STATE DIFFUSION
3
g/m
• Steel plate at . 2k 3
=1 g/m
700C with C1 .8k
=0
C2
geometry Carbon Steady State =
rich straight line!
shown:
gas Carbon
deficient
gas
D=3x10-11m2/s
0 x1 x2
10
• Q: How much 5m
m
m
m
carbon transfers
from the rich to C2 − C1 = −9 kg
J = −D 2.4 × 10
the deficient side? x2 − x1 m2s

14. DIFFUSION AND TEMPERATURE
• Diffusivity increases with T.
pre-exponential [m2/s] (see Table 5.2, Callister 6e)
activation energy
 Q  [J/mol],[eV/mol]
diffusivity D = Do exp − d  (see Table 5.2, Callister 6e )
 RT 
gas constant [8.31J/mol-K]
• Experimental Data:
1500
1000
600
300
T(C)
10-8 D has exp. dependence on T
C
in
D (m2/s) Ci Recall: Vacancy does also!
γ-
nα
Fe
-Fe Dinterstitial >> Dsubstitutional
10-14 C in α-Fe Cu in Cu
Zn
Al in Al
Fe
C in γ-Fe
in Cun α-
Al
Fe in α-Fe
Cu in Fe
Fe -Fe
in
in
Fe in γ-Fe
Al
γ
i
Zn in Cu
Cu
10-20
0.5 1.0 1.5 2.0 1000K/T

16. NON STEADY STATE DIFFUSION
(Fick’s Second Law)
dx
• Concentration profile,
J(left) J(right)
C(x), changes
w/ time. Concentration,
C, in the box
• To conserve matter: • Fick's First Law:
J(right) − J(left) = dC dC
− J = −D or
dx dt dx
dJ = dC dJ = d2 C (if D does
− −D not vary
dx dt dx dx2 with x)
(Temperature
equate is fixed here.)
• Governing Eqn.:
dC d2C
=D 2 Fick’s Second Law
dt dx

17. NON STEADY STATE DIFFUSION
• Copper diffuses into a bar of aluminum.
Surface conc.,
Cs of Cu atoms Al bar
pre-existing conc., C o of copper atoms
C(x,t)
Cs Boundary condition:
t=0, C=C0 at 0≤x ≤∞
t
t2 3
t>0, C=Cs at x=0
to t1
C=C0 at x=∞
Co
x=0 position, x
• General solution
for C(x,t): C(x, t) − Co =  x 
1 − erf  
 2 Dt 
Fick’s 2nd law is Cs − Co
the differential equation. "error function"

18. NON STEADY STATE DIFFUSION
(ex1) – EXAMPLE PROBLEM 6.2 (page 162)
Carburizing steel with methane gas (source for C)
Q. How long will it take to achieve a carbon content of 0.80 wt%
at a position 0.5mm below the surface of the steel piece under
given Cs and Co condition?
A. The question gave you C(x,t) and x. Need to find t.
C(x, t) − Co =  x 
1 − erf  
 2 Dt 
Cs − Co
"error function"
z

19. PROCESSING QUESTION
• Copper diffuses into a bar of aluminum.
• 10 hours at 600C gives desired C(x).
• How many hours would it take to get the same C(x)
if we processed at 500C?
Key point 1: C(x,t500C) = C(x,t600C).
Key point 2: Both cases have the same Co and Cs.
• Result: Dt should be held constant.
C(x,t) − Co  x 
= 1 − erf  
 2Dt 
(Dt)500ºC =(Dt)600ºC
Cs − Co
5.3x10-13m2/s 10hrs
(Dt)600 Note: values
• Answer: t 500 = = 110 hr of D are
-14m2/s
D500 provided here.
4.8x10

20. SUMMARY
Diffusion FASTER for... Diffusion SLOWER for...
• open crystal structures • close-packed structures
• lower melting T materials • higher melting T materials
(self diffusion) (self diffusion)
• materials w/secondary • materials w/covalent
bonding (self diffusion) bonding (self diffusion)
• smaller diffusing atoms • larger diffusing atoms
• cations (small) • anions (big)
• lower density materials • higher density materials