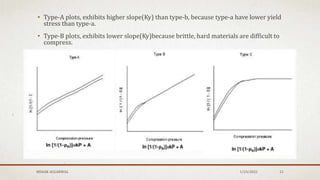
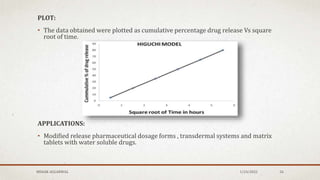
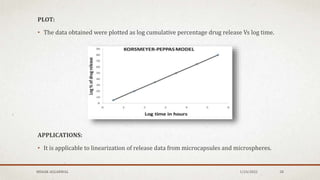
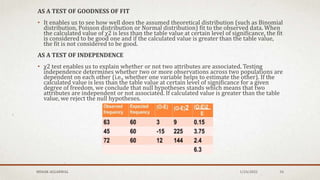
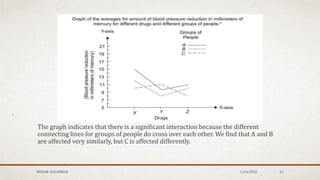
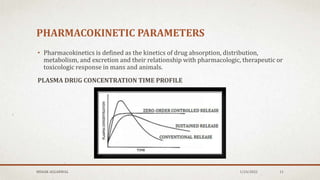
The document discusses the study of consolidation and various parameters relevant to pharmacokinetics and drug release mechanisms. It covers essential theories and methods such as diffusion parameters, dissolution, Heckel plots, and the applications of similarity factors f1 and f2 in comparing dissolution profiles. Additionally, it includes statistical concepts like standard deviation, chi-square tests, and the importance of understanding linearity in significance testing.















![HECKEL PLOTS
• The Heckel analysis is a most popular method of deforming reduction under
pressure.
• It is based upon analogous behavior to first order reaction where the pores in the
mass are the reactant, i.e.,
Log 1/E=Ky . P+Kr
where,
Ky=material dependent constant but inversely proportional to its yield strength(S)
Kr=related packing stage [E0].
MEHAK AGGARWAL 1/24/2022 17](https://image.slidesharecdn.com/studyofconsolidationparameters-220124173421/85/Study-of-consolidation-parameters-17-320.jpg)