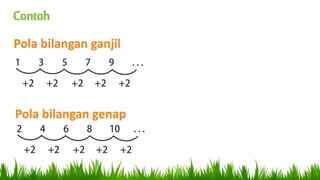
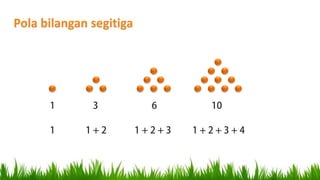
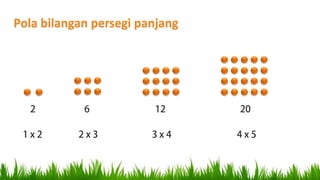
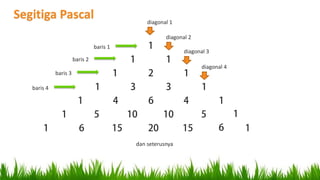
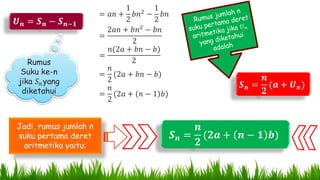
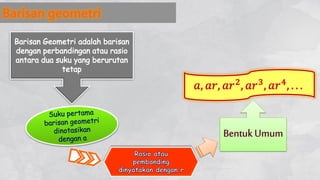
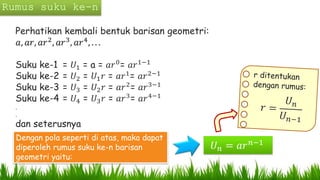
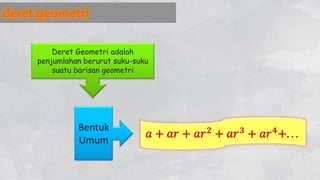
Dokumen ini menjelaskan pola bilangan, termasuk barisan aritmetika dan geometri, serta penggunaannya dalam berbagai konteks seperti produksi, tabungan, dan pertumbuhan penduduk. Ia mencakup rumus untuk menghitung suku, suku tengah, dan jumlah suku, serta memberikan contoh penerapan nyata. Di akhir, terdapat beberapa soal untuk menghitung jumlah kuantitas berdasarkan pola-pola yang telah dijelaskan.

1. Oleh: Emanueli Mendrofa, S.Pd

2. Pola bilangan adalah bilangan-bilangan yang disusun
membentuk aturan tertentu. Misalnya pada kalender
terdapat susunan angka-angka baik mendatar,
menurun, diagonal (miring).

3. Contoh
Pola bilangan ganjil
Pola bilangan genap

4. Pola bilangan segitiga

5. Pola bilangan persegi panjang

6. Segitiga Pascal
dan seterusnya
diagonal 1
diagonal 2
diagonal 3
diagonal 4
baris 1
baris 2
baris 3
baris 4

7. Barisan dan Deret

8. Aturan barisan bilangan ini adalah
tambahkan 2 dari suku sebelumnya

9. deret bilangan ganjil
deret bilangan persegi panjang

10. Saat mengendarai motor, pernahkah
kalian mengamati speedometer pada
motor tersebut? Pada speedometer
terdapat angka-angka 0, 20, 40, 60,
80, 100, dan 120 yang menunjukkan
kecepatan motor saat kalian
mengendarainya. Angka-angka ini
berurutan mulai dari yang terkecil ke
yang terbesar dengan pola tertentu
sehingga membentuk sebuah barisan
aritmetika.

11. Barisan Aritmetika adalah barisan
yang selisih antar dua suku
berurutannya tetap atau sama.
Suku pertama suatu
barisan dinotasikan
dengan a a, a + b, a + 2b, a + 3b, . . .

12. Perhatikan kembali bentuk barisan aritmetika:
a, a + b, a + 2b, a + 3b, . . .
Suku ke-1 = 𝑈1 = a = a + (1 – 1) b
Suku ke-2 = 𝑈2 = a + b = a + (2 – 1) b
Suku ke-3 = 𝑈3 = a + 2b = a + (3 – 1) b
Suku ke-4 = 𝑈4 = a + 3b = a + (4 – 1) b
.
.
dan seterusnya 𝑈 𝑛 = 𝑎 + 𝑛 − 1 𝑏
Dengan pola seperti di atas, maka dapat
diperoleh rumus suku ke-n barisan
aritmetika yaitu:

13. Suku tengah suatu barisan aritmetika adalah suku barisan yang
letaknya di tengah-tengah jika banyak sukunya ganjil. Misal
diberikan barisan aritmetika dengan suku tengah 𝑈 𝑘, sehingga
banyaknya suku (2k – 1), maka barisan itu dapat dituliskan sebagai
a, . . . , 𝑈 𝑘, . . ., 𝑈2𝑘−1.
Berdasarkan rumus ke-n barisan aritmetika, diperoleh:
𝑈 𝑘 = 𝑎 + 𝑘 − 1 𝑏
=
1
2
2𝑎 + 2 𝑘 − 1 𝑏
=
1
2
𝑎 + 𝑎 + 2𝑘 − 2 𝑏 =
1
2
𝑈1 + 𝑈2𝑘−1

14. Jadi, suku tengah barisan aritmetika adalah
𝑈 𝑘 =
1
2
𝑈1 + 𝑈2𝑘−1
Apabila belum diketahui banyak sukunya, yang diketahui hanya suku
terakhir (𝑈 𝑛) maka suku tengah barisan aritmetika ditentukan
dengan:
𝑈 𝑘 =
1
2
𝑈1 + 𝑈 𝑛

15. Misal diberikan dua bilangan x dan y (x ≠ y), kemudian di antara
kedua bilangan tersebut disisipkan k bilangan sehingga membentuk
barisan aritmetika.
𝑥, 𝑥 + 𝑏 , 𝑥 + 2𝑏 , . . . , 𝑥 + 𝑘𝑏 , 𝑦
Maka beda dari barisan aritmetika tersebut dapat ditentukan
sebagai berikut:
Bilangan-bilangan yang disisipkan

16. 𝑦 − 𝑥 + 𝑘𝑏 = 𝑏
𝑦 − 𝑥 − 𝑘𝑏 = 𝑏
𝑦 − 𝑥 = 𝑏 + 𝑘𝑏
𝑘𝑏 + 𝑏 = 𝑦 − 𝑥
𝑘 + 1 𝑏 = 𝑦 − 𝑥
𝑏 =
𝑦 − 𝑥
𝑘 + 1
Jadi, beda barisan aritmetika yang terbentuk adalah:
𝑏 =
𝑦 − 𝑥
𝑘 + 1

17. Diketahui barisan aritmetika 21, 17, 13, . . ., -11. Banyak suku barisan ganjil.
a. Tentukan suku tengahnya.
b. Suku ke berapa suku tengahnya?
Jawab:
Jadi, suku tengahnya 5
Jadi, suku tengahnya suku ke-5
𝑈1 = 21
𝑈 𝑛 = −11
𝑈 𝑘 =
1
2
𝑈1 + 𝑈 𝑛 =
1
2
{21 + (−11)} = 5
a. 𝑈 𝑛 = 𝑎 + 𝑛 − 1 𝑏b.
5 = 21 + 𝑛 − 1 (17 − 21)
5 = 21 + 𝑛 − 1 (−4)
5 = 21 − 4𝑛 + 4
5 − 25 = −4𝑛
−20 = −4𝑛
𝑛 = 5

18. Didalam sebuah gedung teater terdapat kursi yang diatur sebagai berikut. Baris pertama
berisi 15 kursi, baris kedua 20 kursi, baris ketiga 25 kursi, dan seterusnya selisih 5 kursi
dengan barisan yang didepannya.
a. Tentukan banyak kursi pada baris ke-6.
b. Baris ke berapa yang terisi 60 kursi?
Jawab:
Aturan penempatan kursi membentuk barisan aritmetika dengan a = 15 dan b = 5.
a.
Jadi, banyak kursi pada baris ke-6 adalah 40
𝑈 𝑛 = 𝑎 + 𝑛 − 1 𝑏
𝑈6 = 15 + 6 − 1 5 = 15 + 5 . 5 = 15 + 25 = 40

19. b.
Jadi, baris yang berisi 60 kursi adalah baris ke-10
𝑈 𝑛 = 60
𝑈 𝑛 = 𝑎 + 𝑛 − 1 𝑏
60 = 15 + 𝑛 − 1 5
60 = 15 + 5𝑛 − 5
60 = 10 + 5𝑛
60 − 10 = 5𝑛
50 = 5𝑛
𝑛 = 10

20. Carl Friedrick Gauss,
menentukan jumlah bilangan 1 –
100 dengan cara membalikkan
bilangan tersebut kemudian
menjumlahkannya. Hasil
penjumlahannya dikalikan dengan
banyak bilangan lalu dibagi
dengan 2.

21. Bentuk umum
deret
aritmetika
a + (a + b) + (a + 2b) + (a + 3b) + . . . + (a + (n – 1)b)

22. Jumlah n suku pertama deret aritmetika dinyatakan dengan 𝑆 𝑛.
Dengan notasi sigma 𝑆 𝑛 dapat ditulis sebagai:
𝑆 𝑛 =
𝑘=1
𝑛
(𝑎 + 𝑘 − 1 𝑏)
Selanjutnya, akan dicari bentuk umum dengan menggunakan kaidah-
kaidah notasi sigma.

23. 𝑆 𝑛 =
𝑘=1
𝑛
𝑎 + 𝑘 − 1 𝑏 =
𝑘=1
𝑛
𝑎 + 𝑘𝑏 − 𝑏
=
𝑘=1
𝑛
𝑎 +
𝑘=1
𝑛
𝑘𝑏 −
𝑘=1
𝑛
𝑏
= 𝑎𝑛 + 𝑏
𝑘=1
𝑛
𝑘 − 𝑏𝑛
= 𝑎𝑛 + 𝑏(
𝑛2
+ 𝑛
2
) − 𝑏𝑛
= 𝑎𝑛 +
1
2
𝑏𝑛2
+
1
2
𝑏𝑛 − 𝑏𝑛
= 𝑎𝑛 +
1
2
𝑏𝑛2 +
1
2
𝑏𝑛 − 𝑏𝑛

24. = 𝑎𝑛 +
1
2
𝑏𝑛2
−
1
2
𝑏𝑛
=
2𝑎𝑛 + 𝑏𝑛2 − 𝑏𝑛
2
=
𝑛(2𝑎 + 𝑏𝑛 − 𝑏)
2
=
𝑛
2
(2𝑎 + 𝑏𝑛 − 𝑏)
=
𝑛
2
(2𝑎 + 𝑛 − 1 𝑏)
𝑺 𝒏 =
𝒏
𝟐
(𝟐𝒂 + 𝒏 − 𝟏 𝒃)
Jadi, rumus jumlah n
suku pertama deret
aritmetika yaitu:
𝑺 𝒏 =
𝒏
𝟐
(𝒂 + 𝑼 𝒏)
𝑼 𝒏 = 𝑺 𝒏 − 𝑺 𝒏−𝟏
Rumus
Suku ke-n
jika 𝑆 𝑛yang
diketahui

25. Hitunglah jumlah 10 suku pertama deret aritmetika 2 + 4 + 6 + ...
Jawab:
Suku pertama : a = 2
Beda : b = 4 – 2 = 2
n = 10
𝑆 𝑛 =
𝑛
2
(2𝑎 + 𝑛 − 1 𝑏)
𝑆10 =
10
2
(2 . 2 + 10 − 1 2)
𝑆10 = 5 (4 + 9 . 2)
𝑆10 = 5 (4 + 18)
𝑆10 = 5 22 = 110

26. Diketahui 𝑈 𝑛 = 5 − 3𝑛, hitunglah 𝑆20.
Jawab:
𝑈1 = a = 5 – 3 . 1 = 5 – 3 = 2
𝑈2 = 5 – 3 . 2 = 5 – 6 = –1
b = 𝑈2 − 𝑈1 = – 1 – 2 = – 3
𝑆 𝑛 =
𝑛
2
(2𝑎 + 𝑛 − 1 𝑏)
𝑆20 =
20
2
2 . 2 + 20 − 1 − 3 = 10 4 + 19 . −3 = 10(4 − 57)
𝑆20 = 10 −53 = −530

27. Sebuah usaha konveksi memproduksi seragam siswa
SMA. Pada awal produksi menghasilkan 200 potong.
Atas permintaan pasar, produksi bertambah 50 potong
setiap bulannya. Jika produksi dimulai pada bulan Mei
2014, berapa jumlah produksi sampai dengan bulan
April 2015?

28. Seorang pegawai menabung pada sebuah bank. Tahun
pertama, setiap bulannya ia menabung Rp100.000,00.
Tahun kedua, setiap bulannya ia menabung
Rp125.000,00. Tahun ketiga, setiap bulannya ia
menabung Rp150.000, dan seterusnya setiap tahun
bertambah Rp25.000,00 per bulannya. Berapa jumlah
uang pegawai itu setelah ditabungnya 15 tahun (bunga
yang di bank tidak ikut diperhitungkan)?

29. Jumlah seragam yang diproduksi setiap bulan membentuk barisan aritmetika
dengan a = 200 dan b = 50.
𝑈1 = produksi pada bulan Mei 2014 = 200
𝑈2 = produksi pada bulan Juni 2014 = 250
.
.
.
𝑈12 = produksi pada bulan April 2015
Jumlah produksi sampai dengan April 2015 = 𝑆12
Jadi, jumlah produksi sampai dengan April 2015 sebanyak 5.700 potong.
𝑆 𝑛 =
𝑛
2
(2𝑎 + 𝑛 − 1 𝑏)
𝑆12 =
12
2
2 . 200 + 12 − 1 50 = 6 400 + 11 . 50 = 6 400 + 550 = 5.700

30. Tabungan perbulan pada tahun pertama = Rp100.000,00
Tabungan perbulan pada tahun kedua = Rp125.000,00
Tahun berikutnya bertambah Rp25.000 perbulan
Jadi,
𝑈1 = tabungan pada tahun pertama = Rp100.000 x 12 = Rp1.200.000,00
𝑈2 = tabungan pada tahun kedua = Rp125.000 x 12 = Rp1.500.000,00
𝑈3 = tabungan pada tahun ketiga = Rp150.000 x 12 = Rp1.800.000,00
.
.
.
𝑈15 = tabungan pada tahun kelima belas

31. Beda = Rp1.800.000,00 − Rp1.500.000,00 = Rp300.000,00
Jumlah tabungan sampai pada tahun kelima belas = 𝑆15
𝑆 𝑛 =
𝑛
2
(2𝑎 + 𝑛 − 1 𝑏)
𝑆15 =
15
2
2 × 1.200.000 + 15 − 1 300.000
𝑆15 =
15
2
2.400.000 + 14 × 300.000
𝑆15 =
15
2
2.400.000 + 4.200.000
𝑆15 =
15
2
6.600.000
𝑆15 =
99.000.000
2
= 49.500.000
Jadi, jumlah uang
pegawai itu setelah
ditabungnya 15 tahun
adalah Rp49.500.000,00

32. Perhatikan masalah berikut!
Dalam menghadapi suatu situasi tertentu
komandan teritorial memberikan perintah
kepada 15 orang komandan sektor, yang masing-
masing meneruskan lagi kepada 15 orang
komandan pasukan. Tiap-tiap komandan pasukan
juga meneruskan kepada 15 orang komandan
regu. Tiap komandan regu meneruskan kepada
anggota regunya yang jumlahnya masing-masing
juga 15 orang. Berapakah orangkah yang
mengetahui tentang perintah itu?
Permasalahan tersebut dapat disusun menjadi
suatu barisan bilangan berikut:
1, 1(15), 1(15)(15), 1(15)(15)(15),
1(15)(15)(15)(15), . . .

34. Perhatikan kembali bentuk barisan geometri:
𝑎, 𝑎𝑟, 𝑎𝑟2, 𝑎𝑟3, 𝑎𝑟4, . . .
Suku ke-1 = 𝑈1 = a = 𝑎𝑟0= 𝑎𝑟1−1
Suku ke-2 = 𝑈2 = 𝑈1 𝑟 = 𝑎𝑟1= 𝑎𝑟2−1
Suku ke-3 = 𝑈3 = 𝑈2 𝑟 = 𝑎𝑟2= 𝑎𝑟3−1
Suku ke-4 = 𝑈4 = 𝑈3 𝑟 = 𝑎𝑟3= 𝑎𝑟4−1
.
.
dan seterusnya
𝑈 𝑛 = 𝑎𝑟 𝑛−1
Dengan pola seperti di atas, maka dapat
diperoleh rumus suku ke-n barisan
geometri yaitu:

35. Diketahui suatu barisan geometri dengan a = 1 dan 𝑈7 = 64. Tentukan 𝑈10.
Jawab:
a = 1
𝑈7 = 𝑎𝑟6  64 = 𝑎𝑟6
64 = 1 . 𝑟6
𝑟6
= 64
𝑟 =
6
64 =
6
26 = 2
Suku ke-10 = 𝑈10 = 𝑎𝑟9= 1 . 29 = 512
Jadi, suku ke-10 barisan tersebut adalah 512.

36. Pada awal tahun, penduduk suatu kota adalah 15.000 orang. Setiap awal tahun, jumlah
penduduk kota tersebut tetap dihitung. Karena kelahiran dan urbanisasi penduduk, setiap
tahunnya jumlah penduduk bertambah 5% dari tahun sebelumnya. Tentukan jumlah
penduduk pada awal tahun ke-10!
Jawab:
Penduduk pada awal tahun pertama adalah 𝑈1 = a = 15.000
Pada awal tahun ke-2 adalah:
𝑈2 = 15.000 + 5% . 15.000
𝑈2 = 15.000 +
5
100
. 15.000
𝑈2 = 15.000 (1 +
5
100
)

37. Pada awal tahun ke-3 adalah:
𝑈3 = 𝑈2 + 5% . 𝑈2
𝑈3 = 𝑈2(1 +
5
100
)
𝑈3 = 15.000 (1 +
5
100
)(1 +
5
100
)
𝑈3 = 15.000 (1 +
5
100
)2
Jika proses ini dilanjutkan maka akan diperoleh:
𝑈 𝑛 = 15.000 (1 +
5
100
) 𝑛−1

38. Dengan demikian jumlah penduduk pada awal tahun ke-10 adalah:
𝑈10 = 15.000 (1 +
5
100
)10−1
𝑈10 = 15.000 (1 +
5
100
)9
𝑈10 = 15.000 (
100 + 5
100
)9
𝑈10 = 15.000 (
105
100
)9
𝑈10 = 15.000 (1,05)9
𝑈10 = 15.000 × 1,55132821597852
𝑈10 = 23.270
Jadi, jumlah penduduk pada awal tahun ke-10 adalah 23.270 orang

39. Suku tengah suatu barisan geometri adalah suku barisan yang
letaknya di tengah-tengah jika banyak sukunya ganjil. Misal barisan
geometri dengan suku tengah 𝑈 𝑘, sehingga banyaknya suku (2k – 1),
maka barisan itu dapat dituliskan sebagai 𝑈1, . . . , 𝑈 𝑘, . . ., 𝑈2𝑘−1.
Suku tengah barisan geometri ditentukan dengan rumus:
𝑈 𝑘 = 𝑈1 × 𝑈 𝑛

40. Misal diberikan dua bilangan x dan y (x ≠ y), kemudian di antara
kedua bilangan tersebut disisipkan k bilangan sehingga membentuk
barisan geometri.
𝑥, 𝑥𝑟, 𝑥𝑟2, 𝑥𝑟3, . . . , 𝑥𝑟 𝑘, 𝑦
Maka rasio r dari barisan geometri tersebut dapat ditentukan
sebagai berikut:
Bilangan-bilangan yang disisipkan

41. 𝑦
𝑥𝑟 𝑘
= 𝑟
𝑦
𝑥
= 𝑟 . 𝑟 𝑘
𝑟 𝑘+1 =
𝑦
𝑥
𝑟 =
𝑘+1 𝑦
𝑥
=
𝑦
𝑥
1
𝑘+1
Jadi, rasio barisan geometri yang terbentuk adalah:
𝑟 =
𝑘+1 𝑦
𝑥
=
𝑦
𝑥
1
𝑘+1

42. Deret Geometri adalah
penjumlahan berurut suku-suku
suatu barisan geometri
Bentuk
Umum

43. Jumlah n suku pertama deret geometri dinyatakan dengan 𝑆 𝑛,
ditentukan dengan rumus:
𝑆 𝑛 =
𝑎(1 − 𝑟 𝑛
)
1 − 𝑟
atau
𝑆 𝑛 =
𝑎(𝑟 𝑛 − 1)
𝑟 − 1
Untuk r < 1
Untuk r > 1

44. Diketahui deret geometri 2 + 1 +
1
2
+
1
4
+ . . . Tentukan
a. rasio
b. suku ke-10
c. jumlah 10 suku pertama
Jawab:
a. Rasio
𝑟 =
𝑈 𝑛
𝑈 𝑛−1
=
𝑈2
𝑈1
=
1
2

45. b. suku ke-10
𝑈 𝑛 = 𝑎𝑟 𝑛−1
𝑈10 = 𝑎𝑟10−1
𝑈10 = 2 .
1
2
9
𝑈10 = 2 .
1
512
𝑈10 =
1
256
c. Jumlah 10 suku pertama
𝑆 𝑛 =
𝑎(1 − 𝑟 𝑛)
1 − 𝑟
𝑆10 =
2 1 −
1
2
10
1 −
1
2
=
2 1 −
1
1.024
1
2
𝑆10 = 2
1.023
1.024
× 2 =
2.046
1.024
× 2
𝑆10 = 3,996

46. Dalam suatu n suku deret geometri, 𝑈1 + 𝑈2 = 4, 𝑈 𝑛−1 + 𝑈 𝑛 = 108 dan 𝑆 𝑛 = 121.
Tentukan nilai n, a, dan r.
Jawab:
𝑈1 + 𝑈2 = 4  𝑎 + 𝑎𝑟 = 4
 𝑎(1 + 𝑟) = 4
 𝑎 =
4
1+𝑟
..... (i)
𝑈 𝑛−1 + 𝑈 𝑛 = 108  𝑎𝑟 𝑛−2 + 𝑎𝑟 𝑛−1 = 108
 𝑎𝑟 𝑛−2 1 + r = 108 ..... (ii)

47. Substitusi persamaan (i) ke persamaan (ii)
𝑎𝑟 𝑛−2 1 + r = 108 
4
1+𝑟
𝑟 𝑛−2 1 + r = 108

4𝑟 𝑛−2(1+𝑟)
1+𝑟
= 108
 4𝑟 𝑛−2
= 108
 𝑟 𝑛−2 = 27
 𝑟 𝑛 = 27𝑟2 ...... (iii)

48. Substitusi persamaan (i) dan persamaan (iii) ke rumus 𝑆 𝑛.
𝑆 𝑛 =
𝑎(𝑟 𝑛 − 1)
𝑟 − 1
121 =
4
1 + 𝑟
(27𝑟2
− 1)
𝑟 − 1
121 =
108𝑟2
− 4
1 + 𝑟
𝑟 − 1
121𝑟 − 121 =
108𝑟2
− 4
1 + 𝑟
121𝑟 − 121 1 + 𝑟 = 108𝑟2
− 4
121𝑟2 − 121 = 108𝑟2 − 4

49. 121𝑟2 − 121 + 4 = 108𝑟2
121𝑟2
− 117 = 108𝑟2
121𝑟2
= 108𝑟2
+ 117
121𝑟2 − 108𝑟2 = 117
13𝑟2 = 117
𝑟2
=
117
13
𝑟2 = 9
𝑟 = 3
Karena 𝑟 𝑛 = 27𝑟2, maka:
𝑟 𝑛
= 27 3 2
𝑟 𝑛 = 3 3 3 2
𝑟 𝑛 = 3 5

50. Nilai a adalah:
𝑎 =
4
1 + 𝑟
=
4
1 + 3
= 1
Jadi, a = 1, r = 3 dan n = 5.

51. Seutas tali dipotong menjadi 6 bagian. Panjang keenam
potong tali itu membentuk suatu deret geometri. Jika
panjang potongan tali yang terpendek 3 cm dan
terpanjang 96 cm, tentukan panjang tali semula.

52. Suatu jenis mobil mengalami depresiasi (penurunan
harga jual) sebesar 15% pada setiap akhir tahun. Jika
harga mobil baru Rp150.000.000,00, berapakah harga
jual mobil tersebut pada akhir tahun ke-6?

53. 𝑈1 = 𝑎 = 3
𝑛 = 6
𝑈6 = 𝑎𝑟5 = 96  3 . 𝑟5 = 96
 𝑟5 =
96
3
 𝑟5 = 32
 𝑟 =
5
32 = 2
𝑆 𝑛 =
𝑎(𝑟 𝑛
− 1)
𝑟 − 1
𝑆6 =
3(26
− 1)
2 − 1
=
3(64 − 1)
2 − 1
=
3 × 63
1
= 189
Jadi, panjang tali semula adalah 189 cm

54. 𝑈6 = 150.000.000 (1 −
15
100
)6−1
𝑈6 = 150.000.000 (1 −
15
100
)5
𝑈6 = 150.000.000(
100 − 15
100
)5
𝑈6 = 150.000.000(
85
100
)5
𝑈6 = 150.000.000(0,85)5
𝑈6 = 150.000.000 × 0,4437053125
𝑈6 = 66.555.797
Jadi, harga jual mobil tersebut pada akhir tahun ke-6 adalah Rp66.555.797,00