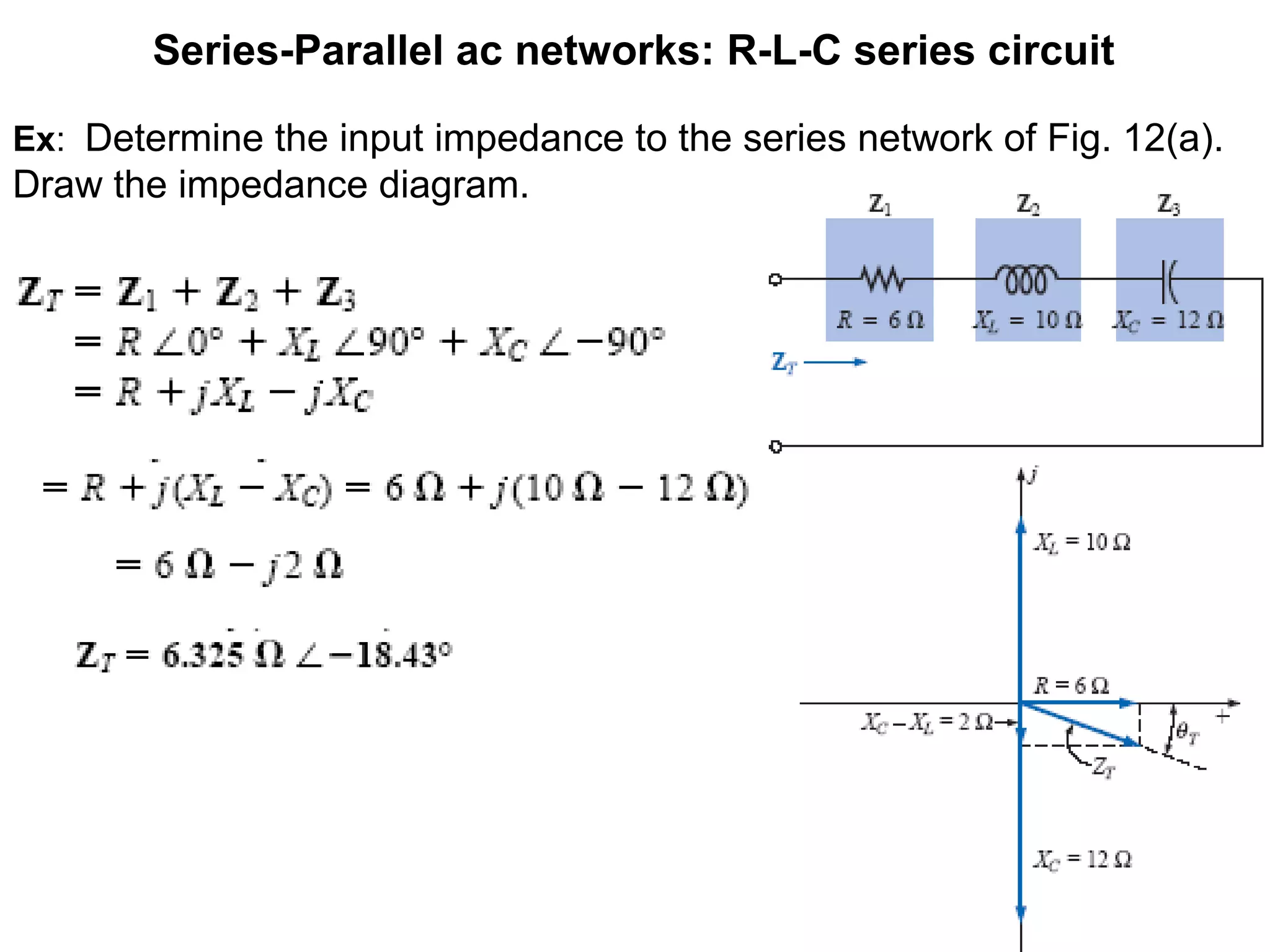
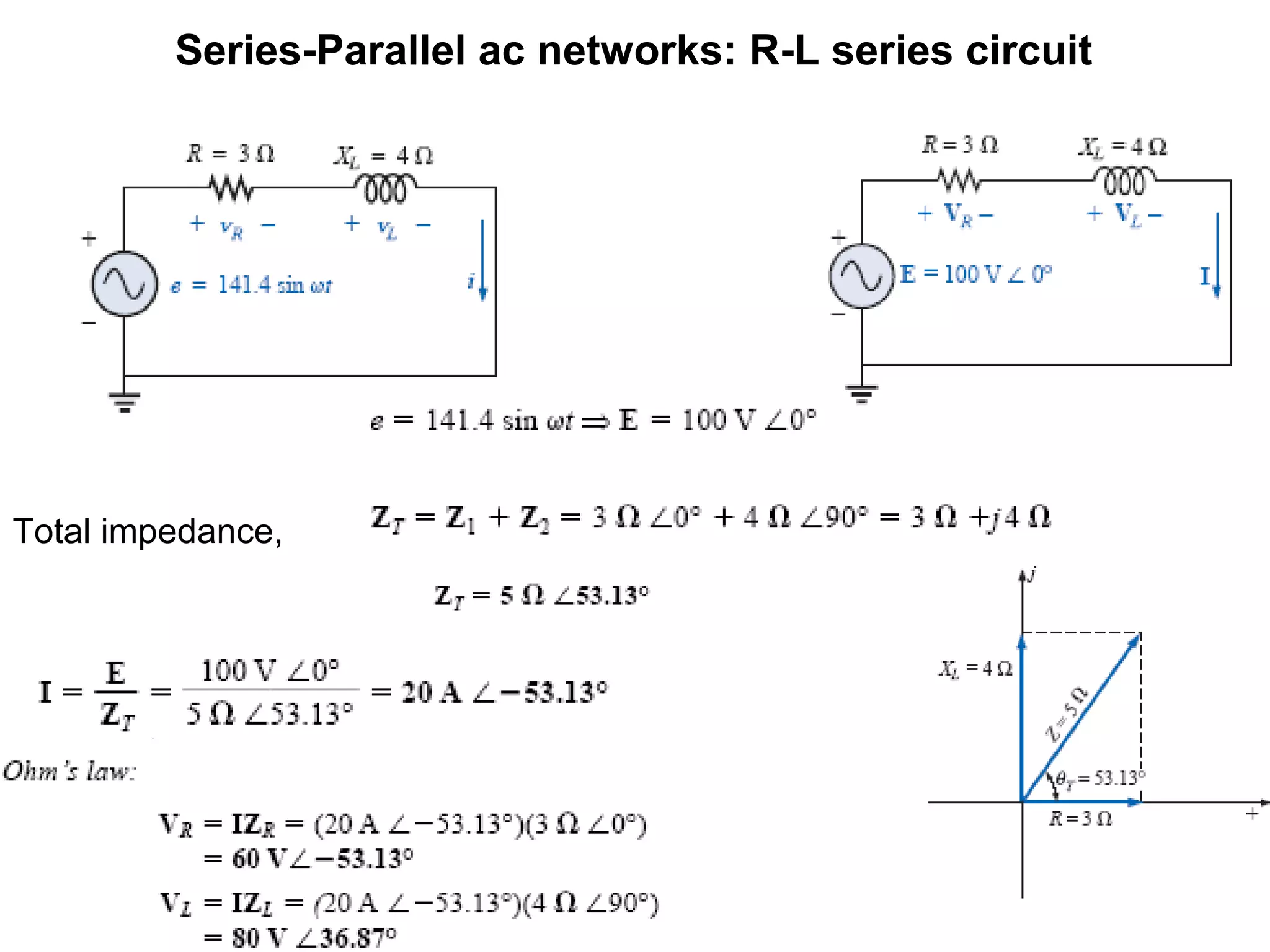
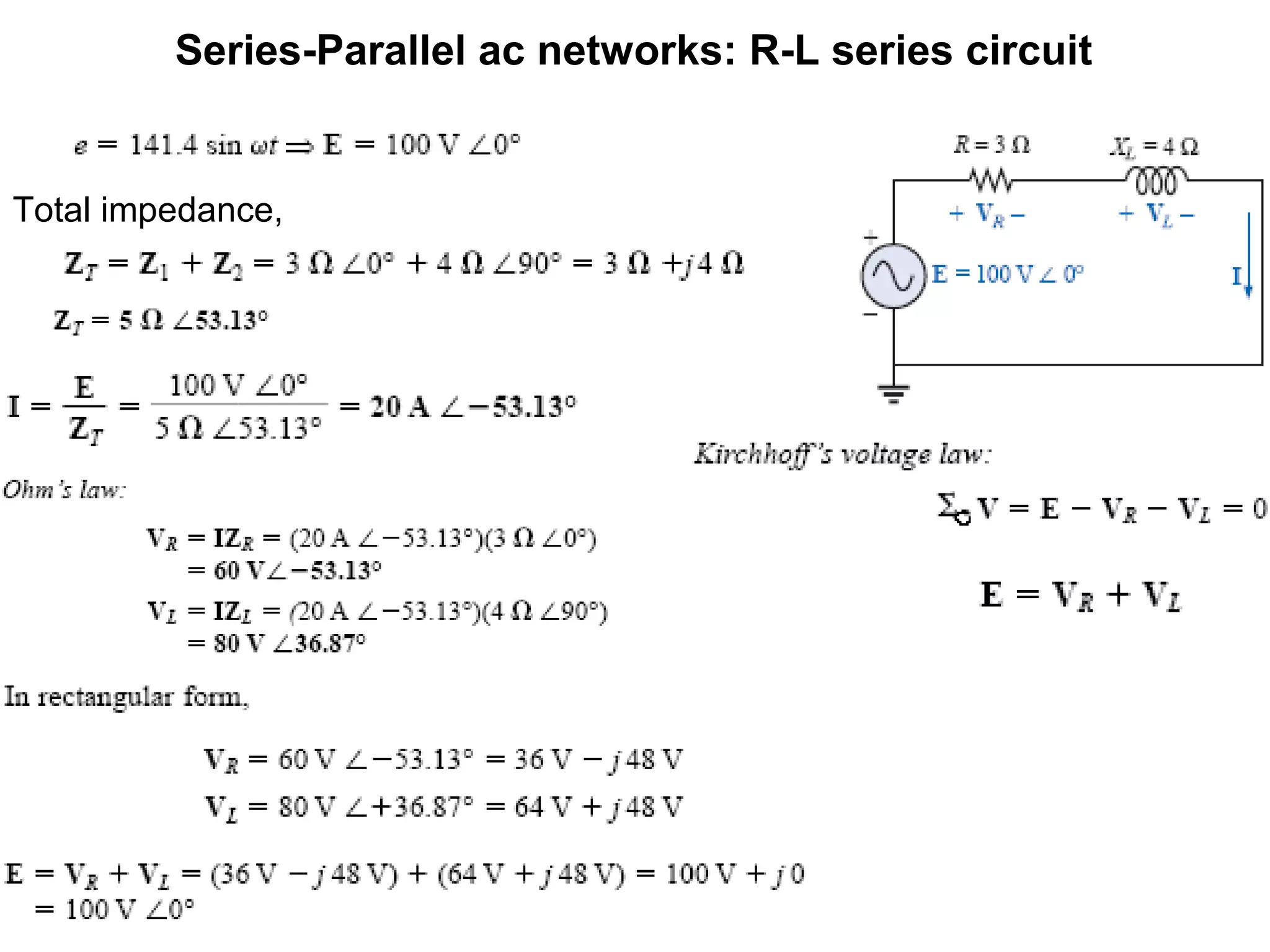
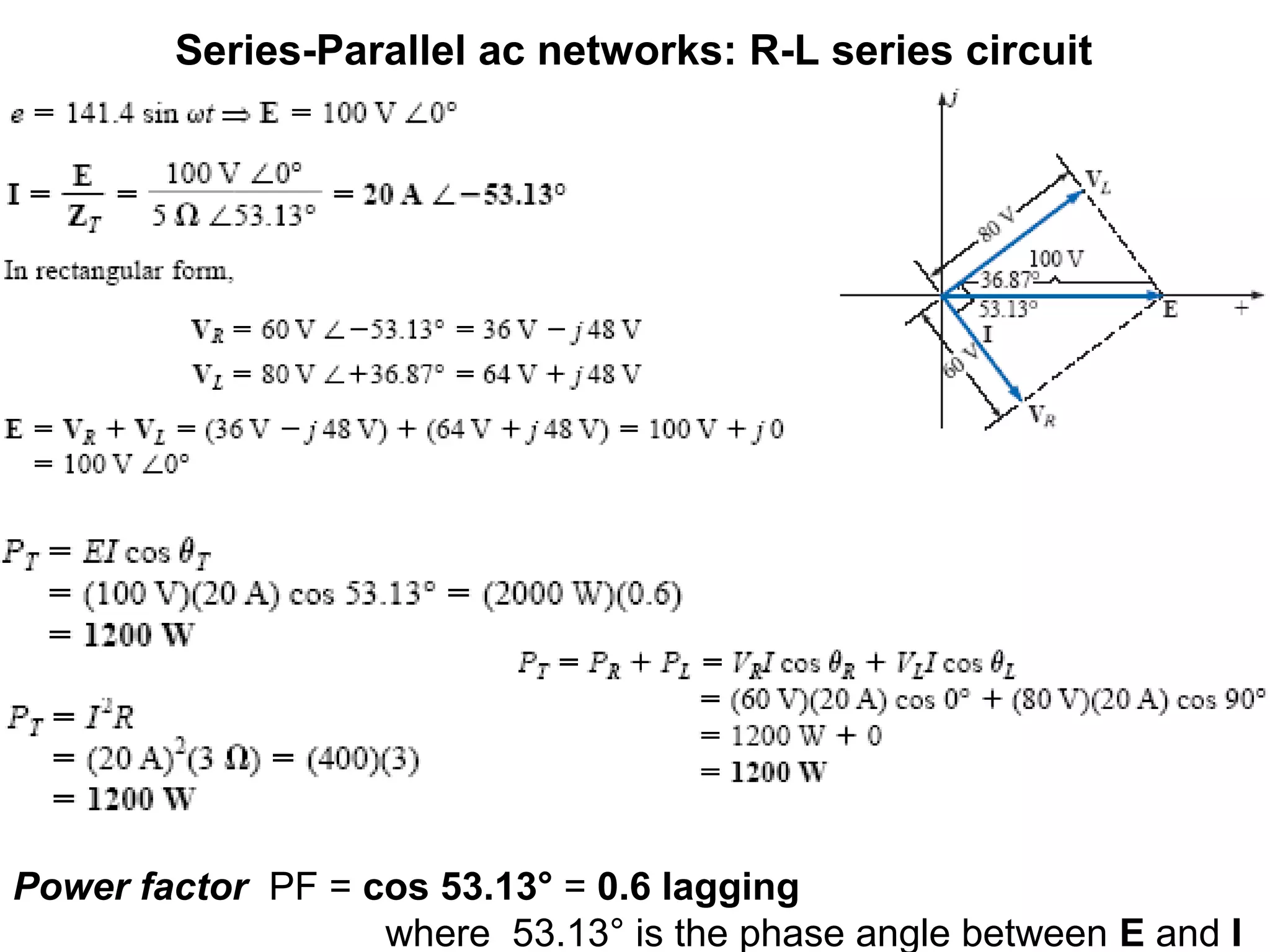
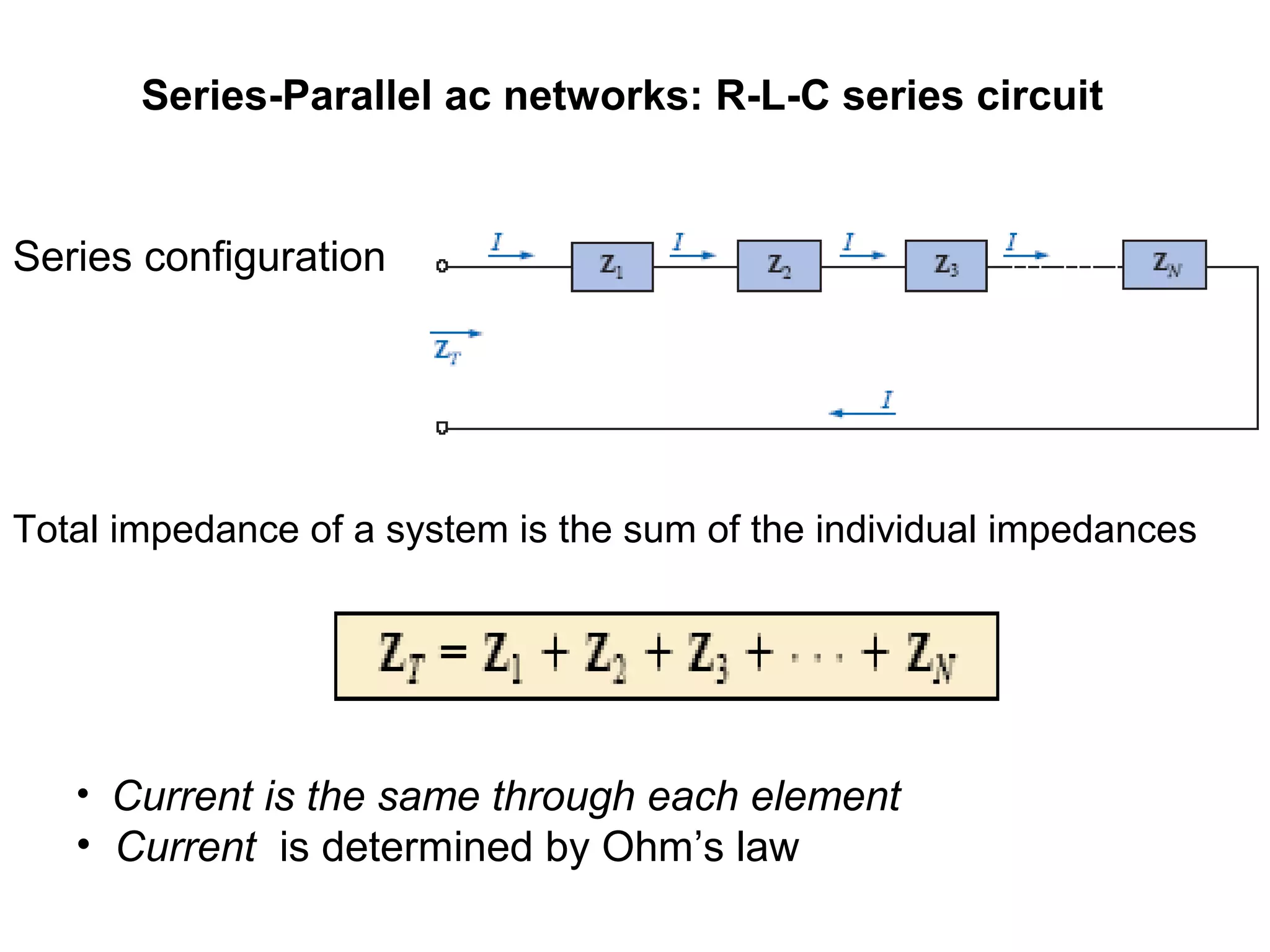
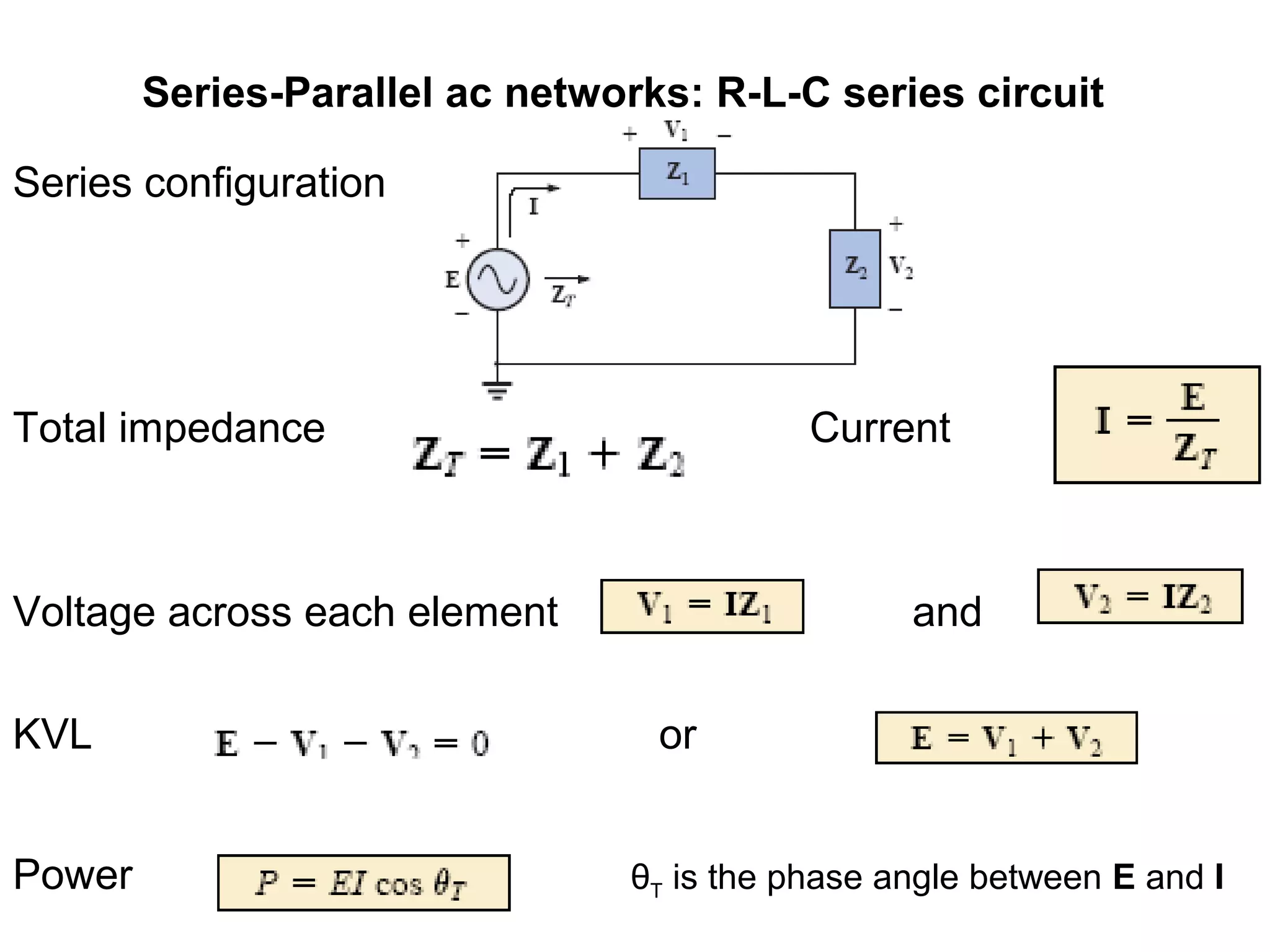
The document explains series-parallel AC networks focusing on R-L-C series circuits, detailing how current and impedance are calculated according to Ohm's law. It outlines the formulas for total impedance and phase angles for R-L, R-C, and R-L-C configurations. Additionally, it provides examples for determining input impedance and calculating power factor.

1. Series-Parallel
ac networks
R-L-C series
circuit

2. Series-Parallel ac networks: R-L-C series circuit
Series configuration
• Current is the same through each element
• Current is determined by Ohm’s law
Total impedance of a system is the sum of the individual impedances

3. Series-Parallel ac networks: R-L-C series circuit
Series configuration
Total impedance Current
Voltage across each element and
KVL or
Power θT is the phase angle between E and I

4. Series-Parallel ac networks: R-L series circuit
Resistance and Inductance (R-L) in series,
Z1 = R and Z2 = j XL = j ωL
Then, ZT = R + j XL = R + j ωL
So, the magnitude of the total impedance, ZT = √(R2
+ XL
2
)
and the phase angle, θT = tan-1 (XL/R)
Therefore, (Impedance)2
= (Resistance)2
+ (Reactance)2
and tan (θT) = (Reactance) / (Resistance)

5. Series-Parallel ac networks: R-C series circuit
For a series resistance and capacitance (R-C) circuit,
Z1 = R and Z2 = 1/(jXC) = -j/ωC
Then, ZT = R - j XC = R - j /ωC
So, the magnitude of the total impedance, ZT = √(R2
+ XC
2
)
and the phase angle, θT = tan-1 (-XC/R)
Therefore, (Impedance)2
= (Resistance)2
+ (Reactance)2
and tan (θT) = (- Reactance) / (Resistance)

6. Series-Parallel ac networks: R-L-C series circuit
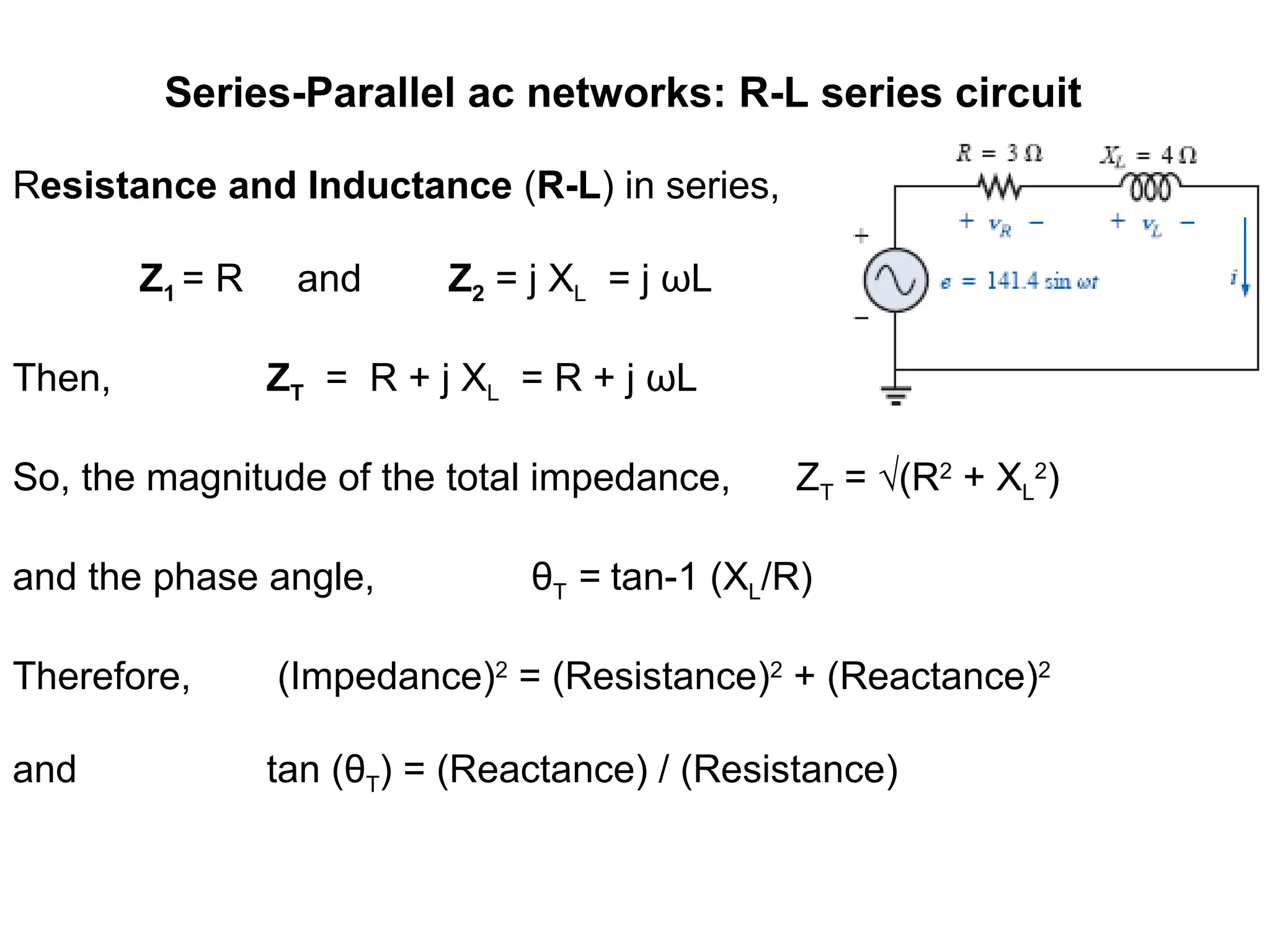
Series resistance, inductance and capacitance (R-L-C) circuit,
Z1 = R, Z2 = j XL = j ωL and Z3 = 1/(jXC)
= -j/ωC
Then, ZT = R + j XL - j XC = R + j ωL - j /ωC
= R + j (XL - XC) = R + j (ωL - 1/ωC)
So, the magnitude of the total impedance, ZT = √(R2
+ (XL -
XC)2
and the phase angle, θT = tan-1 [(XL – XC)/R]
Therefore, (Impedance)2
= (Resistance)2
+ (Total Reactance)2

7. Series-Parallel ac networks: R-L-C series circuit
Ex: Determine the input impedance to the series network of Fig. 12(a).
Draw the impedance diagram.

8. Series-Parallel ac networks: R-L series circuit
Total impedance,
,

9. Series-Parallel ac networks: R-L series circuit
Total impedance,
,

10. Series-Parallel ac networks: R-L series circuit
,
Power factor PF = cos 53.13° = 0.6 lagging
where 53.13° is the phase angle between E and I