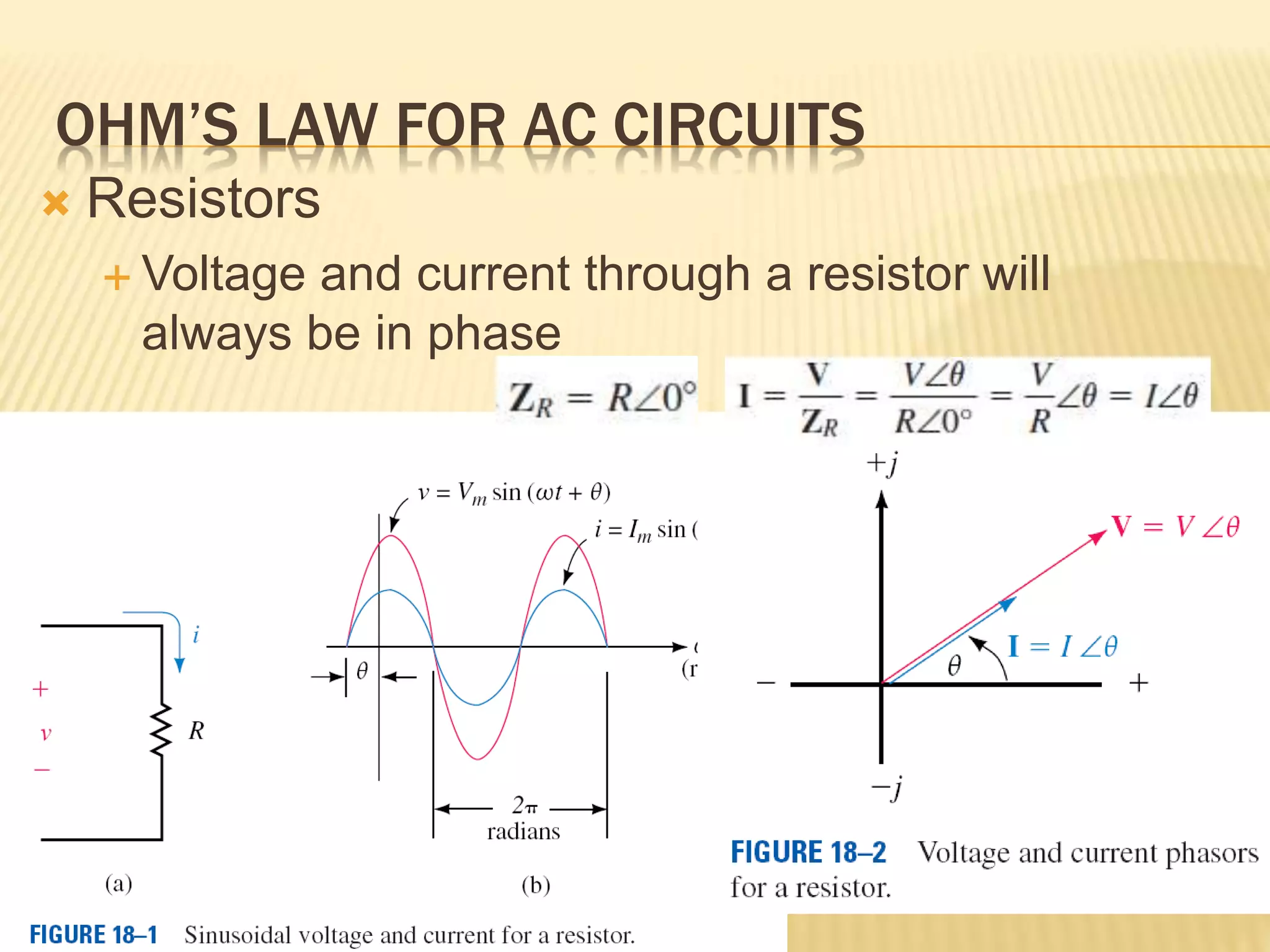
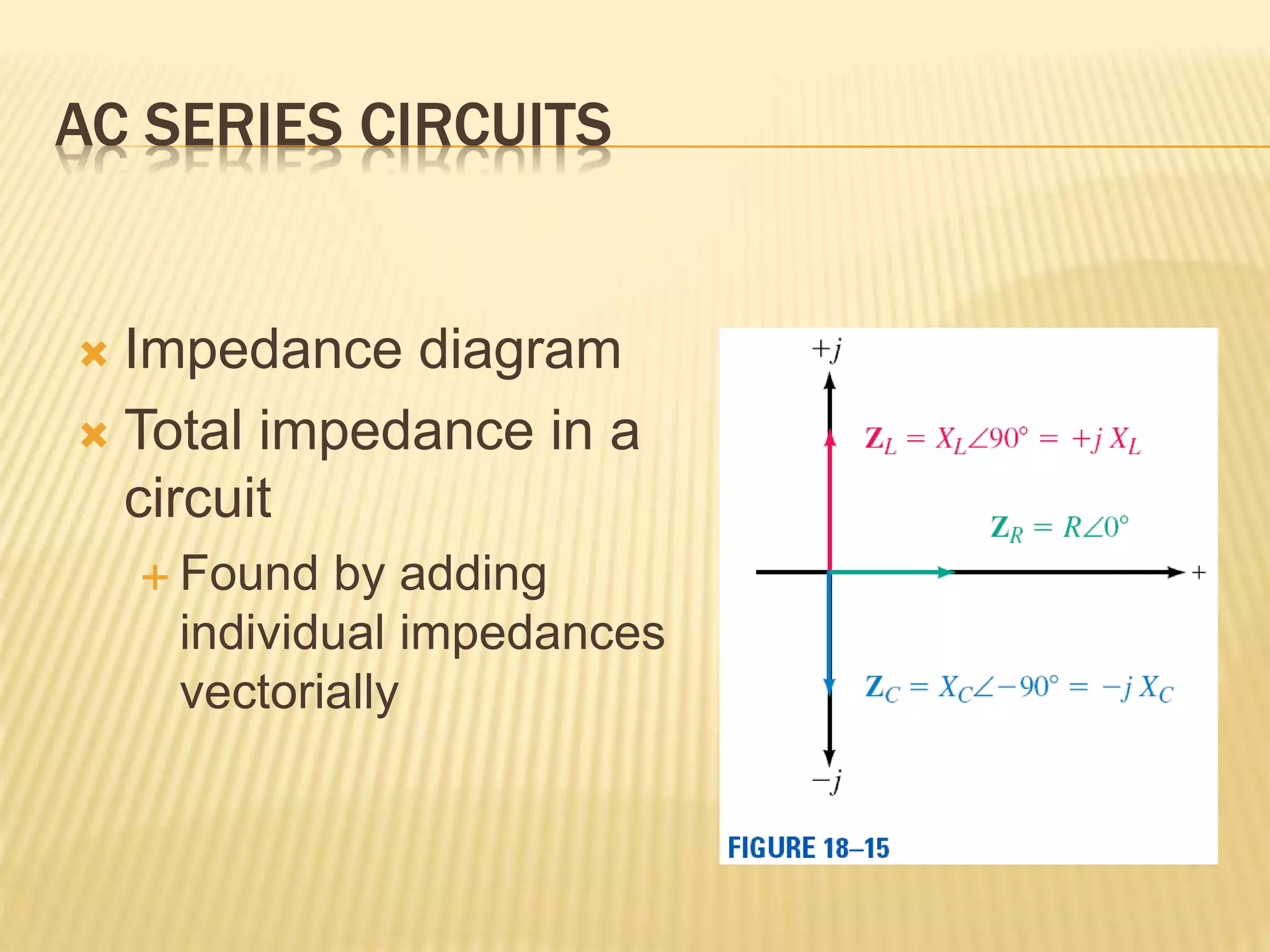
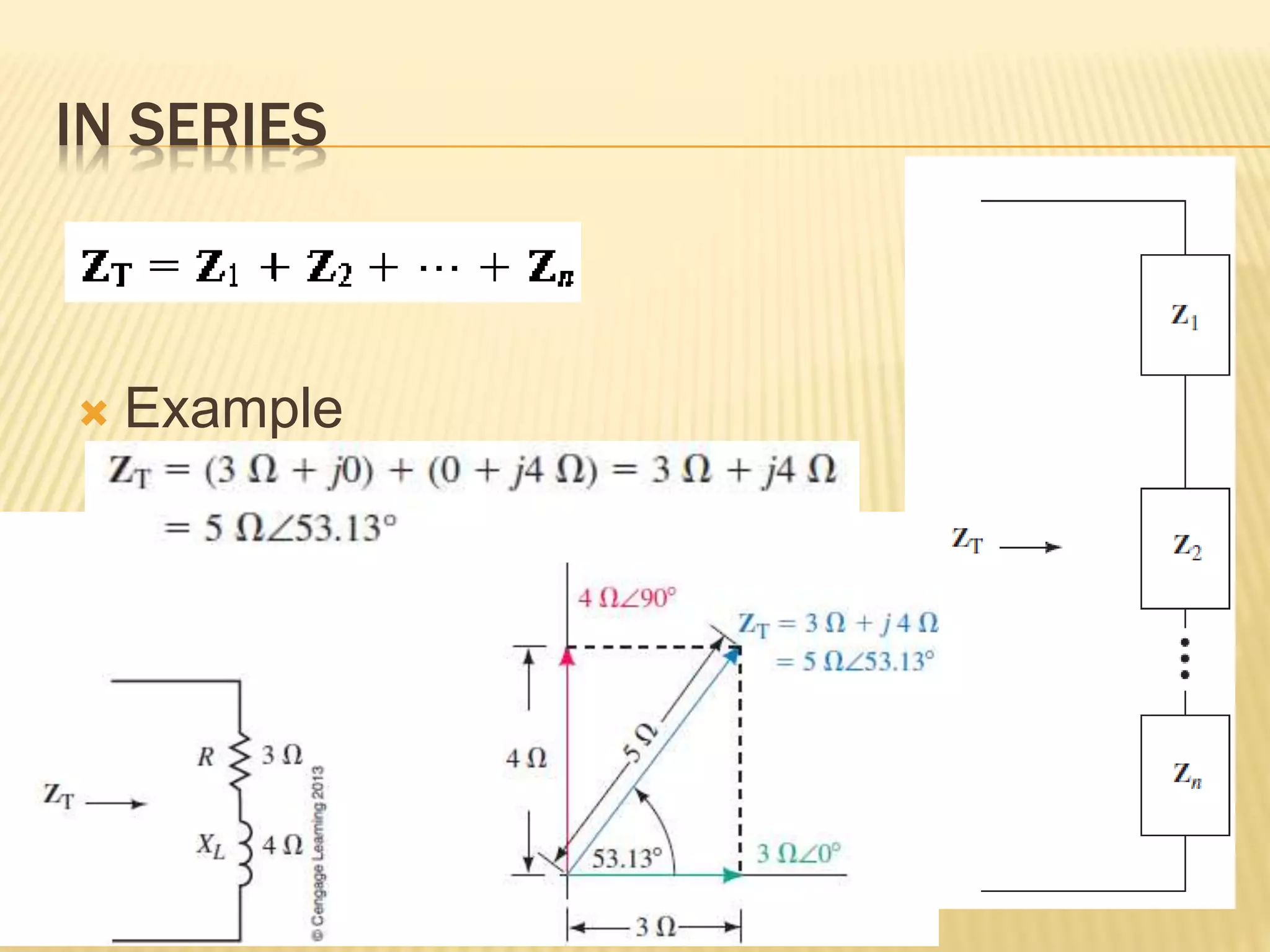
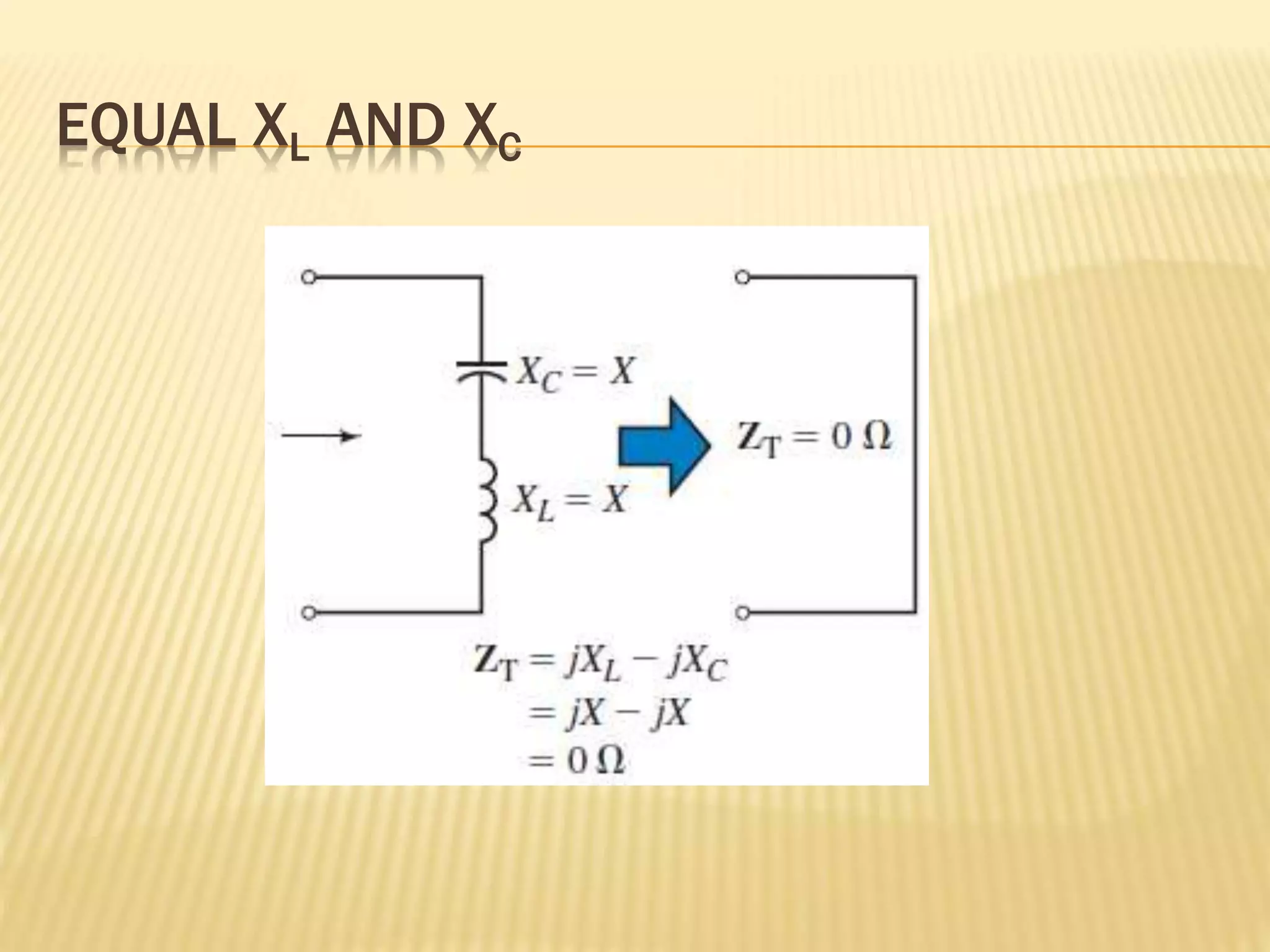
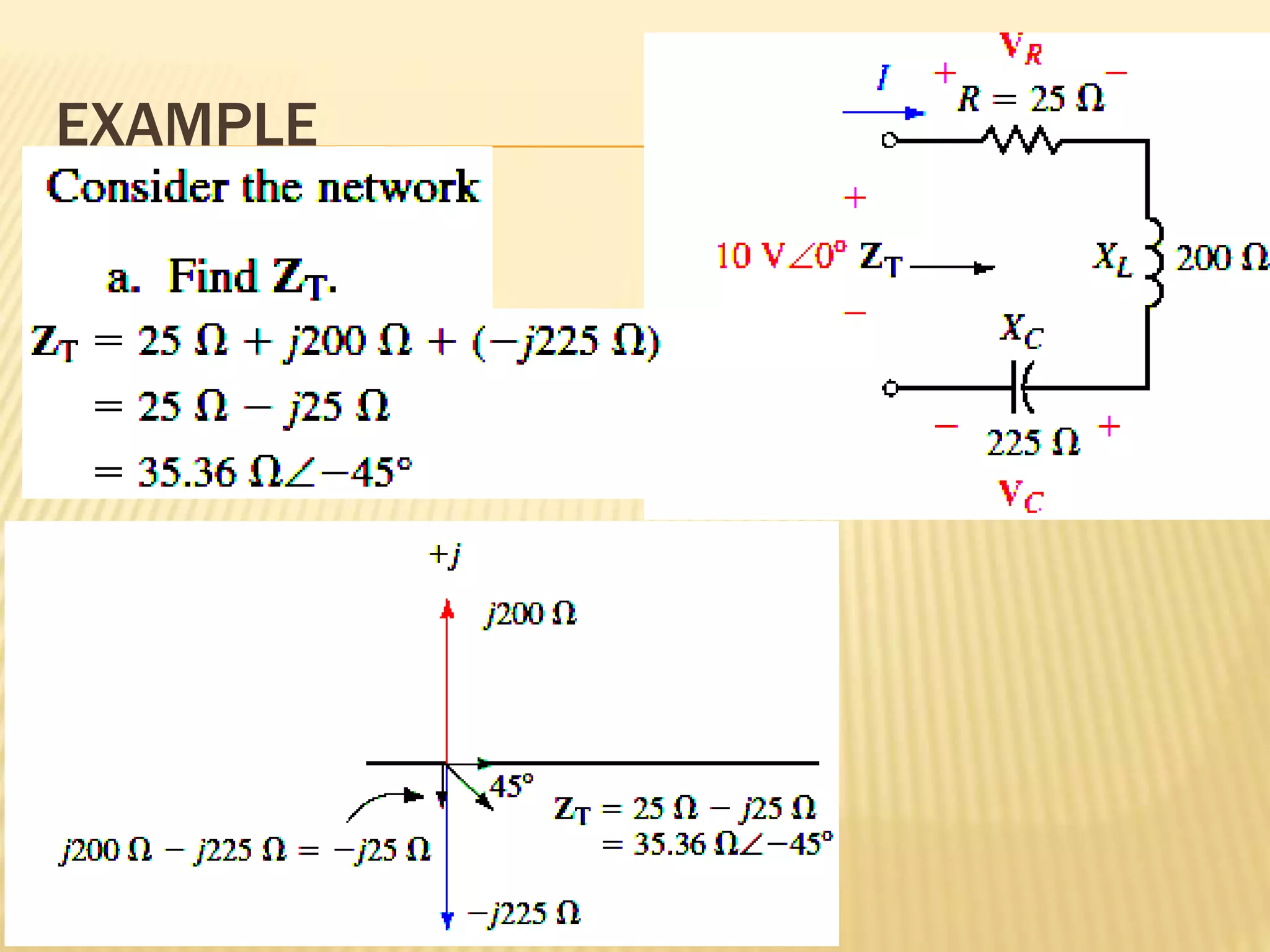
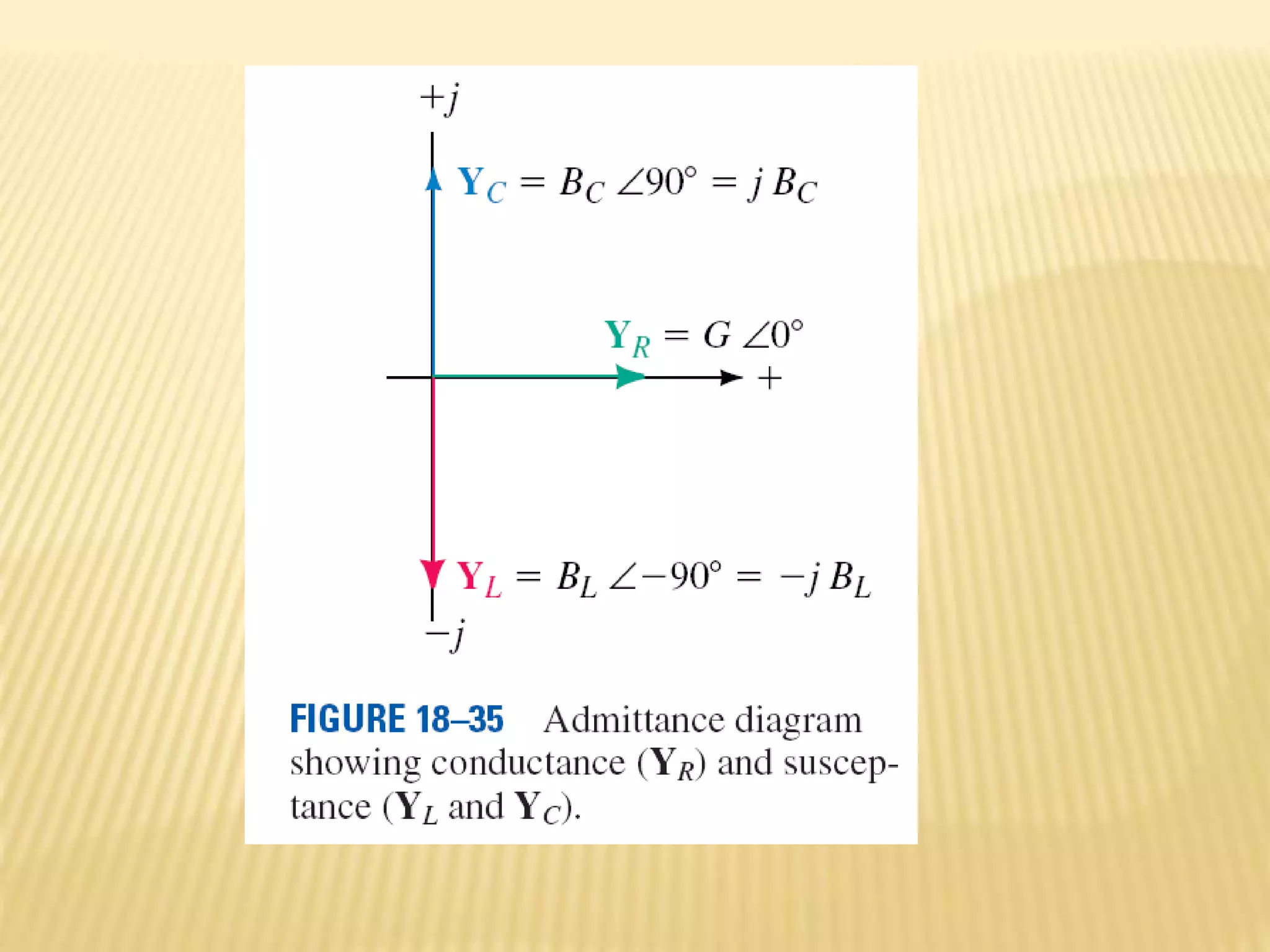
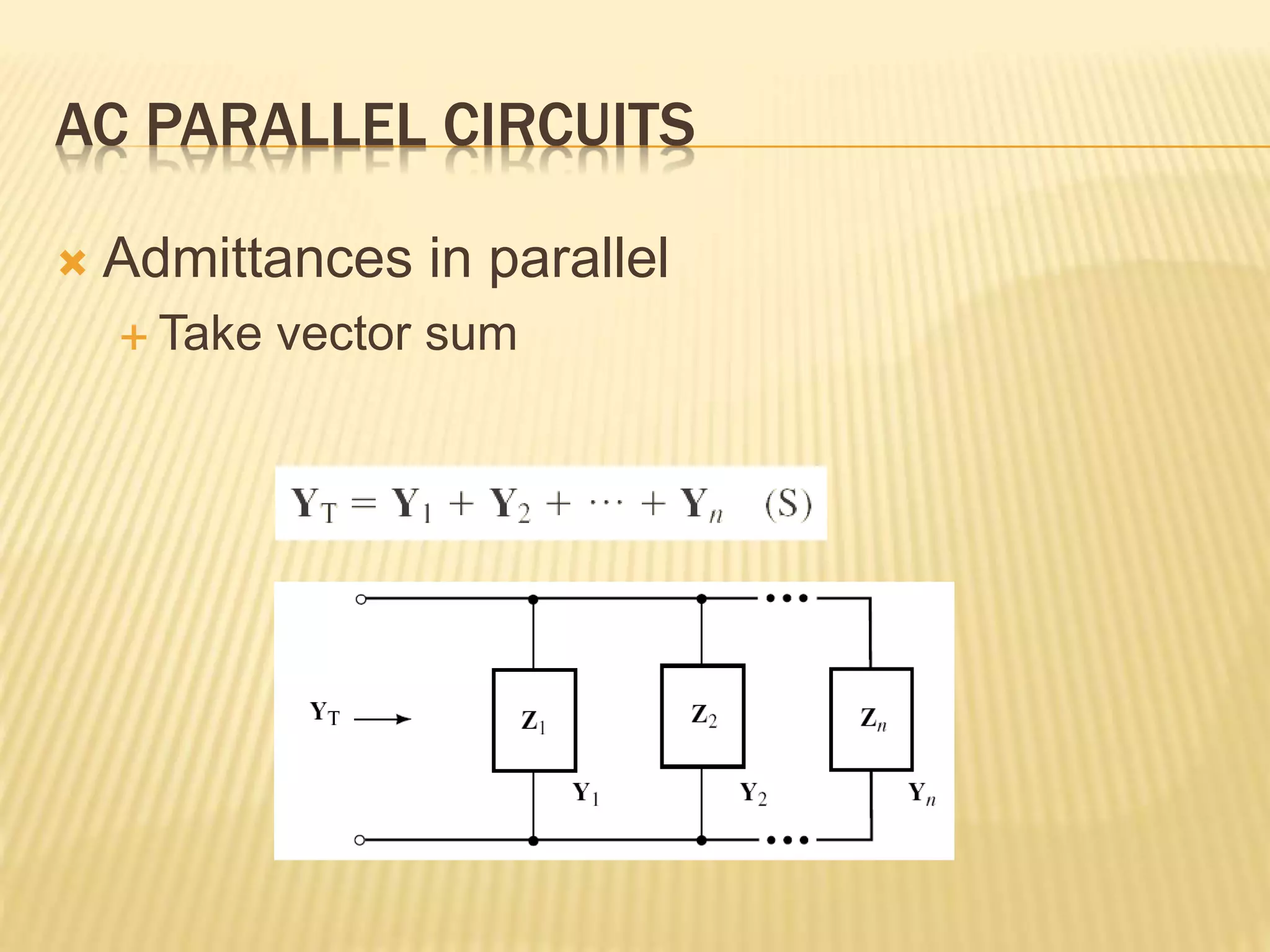
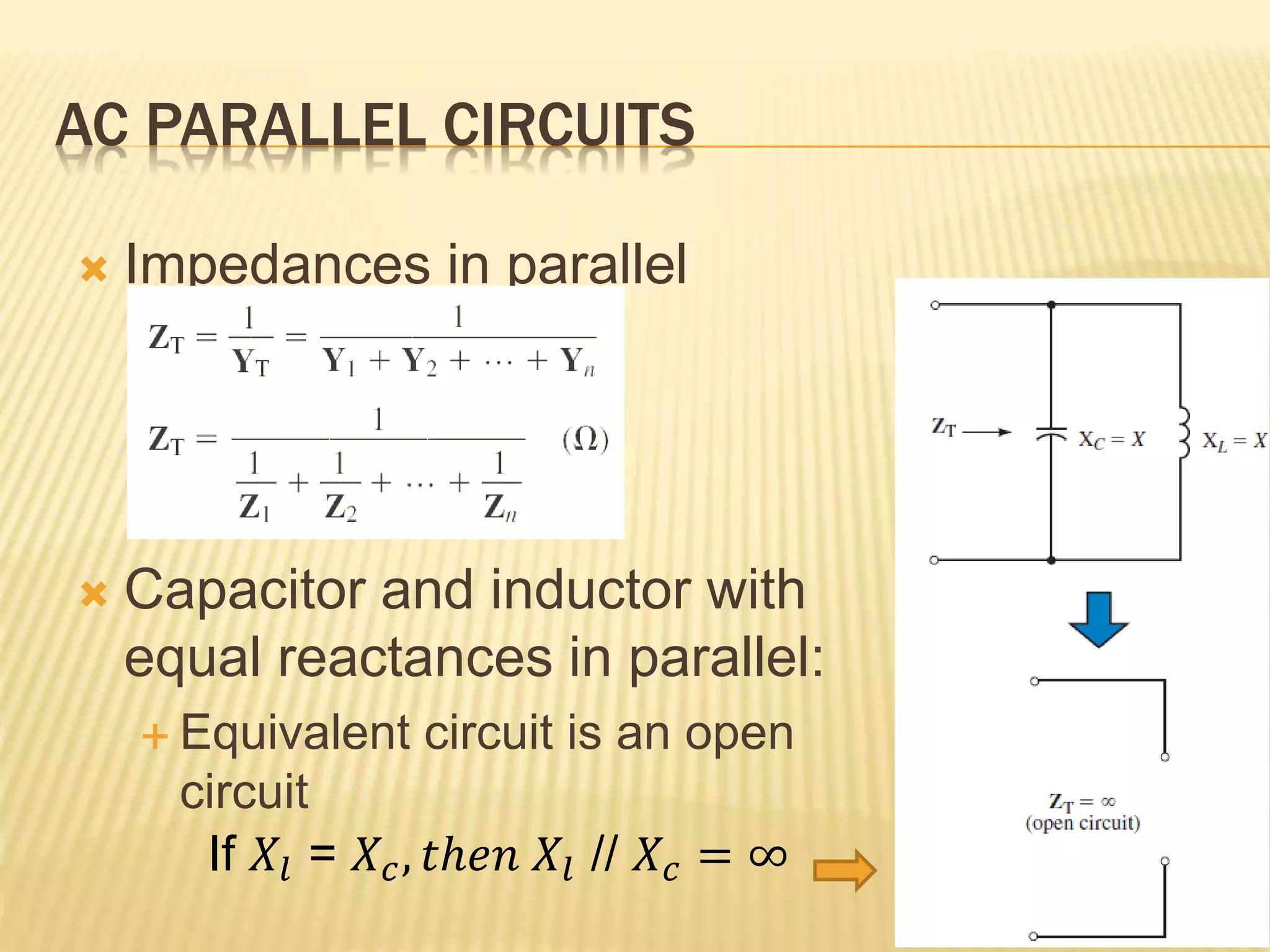
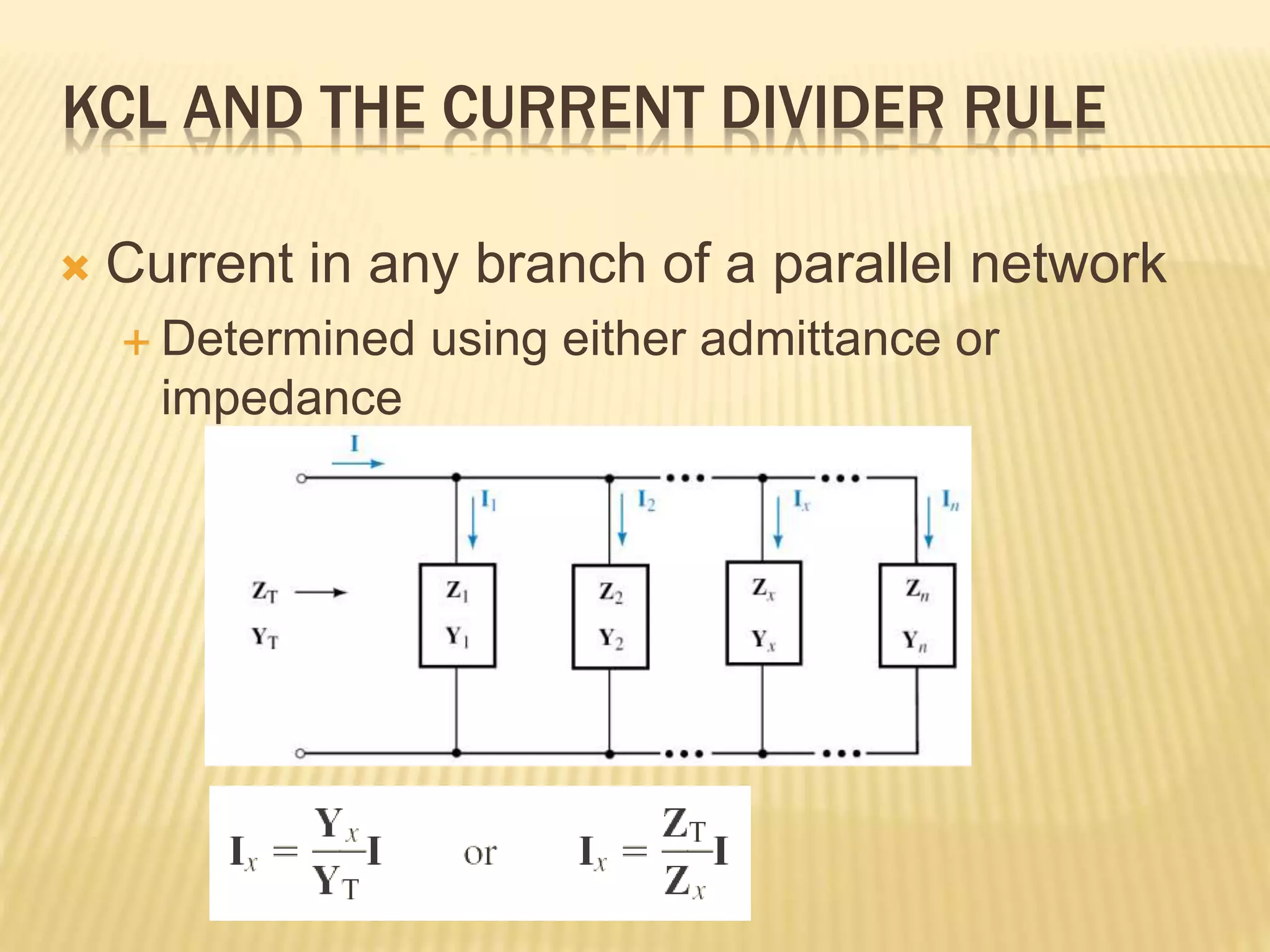
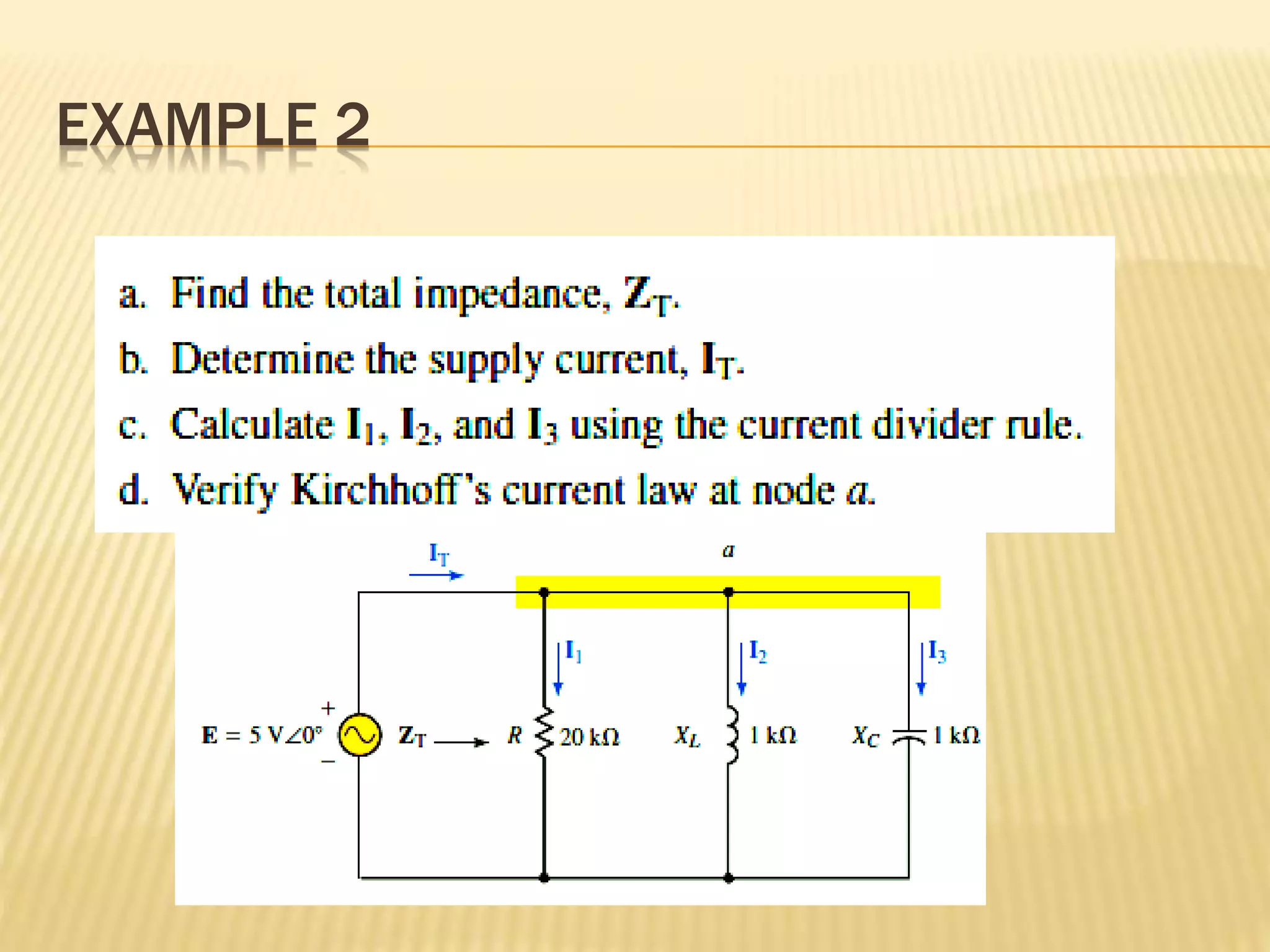
This document discusses AC series-parallel circuits. It defines key concepts like impedance, admittance, susceptance and how they apply to resistors, inductors and capacitors in AC circuits. The document also covers Ohm's law, voltage and current dividers, and Kirchhoff's laws for analyzing AC series, parallel and combined series-parallel circuits through examples and tutorials. Analysis of AC circuits involves determining impedances, admittances, voltages and currents using vector operations in phasor domain.

1. ELECTRICAL CIRCUITS

2. LECTURE 9
AC SERIES-PARALLEL CIRCUITS

3. OHM’S LAW FOR AC CIRCUITS
 Resistors
 Voltage and current through a resistor will
always be in phase

4. OHM’S LAW FOR AC CIRCUITS
 Inductors
 Current in the inductor may be expressed as:
 Where XL = ωL = 2π f L

5. OHM’S LAW FOR AC CIRCUITS
 Capacitors
 Current in the capacitor may be expressed as:
 Where:

6. AC SERIES CIRCUITS
 Current everywhere in a series circuit is the
same
 Impedance
 Term used to collectively determine how
resistance, capacitance, and inductance impede
current in a circuit

7. AC SERIES CIRCUITS
 Impedance diagram
 Total impedance in a
circuit
 Found by adding
individual impedances
vectorially

8. AC SERIES CIRCUITS
 Impedance vectors will appear in either the
first or fourth quadrants:
 Because the resistance vector is always positive
-

9. AC SERIES CIRCUITS
 If impedance vector appears in fourth
quadrant:
 Circuit is capacitive
 If impedance vector appears in first quadrant:
 Impedance is inductive
 Resistive circuit
 Total impedance has only a real component

10. IN SERIES
 Example

11. The polar From

12. EQUAL XL AND XC

13. EXAMPLE

14. KVL AND THE VOLTAGE DIVIDER RULE
 Voltage divider rule for any series
combination of elements
 KVL for ac circuits
 The phasor sum of voltage drops and voltage
rises around a closed loop is equal to zero

15. AC PARALLEL CIRCUITS
 Admittance, Y
 Reciprocal of the impedance
 Units are siemens (S)
 Admittance of a resistor, YR

16. AC PARALLEL CIRCUITS
 Susceptance, B
 Admittance of a purely reactive component X
 Subscripts L and C indicate inductive and
capacitive susceptance

18. AC PARALLEL CIRCUITS
 Admittances in parallel
 Take vector sum

19. AC PARALLEL CIRCUITS
 Impedances in parallel
 Capacitor and inductor with
equal reactances in parallel:
 Equivalent circuit is an open
circuit
If 𝑋𝑙 = 𝑋𝑐, 𝑡ℎ𝑒𝑛 𝑋𝑙 // 𝑋𝑐 = ∞

20. AC PARALLEL CIRCUITS
 For two impedances:
 Three impedances in parallel

21. KCL AND THE CURRENT DIVIDER RULE
 Current in any branch of a parallel network
 Determined using either admittance or
impedance

22.  For two branches in parallel:
 KCL for ac circuits
 Summation of current phasors entering and
leaving a node equals zero
KCL AND THE CURRENT DIVIDER RULE

23. SERIES-PARALLEL CIRCUITS
 Simplify analysis
 Start with easily recognized combinations
 Redraw circuit if necessary
 Fundamental laws of circuit analysis apply in
all cases

24. TUTORIAL
AC SERIES-PARALLEL CIRCUITS

25. Example 1
a) Find ZT
b) Sketch the impedance diagram (phasor) for the network and
indicate whether the total impedance of the circuit is
inductive, capacitive, or resistive.
c) Use Ohm’s law to determine I, VR, and VC. (Phasor domain)

28. EXAMPLE 2

30. Example 3

32. -

33. EXAMPLE 4
A circuit has a total impedance ZT
=10Ω+j50Ω sketch the equivalent series
circuit

35. EXAMPLE 5
 A circuit has a total impedance YT
=0.559mS∟63.43o sketch the equivalent parallel
circuit