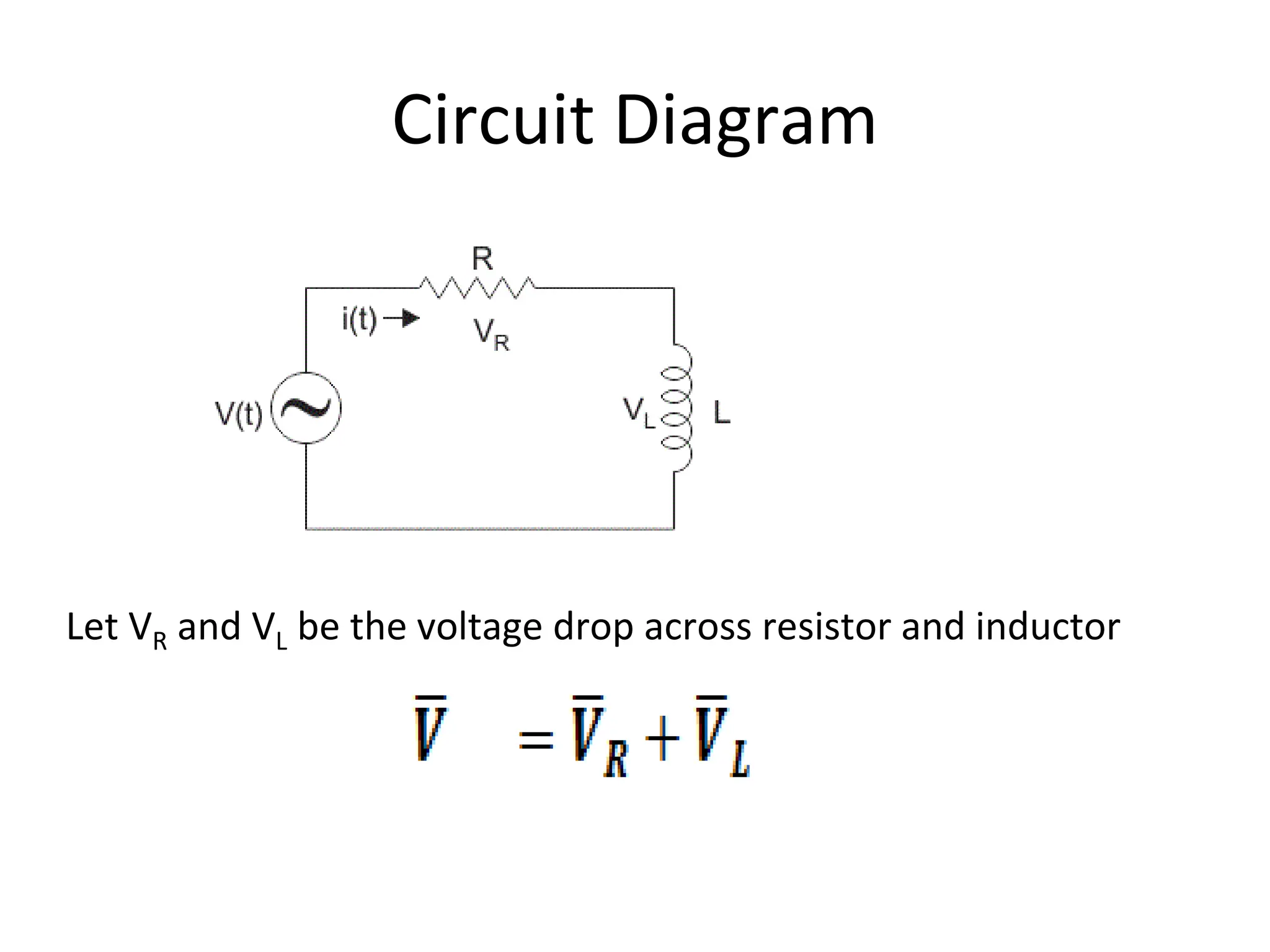
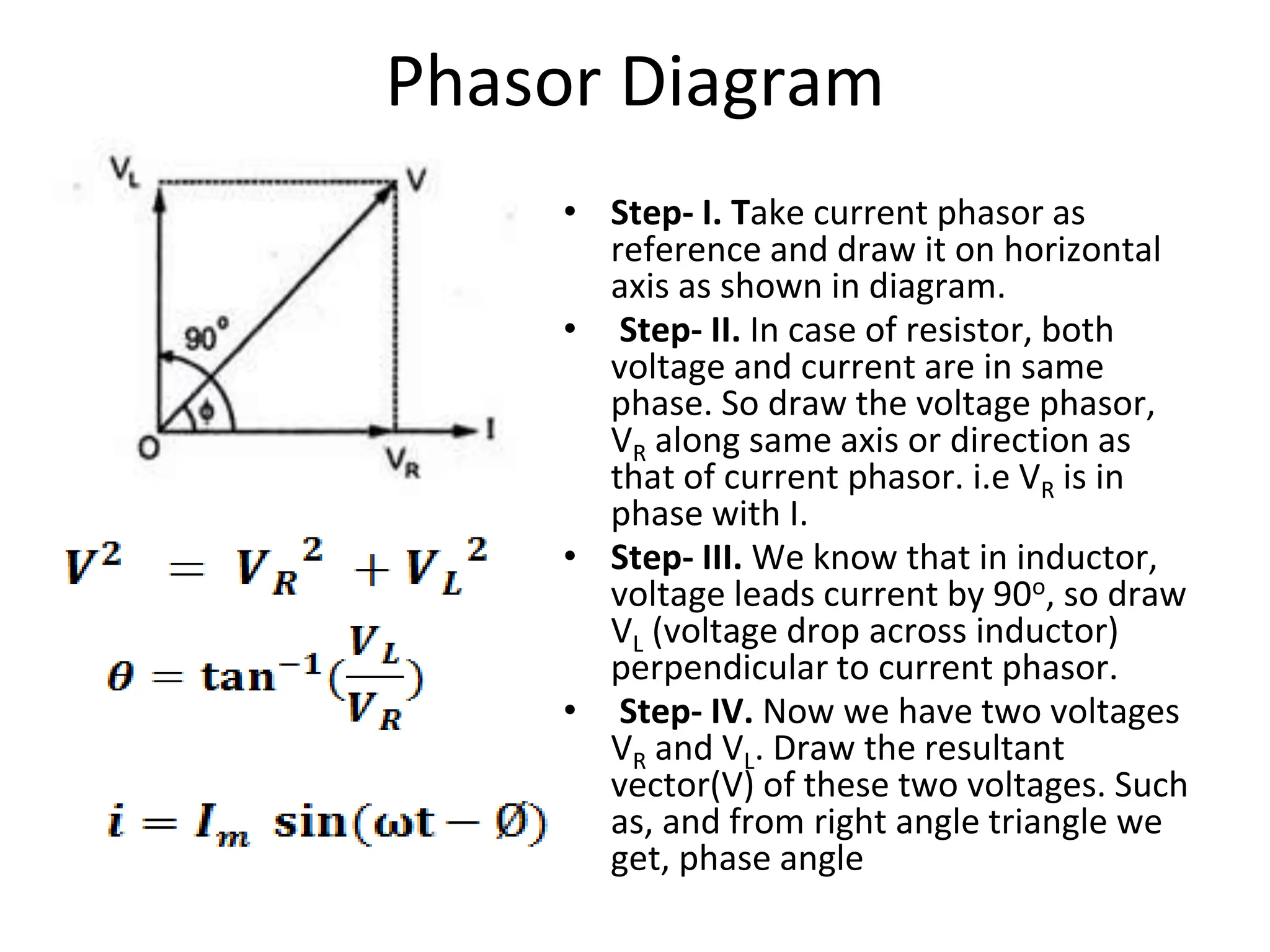
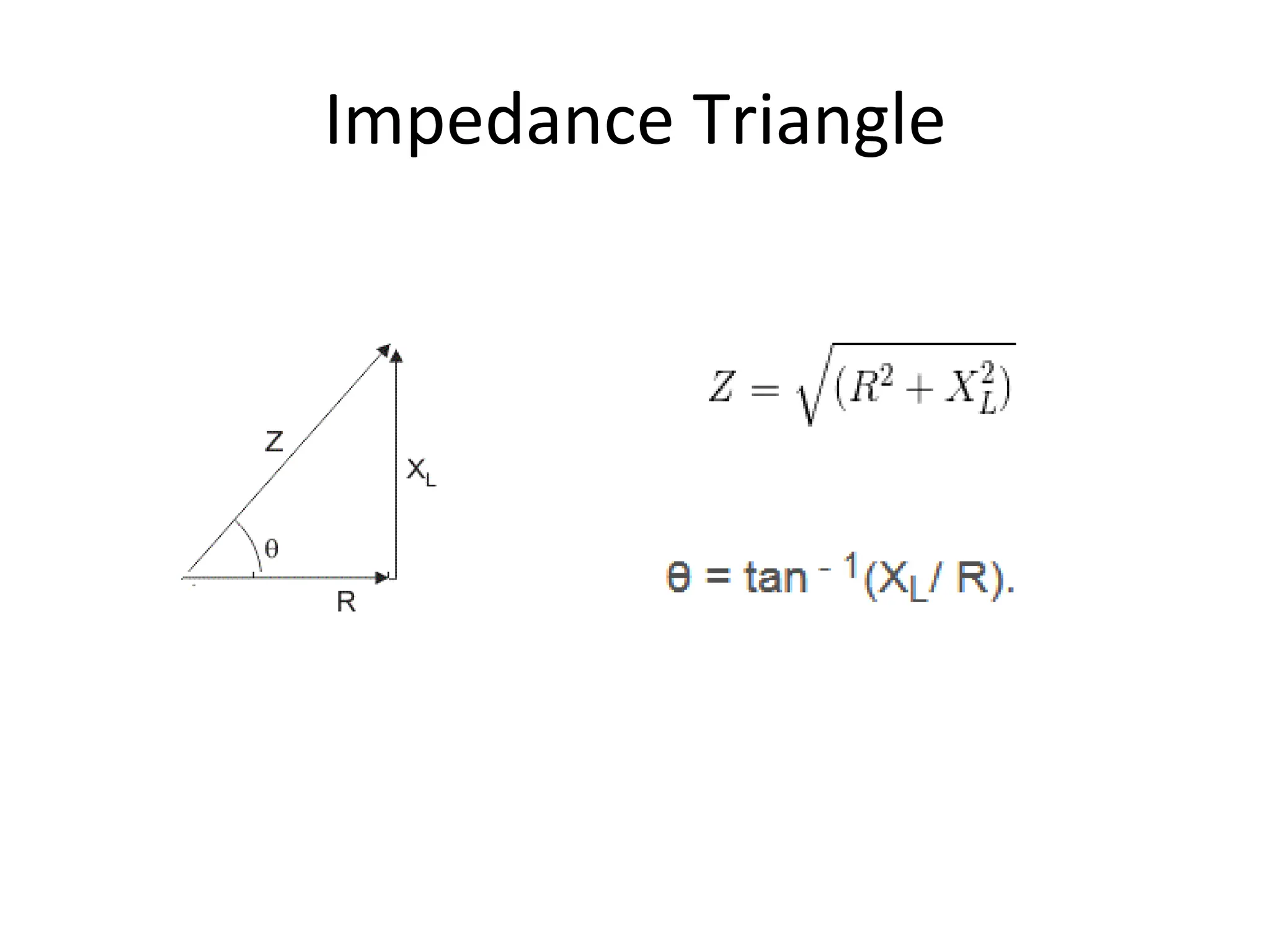
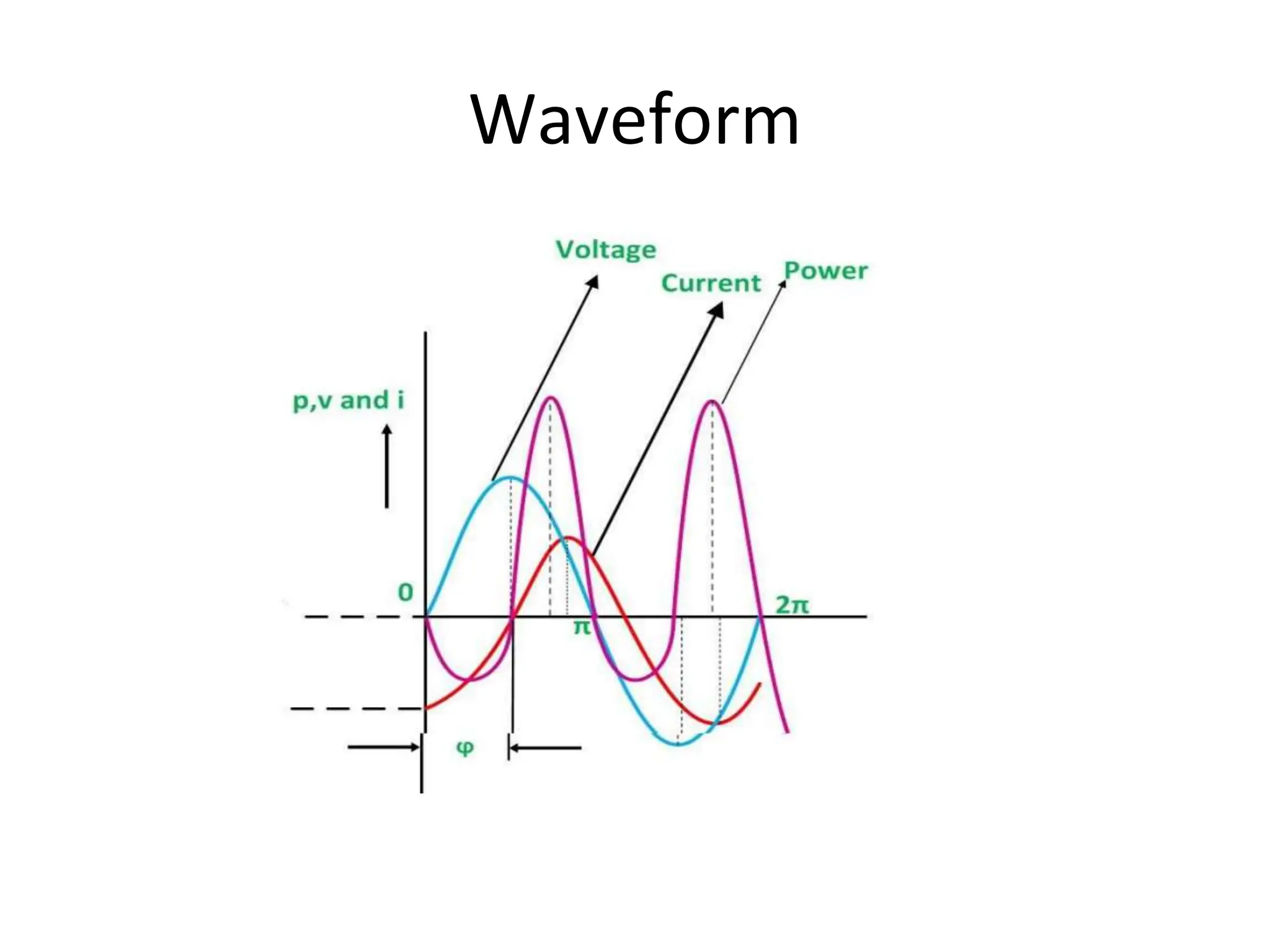
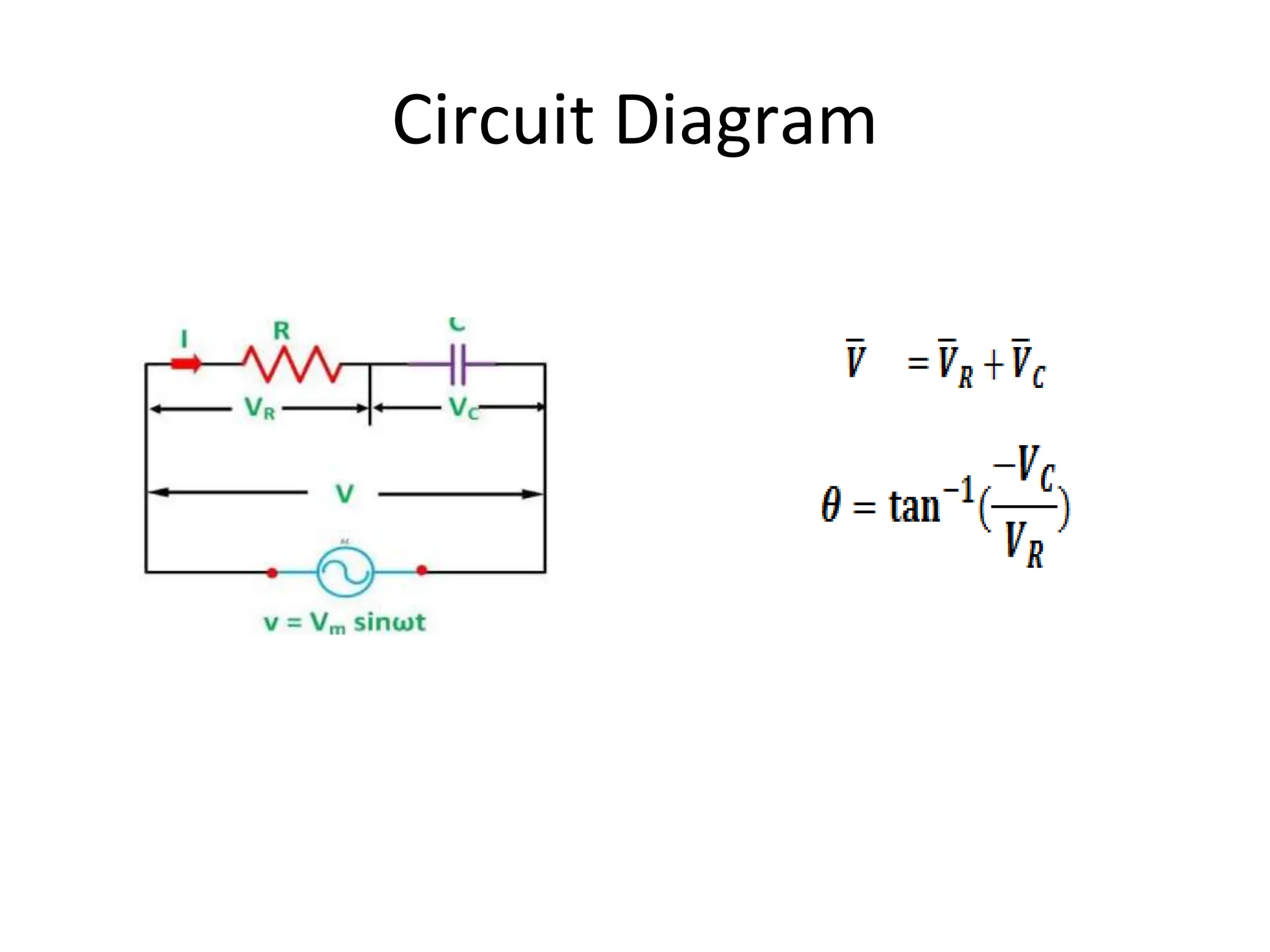
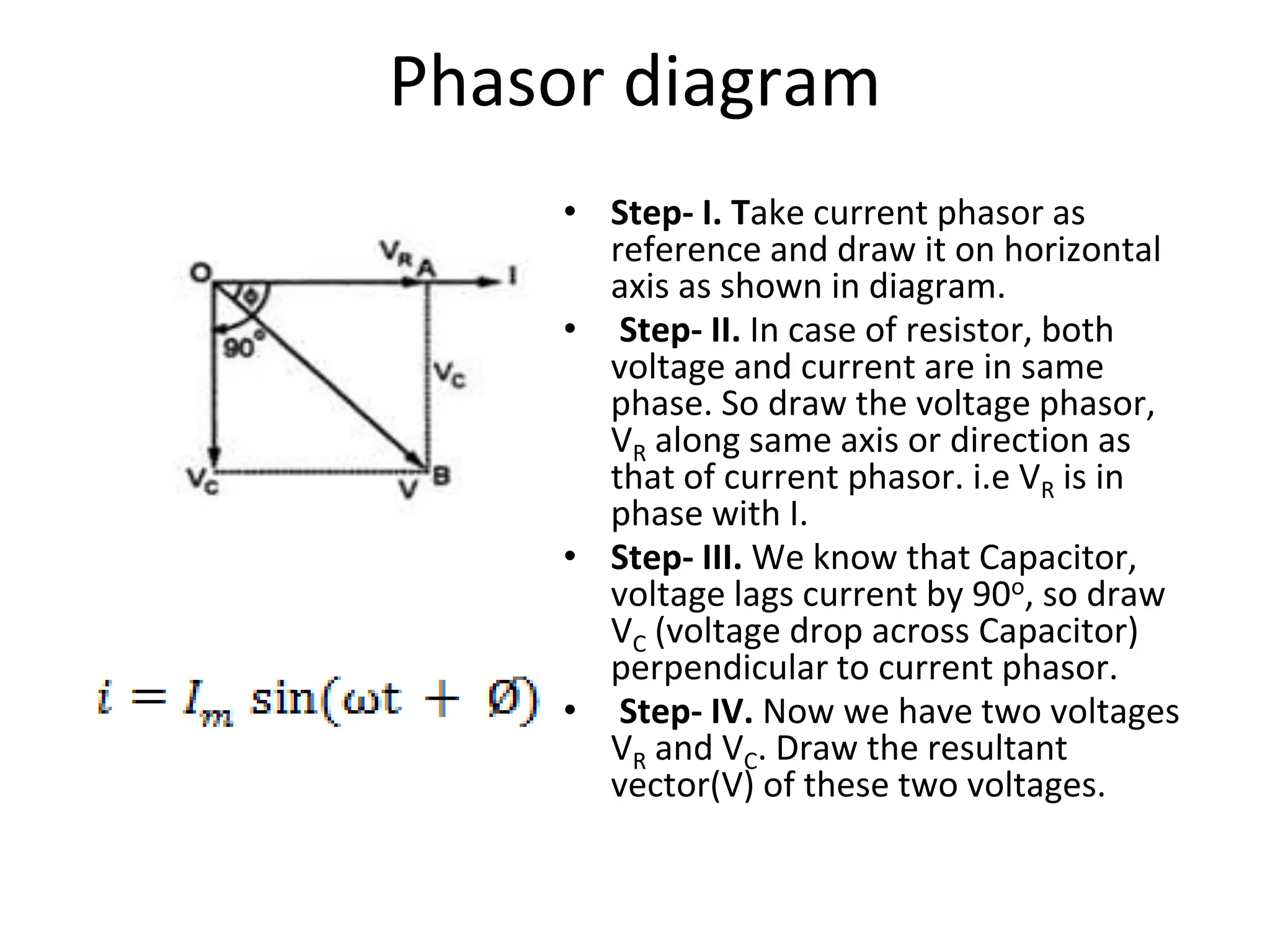
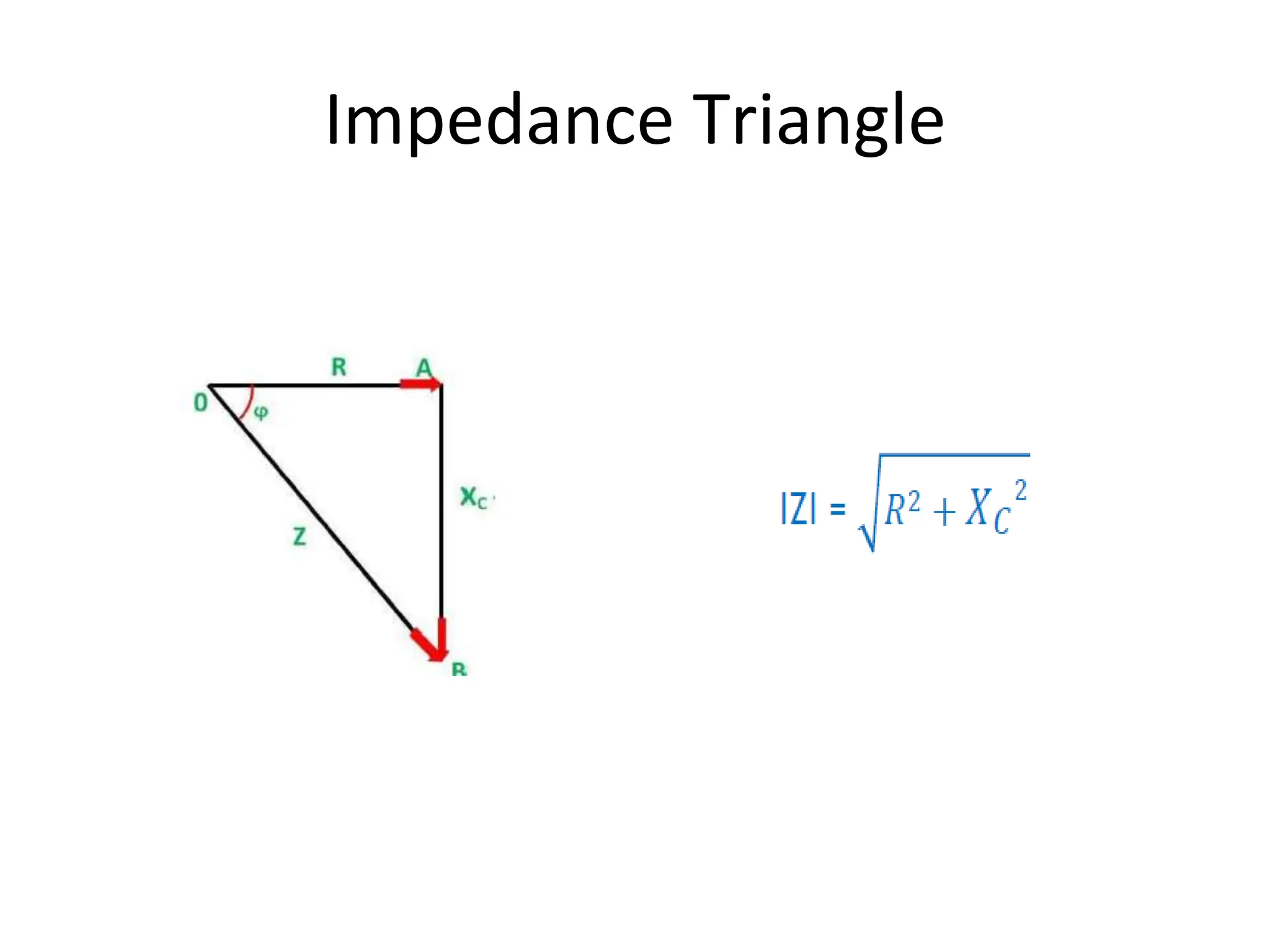
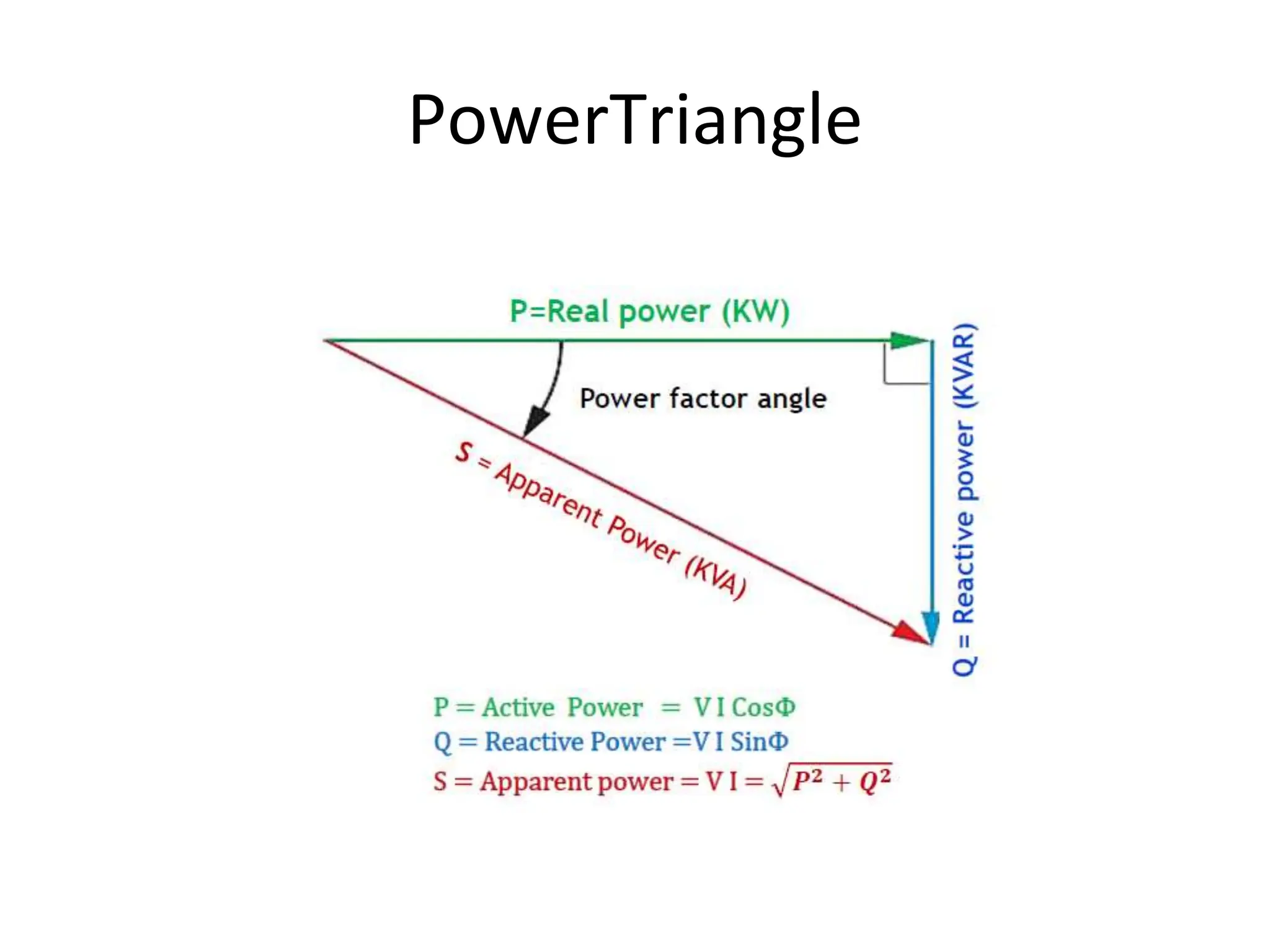
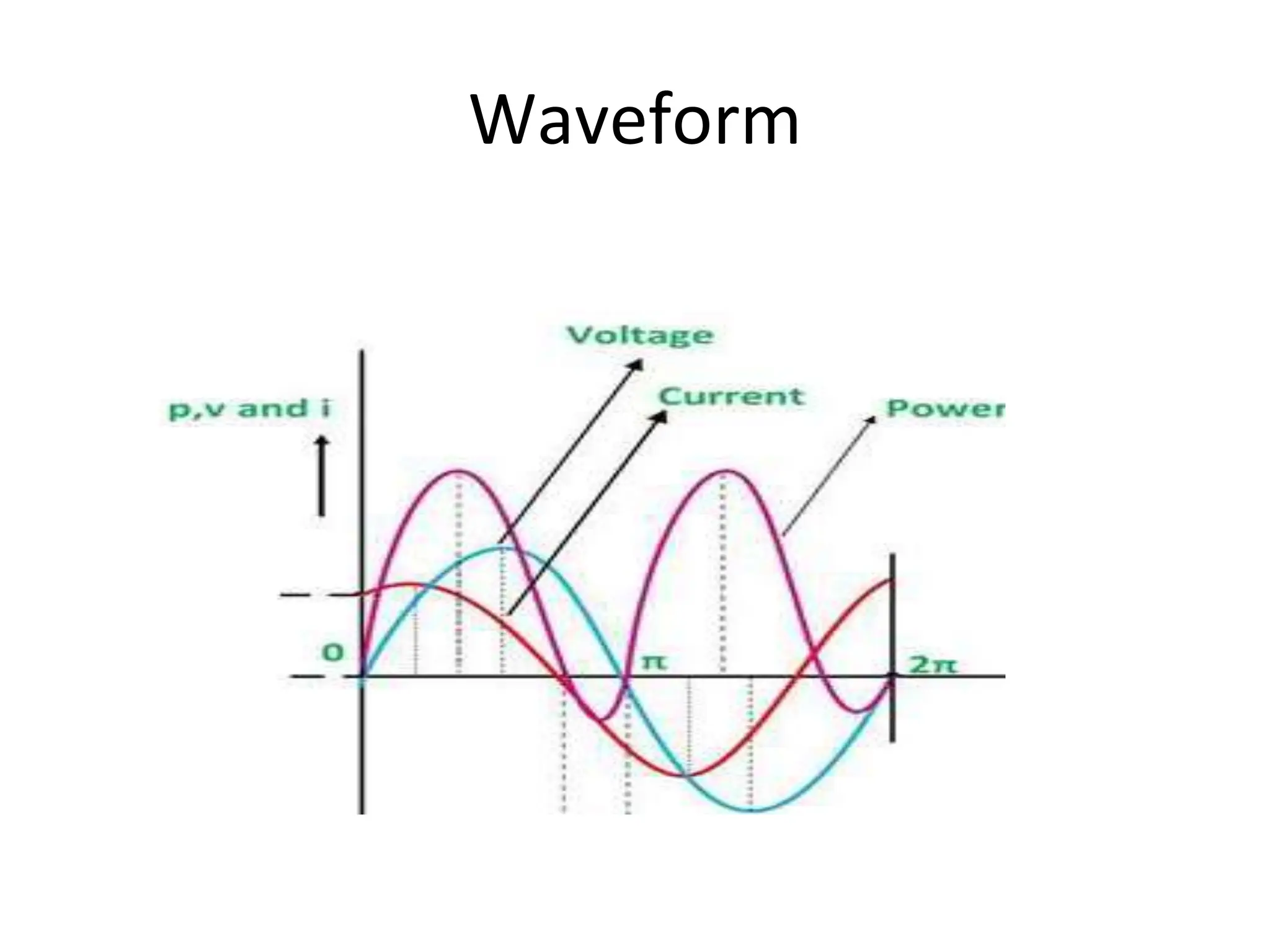
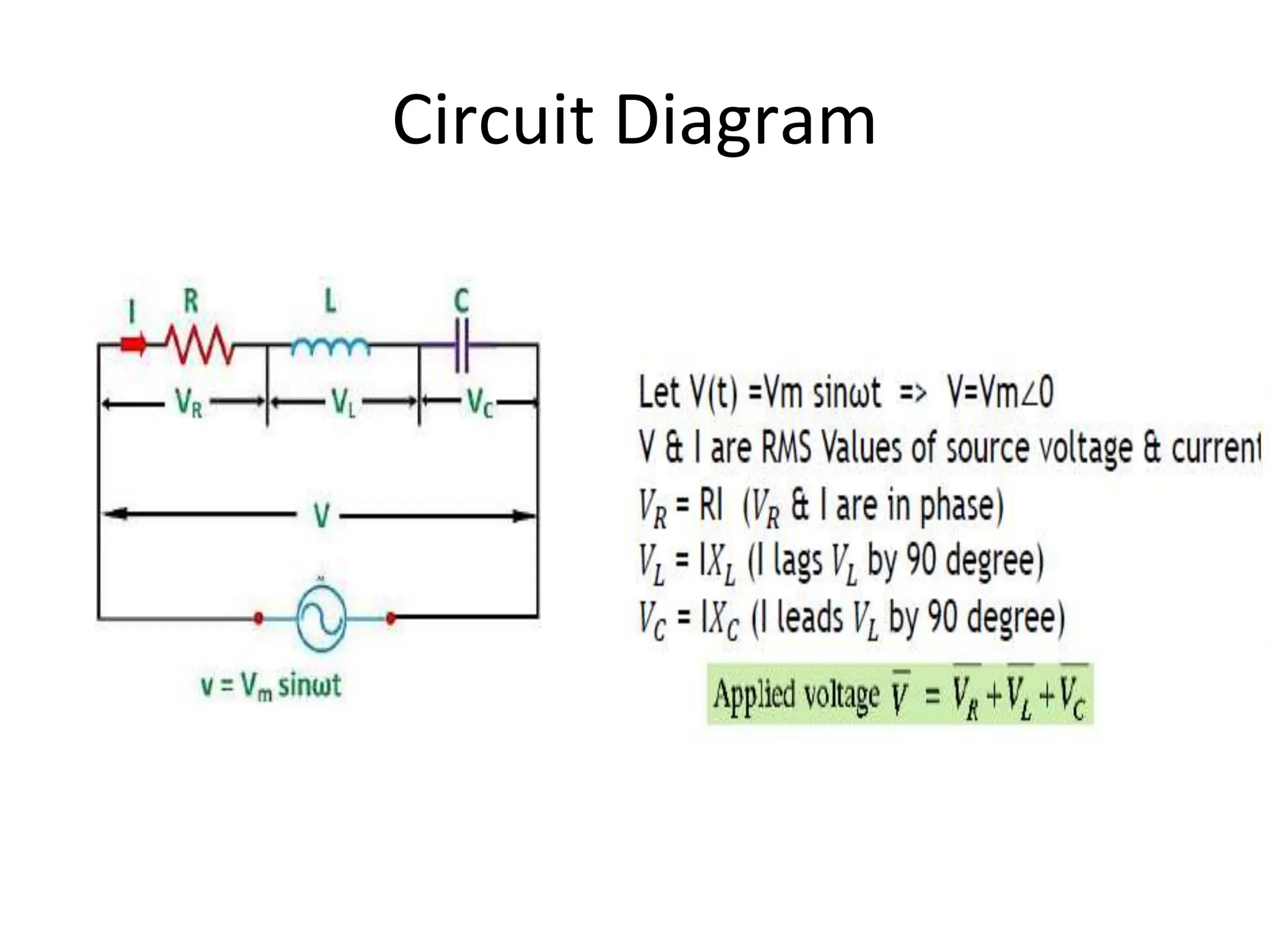
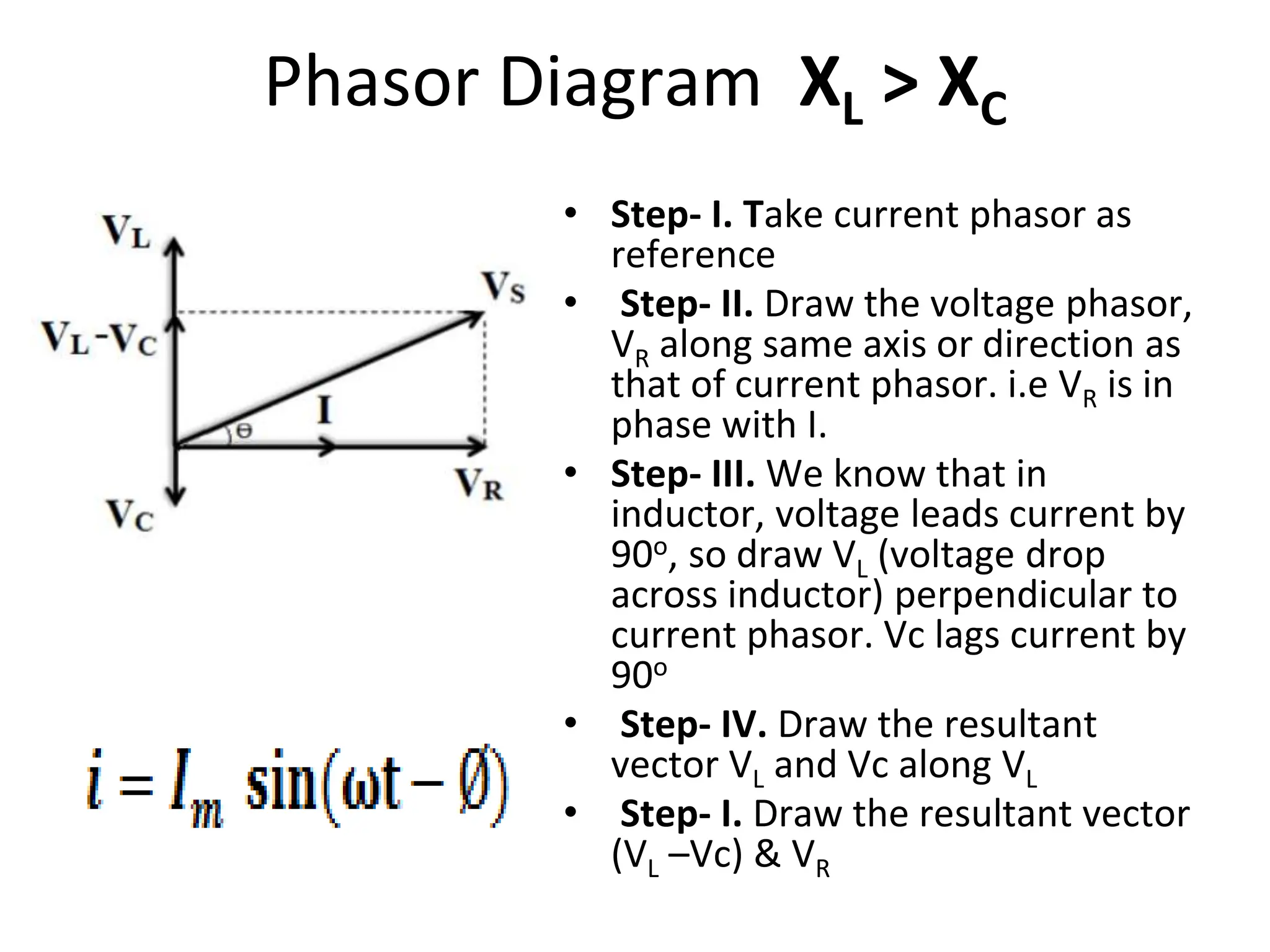
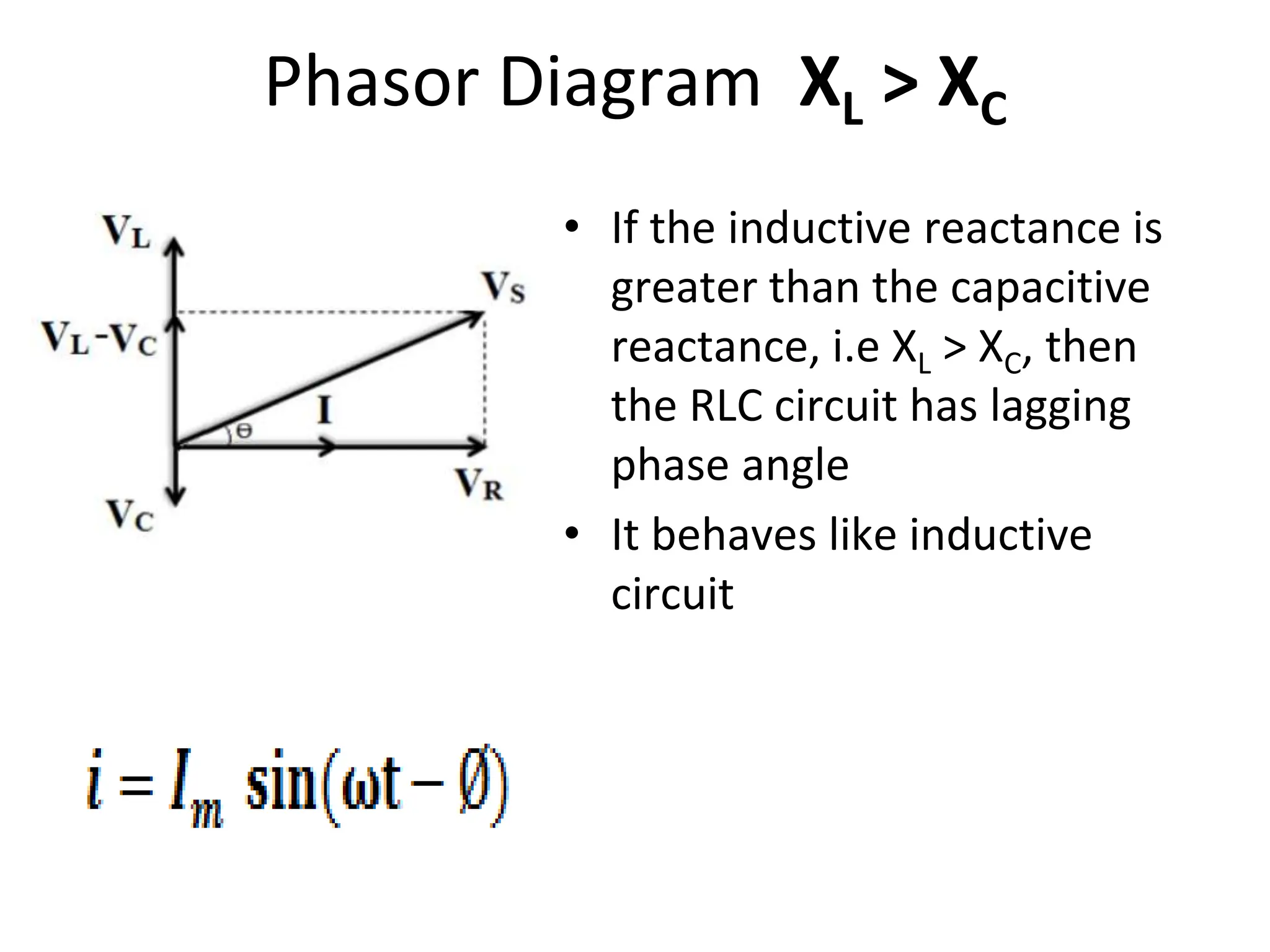
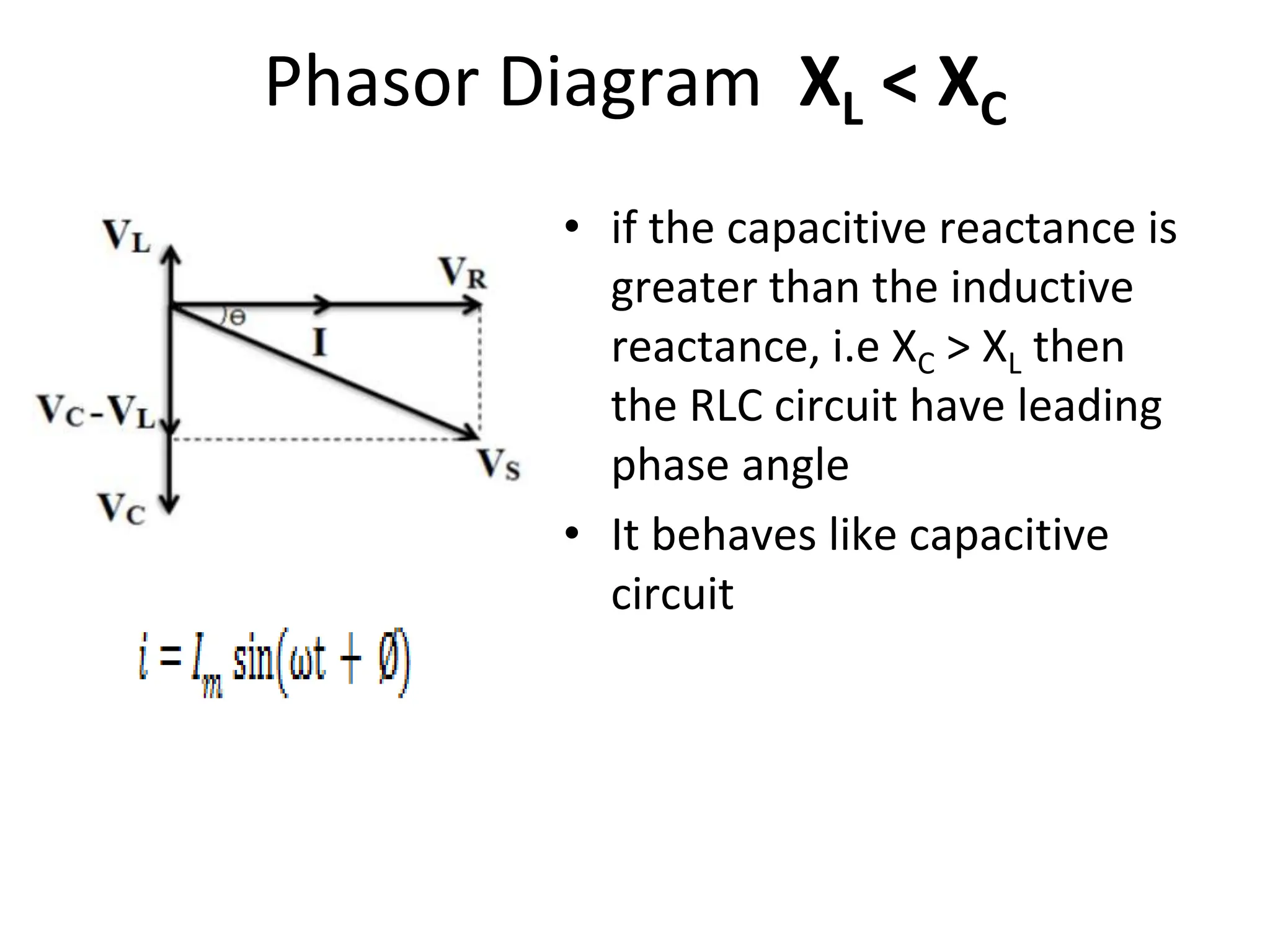
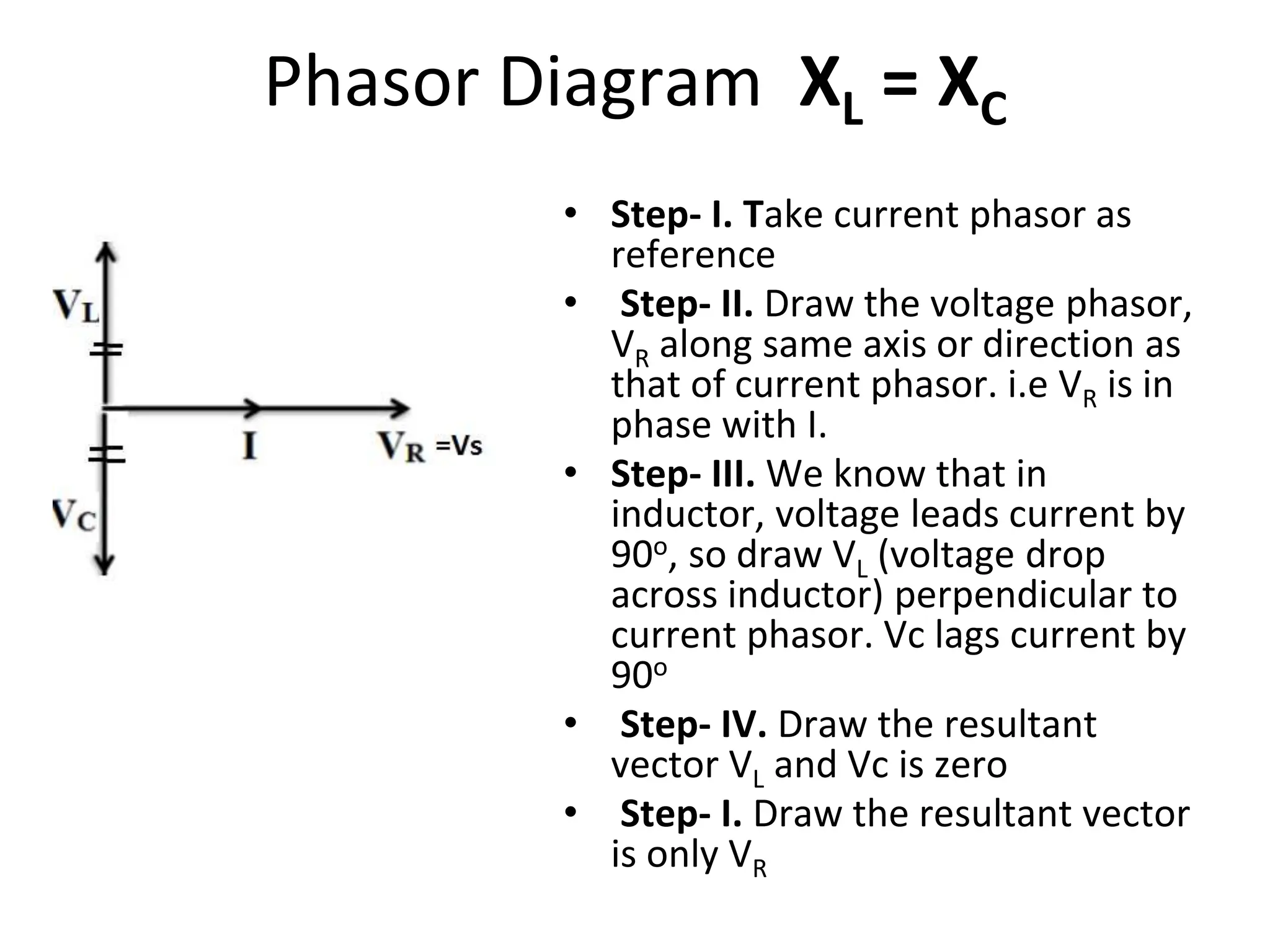
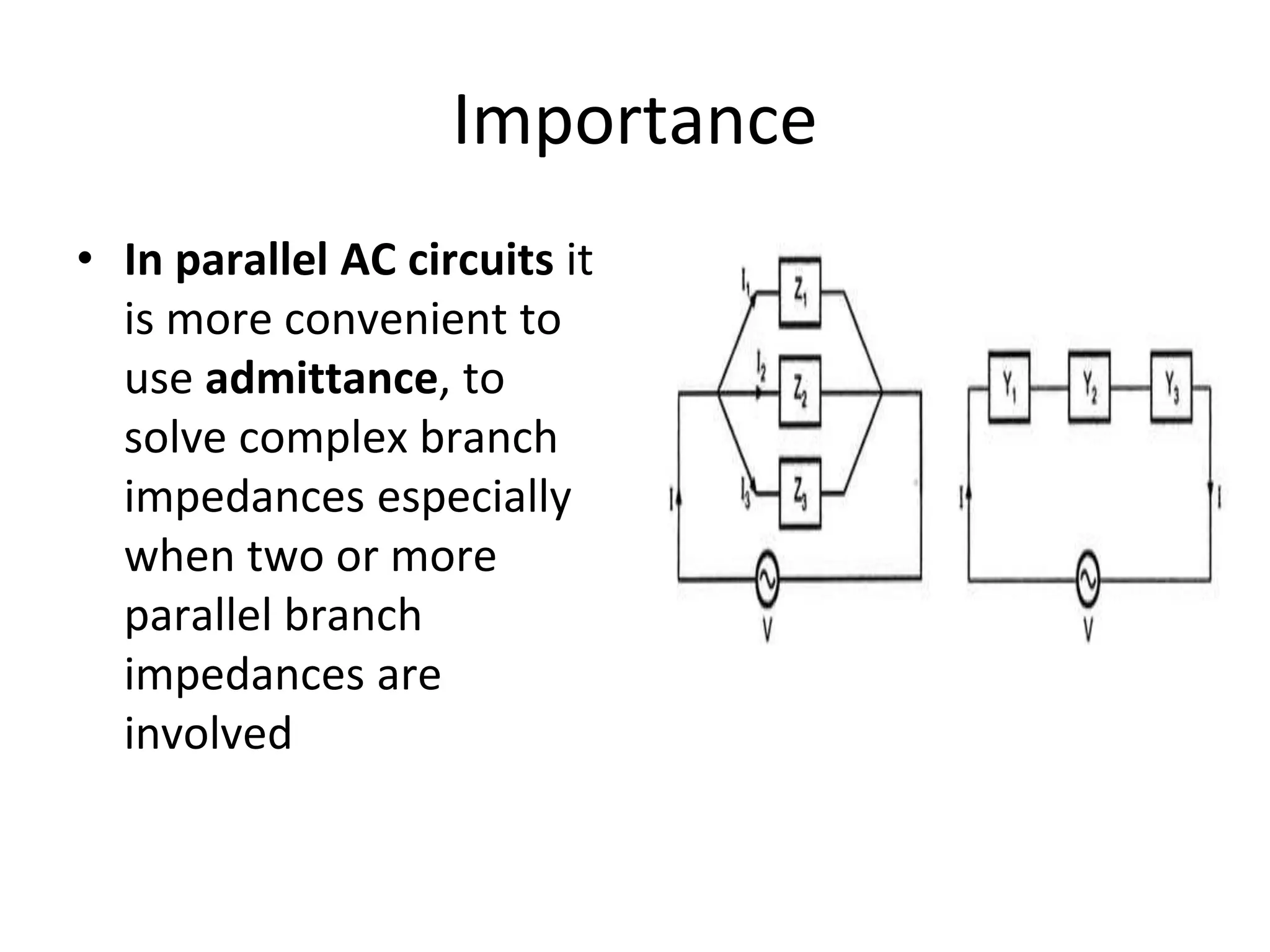
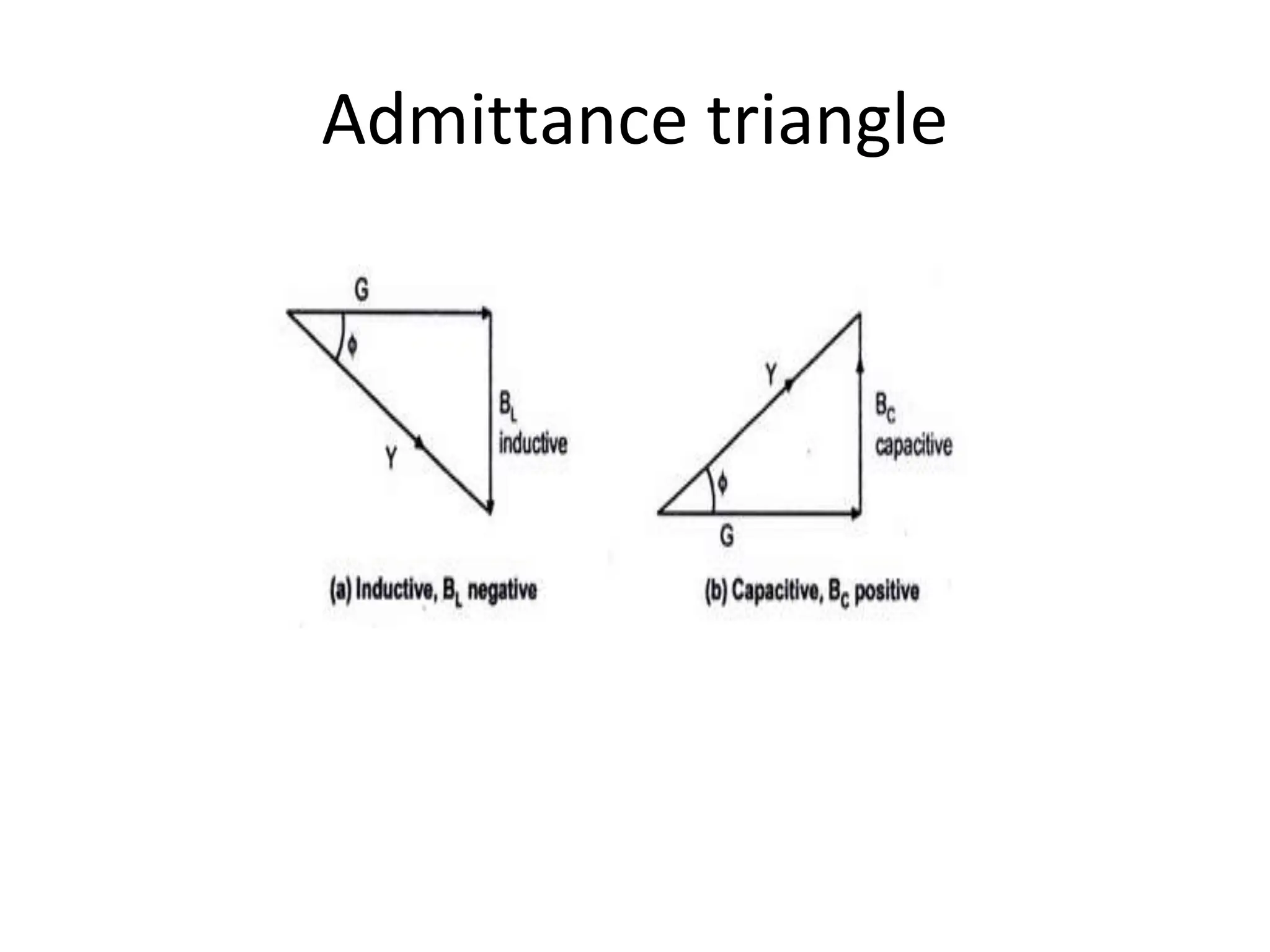
The document outlines the objectives and analysis of series RL, RC, and RLC circuits, focusing on their voltage-current relationships, impedance, phase angles, and power calculations. It includes phasor diagrams and waveform summaries demonstrating the behavior of current and voltage in these circuits, highlighting how impedance varies with frequency and the conditions for resonance. Additionally, it introduces the concept of admittance as the reciprocal of impedance, emphasizing its utility in solving parallel AC circuits.