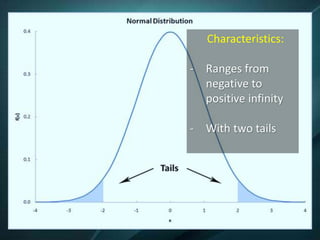
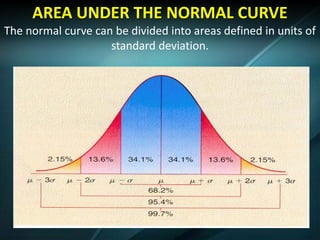
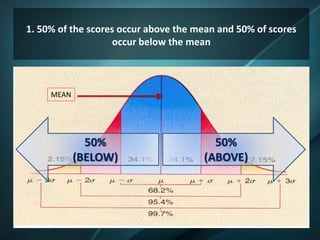
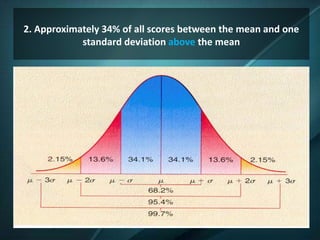
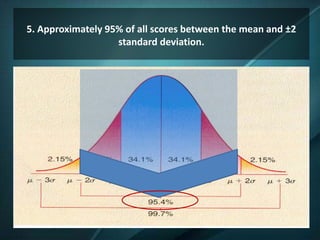
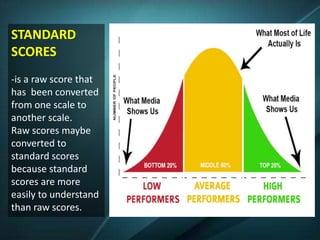
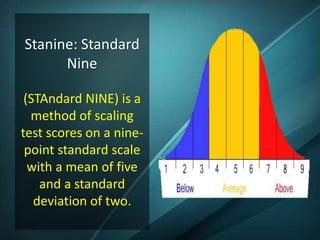
The document discusses the normal curve and standard scores. It defines the normal curve as a continuous probability distribution that is bell-shaped and symmetric. It was developed by Gauss and Pearson. The normal curve can be divided into areas defined by standard deviations from the mean. Standard scores are raw scores converted to other scales, including z-scores, t-scores, and stanines. Z-scores indicate the distance from the mean in standard deviations. T-scores are on a scale of 50 plus or minus 10. Stanines use a nine-point scale with a mean of 5 and standard deviation of 2.

1. TOPIC OUTLINE:
1. The Normal Curve
a. Definition/Description
b. Area Under Normal Curve
2. Standard Scores
a. Z-Scores
b. T-Scores
c. Other Standard Scores

2. NORMAL CURVE
- Karl Friedrich
Gauss:
one of the scientist
that developed the
concept of normal
curve.
Common term:
Laplace-Gaussian
Curve or Gaussian

3. * Normal Curve
is a continuous
probability distribution
in statistics
Karl Pearson:
first to refer to the
curve as “Normal
Curve”
NORMAL CURVE
- Karl Friedrich
Gauss:
one of the scientist
that developed the
concept of normal
curve.
Common term:
Laplace-Gaussian
Curve or Gaussian

4. Characteristics:
- Smooth bell shaped curved
- Asymptotic: approaching
the x-axis but never
touches it
- Symmetric: made up of
exactly similar parts facing
each other

5. Characteristics:
- Ranges from
negative to
positive infinity
- With two tails

6. A normal curve has two tails.
• The area on the normal curve between 2 and 3
standard deviations above the mean is referred to as a
tail.
• The area between -2 and -3 standard deviations below
the mean is also referred to as a tail.

7. AREA UNDER THE NORMAL CURVE
The normal curve can be divided into areas defined in units of
standard deviation.

8. 1. 50% of the scores occur above the mean and 50% of scores
occur below the mean
50%
(ABOVE)
50%
(BELOW)
MEAN

9. 2. Approximately 34% of all scores between the mean and one
standard deviation above the mean

10. 3. Approximately 34% of all scores between the mean and one
standard deviation bellow the mean

11. 4. Approximately 68% of all scores between the mean and ±1
standard deviation.

12. 5. Approximately 95% of all scores between the mean and ±2
standard deviation.

13. STANDARD
SCORES
-is a raw score that
has been converted
from one scale to
another scale.
Raw scores maybe
converted to
standard scores
because standard
scores are more
easily to understand
than raw scores.

14. Different systems:

15. Z-scores
- called a zero plus or minus one
scale
- results from the conversion of a
raw score into a number
indicating how many standard
deviation units the raw score is
below or above he mean of the
distribution.
- Scores can be positive and
negative

16. Z-scores
- X - raw score
- U - mean
- Q - standard deviation
x
z





17. T-Scores
- The scale used in the computation of t-
scores can be called a 50 plus or minus ten
scale. ( 50 mean set and 10 SD set )
- Composed of scale ranges from 5 SD below
the mean to5 SD above the mean.
- One advantage in using T-Scores is that none
of the scores is negative.

18. Page 99
- SD = 15
- Mean = 50
Process:
Value = (mean + (number of deviation x 1 standard deviation) )
65 = ( 50 + ( 1 X 15 )
Value = (mean – (number of deviation x 1 standard deviation) )
35 = ( 50 – ( 1 X 15 )
X bar + 1s = 50 + 15 =
X bar - 1s = 50 - 15 =

19. Stanine: Standard
Nine
(STAndard NINE) is a
method of scaling
test scores on a nine-
point standard scale
with a mean of five
and a standard
deviation of two.

20. SUMMARY:
Karl Friedrich Gauss:
one of the scientist that developed the
concept of normal curve.
Normal Curve
is a continuous probability distribution in
statistics
Karl Pearson:
first to refer to the curve as “Normal
Curve”
Asymptotic:
approaching the x-axis but never touches it
Symmetric:
made up of exactly similar parts facing
each other
STANDARD SCORES
-is a raw score that has been converted
from one scale to another scale.
Z-scores
called a zero plus or minus one scale
Scores can be positive and negative
T-Scores
a none of the scores is negative. It can be
called a 50 plus or minus ten scale. ( 50
mean set and 10 SD set )
Stanine: Standard Nine
(STAndard NINE) is a method of scaling
test scores on a nine-point standard scale
with a mean of five and a standard
deviation of two.

21. Reanne Mariquit
AB PSYCHOLOGY
Rhea Moring
AB PSYCHOLOGY
Ace Matilac
AB PSYCHOLOGY
UNIVERSITY OF IMMACULATE CONCEPTION
Davao City, Philippines
© 2015
Reference: Cohen, Swerdilik, & Sturman (2013). Psychological Testing and
Assessment: An Introduction to Test and Measurement, Eight h Edition.
Philippines: McGrawHill Education.

22. Reanne Mariquit
AB PSYCHOLOGY
Rhea Moring
AB PSYCHOLOGY
Ace Matilac
AB PSYCHOLOGY
UNIVERSITY OF IMMACULATE CONCEPTION
Davao City, Philippines
© 2015
Reference: Cohen, Swerdilik, & Sturman (2013). Psychological Testing and
Assessment: An Introduction to Test and Measurement, Eight h Edition.
Philippines: McGrawHill Education.