Here are the steps I would take to separate the components of this mixture:
1. Filter the mixture to separate the solid components (acetanilide, aluminum oxide, aspirin) from the liquid components (water, methanol).
2. Distill the liquid portion to separate the water from the methanol based on their different boiling points. Collect the methanol distillate and water distillate separately.
3. Use solvent extraction to separate the solid components. Add water to dissolve the aspirin, leaving the acetanilide and aluminum oxide undissolved. Filter to separate the dissolved aspirin from the undissolved solids.
4. The original mixture has now been separated into its pure components which can





















































































































































































































































































































































































































































![AP Only
Example: Find E for the reaction if 1.30 mol of Na react with excess
water at 298 K, given that:
2Na (s) + 2H2O (l) 2NaOH (aq) + H2 (g) ∆H = -367.5 kJ/mol
i. E = ∆H - nRT -- we must find n and H:
1 mol H2
ii. 1.30 mol Na x = 0.650 mol H2 produced
2 mol Na
iii. n = mol product gas – mol reactant gas = (0.650 – 0) = 0.650 mol
-367.5 kJ
iv. H = x 0.650 mol H2 = - 238.9 kJ
1 mol H2
= 1610 J ~ 1.61 kJ
v. E = (-238.9 kJ) - [ (0.650)(8.314 kPa-L/mol K) x 298 K ]
vi. E = - 238.9 kJ – 1.61 kJ = - 240.5 kJ
note that H ≈ E](https://image.slidesharecdn.com/all-chem-notes-130329135633-phpapp01/75/All-chem-notes-483-2048.jpg)
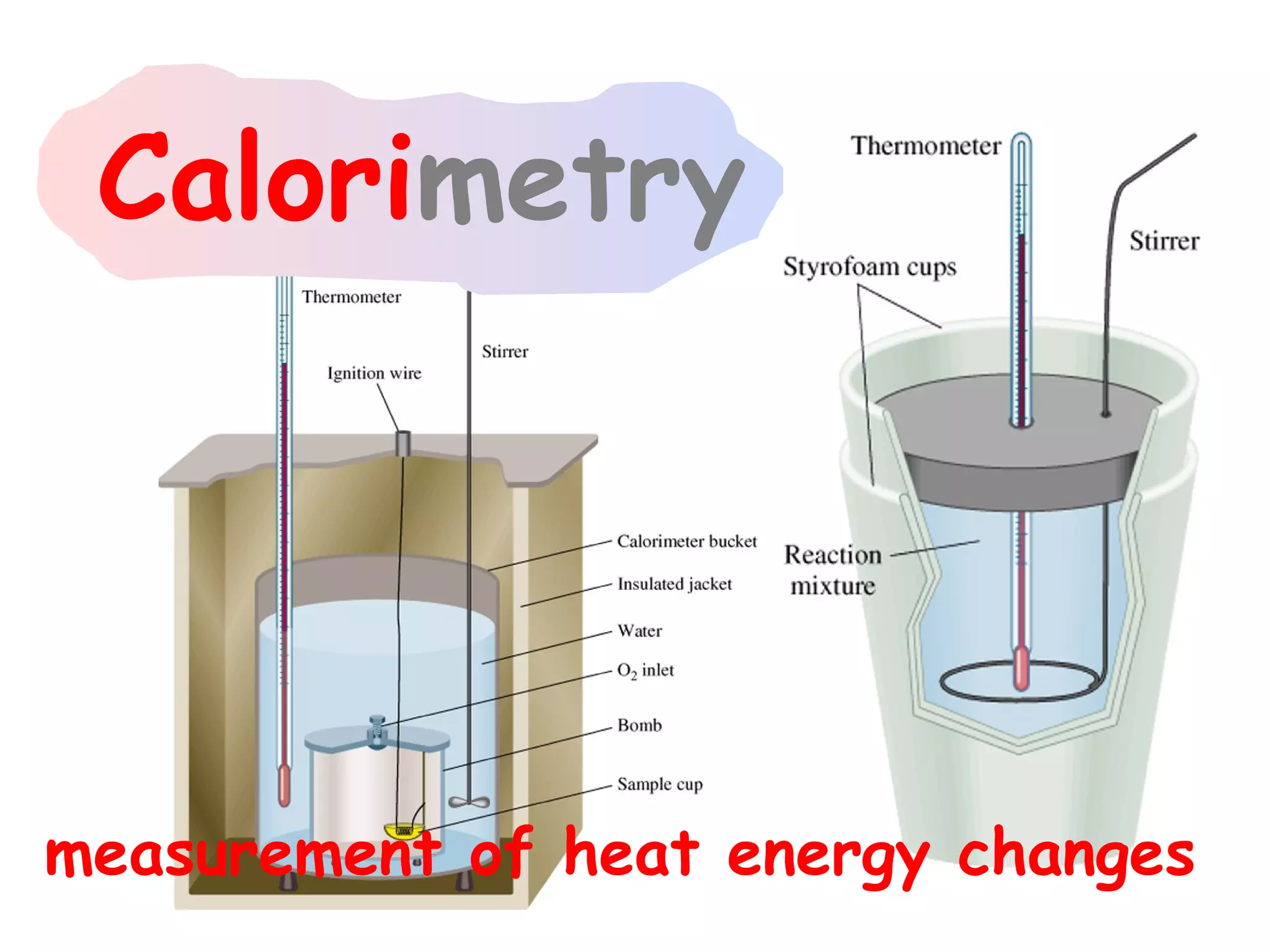









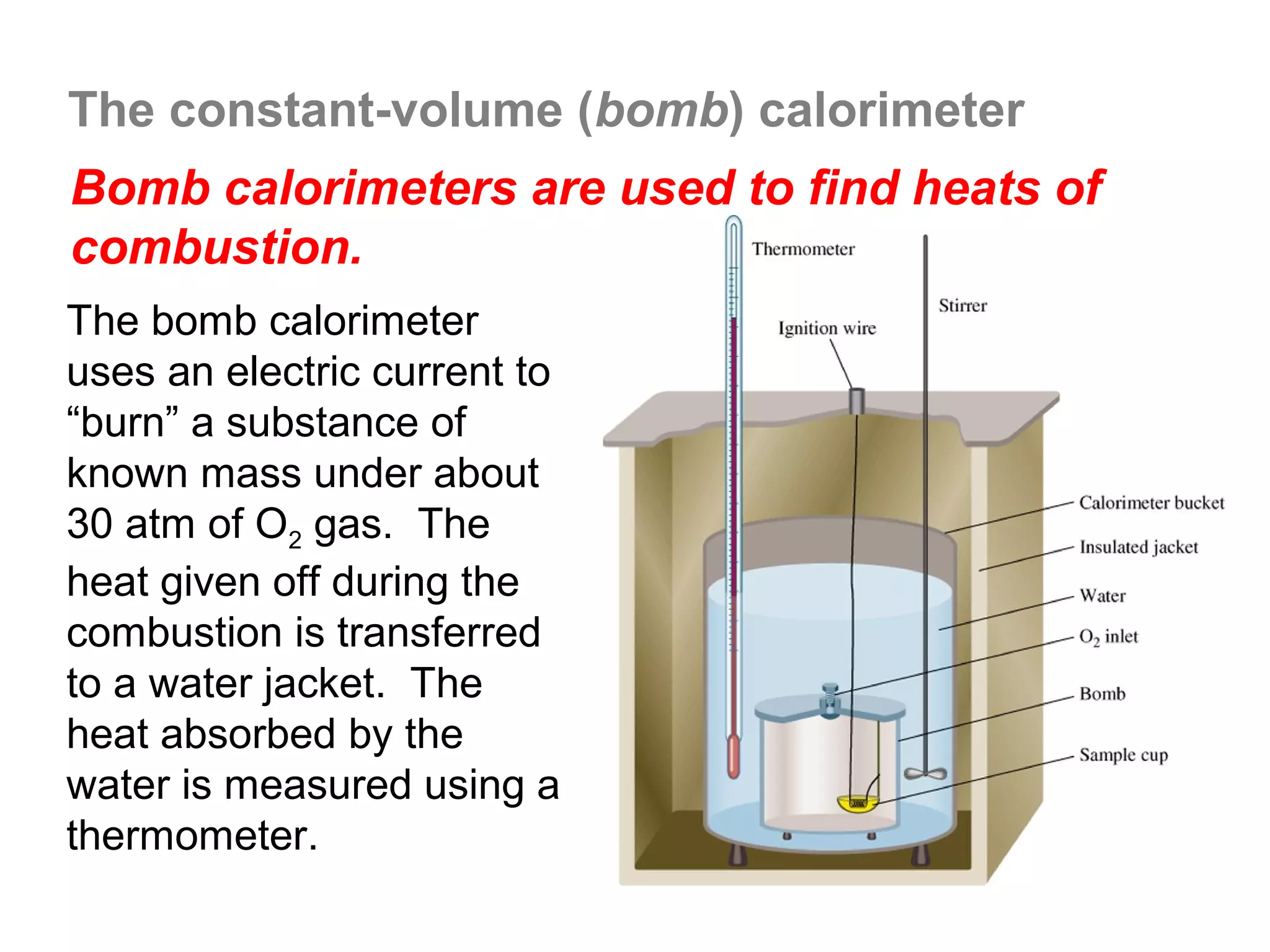

![The Constant-Volume Bomb Calorimeter
qsys = qcal + qrxn
assuming no heat enters or leaves the bomb calorimeter,
we can say that qsys = 0 !
heat given off in the reaction =
- qrxn = + qcal
heat absorbed by the calorimeter
- qrxn = +(qwater + qbomb) qcal = heat absorbed by the
bomb + heat absorbed by the
qwater = cm∆t water jacket…
▪ dimensionally, HC = J/oC so qbomb = HCbomb x t
▪ finally, note that Δt of the bomb = Δt of the water, so:
− qrxn = qcal = [ HCcal Δt ] = + (cmΔtwater + HCΔtbomb )](https://image.slidesharecdn.com/all-chem-notes-130329135633-phpapp01/75/All-chem-notes-496-2048.jpg)



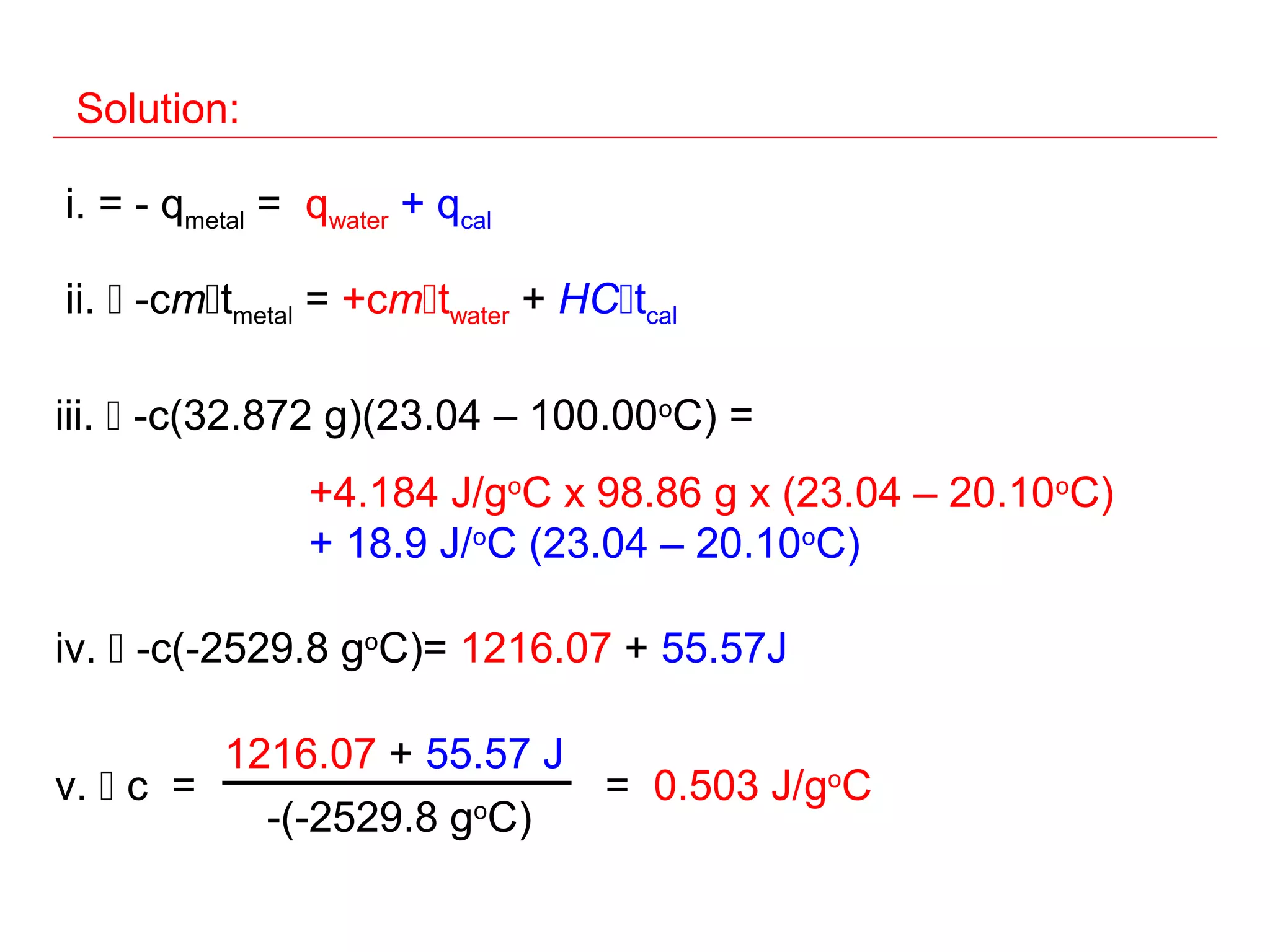
![Constant Pressure Calorimetry
Determining the specific
heat of a metal
qsys = qwater + qcal + qmetal
qsys = 0
- qmetal = + (qwater + qcal)
hot metal
where qwater = [ cm∆t ] H O
2
water
and qcal = HCcal x ∆tcal
-qmetal
finally: c (metal) =
mtmetal
No heat enters or leaves!](https://image.slidesharecdn.com/all-chem-notes-130329135633-phpapp01/75/All-chem-notes-500-2048.jpg)












![Hess’s Law
rxn A: CO (g) + ½ O2 (g) CO2 (g) HA = −283.0 kJ/ml
rxn B: ½ [2 NO (g) N2 (g) + O2 (g) ] HB = ½ (−180.6 kJ/mol)
reverse the sign of ΔH when you
reverse the reaction direction
net
rxn CO(g) + NO (g) CO2 (g) + ½ N2 (g)
net Hrxn :
ΔHA = − 283.0 kJ/mol
+ ΔHB = ½ (−180.6) kJ/mol
Hrxn = −373.3 kJ/mol](https://image.slidesharecdn.com/all-chem-notes-130329135633-phpapp01/75/All-chem-notes-514-2048.jpg)




![Standard Enthalpy of Reaction (Hºrxn )
The standard enthalpy of reaction (∆Hºrxn ) is the
enthalpy of a reaction in which reactants and
products are in their standard states at 1 atm.
aA + bB cC + dD
∆Hº = [ c∆Hºf (C) + d∆Hºf (D) ] - [ a∆Hfº (A) + b∆Hfº (B) ]
rxn
∆Hrxn = Σ n∆Hºf (products) - Σ m∆Hºf (reactants)
º
In order to use this equation, we must know Hºf values for each species.
If not already known, these must be calculated first.](https://image.slidesharecdn.com/all-chem-notes-130329135633-phpapp01/75/All-chem-notes-519-2048.jpg)
![Example: Benzene (C6H6) burns in air to produce carbon
dioxide and liquid water. How much heat is released per mole
of benzene combusted (i.e., determine Hºrxn) ? The standard
enthalpy of formation of benzene is 49.04 kJ/mol. See also
table 6.4.
2C6H6 (l) + 15O2 (g) 12CO2 (g) + 6H2O (l)
∆Hrxn = Σ n∆Hºf (products) - Σ m∆Hfº (reactants)
º
0
∆Hº rxn = [ 12∆Hºf (CO2) + 6∆Hºf (H2O) ] - [ 2∆Hºf (C6H6) + 15Hºf (O2)]
∆Hrxn = [ 12(–393.5) + 6(–187.6) ] – [ 2(49.04) ] = -5946 kJ
º
this is for 2
-5946 kJ
Hºrxn / mol = = - 2973 kJ/mol C6H6 mol C6H6
2 mol C6H6](https://image.slidesharecdn.com/all-chem-notes-130329135633-phpapp01/75/All-chem-notes-520-2048.jpg)
![Example: It is found, experimentally, that the production of
NH3 from its component elements releases 92.6 kJ,
according to the equation below. Calculate Hfº of NH3.
N2 (g) + 3 H 2 (g) 2 NH3 (g) Hrxnº = -92.6 kJ
Horxn = 2 Hfº(NH3, g) – [Hfº(N2, g) + 3 Hfº(H2 , g)]
But Hfº(N2, g) = 0 and Hfº(H2, g) = 0
Hºrxn = -92.6 kJ = 2 Hfº(NH3, g) – (0 + 0)
Hfº(NH3, g) = -92.6 kJ / 2 = -46.3 kJ/mol NH3](https://image.slidesharecdn.com/all-chem-notes-130329135633-phpapp01/75/All-chem-notes-521-2048.jpg)

























































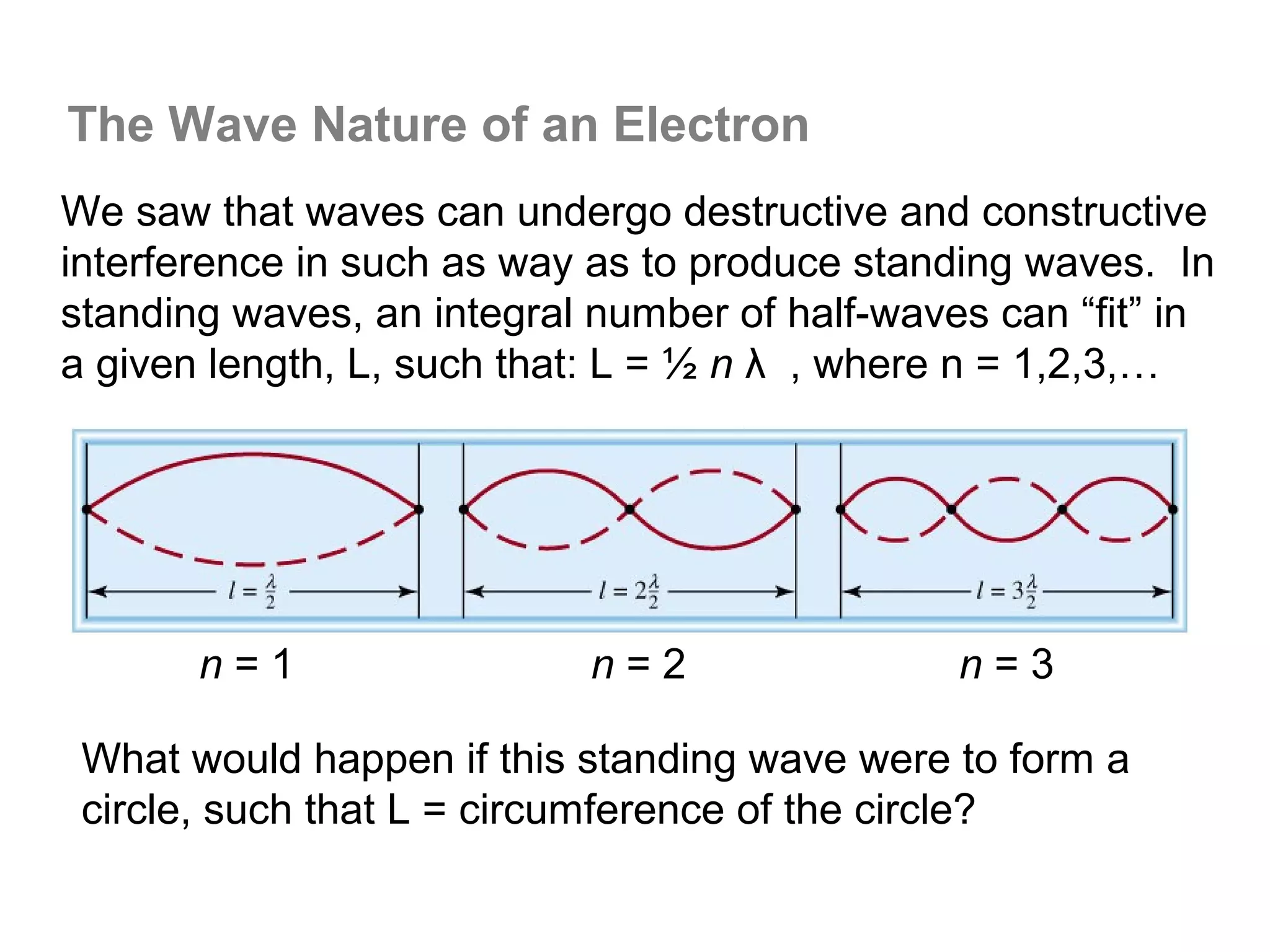

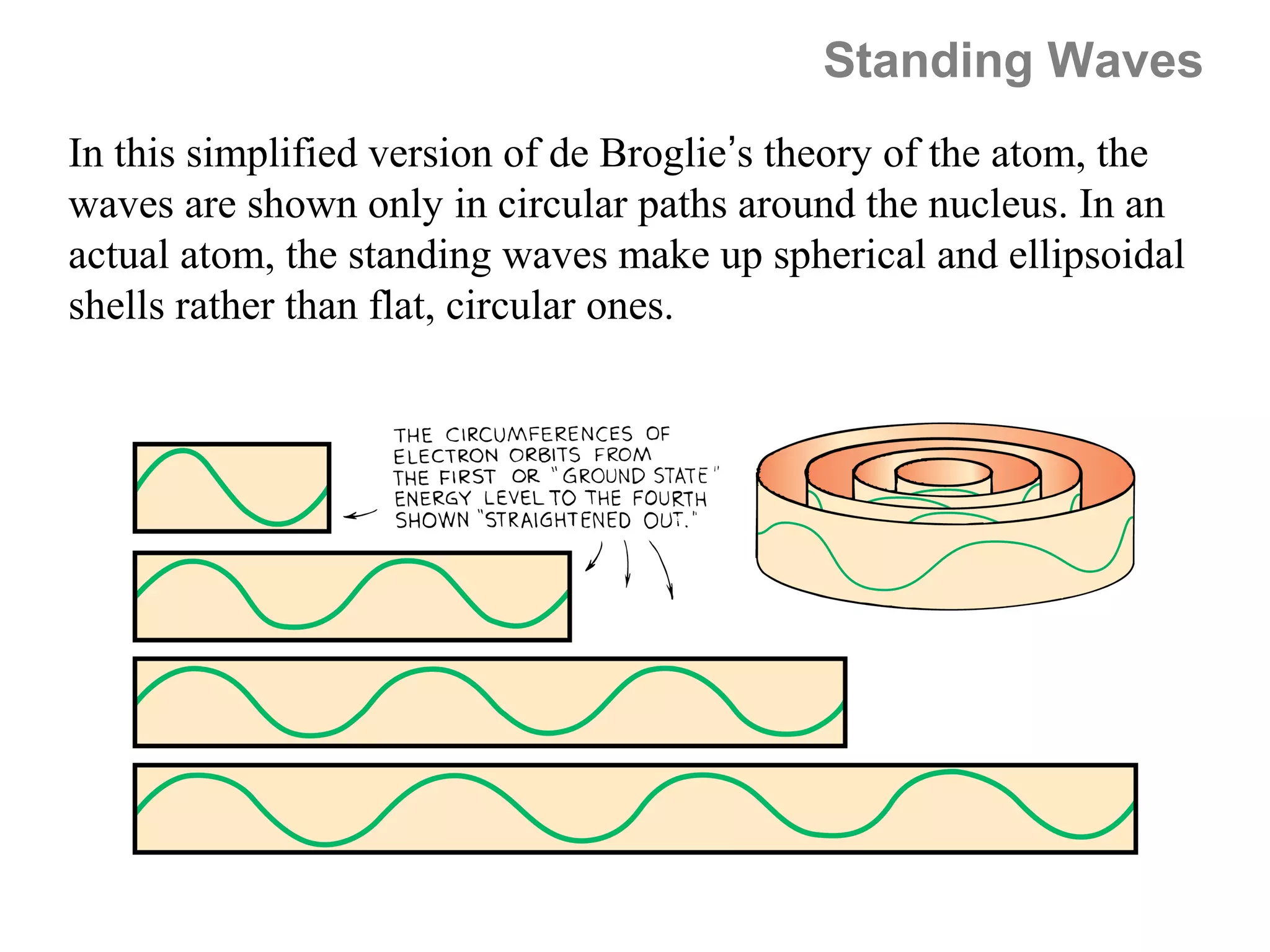

















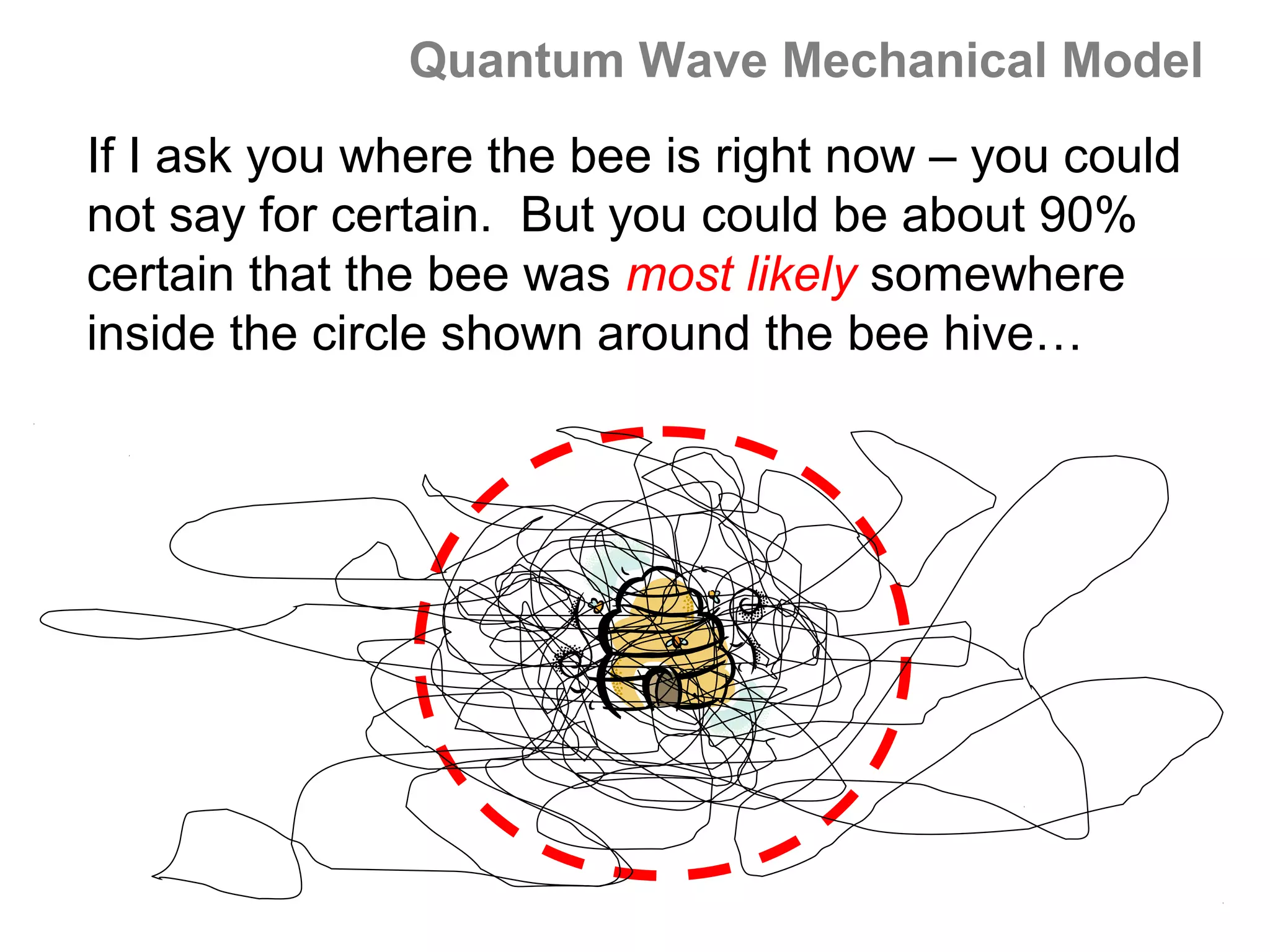








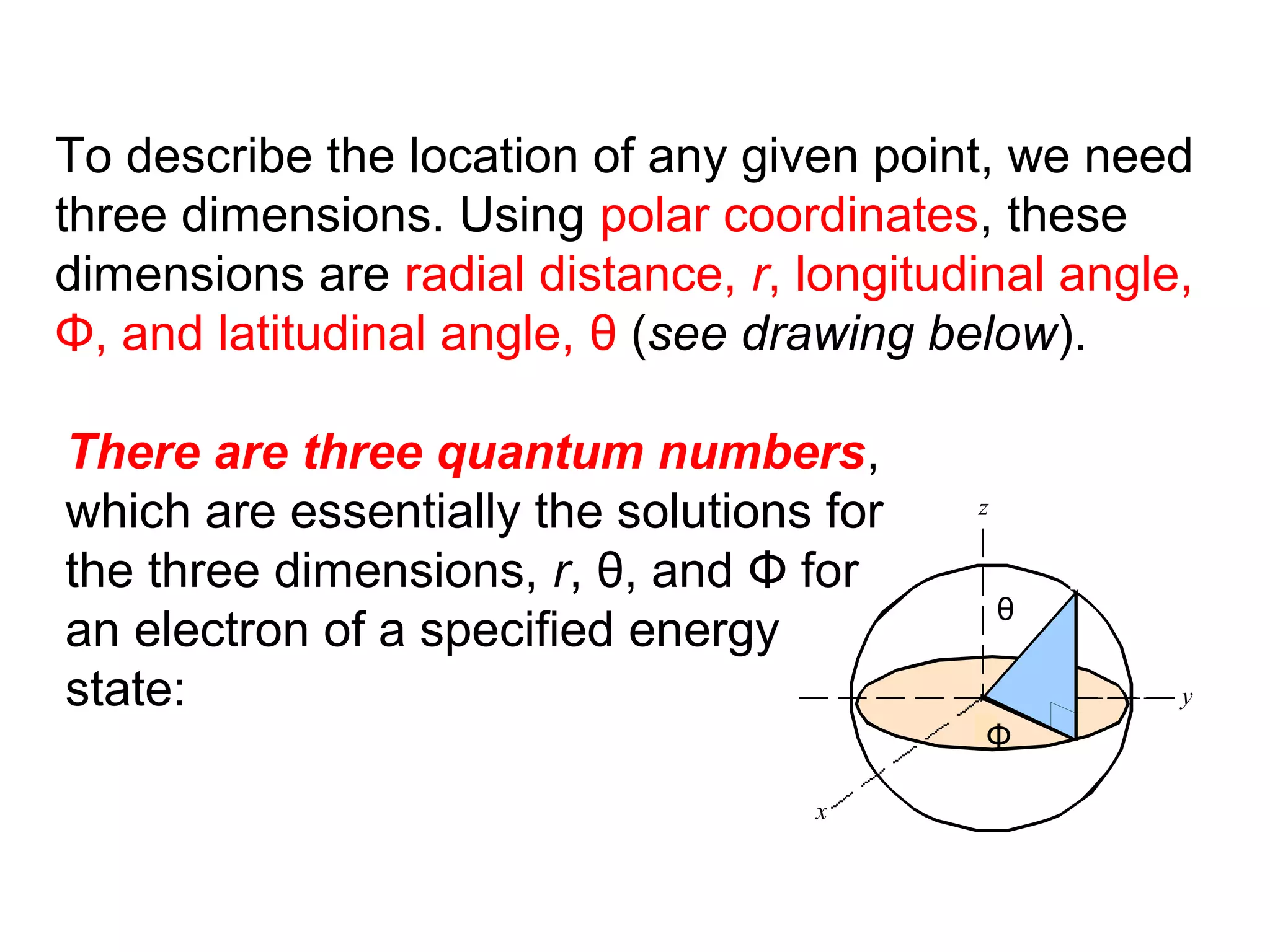







































![Isoelectronic series
Atoms and ions that have the same number of
electrons (hence, the same ground state electron
configuration) are said to be isoelectronic.
e.g.: Na+, Al3+, O2- and N3- all have a total of 10
electrons – that is, they all have the same electron
configuration as [Ne].
Example: what would be an isoelectronic series for elements
# 19 – 25?
K+ Ca2+ Sc3+ Ti4+ V5+ Cr6+ Mn7+ = [Ar]](https://image.slidesharecdn.com/all-chem-notes-130329135633-phpapp01/75/All-chem-notes-659-2048.jpg)



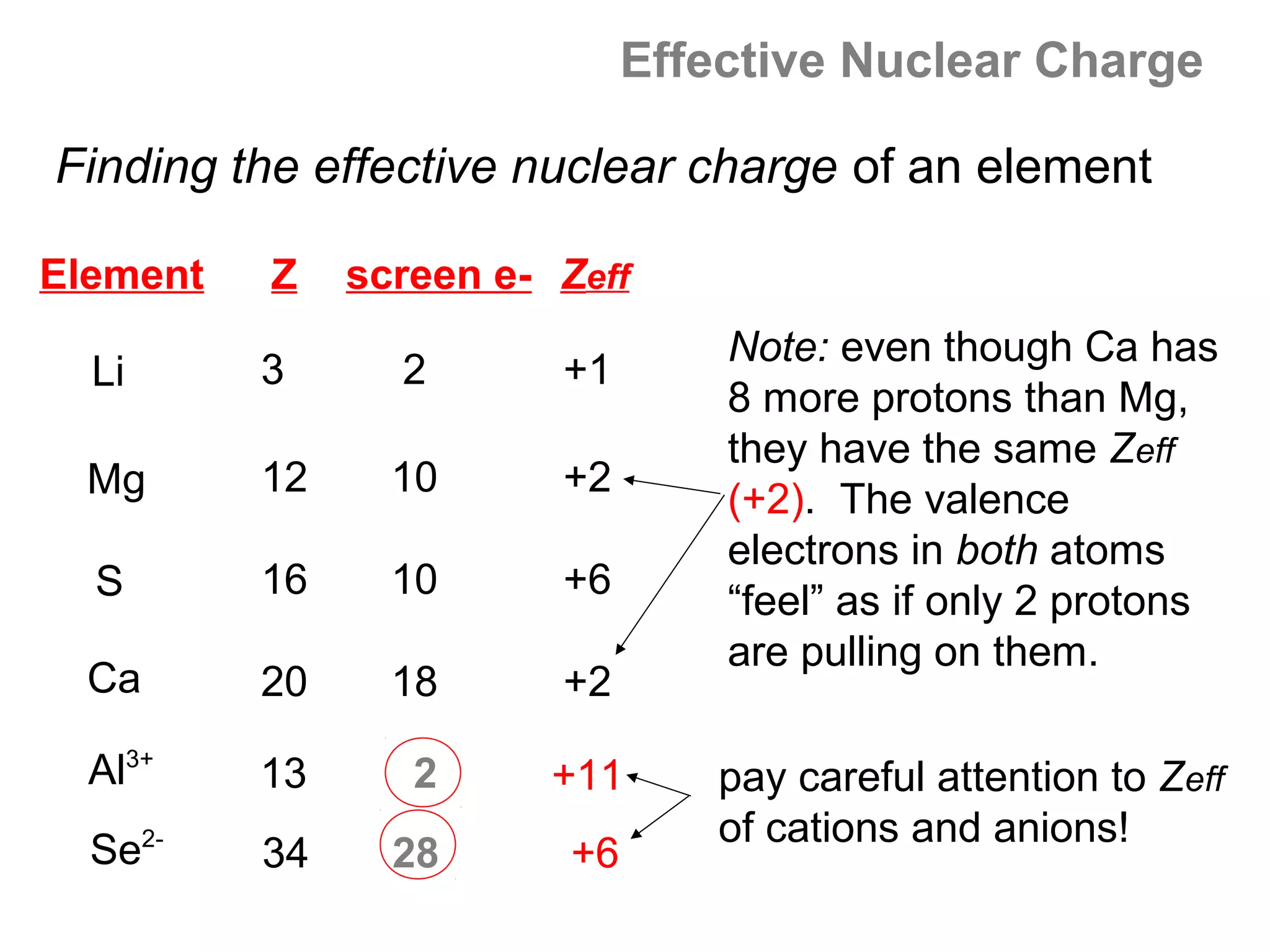


![Effective Nuclear Charge
Trends in Zeff : Across a period
Na (Z = 11) Al (Z = 13) P (Z =15) Cl (Z = 17)
[Ne]3s1 [Ne]3s23p1 [Ne]3s23p3 [Ne]3s23p5
As you move across a period, the number of protons
(Z) increases steadily. The added electrons are
entering the same shell, so the number of interior
shell screening electrons does not change.](https://image.slidesharecdn.com/all-chem-notes-130329135633-phpapp01/75/All-chem-notes-666-2048.jpg)













![Size of Ions
Explanation: Size of the cation
A cation is formed when an atom loses valence
electrons. When an atom loses its valence electrons,
it tends to lose the entire valence shell – so the
cation is much smaller than the original atom.
Note also that the
When this 3 shell
rd
Zeff acting on the
e- is removed… +
remaining valence
shell electrons is
now (11-2) = +9,
…only the 2 inner so the 2nd shell is
shells remain pulled inward,
making the cation
Na : [Ne]3s1 even smaller.
Na+ : [Ne] 3s0](https://image.slidesharecdn.com/all-chem-notes-130329135633-phpapp01/75/All-chem-notes-681-2048.jpg)







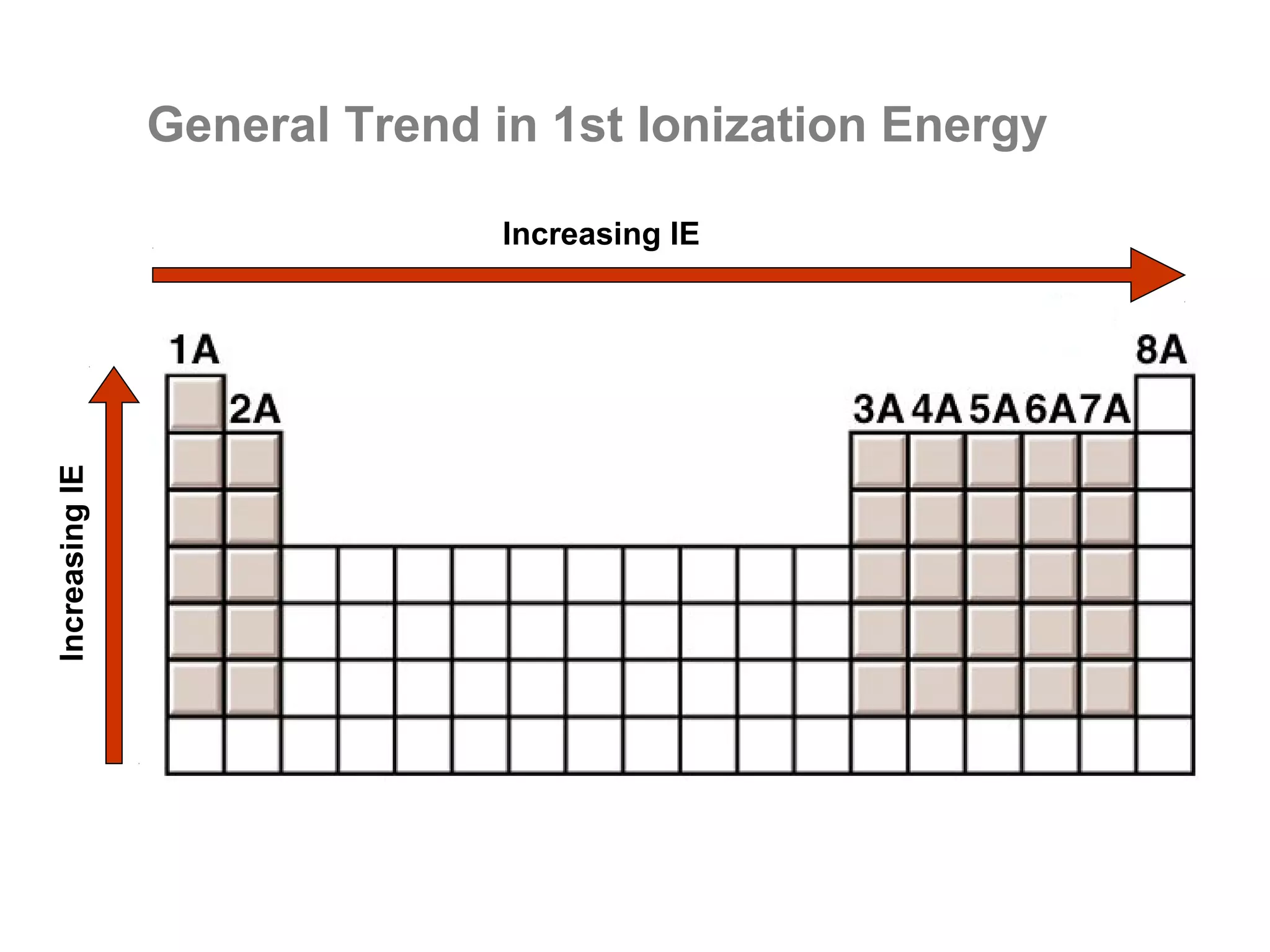









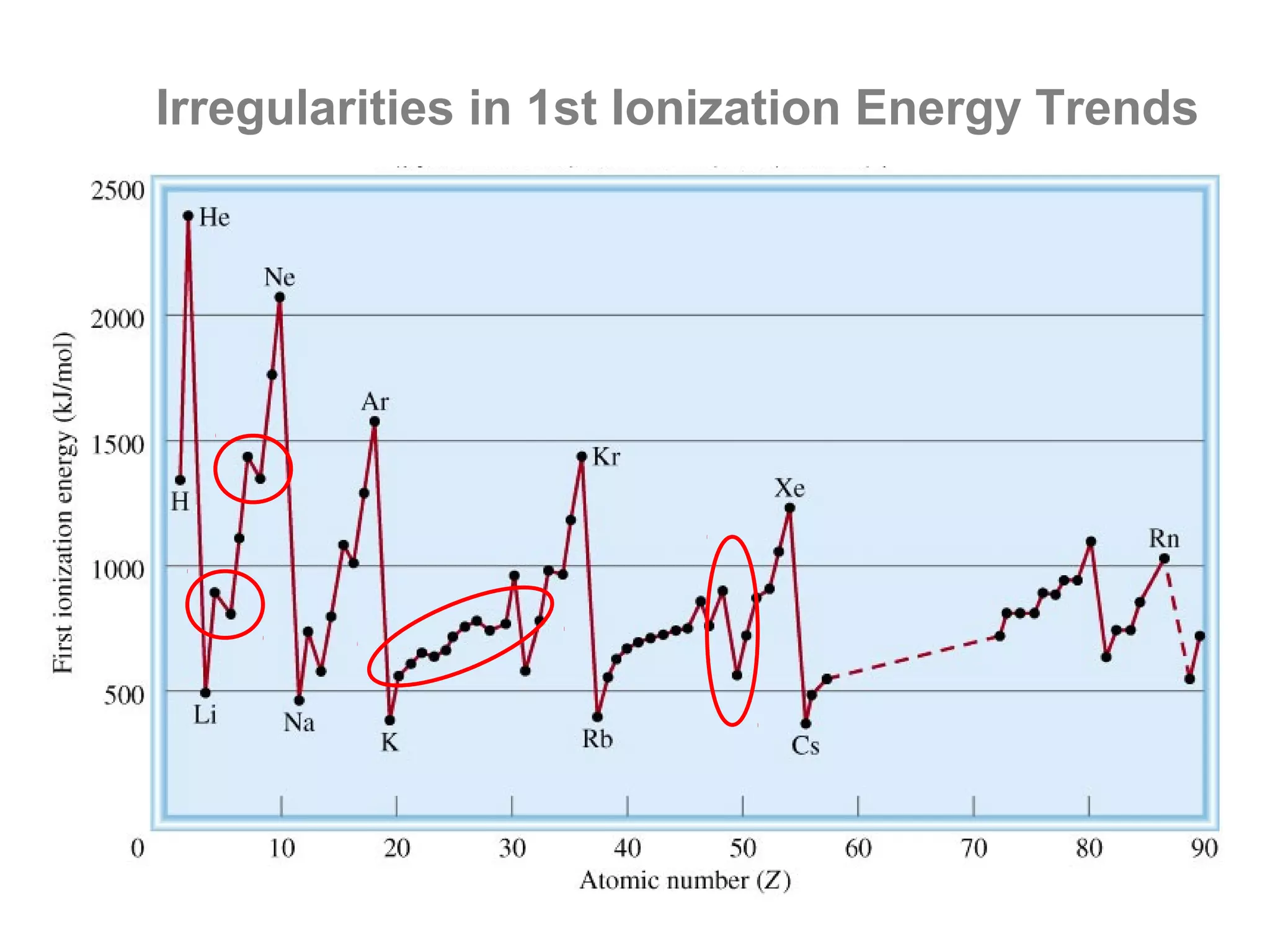

![Multiple Ionization Energies
Removing an electron may leave the atom with a filled or
half-filled subshell. Removing the next electron will require
a somewhat larger than expected jump in energy, due to
the special stability of such filled and exactly half-filled
subshells.
Example: consider the successive IE for oxygen:
O O+ O2+ O3+ O4+ O5+
[He]2s22p4 [He]2s22p3 [He]2s22p2 [He]2s22p1 [He]2s2 [He]2s1
1,314 3,390 5,300 7,470 11,000 13,000
increase: +2,076 +1,910 +2,170 +3,530 +2,000](https://image.slidesharecdn.com/all-chem-notes-130329135633-phpapp01/75/All-chem-notes-701-2048.jpg)
![Multiple Ionization Energies
If removing an electron leaves the atom with a noble gas
core (s2p6 valence configuration) then removing the next
electron will require a much larger jump in energy, since a
noble gas core electron configuration is the most stable
possible configuration.
Compare the first four ionization energies for Na and Al:
2nd IE
1 IE
st
(kJ/mol) 3rd IE (kJ/mol) 4th IE (kJ/mol)
(kJ/mol)
Na [Ne]2s1 [Ne] [He]2s22p5 [He]2s22p4
496 4,560 6,900 9,540
Al [Ne]2s22p1 [Ne]2s2 [Ne]2s1 [Ne]
578 1,820 2,750 11,600](https://image.slidesharecdn.com/all-chem-notes-130329135633-phpapp01/75/All-chem-notes-702-2048.jpg)










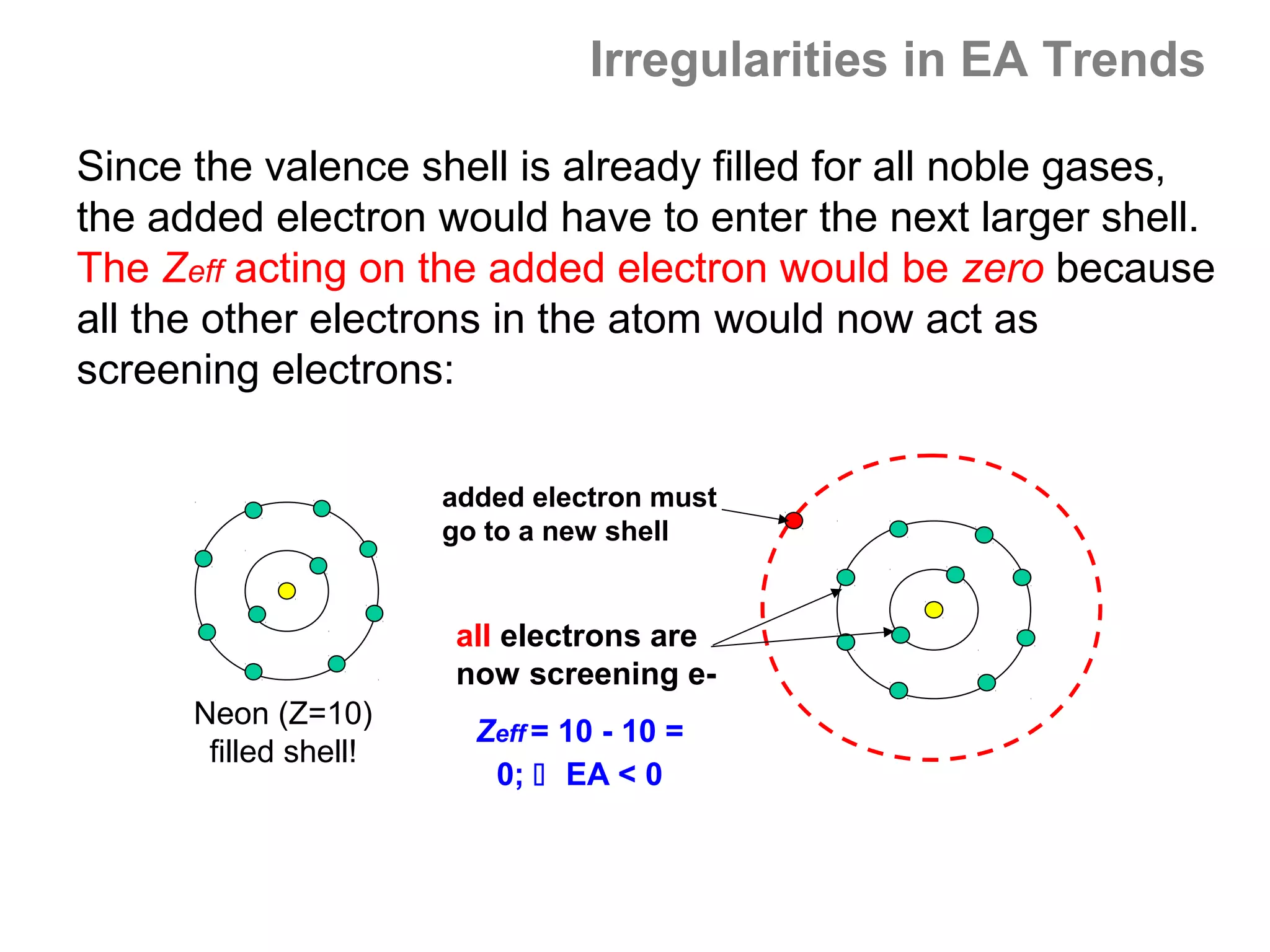
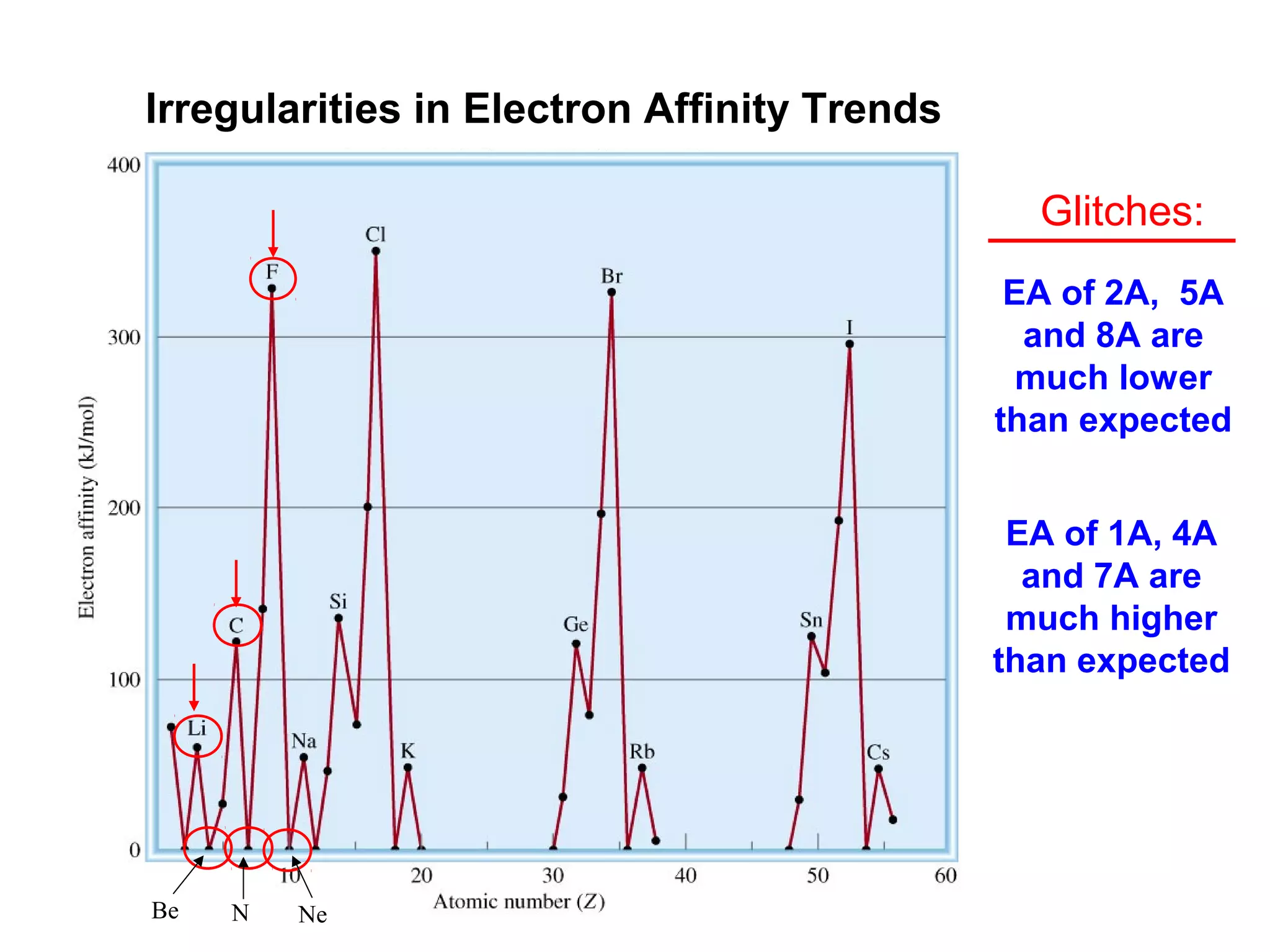





















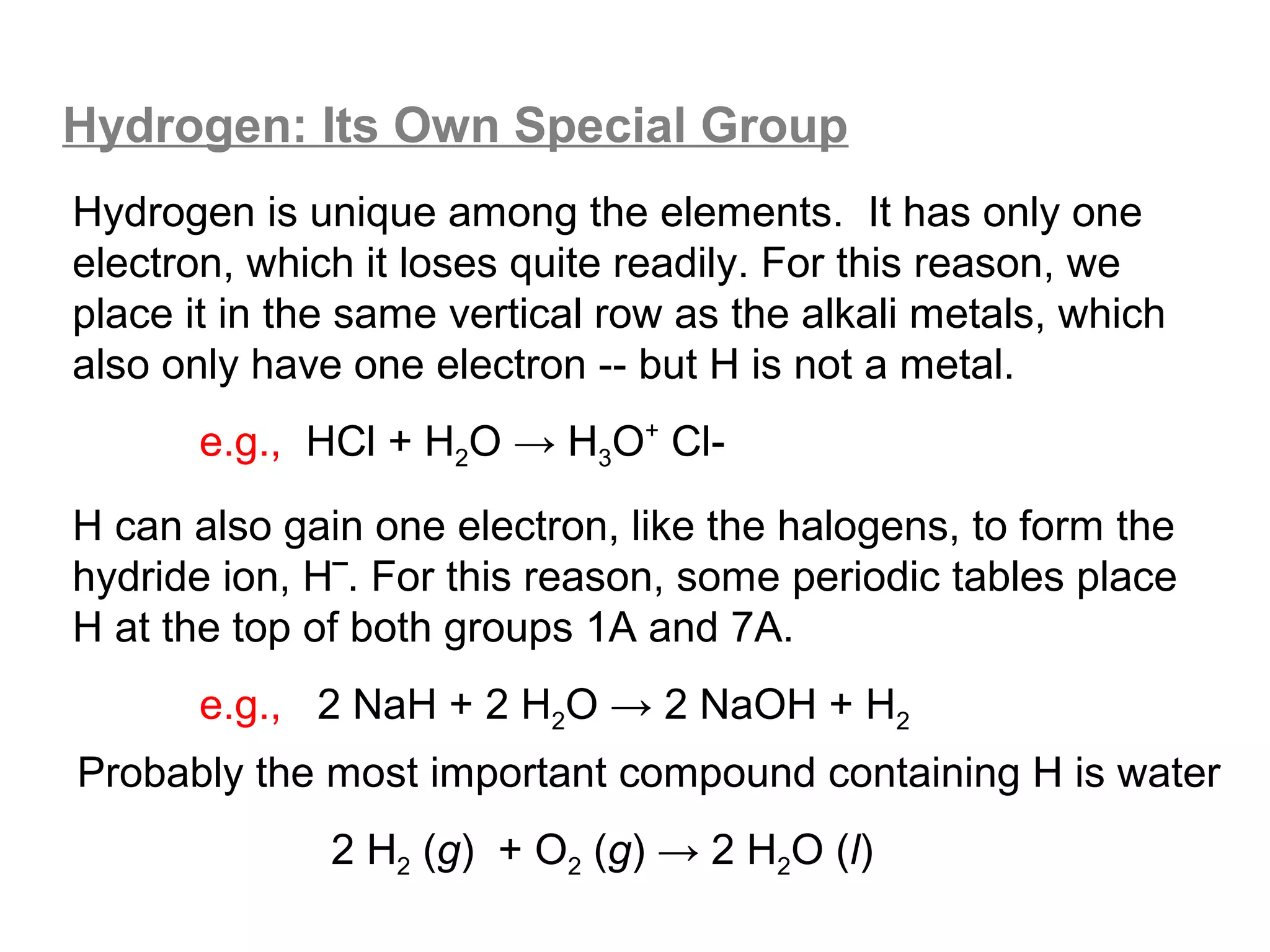

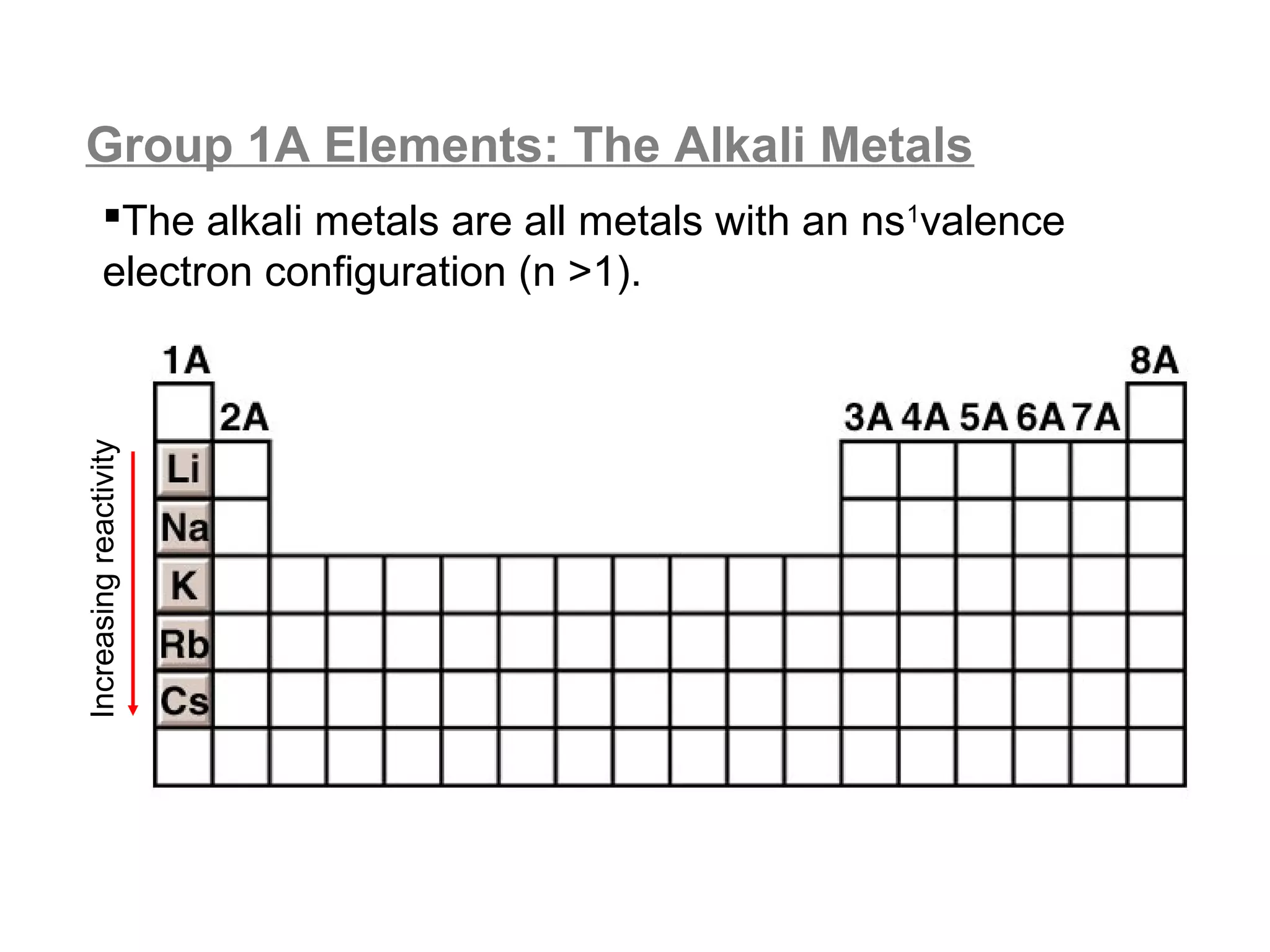





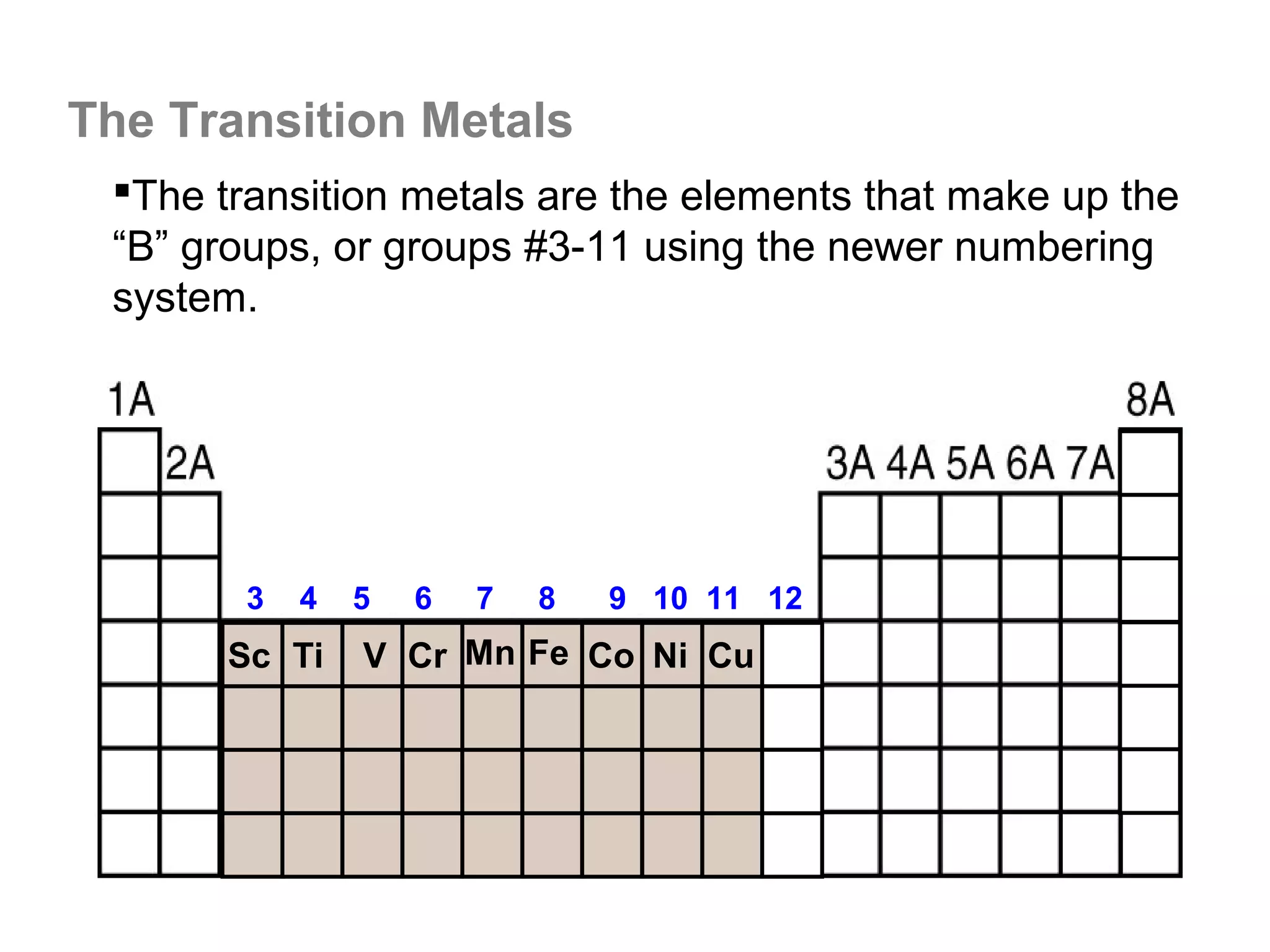




![A Comparison of Group A and Group B metals
Consider the electron configurations of Groups 1A and
Groups 2A with their B group counterparts (groups 11,12):
Group number electron configuration
group 1A metals [noble] ns1
group 1B (11) metals [noble] (n-1)d10ns1
group 2A metals [noble] ns2
group 2B (12) metals [noble] (n-1)d10ns2
Note that the A groups and B groups differ only in the
presence or absence of a filled d-subshell of electrons.](https://image.slidesharecdn.com/all-chem-notes-130329135633-phpapp01/75/All-chem-notes-751-2048.jpg)






































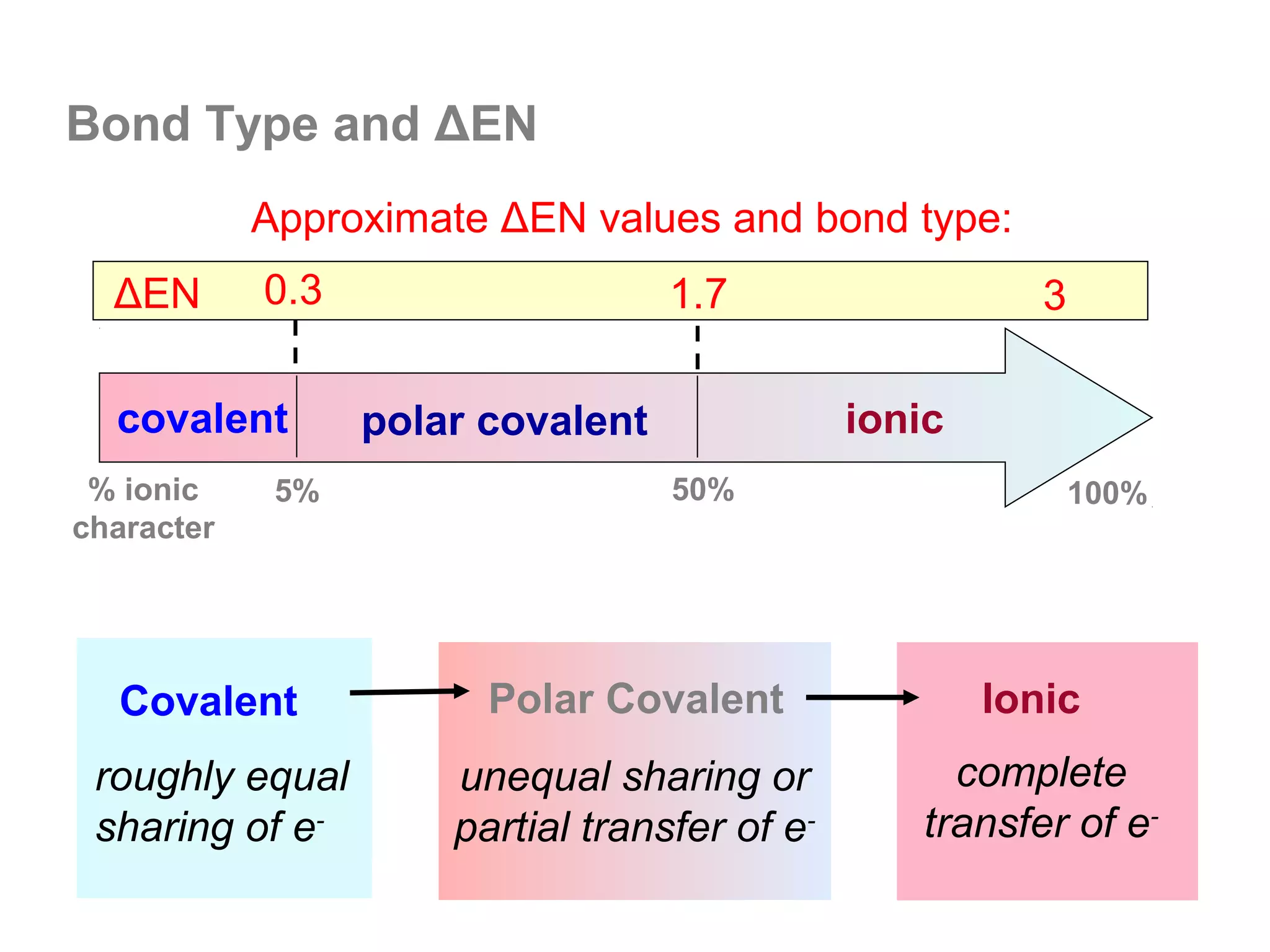






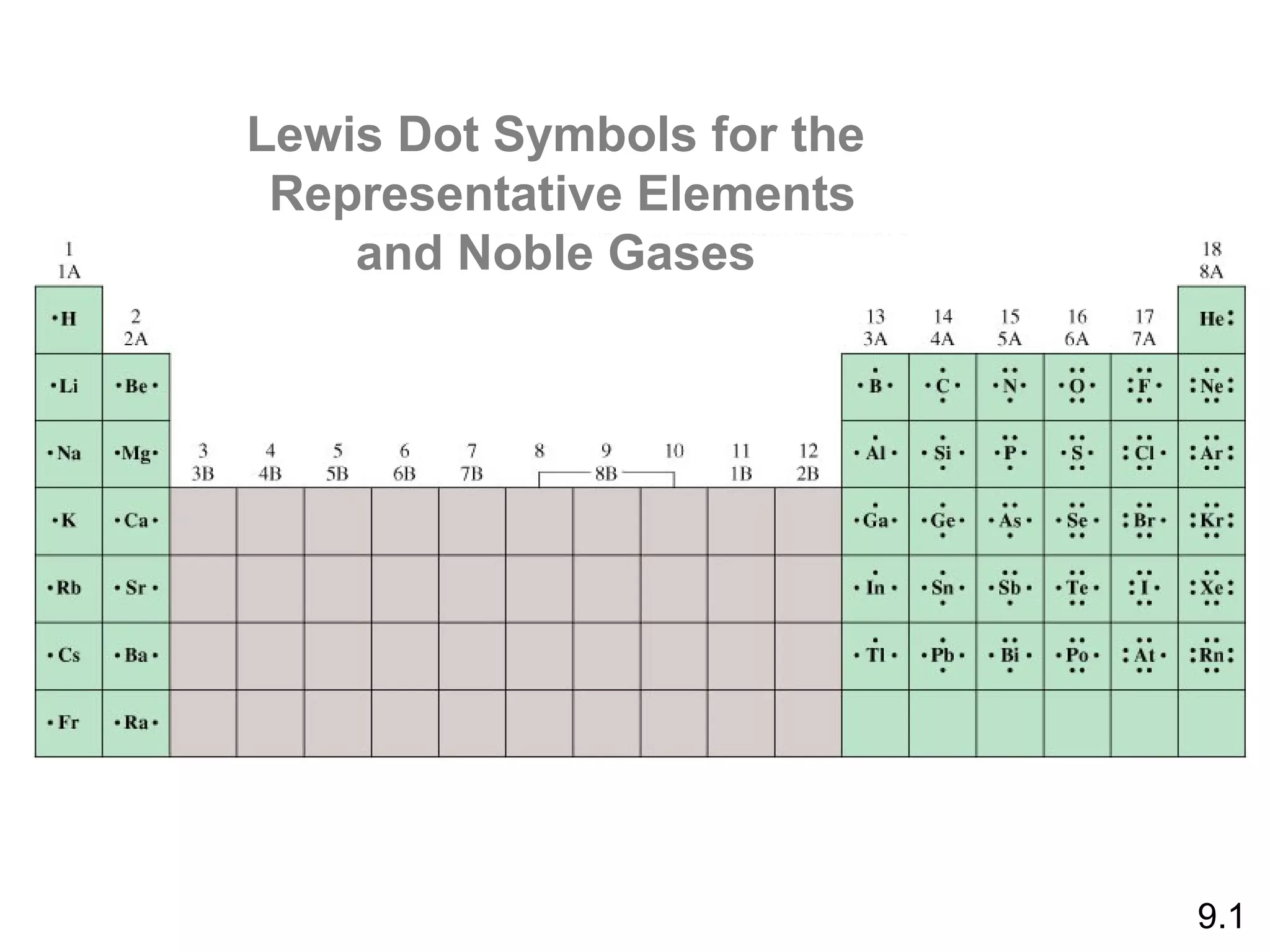
![Lewis Dot Symbols
We can represent the ionic bond that forms between
two atoms using Lewis dot symbols, as follows:
Li + F Li F 1s22s22p6 = [Ne]
1s22s1 1s22s22p5 1s2 = [He]
We often use a curved arrow to depict shifts
in the e- during reactions. The arrow always
points in the direction of e- movement.](https://image.slidesharecdn.com/all-chem-notes-130329135633-phpapp01/75/All-chem-notes-799-2048.jpg)






![The Born-Haber Cycle
By Hess’s Law, we have:
ΔHº1 + ΔHº2 + ΔHº3 + ΔHº4 + ΔHº5 = ΔH°f
Solving for ΔHº5 = lattice energy (U) , we obtain:
ΔH5 = U = ΔH°f − (ΔHº1 + ΔHº2 + ΔHº3 + ΔHº4 )
U = −594.1 −[(155 + 75 + 520 + (−328)] kJ/mol
U = −594 − (422) = −1016 kJ/mol LiF
That is, −1016 kJ of heat energy is released in forming 1.0
mole of LiF from its component ions (or +1016 kJ of energy
are needed to separate 1 mole of LiF into its gaseous ions).](https://image.slidesharecdn.com/all-chem-notes-130329135633-phpapp01/75/All-chem-notes-807-2048.jpg)




![Lattice Energy
By the same token, Na does not form Na2+ ions in
its compounds – the gain in lattice energy is not
sufficient to make up the difference for the huge
increase in ionization energy required to remove
the second electron from the stable [Ne] electron
configuration of the Na+ ion.
What is true about the cations also holds for the
anions: there is a trade off in the (-) EA of forming
higher charged anions (eg, F3−) vs the lattice energy
released when such higher charged ions combine to
form compounds.](https://image.slidesharecdn.com/all-chem-notes-130329135633-phpapp01/75/All-chem-notes-813-2048.jpg)




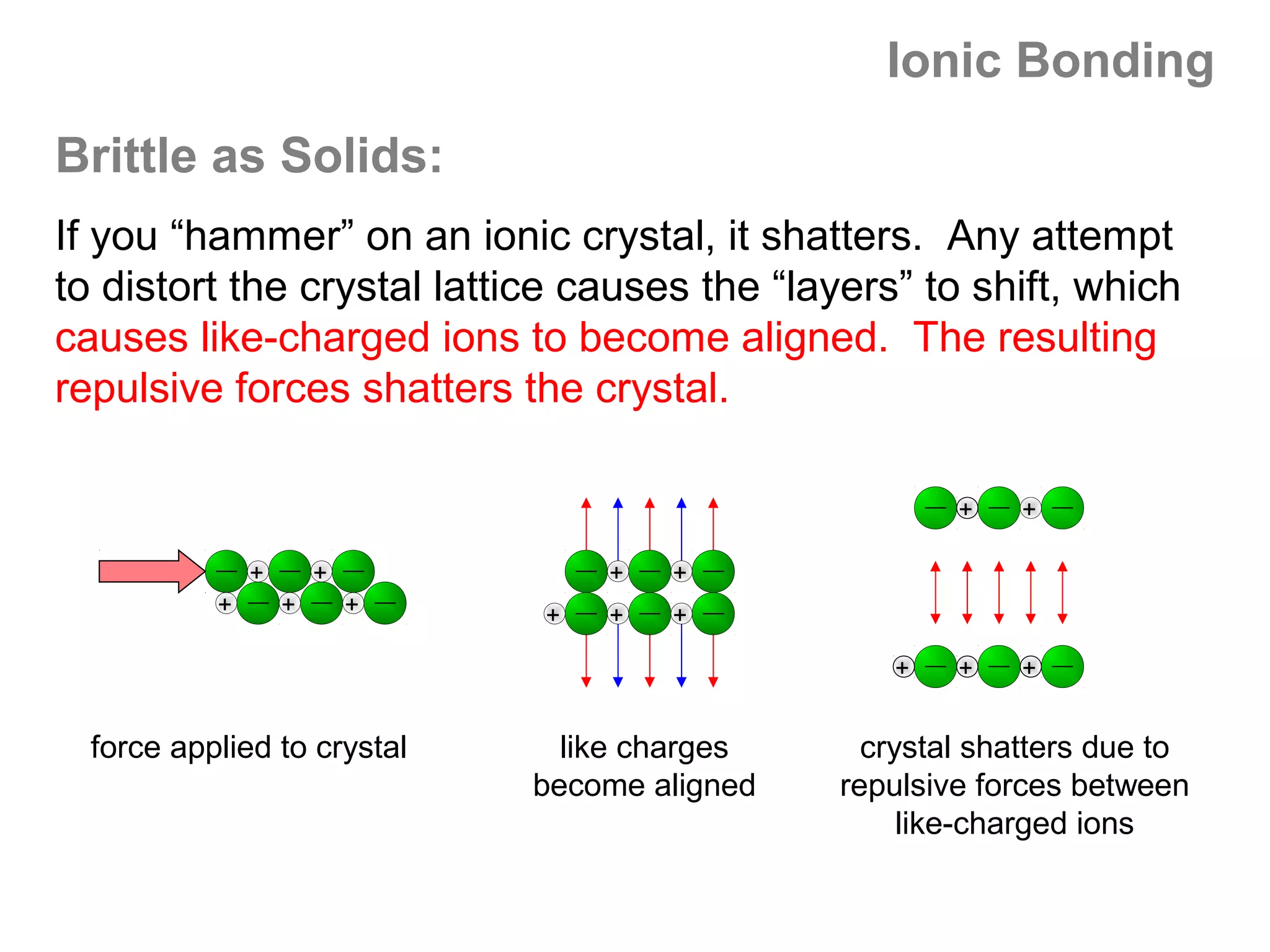






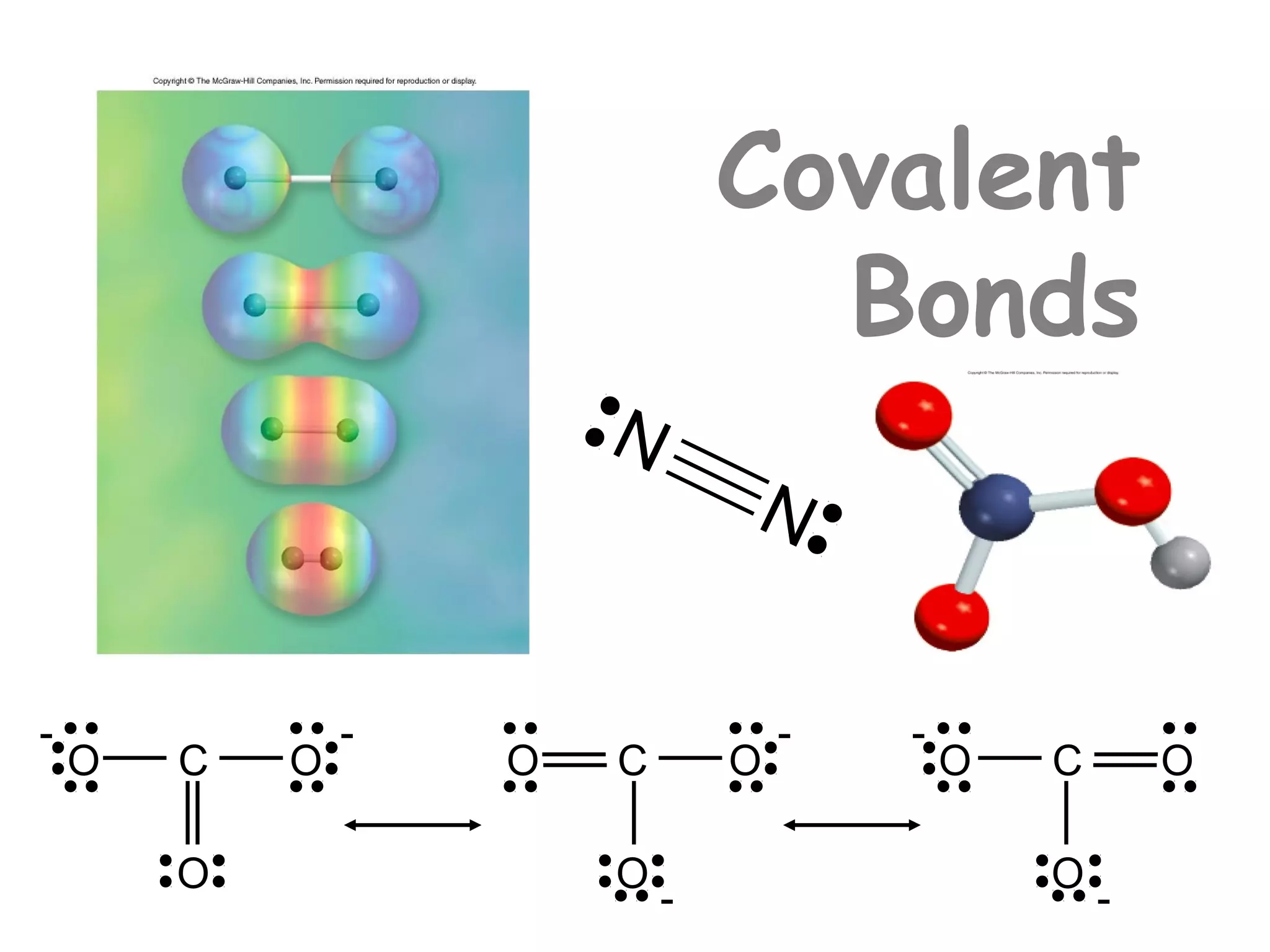



























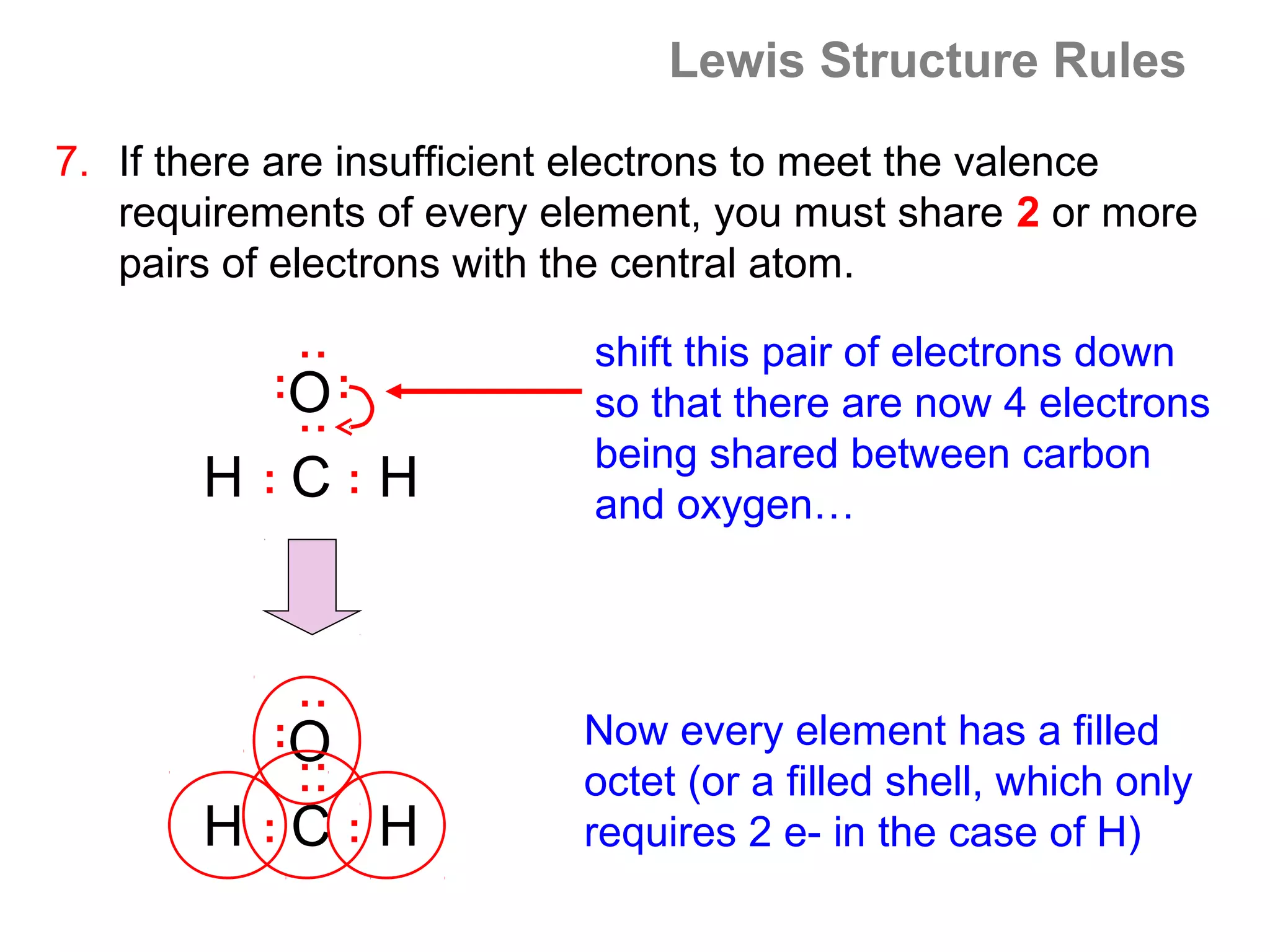


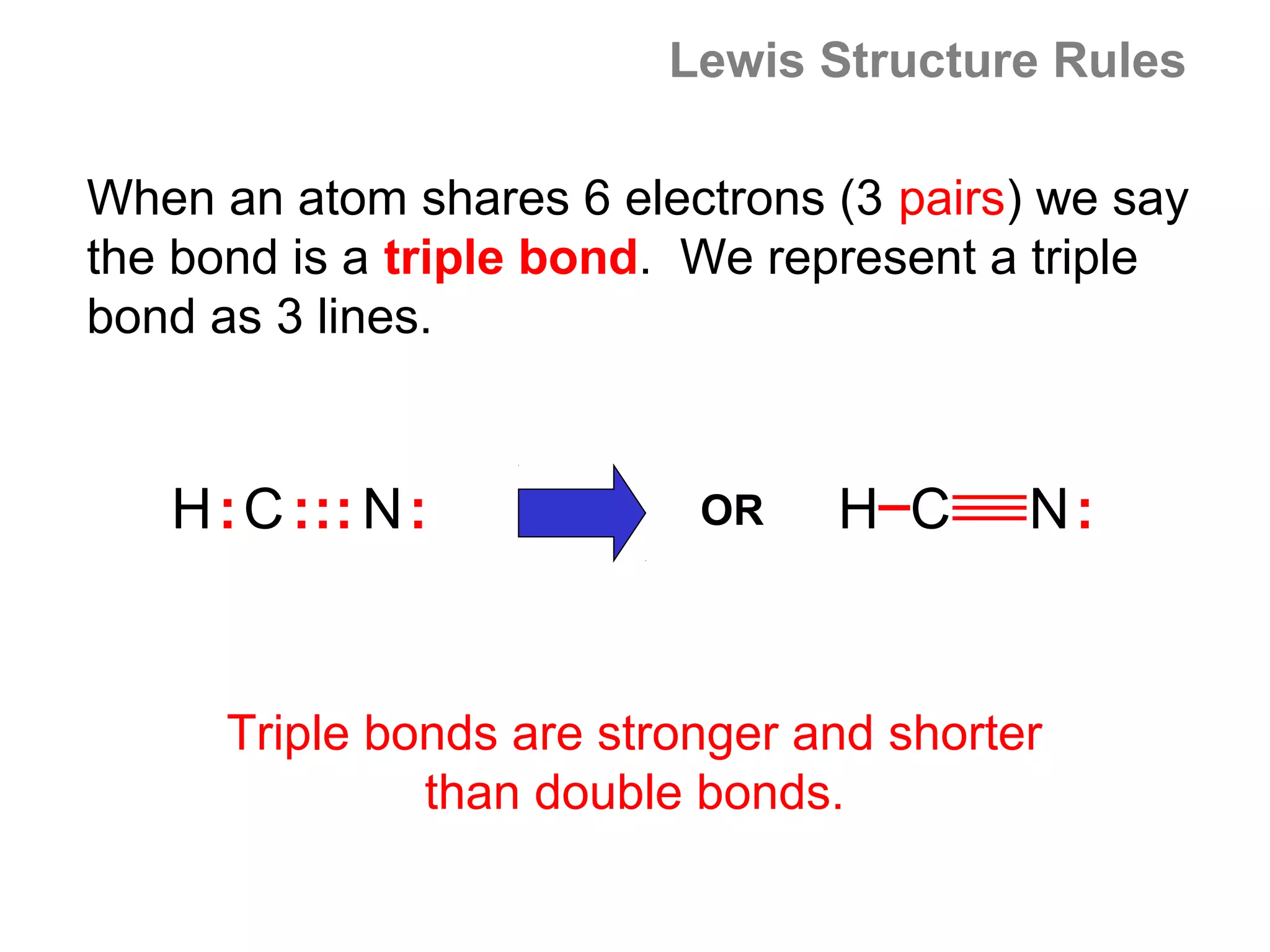


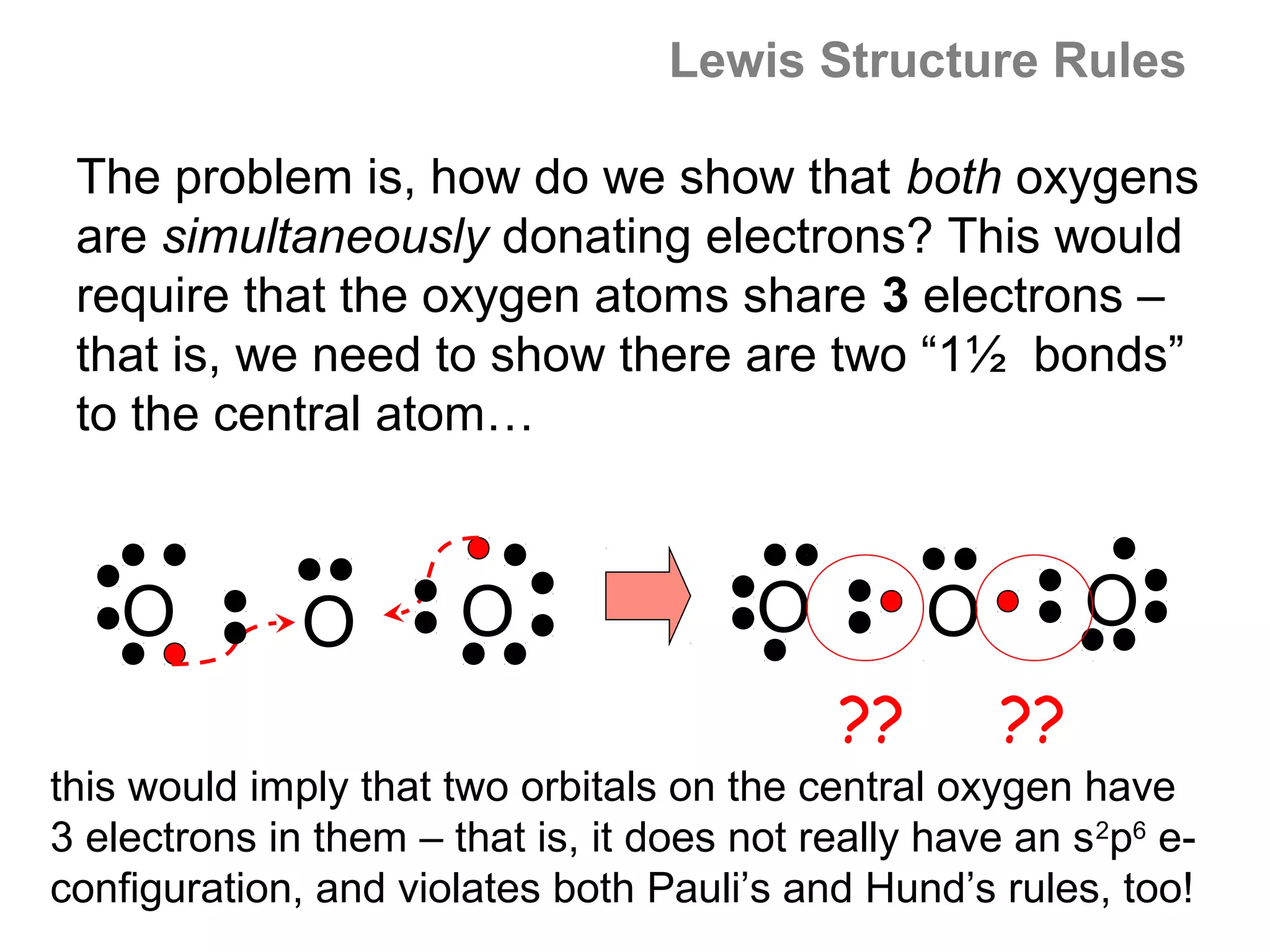
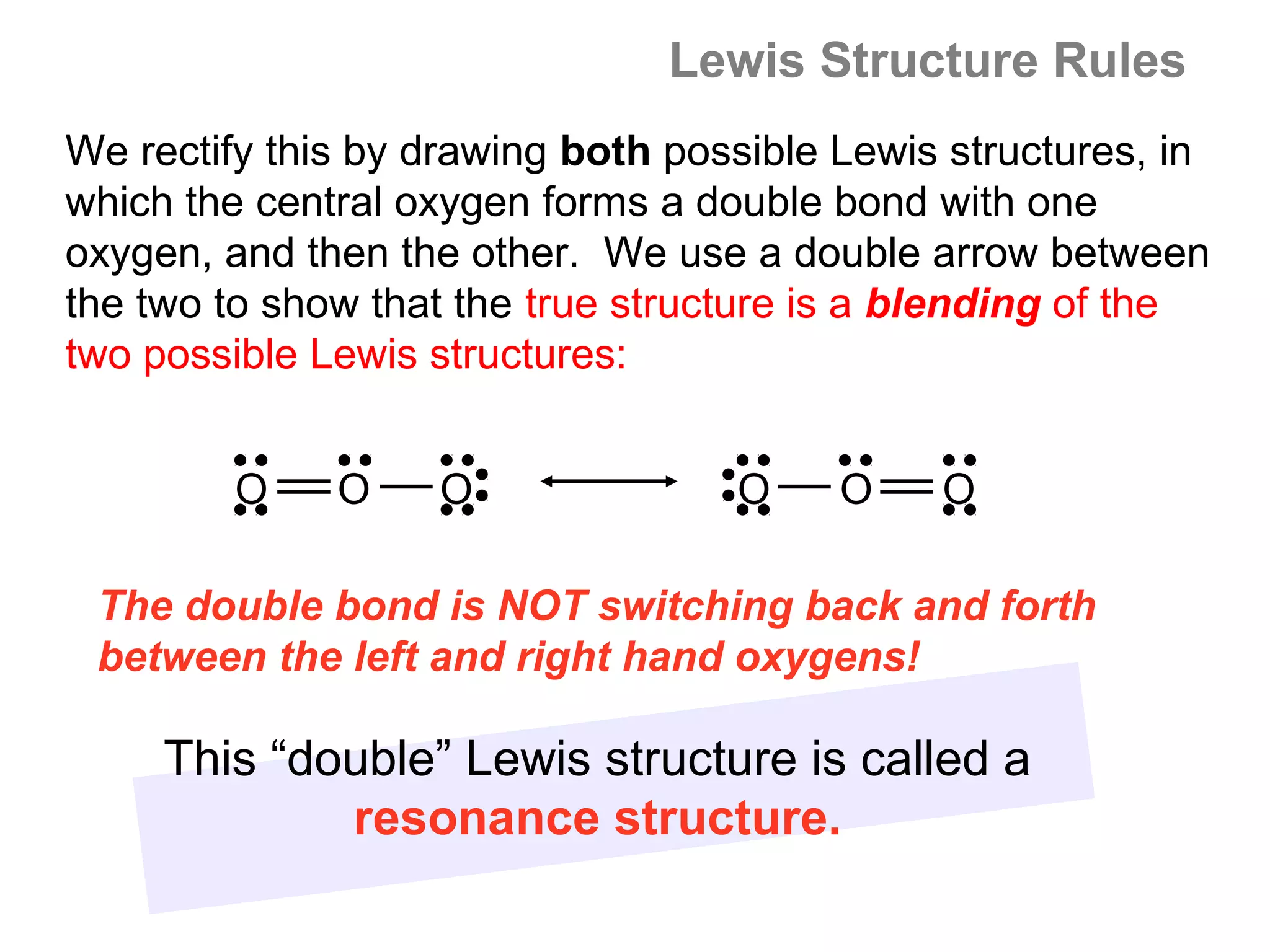


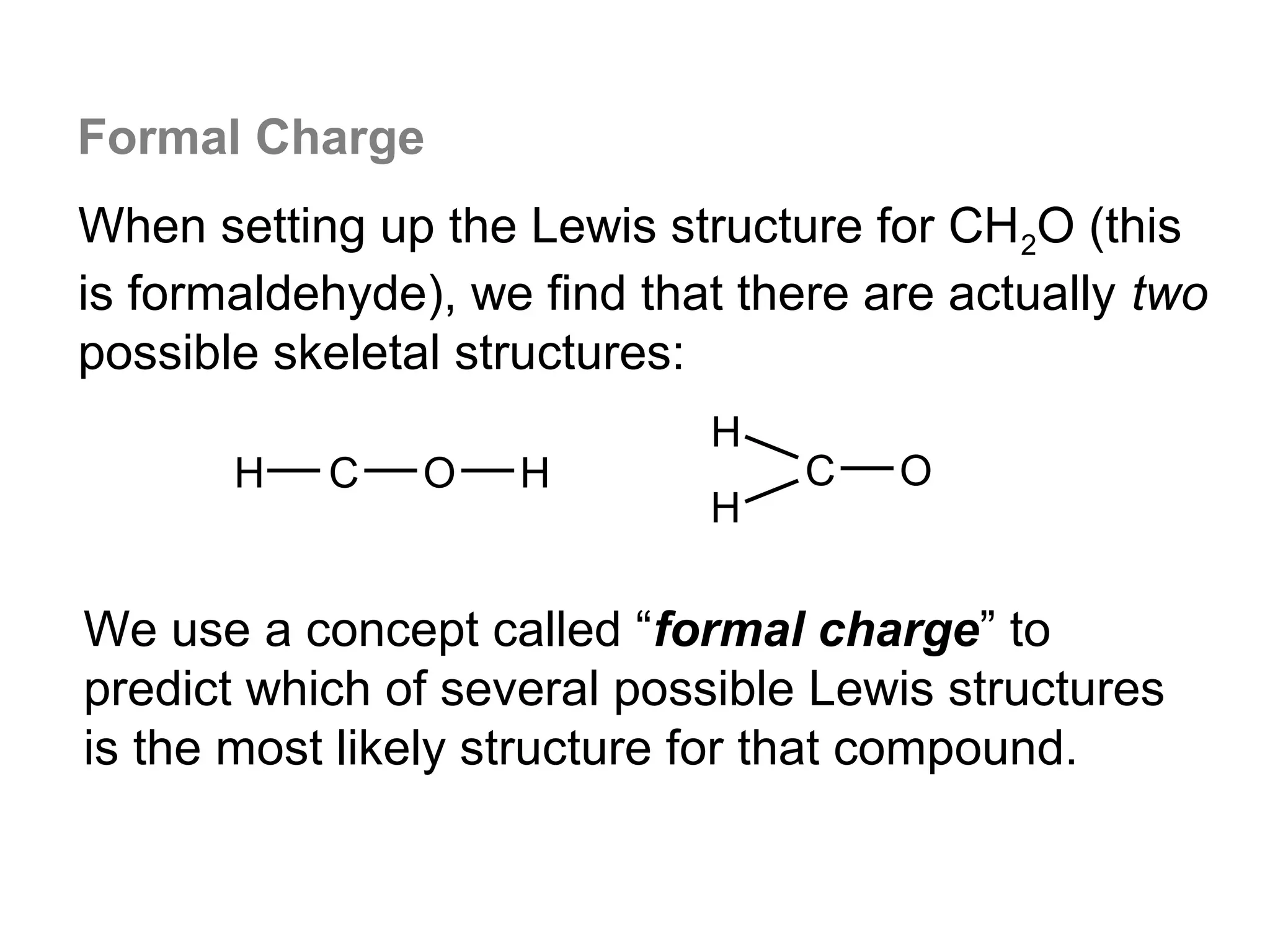

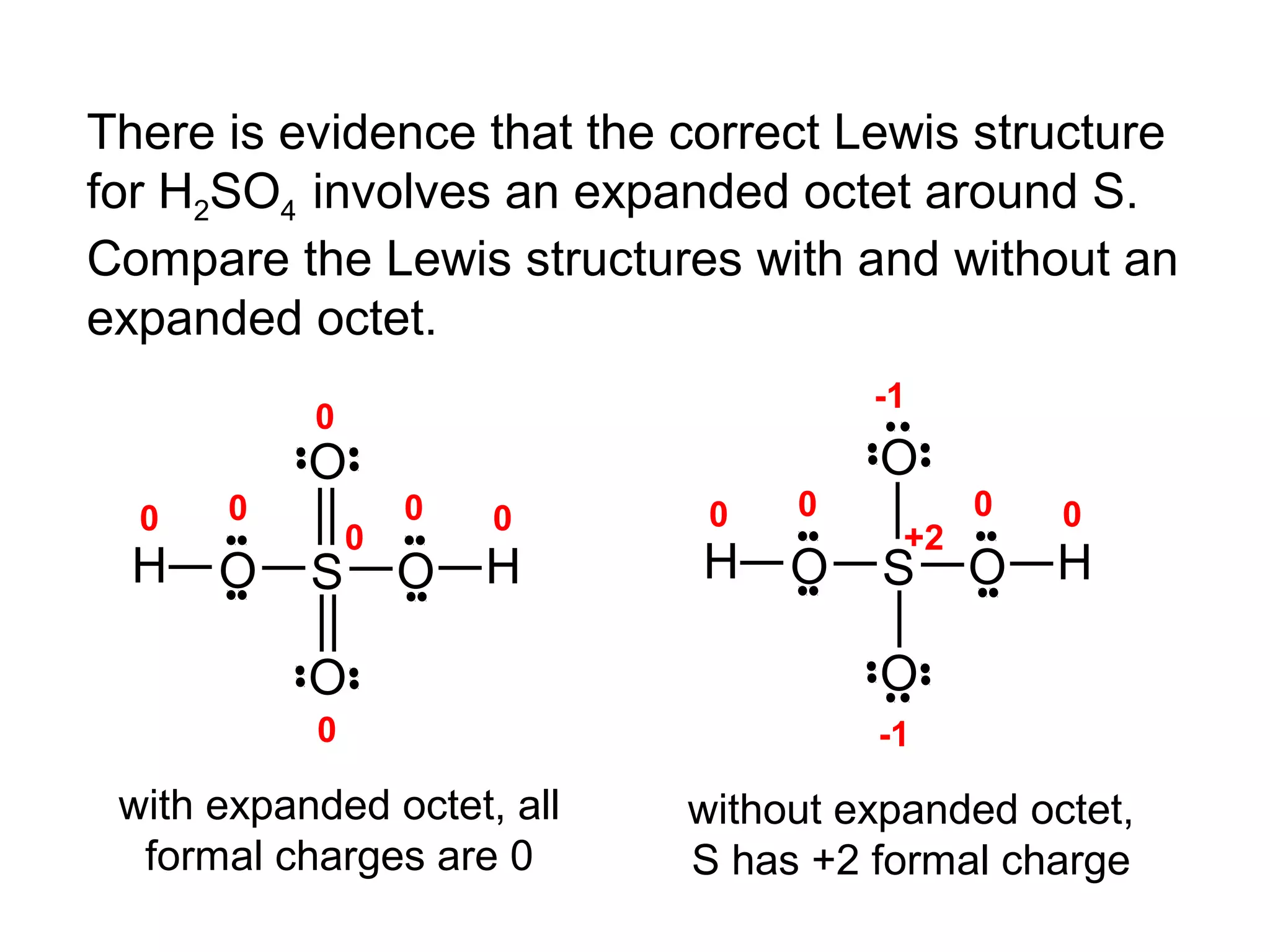
![Formal Charge
Example: What is the formal charge on the possible CH2O
structure shown below?
-1 +1
H C O H
formal charge total number
total number 1 total number
on an atom in
a Lewis
structure
of valence
= electrons in
the free atom
- of nonbonding
electrons
+ 2 ( of bonding
electrons )
formal charge
on Carbon
= 4 -[ 2 + ½ x 6 ] = -1
formal charge
Σ charge = 0
on Oxygen
= 6 - [ 2 + ½ x 6 ] = +1](https://image.slidesharecdn.com/all-chem-notes-130329135633-phpapp01/75/All-chem-notes-870-2048.jpg)
![Formal Charge
Example: What is the formal charge on the possible CH2O
structure shown below?
H 0 0
C O
H
formal charge total number
total number 1 total number
on an atom in
a Lewis
structure
of valence
= electrons in
the free atom
- of nonbonding
electrons
+ 2 ( of bonding
electrons )
formal charge
on Carbon
=4- [0 +½x8]=0
Σ charge = 0
formal charge
on Oxygen
=6- [4+½x4]=0](https://image.slidesharecdn.com/all-chem-notes-130329135633-phpapp01/75/All-chem-notes-871-2048.jpg)