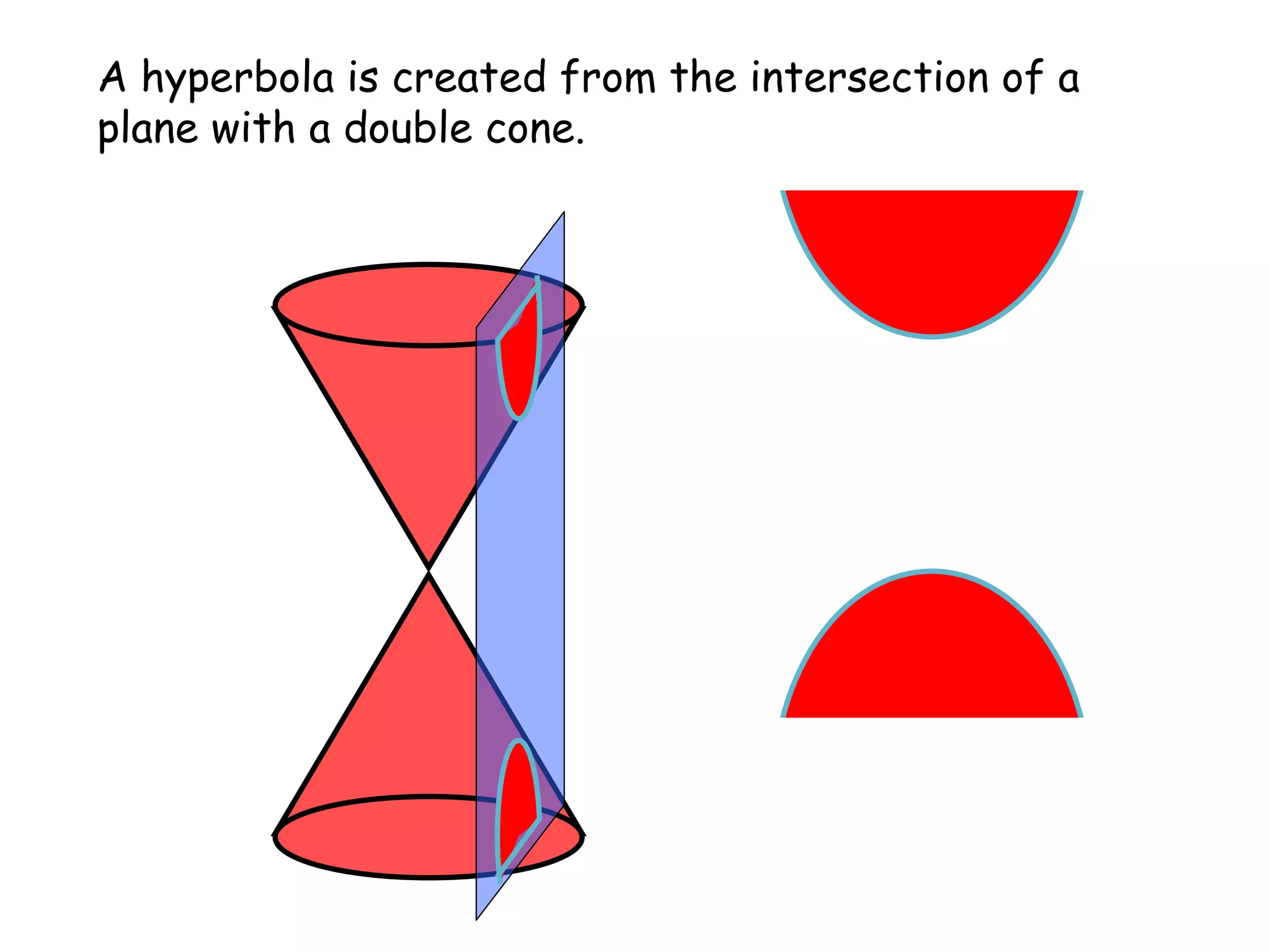
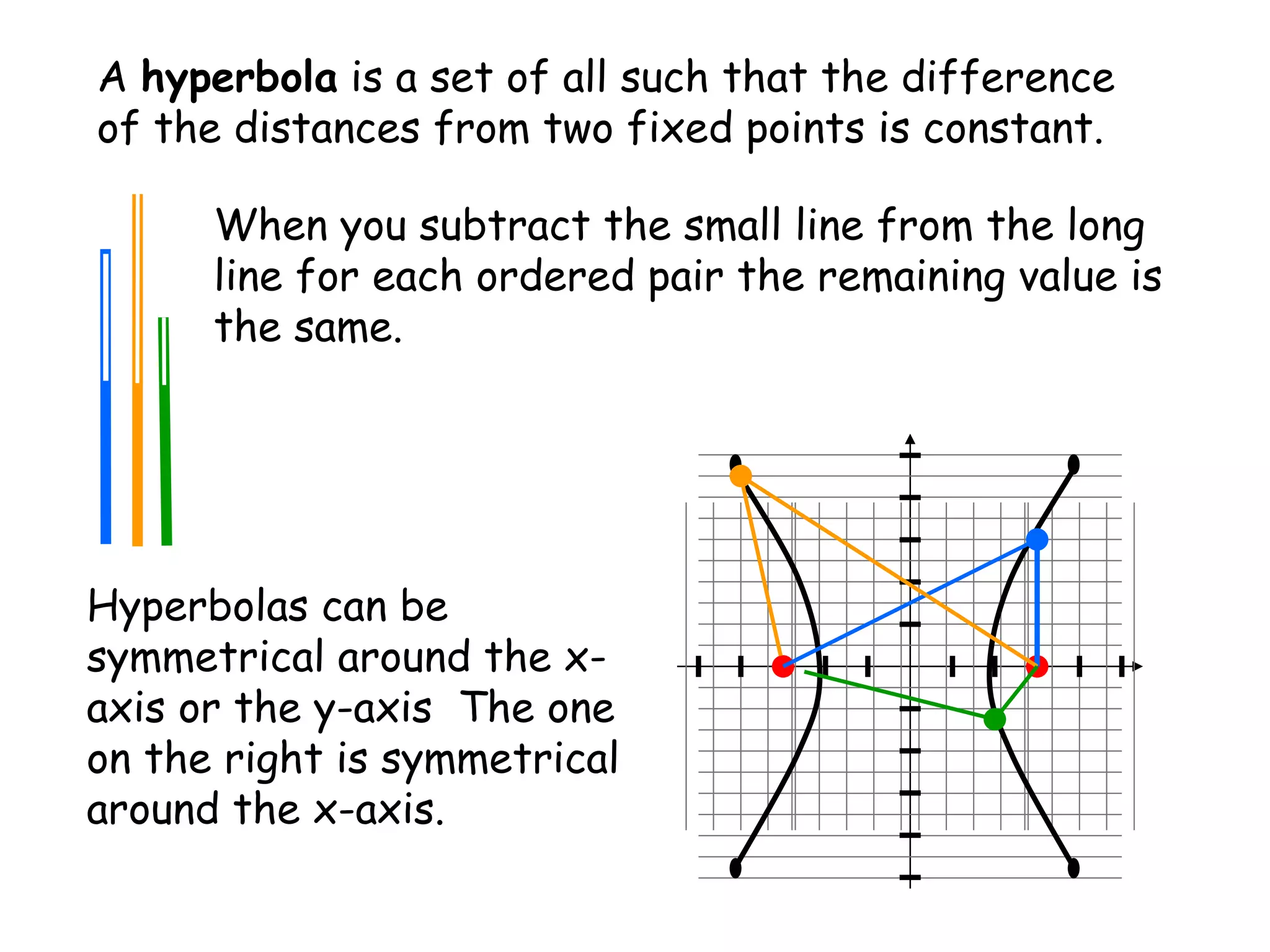
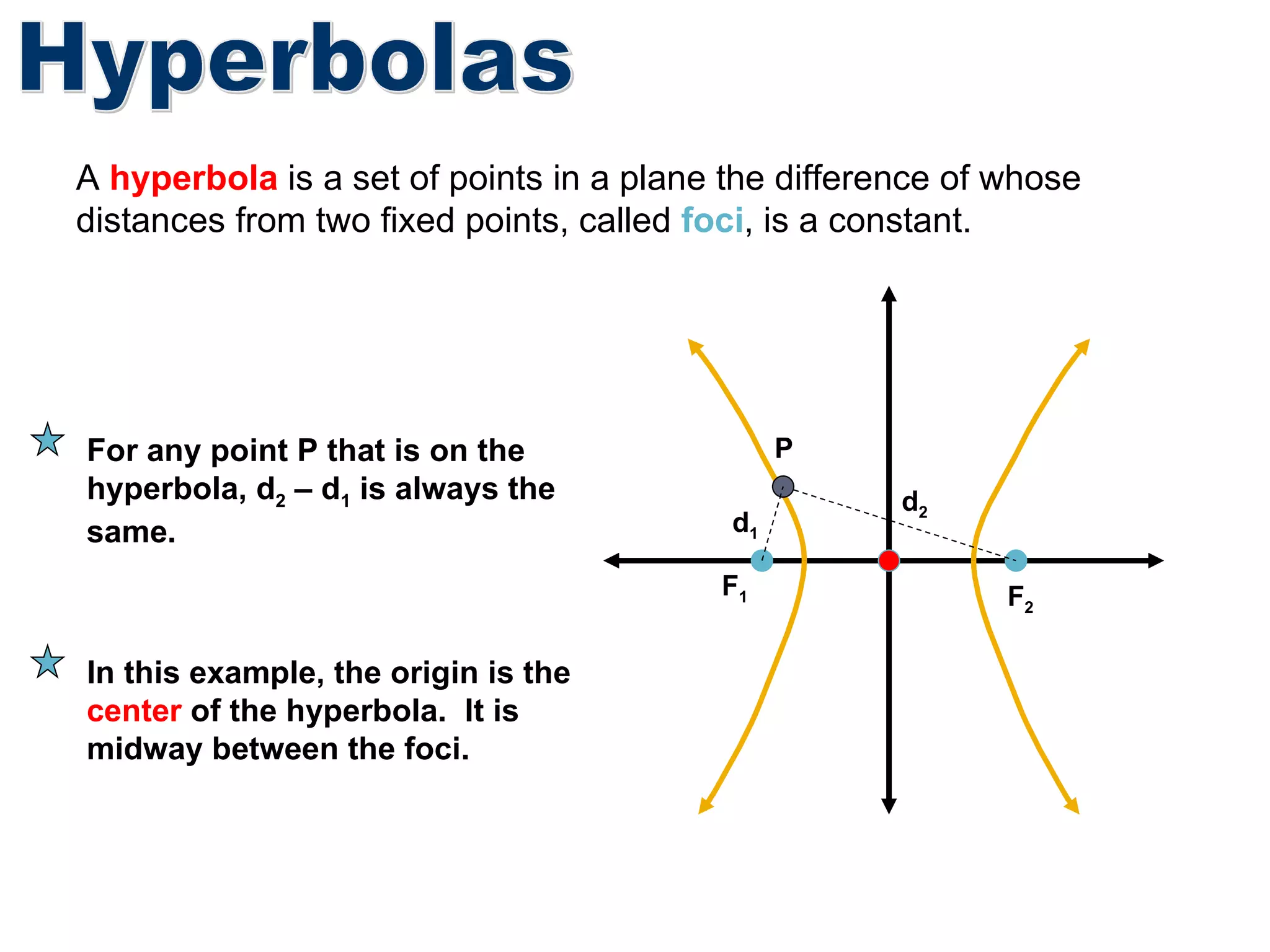
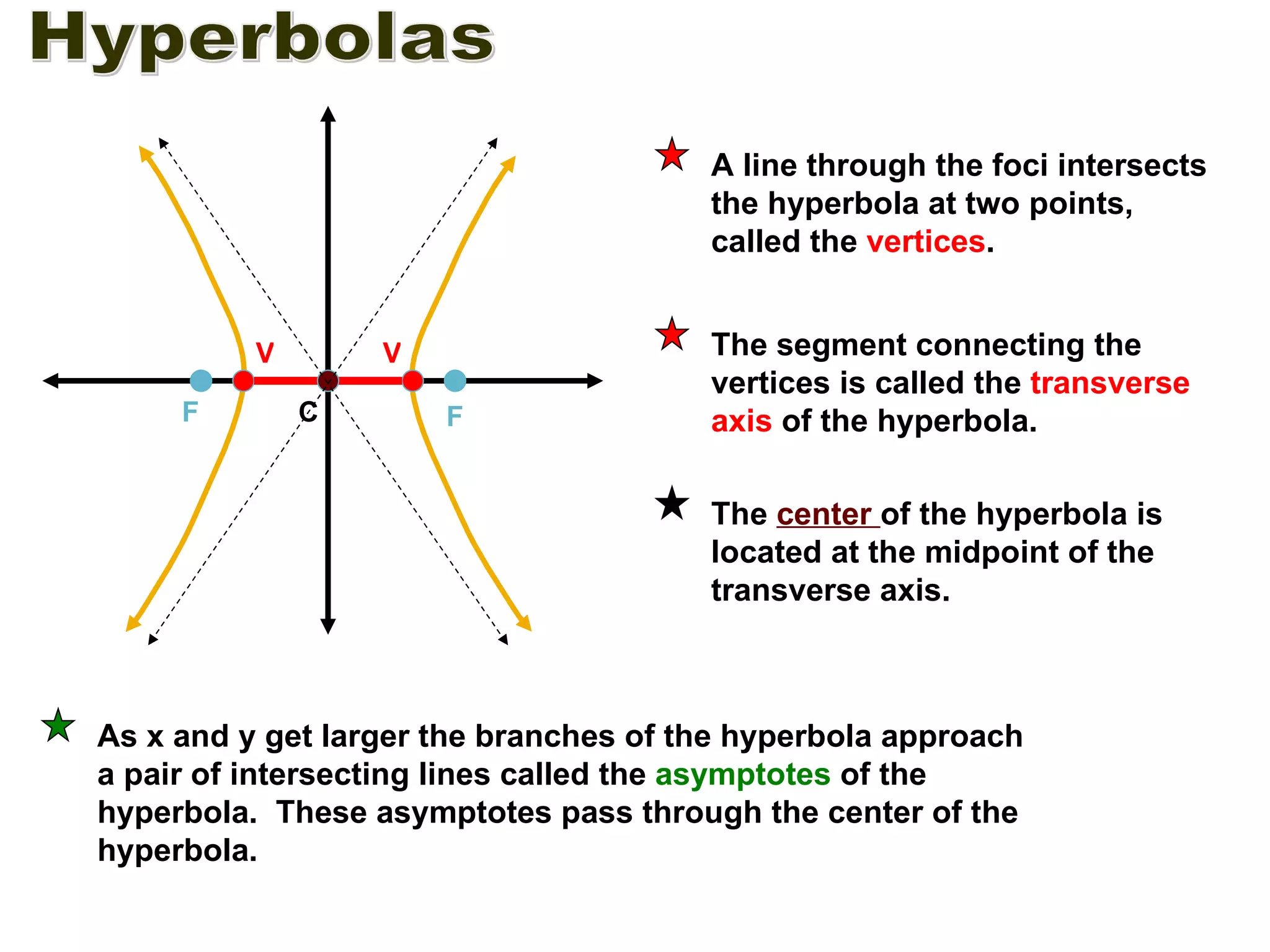
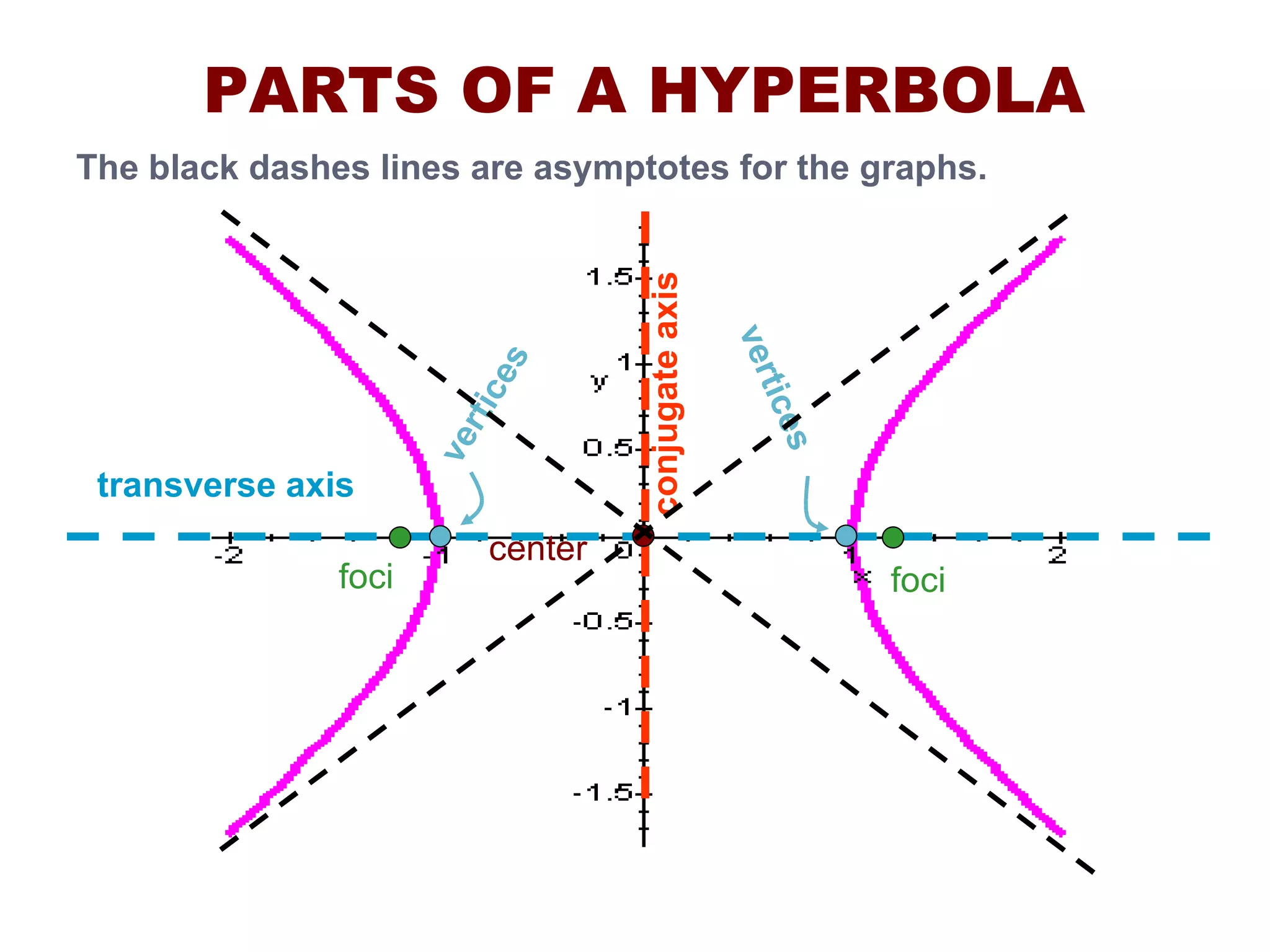
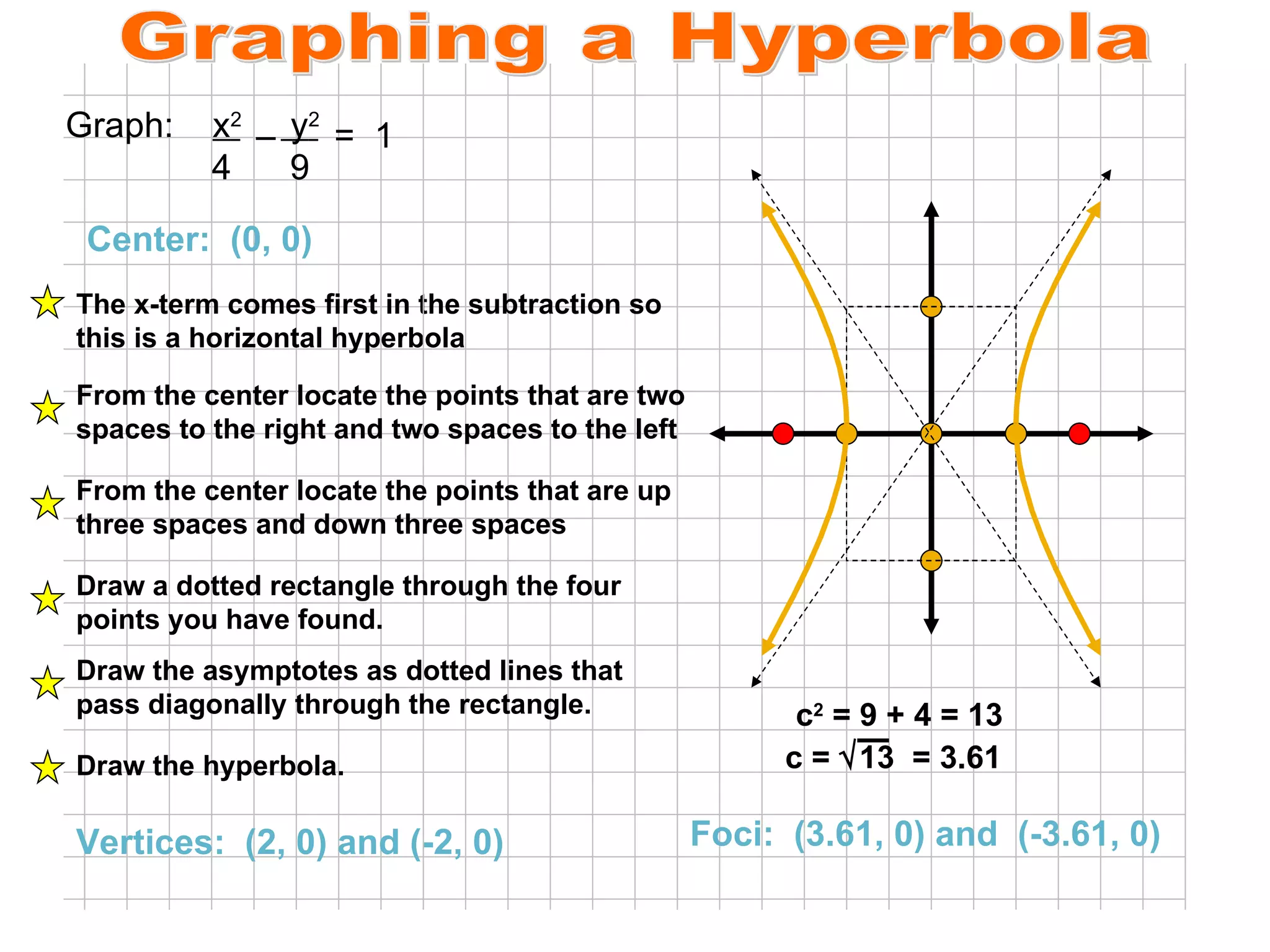
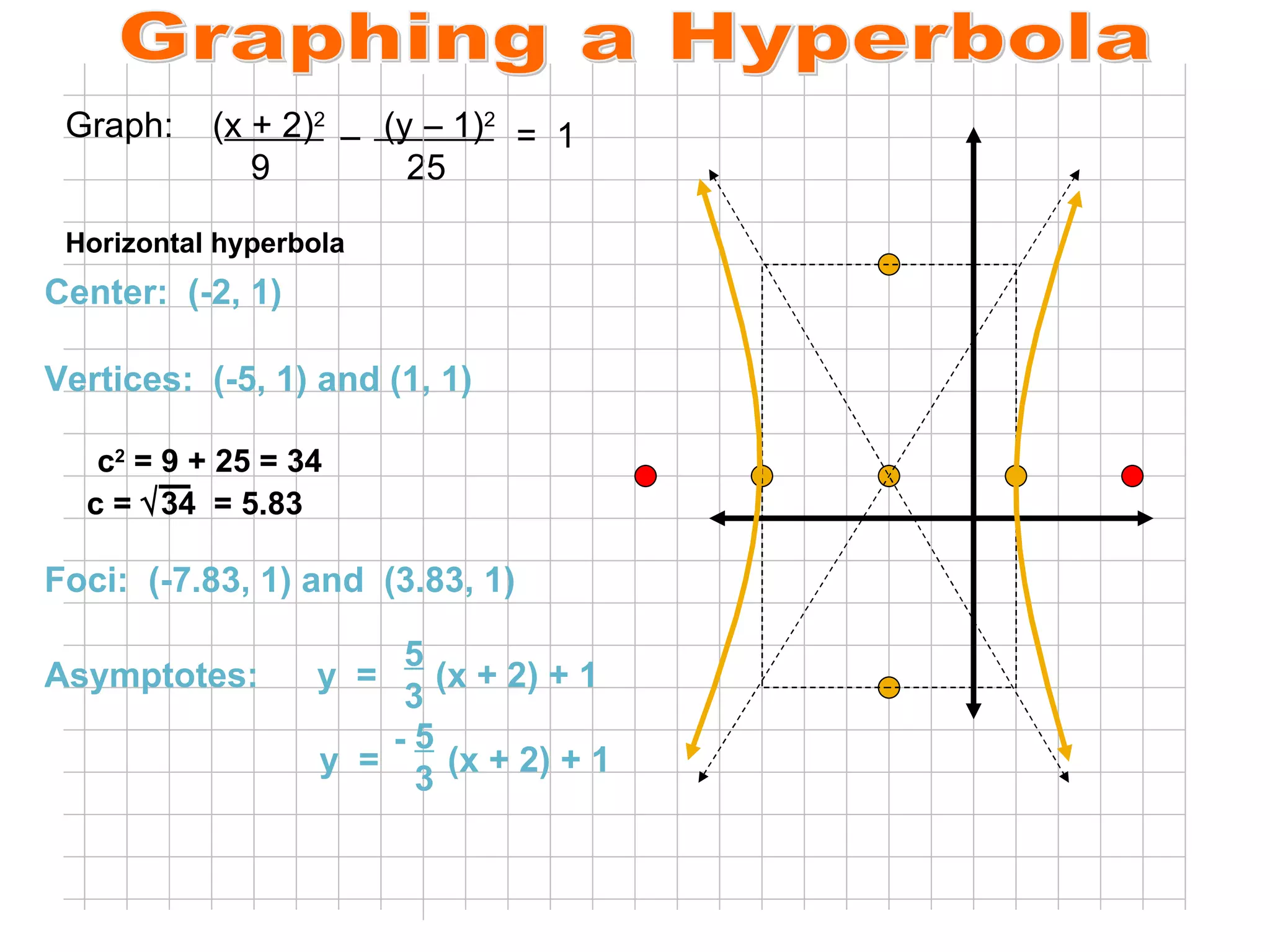
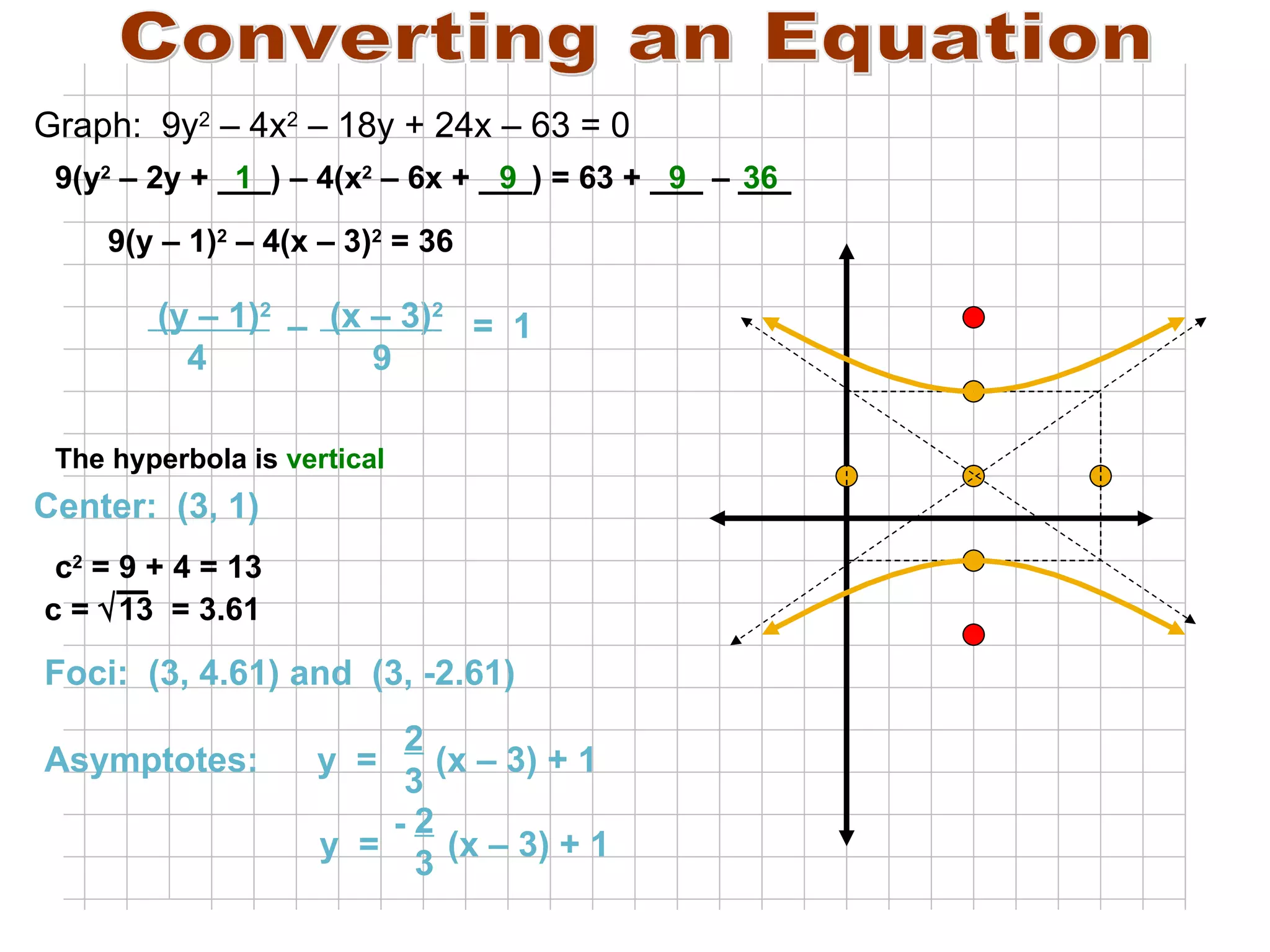
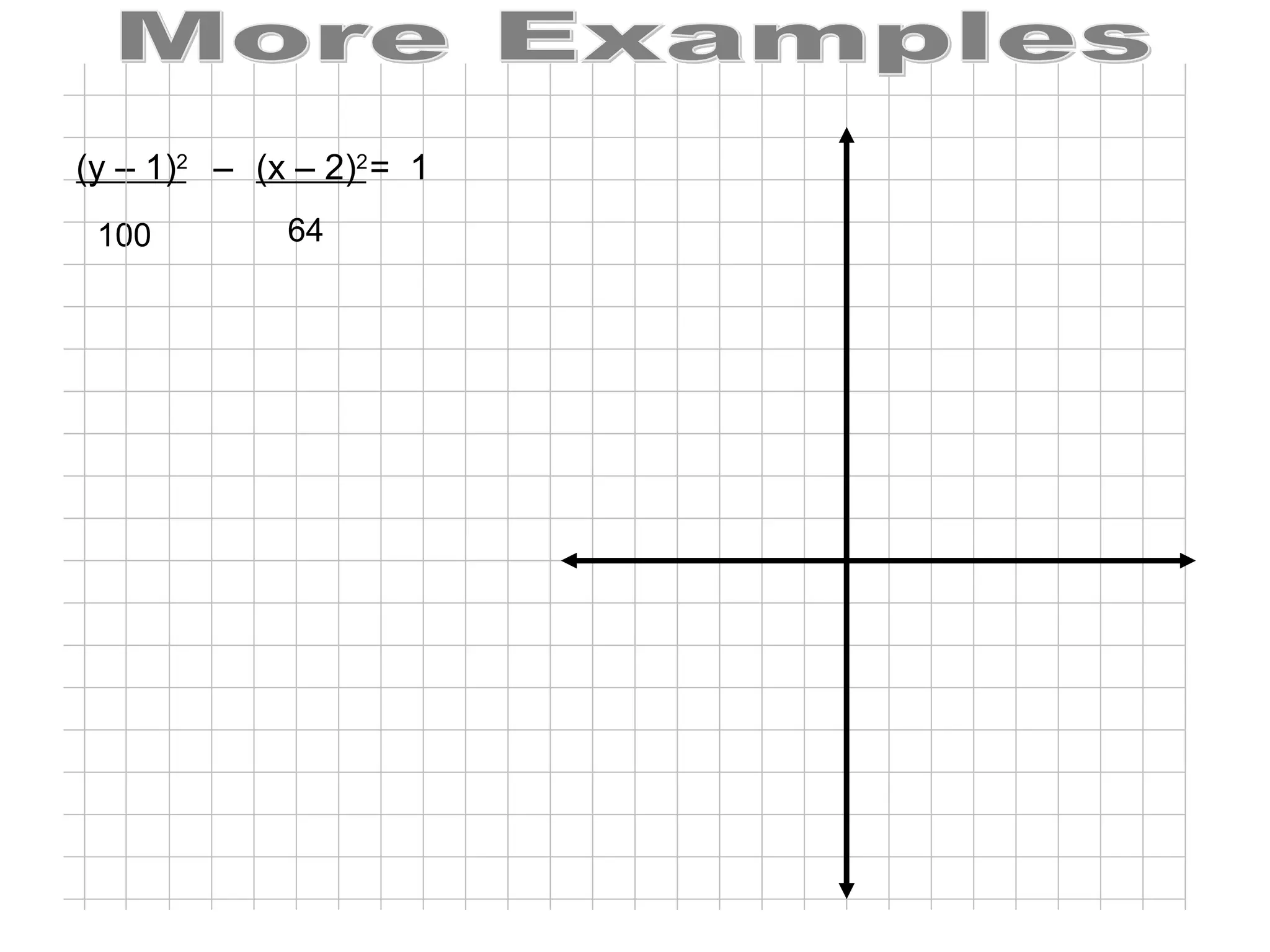
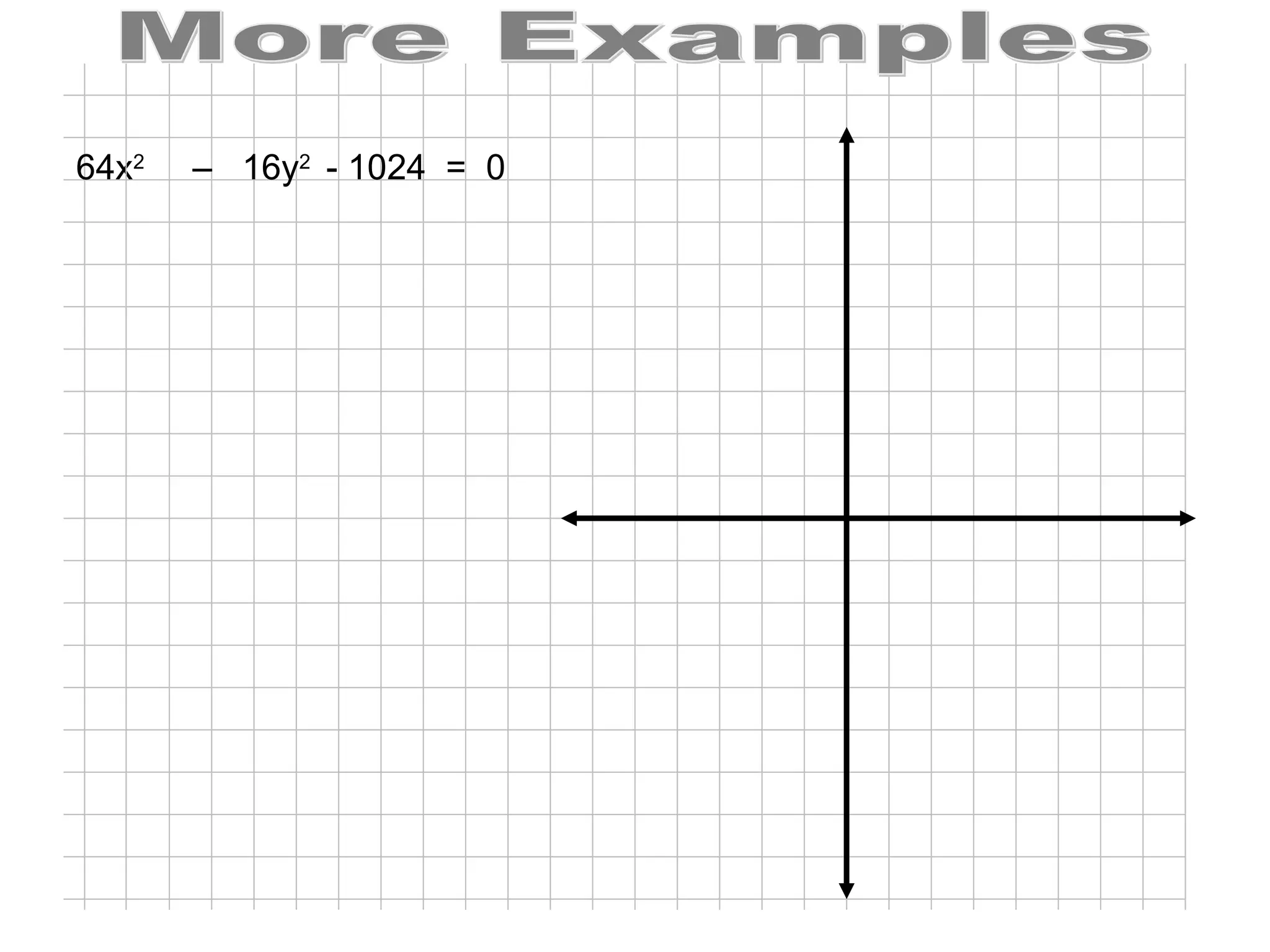
A hyperbola is the set of all points where the absolute difference between the distance to two fixed points (foci) is a constant. It is formed by the intersection of a plane with a double cone. The key parts of a hyperbola include the foci, vertices, center, and asymptotes. Hyperbolas can be written in standard form equations and graphed based on identifying these key parts.

1. A hyperbola is created from the intersection of a plane with a double cone.

2. A hyperbola is a set of all such that the difference of the distances from two fixed points is constant. When you subtract the small line from the long line for each ordered pair the remaining value is the same. Hyperbolas can be symmetrical around the x-axis or the y-axis The one on the right is symmetrical around the x-axis.

3. A hyperbola is a set of points in a plane the difference of whose distances from two fixed points, called foci , is a constant. Hyperbolas F 1 F 2 d 1 d 2 P For any point P that is on the hyperbola, d 2 – d 1 is always the same. In this example, the origin is the center of the hyperbola. It is midway between the foci.

4. Hyperbolas F F V V C A line through the foci intersects the hyperbola at two points, called the vertices . The segment connecting the vertices is called the transverse axis of the hyperbola. The center of the hyperbola is located at the midpoint of the transverse axis. As x and y get larger the branches of the hyperbola approach a pair of intersecting lines called the asymptotes of the hyperbola. These asymptotes pass through the center of the hyperbola.

5. Hyperbolas F F V V C The figure at the left is an example of a hyperbola whose branches open up and down instead of right and left. Since the transverse axis is vertical, this type of hyperbola is often referred to as a vertical hyperbola . When the transverse axis is horizontal, the hyperbola is referred to as a horizontal hyperbola .

6. PARTS OF A HYPERBOLA center foci foci conjugate axis vertices vertices The black dashes lines are asymptotes for the graphs. transverse axis

8. Standard Form Equation of a Hyperbola (x – h) 2 (y – k) 2 a 2 b 2 Horizontal Hyperbola (y – k) 2 (x – h) 2 b 2 a 2 – = 1 Vertical Hyperbola – = 1 The center of a hyperbola is at the point (h, k) in either form For either hyperbola, c 2 = a 2 + b 2 Where c is the distance from the center to a focus point. The equations of the asymptotes are y = (x – h) + k and y = (x – h) + k b a b a -

9. Graphing a Hyperbola Graph: x 2 y 2 4 9 c 2 = 9 + 4 = 13 c =  13 = 3.61 Foci: (3.61, 0) and (-3.61, 0) – = 1 Center: (0, 0) The x-term comes first in the subtraction so this is a horizontal hyperbola Vertices: (2, 0) and (-2, 0) From the center locate the points that are up three spaces and down three spaces Draw a dotted rectangle through the four points you have found. Draw the asymptotes as dotted lines that pass diagonally through the rectangle. Draw the hyperbola. From the center locate the points that are two spaces to the right and two spaces to the left

10. Graphing a Hyperbola Graph: ( x + 2) 2 (y – 1) 2 9 25 c 2 = 9 + 25 = 34 c =  34 = 5.83 Foci: (-7.83, 1) and (3.83, 1) – = 1 Center: (-2, 1) Horizontal hyperbola Vertices: (-5, 1) and (1, 1) Asymptotes: y = (x + 2) + 1 5 3 y = (x + 2) + 1 5 3 -

11. Converting an Equation (y – 1) 2 (x – 3) 2 4 9 c 2 = 9 + 4 = 13 c =  13 = 3.61 Foci: (3, 4.61) and (3, -2.61) – = 1 Center: (3, 1) The hyperbola is vertical Graph: 9y 2 – 4x 2 – 18y + 24x – 63 = 0 9(y 2 – 2y + ___) – 4(x 2 – 6x + ___) = 63 + ___ – ___ 9 1 9 36 9(y – 1) 2 – 4(x – 3) 2 = 36 Asymptotes: y = (x – 3) + 1 2 3 y = (x – 3) + 1 2 3 -

12. Center: (-1, -2) Vertical hyperbola Finding The Equation Find the standard form equation of the hyperbola that is graphed at the right (y – k) 2 (x – h) 2 b 2 a 2 – = 1 a = 5 and b = 3 (y + 2) 2 (x + 1) 2 25 9 – = 1

13. More Examples (y – 1) 2 (x – 2) 2 64 100 – = 1

14. More Examples 64x 2 16y 2 - 1024 – = 0

15. 1. 2. Find the center, foci , vertices and the equations of the asymptotes of the given hyperbolas, then graph.