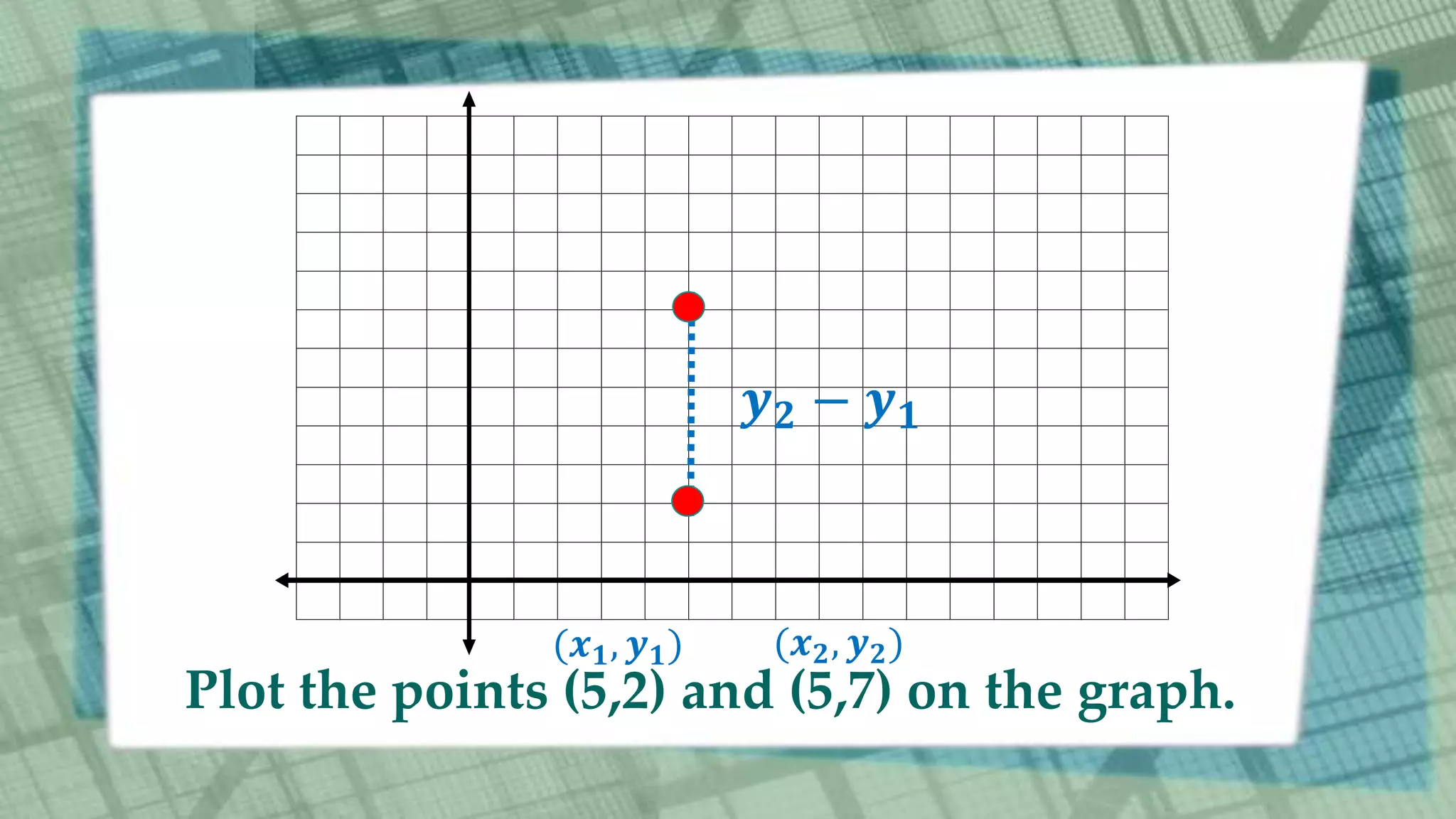
This document discusses coordinate geometry and the distance formula. It provides examples of using the distance formula to calculate the distance between points in the coordinate plane and to prove geometric properties, such as showing a triangle is isosceles or that four points form a square. It derives the distance formula and explains its components and how to apply it to find distances. Examples are provided to illustrate its use in solving geometry problems using algebraic methods in the coordinate plane.

3. COORDINATE
GEOMETRY
 Distance and Midpoint Formula
 Placing Figures in the Coordinate
Plane
 Coordinates in Proof
 Equation of a Circle

4. COORDINATE/ANALYTIC
GEOMETRY
-is the study of geometric figures
using algebra.

5. HOW USEFUL IS
COORDINATE
GEOMETRY?
“in what sense?”

12. DISTANCE
FORMULA
 Derive the distance formula
 Apply the distance formula to prove some geometric
properties

13. Plot the points (5,2) and (5,7) on the graph.
𝒚𝟐 − 𝒚𝟏
(𝒙𝟏, 𝒚𝟏) (𝒙𝟐, 𝒚𝟐)

14. Plot the points (-1,2) and (5,2) on the graph.
𝒙𝟐 − 𝒙𝟏

15. Connect the points (5,7) and (-1,2) on the graph.
𝒙𝟐 − 𝒙𝟏
𝒚𝟐 − 𝒚𝟏
𝒉𝒚𝒑𝒐𝒕𝒆𝒏𝒖𝒔𝒆

16. 𝑙𝑒𝑔 𝑜𝑛𝑒(𝑎) = 𝑥2 − 𝑥1
𝑙𝑒𝑔 𝑡𝑤𝑜 𝑏 = 𝑦2 − 𝑦1
ℎ𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 𝑐 = 𝑎2 + 𝑏2
ℎ𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒(𝑐) = 𝑑 = (𝑥2 − 𝑥1)2 + (𝑦2 − 𝑦1)2
===== Distance Formula

17. If A(𝑥1, 𝑦1) and B(𝑥2, 𝑦2) are
any two points on the
coordinate plan, then:
AB = (𝑥2 − 𝑥1)2+(𝑦2 − 𝑦1)2
THE DISTANCE FORMULA

18. Let: 𝒙𝟏 = 𝟎, 𝒙𝟐 = 𝟔, 𝒚𝟏 = 𝟎, 𝒚𝟐 = 𝟖
AB = (𝑥2 − 𝑥1)2+(𝑦2 − 𝑦1)2
= (6 − 0)2+(8 − 0)2
= 36 + 64
= 100
𝑨𝑩 = 𝟏𝟎
Use the Distance Formula to find the
distance between 𝑨(𝟎, 𝟎) and 𝑩(𝟔, 𝟖)
AB = (𝑥2 − 𝑥1)2+(𝑦2 − 𝑦1)2
= (6 − 0)2+(8 − 0)2
= 36 + 64
= 100
𝐀𝐁 = 𝟏𝟎 𝐮𝐧𝐢𝐭𝐬

19. The vertices of ∆𝑭𝑬𝑫 are 𝑭(𝟎, −𝟑), 𝑬(𝟑, 𝟑), and
𝑫(−𝟑, 𝟑). Show that ∆𝑭𝑬𝑫 is isosceles.

20. EF = (𝑥2 − 𝑥1)2+(𝑦2 − 𝑦1)2
= (0 − 3)2+(−3 − 3)2
= 9 + 81
= 90
𝑬𝑭 = 𝟑 𝟏𝟎
The vertices of ∆𝑭𝑬𝑫 are 𝑭(𝟎, −𝟑), 𝑬(𝟑, 𝟑), and
𝑫(−𝟑, 𝟑). Show that ∆𝑭𝑬𝑫 is isosceles.
DE = (𝑥2 − 𝑥1)2+(𝑦2 − 𝑦1)2
= (3 + 3)2+(3 − 3)2
= 62 + 02
= 36
𝐃𝐄 = 𝟔 𝐮𝐧𝐢𝐭𝐬

21. EF = (𝑥2 − 𝑥1)2+(𝑦2 − 𝑦1)2
= (0 − 3)2+(−3 − 3)2
= 9 + 81
= 90
𝑬𝑭 = 𝟑 𝟏𝟎
The vertices of ∆𝑭𝑬𝑫 are 𝑭(𝟎, −𝟑), 𝑬(𝟑, 𝟑), and
𝑫(−𝟑, 𝟑). Show that ∆𝑭𝑬𝑫 is isosceles.
EF = (𝑥2 − 𝑥1)2+(𝑦2 − 𝑦1)2
= (0 − 3)2+(−3 − 3)2
= (−3)2+(−6)2
= 45
𝐄𝐅 = 𝟑 𝟓 𝐮𝐧𝐢𝐭𝐬

22. EF = (𝑥2 − 𝑥1)2+(𝑦2 − 𝑦1)2
= (0 − 3)2+(−3 − 3)2
= 9 + 81
= 90
𝑬𝑭 = 𝟑 𝟏𝟎
The vertices of ∆𝑭𝑬𝑫 are 𝑭(𝟎, −𝟑), 𝑬(𝟑, 𝟑), and
𝑫(−𝟑, 𝟑). Show that ∆𝑭𝑬𝑫 is isosceles.
DF = (𝑥2 − 𝑥1)2+(𝑦2 − 𝑦1)2
= (0 + 3)2+(−3 − 3)2
= (3)2+(−6)2
= 45
𝐃𝐅 = 𝟑 𝟓 𝐮𝐧𝐢𝐭𝐬

23. Since
𝑬𝑭 = 𝑭𝑫 = 𝟑 𝟓
units, ∆𝑭𝑬𝑫 is an
isosceles triangle.
6
3 𝟓 3 𝟓

24. Prove that the points
A(-3,0), B(1,0), C(1,4),
and D(-3,4) are
vertices of a square.

25. Prove that the points A(-3,0), B(1,0), C(1,4),
and D(-3,4) are vertices of a square.
AB = (𝑥2 − 𝑥1)2+(𝑦2 − 𝑦1)2
= (1 + 3)2+(0 − 0)2
= (4)2+(0)2
= 16 + 0
= 16
𝐀𝐁 = 𝟒 𝐮𝐧𝐢𝐭𝐬

26. Prove that the points A(-3,0), B(1,0), C(1,4),
and D(-3,4) are vertices of a square.
BC = (𝑥2 − 𝑥1)2+(𝑦2 − 𝑦1)2
= (1 − 1)2+(4 − 0)2
= (0)2+(4)2
= 0 + 16
= 16
𝐁𝐂 = 𝟒 𝐮𝐧𝐢𝐭𝐬

27. Prove that the points A(-3,0), B(1,0), C(1,4),
and D(-3,4) are vertices of a square.
CD = (𝑥2 − 𝑥1)2+(𝑦2 − 𝑦1)2
= (−3 − 1)2+(4 − 4)2
= (−4)2+(0)2
= 16 + 0
= 16
𝐂𝐃 = 𝟒 𝐮𝐧𝐢𝐭𝐬

28. Prove that the points A(-3,0), B(1,0), C(1,4),
and D(-3,4) are vertices of a square.
AD = (𝑥2 − 𝑥1)2+(𝑦2 − 𝑦1)2
= (−3 + 3)2+(4 − 0)2
= (0)2+(4)2
= 0 + 16
= 16
𝐀𝐃 = 𝟒 𝐮𝐧𝐢𝐭𝐬

29. Prove that the points A(-3,0), B(1,0), C(1,4),
and D(-3,4) are vertices of a square.
Since
𝑨𝑩 = 𝑩𝑪 = 𝑪𝑫 = 𝑨𝑫 = 𝟒 units,
the given points are vertices of
a square.

30. If A(𝑥1, 𝑦1) and B(𝑥2, 𝑦2) are
any two points on the
coordinate plan, then:
AB = (𝑥2 − 𝑥1)2+(𝑦2 − 𝑦1)2
THE DISTANCE FORMULA

33. ASSIGNMENT
In a graphing paper, answer
numbers 11, 21, 26, and 32 on
pages 353-354. Be able to show
your complete process.