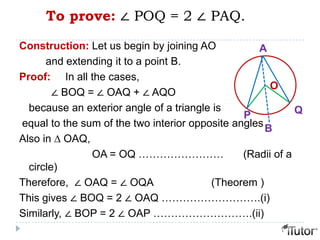
This document provides definitions and theorems related to circles. It defines circle terms like radius, diameter, chord, arc, tangent, and sector. It proves theorems such as a perpendicular from the center of a circle to a chord bisects the chord; equal chords subtend equal angles; and the angle subtended by an arc at the center is double the angle at any other point on the circle. It also proves properties of tangents, like tangents from an external point being equal lengths.

1. T- 1-855-694-8886
Email- info@iTutor.com
By iTutor.com

2. A Circle features…….
the distance around the Circle…
… its PERIMETER
Diameter
Radius … the distance across the
circle, passing through the centre
of the circle
Radius
Diameter...
the distance from the centre of
the circle to any point on the
circumference

3. A Circle features…….
Chord -> a line joining two points
on the Circumference.
… chord divides circle into
two segments
ARC -> part of the
circumference of a circle
Major
Segment
Minor
Segment
Tangent -> a line which touches
the circumference at one point
only

4. A perpendicular from the centre of a circle to
a chord bisects the chord.
Given: AB is a chord in a circle with centre O. OC ⊥ AB.
To prove: The point C bisects the chord AB.
Construction: Join OA and OB
Proof: In ∆ OAC and ∆ OBC,
∠OCA = ∠OCB = 90…………(Given)
OA = OB …………………..(Radii)
OC = OC ……………….(common side)
∠OAC = ∠OBC ………………………..(RHS)
CA = CB (corresponding sides)
The point C bisects the chord AB.
Hence the theorem is proved.
0
A B
O
C

5. The line drawn through the centre of a circle to bisect
a chord is perpendicular to the chord.
Given: AB be a chord of a circle with centre O and O is joined to the mid-
point M of AB.
To prove: OM ⊥ AB
Construction:
Join OA and OB.
Proof:
In ∆ OAM & ∆ OBM,
OA = OB……………. (Radii of a circle)
AM = BM ……………..(Given)
OM = OM (Common)
Therefore, ∆OAM ≅ ∆OBM ……………………….(SSS Rule)
This gives ∠OMA = ∠OMB = 90°
0
A B
O
M

6. Equal chords of a circle subtend equal
angles at the centre.
Given: Two equal chords AB and CD of a circle with centre O
To Prove: ∠ AOB = ∠ COD
In ∆ AOB and ∆ COD,
OA = OC……. (Radii of a circle)
OB = OD………..(Radii of a circle)
AB = CD ………...(Given)
Therefore,
∆ AOB ≅ ∆ COD…………. (SSS rule)
This gives ∠ AOB = ∠ COD
(Corresponding parts of congruent triangles)
OA
B
C
D

7. The angle subtended by an arc at the centre is double the
angle subtended by it at any point on the remaining part of
the circle.
Given: An arc PQ of a circle subtending angles POQ at the
centre O and PAQ at a point A on the remaining part of the
circle.
To prove: ∠ POQ = 2 ∠ PAQ.
P
Q
O
O O
P
Q
A
Q
AA
P
(i) arc PQ is minor (ii)arc PQ is a semicircle iii)arc PQ is major.

8. Construction: Let us begin by joining AO
and extending it to a point B.
Proof: In all the cases,
∠ BOQ = ∠ OAQ + ∠ AQO
because an exterior angle of a triangle is
equal to the sum of the two interior opposite angles
Also in ∆ OAQ,
OA = OQ …………………… (Radii of a
circle)
Therefore, ∠ OAQ = ∠ OQA (Theorem )
This gives ∠ BOQ = 2 ∠ OAQ ……………………….(i)
Similarly, ∠ BOP = 2 ∠ OAP ……………………….(ii)
A
P Q
O
B
To prove: ∠ POQ = 2 ∠ PAQ.

9. From (i) and (ii) we get,
∠ BOP + ∠ BOQ = 2 (∠ OAP + ∠ OAQ)
Now,
∠ POQ = 2 ∠ PAQ …………………..(iii)
For the case (iii)where PQ is the major arc
(iii) is replaced by reflex angle
POQ = 2 ∠ PAQ
Proved
A
P Q
O
B
To prove: ∠ POQ = 2 ∠ PAQ.
O
Q
A
P
B

10. Opposite Angles in a Cyclic Quadrilateral
are supplementary
Required to Prove that x + y = 180º
x
2x
y
2y
Draw in radii
The angle at the centre is
TWICE the angle at the
circumference
2x + 2y = 360º
2(x + y) = 360º
x + y = 180º
Opposite Angles in Cyclic Quadrilateral are Supplementary

11. Tangent to a Circle
The tangent at any point of a circle is perpendicular to the
radius through the point of contact
Given: a circle with centre O and a tangent XY to the circle
at a point P.
To prove: OP is perpendicular to XY.
Construction: Take a point Q on XY
other than P and join OQ ,
The point Q must lie outside the circle.
Proof: OQ is longer than the radius
OP of the circle. That is,
OQ > OP
O
X YP Q

12. Tangent to a Circle
Since this happens for every point on the
line XY except the point P, OP is the
shortest of all the distances of the point O to the
points of XY.
So OP is perpendicular to XY
O
X YP Q

13. Tangent to a Circle
 The lengths of tangents drawn from an external point to a
circle are equal.
Given: A circle with centre O, a point P
lying outside the circle and two tangents
PQ, PR on the circle from P
To prove: PQ = PR.
Construction: With centre of circle at O,
draw straight lines OA and OB, Draw straight line OP.
O
Q
R
P

14. O
Q
R
P
Tangent to a Circle
Proof: In right triangles OQP and ORP,
OQ = OR .......................(radii of the same circle)
∠ OQP = ∠ ORP ………………..(right angles)
OP = OP ………………(Common)
Therefore,
Δ OQP ≅ Δ ORP ……..(RHS)
This gives
PQ = PR …………..(CPCT)

15. The End
Call us for more
information:
www.iTutor.com
1-855-694-8886
Visit