長岡技術科学大学
2015年度先端GPGPUシミュレーション工学特論(全15回,大学院生対象講義)
第10回Poisson方程式の求解�(線形連立一次方程式)
2015年度先端GPGPUシミュレーション工学特論
・第1回 先端シミュレーションおよび産業界におけるGPUの役割
http://www.slideshare.net/ssuserf87701/2015gpgpu1-59180313
・第1回補足 GROUSEの利用方法
http://www.slideshare.net/ssuserf87701/2015gpgpu1-59180326
・第2回 GPUによる並列計算の概念とメモリアクセス
http://www.slideshare.net/ssuserf87701/2015gpgpu2-59180382
・第3回 GPUプログラム構造の詳細(threadとwarp)
http://www.slideshare.net/ssuserf87701/2015gpgpu3-59180483
・第4回 GPUのメモリ階層の詳細(共有メモリ)
http://www.slideshare.net/ssuserf87701/2015gpgpu4-59180572
・第5回 GPUのメモリ階層の詳細(様々なメモリの利用)
http://www.slideshare.net/ssuserf87701/2015gpgpu5-59180652
・第6回 プログラムの性能評価指針(Flop/Byte,計算律速,メモリ律速)
http://www.slideshare.net/ssuserf87701/2015gpgpu6-59180736
・第7回 総和計算(Atomic演算)
http://www.slideshare.net/ssuserf87701/2015gpgpu7-59180844
・第8回 偏微分方程式の差分計算(拡散方程式)
http://www.slideshare.net/ssuserf87701/2015gpgpu8-59180918
・第9回 偏微分方程式の差分計算(移流方程式)
http://www.slideshare.net/ssuserf87701/2015gpgpu9-59180982
・第10回 Poisson方程式の求解(線形連立一次方程式)
http://www.slideshare.net/ssuserf87701/2015gpgpu10-59181031
・第11回 数値流体力学への応用(支配方程式,CPUプログラム)
http://www.slideshare.net/ssuserf87701/2015gpgpu11-59181134
・第12回 数値流体力学への応用(GPUへの移植)
http://www.slideshare.net/ssuserf87701/2015gpgpu12-59181230
・第13回 数値流体力学への応用(高度な最適化)
http://www.slideshare.net/ssuserf87701/2015gpgpu13-59181316
・第14回 複数GPUの利用
http://www.slideshare.net/ssuserf87701/2015gpgpu14-59181367
・第15回 CPUとGPUの協調
http://www.slideshare.net/ssuserf87701/2015gpgpu15-59181450
2015年度GPGPU実践基礎工学
・第1回 学際的分野における先端シミュレーション技術の歴史
http://www.slideshare.net/ssuserf87701/2015gpgpu1
2015年度GPGPU実践プログラミング
・第1回 GPGPUの歴史と応用例
http://www.slideshare.net/ssuserf87701/2015gpgpu1-59179080
講義には長岡技術科学大学のGPGPUシステム(GROUSE)を利用しています。
開発環境
CPU Intel Xeon X5670 × 32
GPU NVIDIA Tesla M2050(Fermi世代) × 64
CUDA 4.0(諸般の事情によりバージョンアップされていません)
PGI Fortran 11.3






















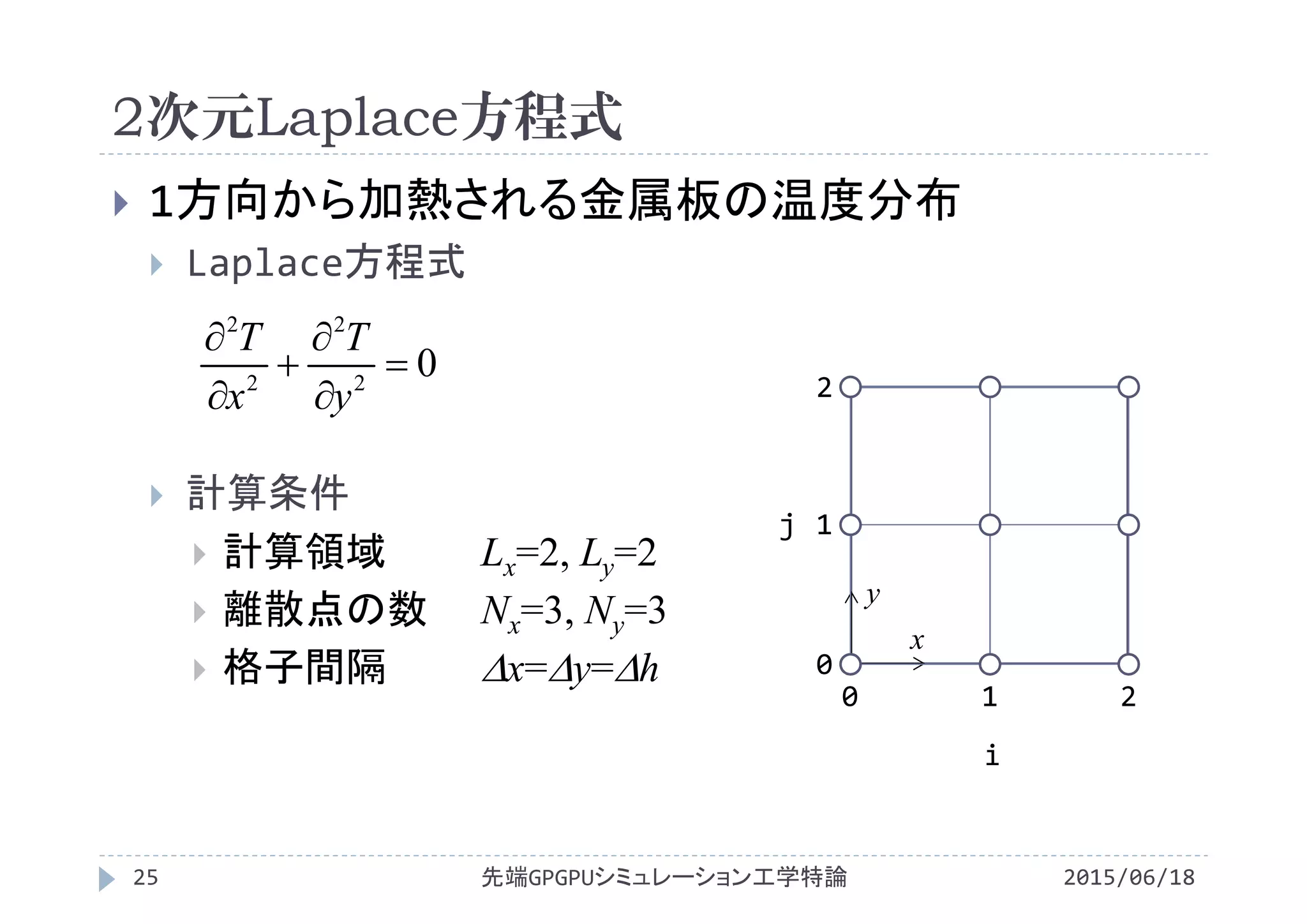
![2次元Laplace方程式
2015/06/18先端GPGPUシミュレーション工学特論26
1方向から加熱される金属板の温度分布
Laplace方程式
Laplace方程式の差分式
02
2
2
2
y
T
x
T
0
i
1 2
0
1
2
j
T[i][j]
0
22
2
1,,1,
2
,1,,1
y
TTT
x
TTT jijijijijiji
0
4
2
1,,1,1,,1
h
TTTTT jijijijiji](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-26-2048.jpg)
![2次元Laplace方程式
2015/06/18先端GPGPUシミュレーション工学特論27
1方向から加熱される金属板の温度分布
Laplace方程式
Laplace方程式の差分式
0
i
1 2
0
1
2
j
T[]
0 1 2
3 4 5
6 7 8
0
22
2
147
2
345
y
TTT
x
TTT
0
4
2
13475
h
TTTTT
02
2
2
2
y
T
x
T](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-27-2048.jpg)
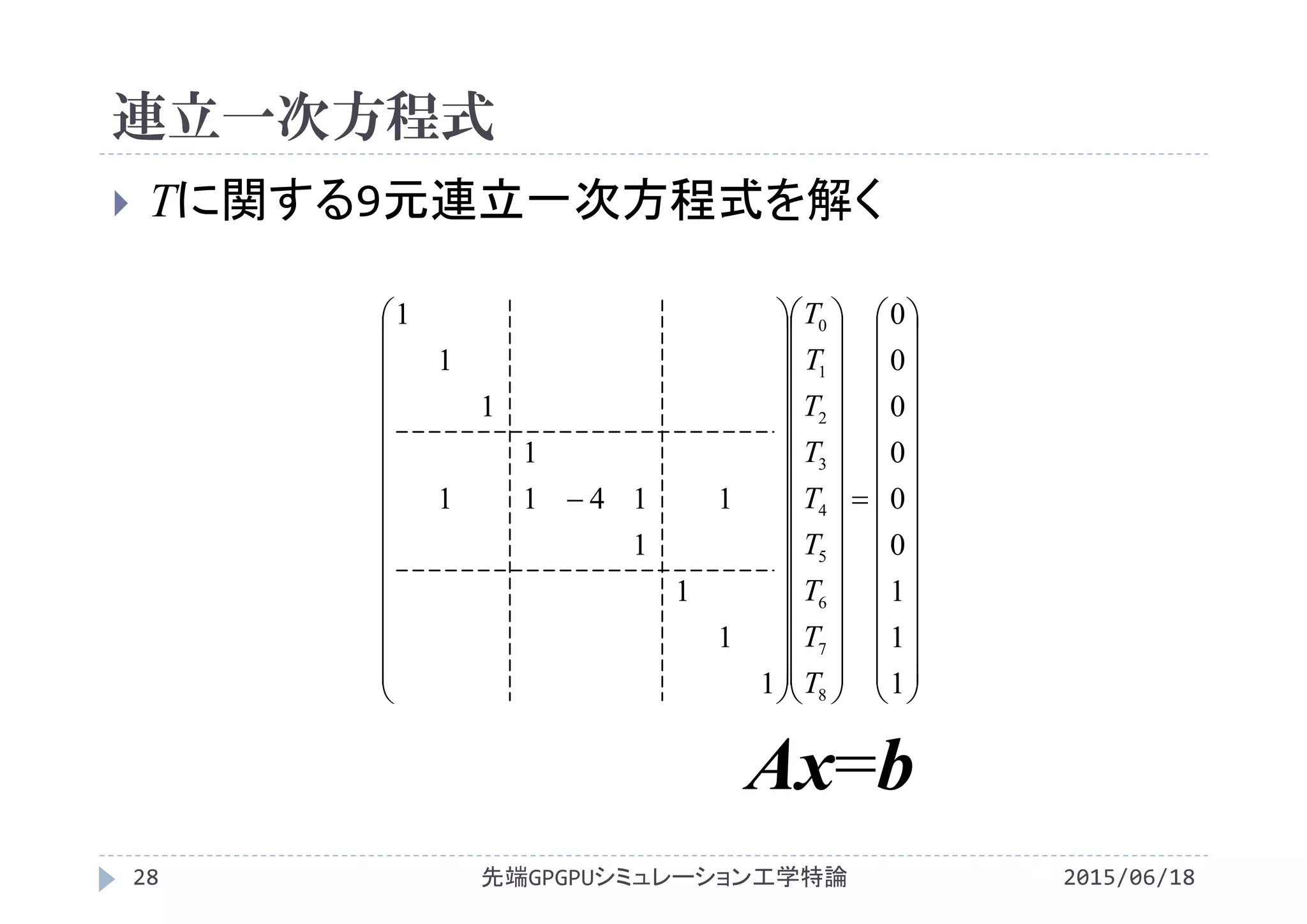
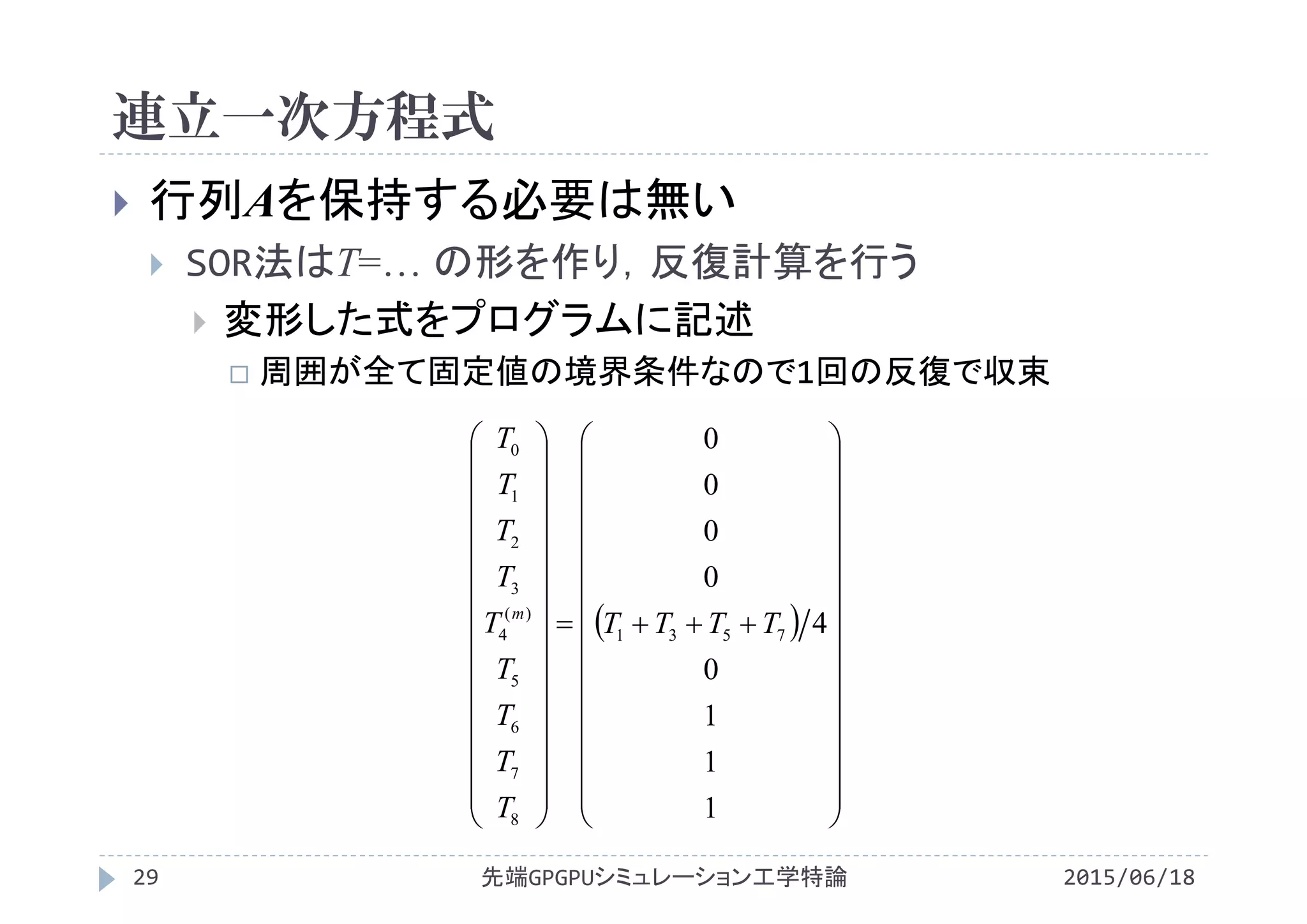
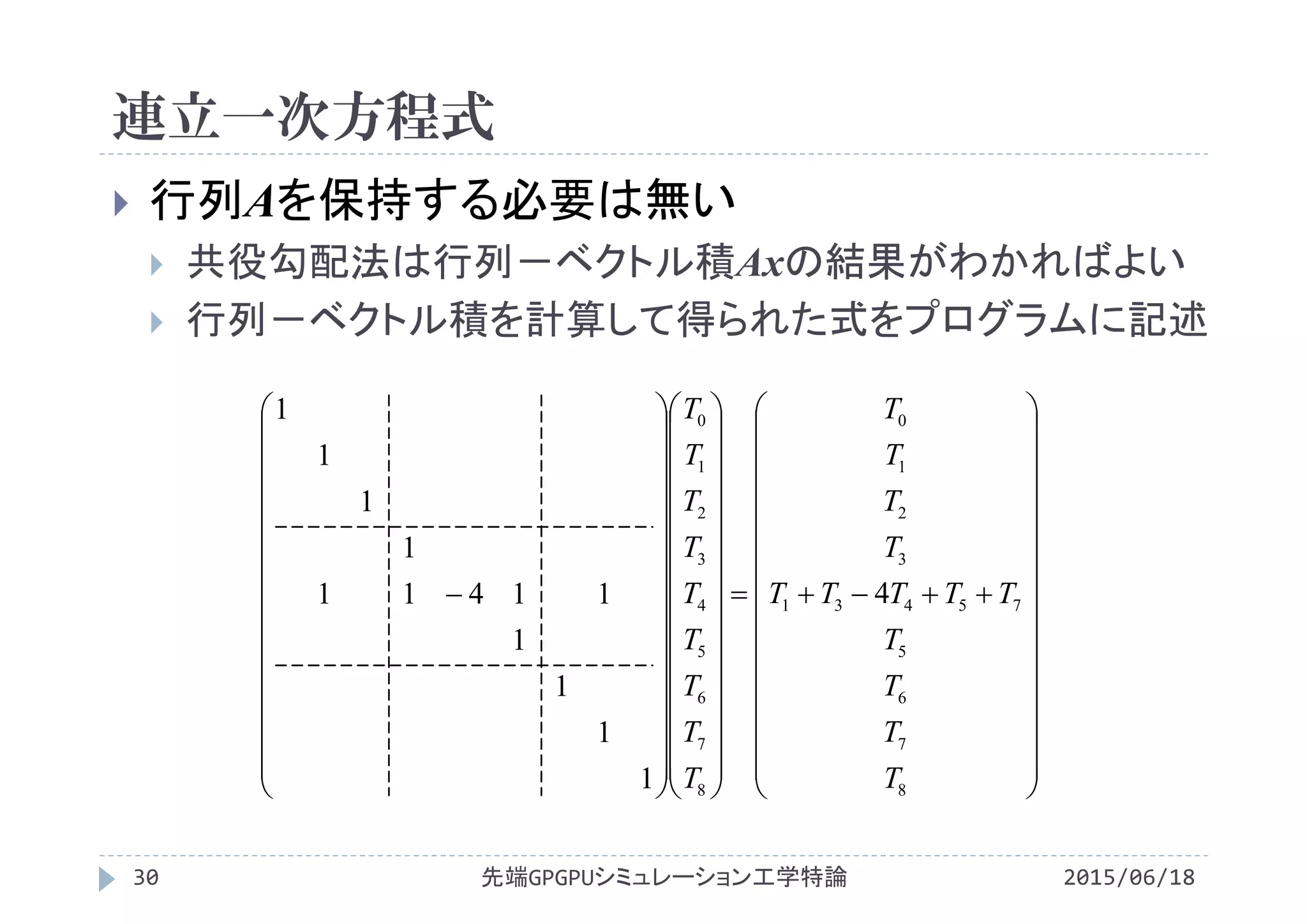
![#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#define Lx 2.0
#define Ly Lx
#define Nx 11
#define Ny Ny
#define dx (Lx/(Nx‐1))
#define dy dx
#define dxdx (dx*dx)
#define dydy (dy*dy)
#define Nbytes (Nx*Ny*sizeof(double))
#define ERR_TOL 1e‐12
#define Accel 1.0
void sor(double *T);
void cg(double *T);
void init(double *T){
for(int j=0;j<Ny;j++){
for(int i=0;i<Nx;i++){
T[i+Nx*j] = 0.0;
}
}
}
int main(void){
double *T;
T = (double *)malloc(Nbytes);
init(T);
sor(T)
//cg(T);
return 0;
}
CPUプログラム(メイン・初期化)
2015/06/18先端GPGPUシミュレーション工学特論31
laplace.c](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-31-2048.jpg)
![void sor(double *T){
int ite_SOR=0;
double err_n,err_d,err_relative;
double d_t;
int ij,ip1j,im1j,ijm1,ijp1;
//境界条件の適用
for(int i=0;i<Nx;i++){
ij = i+Nx*(Ny‐1); //j=Ny‐1
T[i+Nx*j] = 1.0;
}
do{
err_n = 0.0;
err_d = 0.0;
for(int j=1;j<Ny‐1;j++){
for(int i=1;i<Nx‐1;i++){
ij = i+Nx*j;
ip1j = (i+1)+Nx*(j );
im1j = (i‐1)+Nx*(j );
ijp1 = (i )+Nx*(j+1);
ijm1 = (i )+Nx*(j‐1);
d_t =( (T[im1j]+T[ip1j])
+(T[ijm1]+T[ijp1])
)/(‐4.0) ‐T[ij];
T[ij] += Accel*d_t;
err_n += d_t*d_t;
err_d += T[ij]*T[ij];
}
}
if(err_d<1e‐20)err_d=1.0;
err_relative = sqrt(err_n/err_d);
ite_SOR++;
}while(err_relative > ERR_TOL);
}
CPUプログラム(SOR法)
2015/06/18先端GPGPUシミュレーション工学特論32
laplace.c](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-32-2048.jpg)
![void cg(double *T){
double err;
int ij,ip1j,im1j,ijm1,ijp1;
double *p,*r,*Ap;
double alph,beta,rr,pAp;
//境界条件の適用
for(int i=0;i<Nx;i++){
ij=i+Nx*(Ny‐1);//j=Ny‐1
T[i+Nx*j] = 1.0;
}
p = (double *)malloc(Nbytes);
r = (double *)malloc(Nbytes);
Ap = (double *)malloc(Nbytes);
for(int j=0;j<Ny;j++){
for(int i=0;i<Nx;i++){
ij = i+Nx*j;
p [ij] = 0.0;
r [ij] = 0.0;
Ap[ij] = 0.0;
}
}
alph=0.0;
beta=0.0;
rr = 0.0;
for(int j=1;j<Ny‐1;j++){
for(int i=1;i<Nx‐1;i++){
ij = i+Nx*j;
ip1j = (i+1)+Nx*(j );
im1j = (i‐1)+Nx*(j );
ijp1 = (i )+Nx*(j+1);
ijm1 = (i )+Nx*(j‐1);
r[ij] = ‐( (T[im1j]‐2*T[ij]+T[ip1j])/dxdx
+(T[ijm1]‐2*T[ij]+T[ijp1])/dydy);
rr += r[ij]*r[ij];
}
}
CPUプログラム(共役勾配法)
2015/06/18先端GPGPUシミュレーション工学特論33
laplace.c](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-33-2048.jpg)
![do{
for(int j=0;j<Ny;j++){
for(int i=0;i<Nx;i++){
ij = i+Nx*j;
p [ij] = r[ij] + beta*p[ij];
}
}
pAp = 0.0;
for(int j=1;j<Ny‐1;j++){
for(int i=1;i<Nx‐1;i++){
ij = i+Nx*j;
ip1j = (i+1)+Nx*(j );
im1j = (i‐1)+Nx*(j );
ijp1 = (i )+Nx*(j+1);
ijm1 = (i )+Nx*(j‐1);
Ap[ij] = (p[im1j]‐2*p[ij]+p[ip1j])/dxdx
+(p[ijm1]‐2*p[ij]+p[ijp1])/dydy;
pAp += p[ij]*Ap[ij];
}
}
alph = rr/pAp;
rr = 0.0;
for(int j=0;j<Ny;j++){
for(int i=0;i<Nx;i++){
ij = i+Nx*j;
T[ij] = T[ij] + alph* p[ij];
r[ij] = r[ij] ‐ alph*Ap[ij];
rr += r[ij]*r[ij];
}
}
err = sqrt(rr);
beta = rr/(alph*pAp);
}while(err > ERR_TOL);
}
CPUプログラム(共役勾配法)
2015/06/18先端GPGPUシミュレーション工学特論34
laplace.c](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-34-2048.jpg)

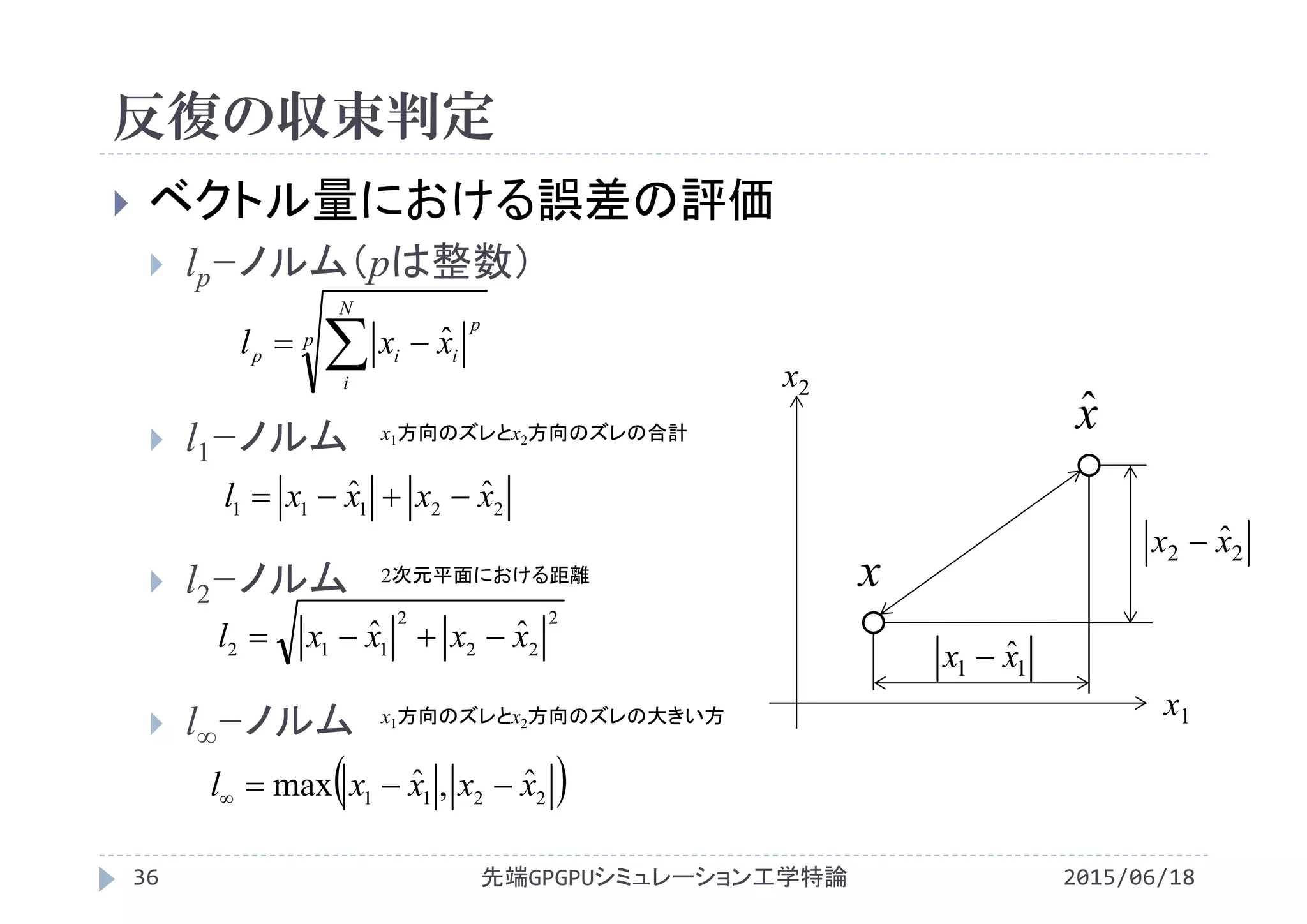
![反復の収束判定
2015/06/18先端GPGPUシミュレーション工学特論37
l2−ノルムを用いた相対
誤差評価
m+1回目の反復の値が
真値になれば誤差と一致
反復中に変化量が十分
小さくなれば収束と判定
x2
y x
y x
N
j
N
i
m
ji
N
j
N
i
m
ji
m
ji
T
TT
2)1(
,
2)(
,
)1(
,
err_n = 0.0;
err_d = 0.0;
for(int j=1;j<Ny‐1;j++){
for(int i=1;i<Nx‐1;i++){
d_t =( (T[im1j]+T[ip1j])
+(T[ijm1]+T[ijp1])
)/(‐4.0) ‐T[ij];
T[ij] += Accel*d_t;
err_n += d_t*d_t;
err_d += T[ij]*T[ij];
}
}
if(err_d<1e‐20)err_d=1.0;
err_relative = sqrt(err_n/err_d);](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-37-2048.jpg)

![反復の収束判定
2015/06/18先端GPGPUシミュレーション工学特論39
残差の2乗ノルムを用
いた収束判定
右辺の2乗ノルムを用い
た相対残差を計算 x2
y x
y x
N
j
N
i
ji
N
j
N
i
m
ji
b
r
2
,
2)1(
,
rr = 0.0;
for(int j=1;j<Ny‐1;j++){
for(int i=1;i<Nx‐1;i++){
ij = i+Nx*j;
ip1j = (i+1)+Nx*(j );
im1j = (i‐1)+Nx*(j );
ijp1 = (i )+Nx*(j+1);
ijm1 = (i )+Nx*(j‐1);
r[ij] = ‐( (T[im1j]‐2*T[ij]+T[ip1j])/dxdx
+(T[ijm1]‐2*T[ij]+T[ijp1])/dydy);
rr += r[ij]*r[ij];
}
}
・・・
//右辺が0でなければ右辺のl2ノルムbbで
//割った値の平方根sqrt(rr/bb)を評価
err = sqrt(rr);](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-39-2048.jpg)
![計算結果
2015/06/18先端GPGPUシミュレーション工学特論40
前回授業で用いたgnuplotのanim_2d.gplを流用
して2次元分布を確認
set xrange [0:2] x軸の表示範囲を0~2に固定
set yrange [0:2] y軸の表示範囲を0~2に固定
set zrange [0:1] z軸の表示範囲を0~1に固定
set view 0,0 真上から見下ろす
set size 1,1 グラフの縦横比を1:1
set contour 2次元等高線を表示
unset surface 3次元で等値面を表示しない
unset pm3d カラー表示しない
set cntrparam levels incremental 0,0.1,1
等高線を0から1まで0.1刻みに設定
以下でファイルを読み込み,3次元表示
splot 'T.txt' with line](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-40-2048.jpg)
![計算結果
2015/06/18先端GPGPUシミュレーション工学特論41
前回授業で用いたgnuplotのanim_2d.gplを流用
して2次元分布を確認
set xrange [0:2] x軸の表示範囲を0~2に固定
set yrange [0:2] y軸の表示範囲を0~2に固定
set zrange [0:1] z軸の表示範囲を0~1に固定
set view 0,0 真上から見下ろす
set size 1,1 グラフの縦横比を1:1
unset contour 2次元等高線を表示
unset surface 3次元で等値面を表示しない
set pm3d カラー表示しない
以下でファイルを読み込み,3次元表示
splot 'T.txt' with line](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-41-2048.jpg)


![#define dxdxdydy (dxdx*dydy)
#define dxdy2 (2.0*(dxdx+dydy))
void sor(double *f, double *g){
int ite_SOR=0;
double err_n,err_d,err_relative;
double d_f;
int ij,ip1j,im1j,ijm1,ijp1;
do{
err_n = 0.0;
err_d = 0.0;
for(int j=1;j<Ny‐1;j++){
for(int i=1;i<Nx‐1;i++){
ij = i+Nx*j;
ip1j = (i+1)+Nx*(j );
im1j = (i‐1)+Nx*(j );
ijp1 = (i )+Nx*(j+1);
ijm1 = (i )+Nx*(j‐1);
d_f =( (f[im1j]+f[ip1j])/dxdx
+(f[ijm1]+f[ijp1])/dydy
‐(g[ij]) //右辺の影響
)*dxdxdydy/dxdy2 ‐f[ij];
f[ij] += Accel*d_f;
err_n += d_f*d_f;
err_d += f[ij]*f[ij];
}
}
if(err_d<1e‐20)err_d=1.0;
err_relative = sqrt(err_n/err_d);
ite_SOR++;
}while(err_relative > ERR_TOL);
}
CPUプログラム(SOR法)
2015/06/18先端GPGPUシミュレーション工学特論44
poisson.c](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-44-2048.jpg)
![void cg(double *f, double *g){
double err;
int ij,ip1j,im1j,ijm1,ijp1;
double alph,beta,rr,pAp,bb;
double *p = (double *)malloc
(Nx*Ny*sizeof(double));
double *r = (double *)malloc
(Nx*Ny*sizeof(double));
double *Ap = (double *)malloc
(Nx*Ny*sizeof(double));
for(int j=0;j<Ny;j++){
for(int i=0;i<Nx;i++){
ij = i+Nx*j;
p [ij] = 0.0;
r [ij] = 0.0;
Ap[ij] = 0.0;
}
}
alph=0.0;
beta=0.0;
bb = 0.0;
rr = 0.0;
for(int j=1;j<Ny‐1;j++){
for(int i=1;i<Nx‐1;i++){
ij = i+Nx*j;
ip1j = (i+1)+Nx*(j );
im1j = (i‐1)+Nx*(j );
ijp1 = (i )+Nx*(j+1);
ijm1 = (i )+Nx*(j‐1);
r[ij] = g[ij] //右辺の影響
‐( (f[im1j]‐2*f[ij]+f[ip1j])/dxdx
+(f[ijm1]‐2*f[ij]+f[ijp1])/dydy);
rr += r[ij]*r[ij];
bb += g[ij]*g[ij];
}
}
CPUプログラム(共役勾配法)
2015/06/18先端GPGPUシミュレーション工学特論45
poisson.c](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-45-2048.jpg)
![do{
for(int j=0;j<Ny;j++){
for(int i=0;i<Nx;i++){
ij = i+Nx*j;
p [ij] = r[ij] + beta*p[ij];
}
}
pAp = 0.0;
for(int j=1;j<Ny‐1;j++){
for(int i=1;i<Nx‐1;i++){
ij = i+Nx*j;
ip1j = (i+1)+Nx*(j );
im1j = (i‐1)+Nx*(j );
ijp1 = (i )+Nx*(j+1);
ijm1 = (i )+Nx*(j‐1);
//右辺の影響は入らない
Ap[ij] = (p[im1j]‐2*p[ij]+p[ip1j])/dxdx
+(p[ijm1]‐2*p[ij]+p[ijp1])/dydy;
pAp += p[ij]*Ap[ij];
}
}
alph = rr/pAp;
rr = 0.0;
for(int j=0;j<Ny;j++){
for(int i=0;i<Nx;i++){
ij = i+Nx*j;
f[ij] = f[ij] + alph* p[ij];
r[ij] = r[ij] ‐ alph*Ap[ij];
rr += r[ij]*r[ij];
}
}
err = sqrt(rr/bb);
beta = rr/(alph*pAp);
}while(err > ERR_TOL);
}
CPUプログラム(共役勾配法)
2015/06/18先端GPGPUシミュレーション工学特論46
poisson.c](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-46-2048.jpg)
![CPUプログラム
右辺(ソース項)g
境界条件
for(i=0;i<Nx;i++){
for(j=0;j<Ny;j++){
x = (double)i*dx;
y = (double)j*dy;
g[i*Ny+j] = 2.0*sin(2.0*M_PI*x/Lx)
*sin(2.0*M_PI*y/Ly);
}
}
先端GPGPUシミュレーション工学特論47 2015/06/18
yxg sinsin2
0sinsin22
yxf
2
2
g
2−2](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-47-2048.jpg)
![#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#define Lx (2.0*M_PI)
#define Ly Lx
#define Nx 11
#define Ny Ny
#define dx (Lx/(Nx‐1))
#define dy dx
#define dxdx (dx*dx)
#define dydy (dy*dy)
#define dxdxdydy (dxdx*dydy)
#define dxdy2 (2.0*(dxdx+dydy))
#define Nbytes (Nx*Ny*sizeof(double))
#define ERR_TOL 1e‐12
#define Accel 1.0
void sor(double *f,double *g);
void cg(double *f,double *g);
void init(double *f,double *g){
for(int j=0;j<Ny;j++){
for(int i=0;i<Nx;i++){
g[i+Nx*j] = 2.0*sin(2.0*M_PI*x/Lx)
*sin(2.0*M_PI*y/Ly);
f[i+Nx*j] = 0.0;
}
}
}
int main(void){
double *f, *g;
f = (double *)malloc(Nbytes);
g = (double *)malloc(Nbytes);
init(f,g);
sor(f,g)
//cg(f,g);
return 0;
}
CPUプログラム(メイン・初期化)
2015/06/18先端GPGPUシミュレーション工学特論48
poisson.c](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-48-2048.jpg)
![void sor(double *f, double *g){
int ite_SOR=0;
double err_n,err_d,err_relative;
double d_f;
int ij,ip1j,im1j,ijm1,ijp1;
//境界値は全て0固定なので何もしない
do{
err_n = 0.0;
err_d = 0.0;
for(int j=1;j<Ny‐1;j++){
for(int i=1;i<Nx‐1;i++){
ij = i+Nx*j;
ip1j = (i+1)+Nx*(j );
im1j = (i‐1)+Nx*(j );
ijp1 = (i )+Nx*(j+1);
ijm1 = (i )+Nx*(j‐1);
d_f =( (f[im1j]+f[ip1j])/dxdx
+(f[ijm1]+f[ijp1])/dydy
‐(g[ij])
)*dxdxdydy/dxdy2 ‐f[ij];
f[ij] += Accel*d_f;
err_n += d_f*d_f;
err_d += f[ij]*f[ij];
}
}
if(err_d<1e‐20)err_d=1.0;
err_relative = sqrt(err_n/err_d);
ite_SOR++;
}while(err_relative > ERR_TOL);
}
CPUプログラム(SOR法)
2015/06/18先端GPGPUシミュレーション工学特論49
poisson.c](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-49-2048.jpg)
![void cg(double *f, double *g){
double err;
int ij,ip1j,im1j,ijm1,ijp1;
double *p,*r,*Ap;
double alph,beta,rr,pAp,bb;
p = (double *)malloc(Nbytes);
r = (double *)malloc(Nbytes);
Ap = (double *)malloc(Nbytes);
for(int j=0;j<Ny;j++){
for(int i=0;i<Nx;i++){
ij = i+Nx*j;
p [ij] = 0.0;
r [ij] = 0.0;
Ap[ij] = 0.0;
}
}
alph=0.0;
beta=0.0;
//境界値は全て0固定なので何もしない
bb = 0.0;
rr = 0.0;
for(int j=1;j<Ny‐1;j++){
for(int i=1;i<Nx‐1;i++){
ij = i+Nx*j;
ip1j = (i+1)+Nx*(j );
im1j = (i‐1)+Nx*(j );
ijp1 = (i )+Nx*(j+1);
ijm1 = (i )+Nx*(j‐1);
r[ij] = g[ij]‐((f[im1j]‐2*f[ij]+f[ip1j])/dxdx
+(f[ijm1]‐2*f[ij]+f[ijp1])/dydy
);
rr += r[ij]*r[ij];
bb += g[ij]*g[ij];
}
}
CPUプログラム(共役勾配法)
2015/06/18先端GPGPUシミュレーション工学特論50
poisson.c](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-50-2048.jpg)
![do{
for(int j=0;j<Ny;j++){
for(int i=0;i<Nx;i++){
ij = i+Nx*j;
p [ij] = r[ij] + beta*p[ij];
}
}
pAp = 0.0;
for(int j=1;j<Ny‐1;j++){
for(int i=1;i<Nx‐1;i++){
ij = i+Nx*j;
ip1j = (i+1)+Nx*(j );
im1j = (i‐1)+Nx*(j );
ijp1 = (i )+Nx*(j+1);
ijm1 = (i )+Nx*(j‐1);
Ap[ij] = (p[im1j]‐2*p[ij]+p[ip1j])/dxdx
+(p[ijm1]‐2*p[ij]+p[ijp1])/dydy;
pAp += p[ij]*Ap[ij];
}
}
alph = rr/pAp;
rr = 0.0;
for(int j=0;j<Ny;j++){
for(int i=0;i<Nx;i++){
ij = i+Nx*j;
f[ij] = f[ij] + alph* p[ij];
r[ij] = r[ij] ‐ alph*Ap[ij];
rr += r[ij]*r[ij];
}
}
err = sqrt(rr/bb);
beta = rr/(alph*pAp);
}while(err > ERR_TOL);
}
CPUプログラム(共役勾配法)
2015/06/18先端GPGPUシミュレーション工学特論51
poisson.c](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-51-2048.jpg)
![計算結果
2015/06/18先端GPGPUシミュレーション工学特論52
前回授業で用いたgnuplotのanim_2d.gplを流用
して2次元分布を確認
set xrange [0:2*pi] x軸の表示範囲を0~2に固定
set yrange [0:2*pi] y軸の表示範囲を0~2に固定
set zrange [‐1:1] z軸の表示範囲を‐1~1に固定
set view 0,0 真上から見下ろす
set size 1,1 グラフの縦横比を1:1
set contour 2次元等高線を表示
unset surface 3次元で等値面を表示しない
unset pm3d カラー表示しない
set cntrparam levels incremental ‐1,0.1,1
等高線を0から1まで0.1刻みに設定
以下でファイルを読み込み,3次元表示
splot 'f.txt' with line](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-52-2048.jpg)
![計算結果
2015/06/18先端GPGPUシミュレーション工学特論53
前回授業で用いたgnuplotのanim_2d.gplを流用
して2次元分布を確認
set xrange [0:2*pi] x軸の表示範囲を0~2に固定
set yrange [0:2*pi] y軸の表示範囲を0~2に固定
set zrange [‐1:1] z軸の表示範囲を‐1~1に固定
set view 0,0 真上から見下ろす
set size 1,1 グラフの縦横比を1:1
unset contour 2次元等高線を表示
unset surface 3次元で等値面を表示しない
set pm3d カラー表示しない
以下でファイルを読み込み,3次元表示
splot 'f.txt' with line](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-53-2048.jpg)

![void cg(double *f, double *g){
double err;
int ij,ip1j,im1j,ijm1,ijp1;
double *p,*r,*Ap;
double alph,beta,rr,pAp,bb;
p = (double *)malloc(Nbytes);
r = (double *)malloc(Nbytes);
Ap = (double *)malloc(Nbytes);
for(int j=0;j<Ny;j++){
for(int i=0;i<Nx;i++){
ij = i+Nx*j;
p [ij] = 0.0;
r [ij] = 0.0;
Ap[ij] = 0.0;
}
}
alph=0.0;
beta=0.0;
共役勾配法の並列化・GPU移植
2015/06/18先端GPGPUシミュレーション工学特論55
1スレッドが配列の1要素に0を代入
容易に並列化・GPU移植可能](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-55-2048.jpg)
![bb = 0.0;
rr = 0.0;
for(int j=1;j<Ny‐1;j++){
for(int i=1;i<Nx‐1;i++){
ij = i+Nx*j;
ip1j = (i+1)+Nx*(j );
im1j = (i‐1)+Nx*(j );
ijp1 = (i )+Nx*(j+1);
ijm1 = (i )+Nx*(j‐1);
r[ij] = g[ij]‐((f[im1j]‐2*f[ij]+f[ip1j])/dxdx
+(f[ijm1]‐2*f[ij]+f[ijp1])/dydy
);
rr += r[ij]*r[ij];
bb += g[ij]*g[ij];
}
}
共役勾配法の並列化・GPU移植
2015/06/18先端GPGPUシミュレーション工学特論56
残差を計算するカーネルと内積を計算する
カーネルに分離
・残差の計算には拡散方程式のカーネル
・内積の計算は総和計算のカーネル
を流用
容易ではないが,これまでの知識で並列
化・GPU移植可能](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-56-2048.jpg)
![do{
for(int j=0;j<Ny;j++){
for(int i=0;i<Nx;i++){
ij = i+Nx*j;
p [ij] = r[ij] + beta*p[ij];
}
}
共役勾配法の並列化・GPU移植
2015/06/18先端GPGPUシミュレーション工学特論57
ベクトル和と同様に1スレッドが配列の1要素
の計算を実行
容易に並列化・GPU移植可能](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-57-2048.jpg)
![pAp = 0.0;
for(int j=1;j<Ny‐1;j++){
for(int i=1;i<Nx‐1;i++){
ij = i+Nx*j;
ip1j = (i+1)+Nx*(j );
im1j = (i‐1)+Nx*(j );
ijp1 = (i )+Nx*(j+1);
ijm1 = (i )+Nx*(j‐1);
Ap[ij] = (p[im1j]‐2*p[ij]+p[ip1j])/dxdx
+(p[ijm1]‐2*p[ij]+p[ijp1])/dydy;
pAp += p[ij]*Ap[ij];
}
}
alph = rr/pAp;
共役勾配法の並列化・GPU移植
2015/06/18先端GPGPUシミュレーション工学特論58
残差を計算するカーネルと内積を計算する
カーネルに分離
・残差の計算には拡散方程式のカーネル
・内積の計算は総和計算のカーネル
を流用
容易ではないが,これまでの知識で並列
化・GPU移植可能](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-58-2048.jpg)
![rr = 0.0;
for(int j=0;j<Ny;j++){
for(int i=0;i<Nx;i++){
ij = i+Nx*j;
f[ij] = f[ij] + alph* p[ij];
r[ij] = r[ij] ‐ alph*Ap[ij];
rr += r[ij]*r[ij];
}
}
err = sqrt(rr/bb);
beta = rr/(alph*pAp);
}while(err > ERR_TOL);
}
共役勾配法の並列化・GPU移植
2015/06/18先端GPGPUシミュレーション工学特論59
ベクトル和と同様に1スレッドが配列の1要素
の計算を実行
容易に並列化・GPU移植可能](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-59-2048.jpg)


![SOR法の並列化
2015/06/18先端GPGPUシミュレーション工学特論62
SOR法の処理の手順
更新手順に依存性が存在
Jacobi法なら依存性問題は回
避できるが収束が遅すぎる
並列化の影響で反復毎に更新
順序が変化すると収束が保証さ
れない
配列順序・計算順序の並び替え
(オーダリング)を導入
f[]
i
j
22
22
2
)1(
1,
)(
1,
2
)1(
,1
)(
,1
.
)1(
,
2
ΔyΔx
ΔyΔx
Δy
ff
Δx
ff
g
f
m
ji
m
ji
m
ji
m
ji
ji
m
ji
](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-62-2048.jpg)
![Red-Blackオーダリング
2015/06/18先端GPGPUシミュレーション工学特論63
更新順序を2段階に分離
赤色の要素を参照し,黒色の要素全てを更新
黒色の要素を参照し,赤色の要素全てを更新
f[]
i
j
i
j
i
fr[] fb[]](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-63-2048.jpg)
![Red-Blackオーダリング
2015/06/18先端GPGPUシミュレーション工学特論64
更新順序を2段階に分離
赤色の要素を参照し,黒色の要素全てを更新
黒色の要素を参照し,赤色の要素全てを更新
f[]
i
j
fr[]
i
j
fb[]
i](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-64-2048.jpg)

![void rbsor(double *f, double *g){
int ite_SOR=0;
double err_n,err_d,err_relative;
double d_f;
int ij,ip1j,im1j,ijm1,ijp1;
do{
err_n = 0.0;
err_d = 0.0;
//赤色要素を計算
for(int j=1;j<Ny‐1;j++){
for(int i=1+j%2;i<Nx‐1;i+=2){
ij = i+Nx*j;
ip1j = (i+1)+Nx*(j );
im1j = (i‐1)+Nx*(j );
ijp1 = (i )+Nx*(j+1);
ijm1 = (i )+Nx*(j‐1);
d_f =( (f[im1j]+f[ip1j])/dxdx
+(f[ijm1]+f[ijp1])/dydy
‐(g[ij])
)*dxdxdydy/dxdy2 ‐f[ij];
f[ij] += Accel*d_f;
err_n += d_f*d_f;
err_d += f[ij]*f[ij];
}
}
CPUプログラム(RB-SOR法)
2015/06/18先端GPGPUシミュレーション工学特論66
poisson.c](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-66-2048.jpg)
![CPUプログラム(RB-SOR法)
2015/06/18先端GPGPUシミュレーション工学特論67
poisson.c
//黒色要素を計算
for(int j=1;j<Ny‐1;j++){
for(int i=1+(j‐1)%2;i<Nx‐1;i+=2){
ij = i+Nx*j;
ip1j = (i+1)+Nx*(j );
im1j = (i‐1)+Nx*(j );
ijp1 = (i )+Nx*(j+1);
ijm1 = (i )+Nx*(j‐1);
d_f =( (f[im1j]+f[ip1j])/dxdx
+(f[ijm1]+f[ijp1])/dydy
‐(g[ij])
)*dxdxdydy/dxdy2 ‐f[ij];
f[ij] += Accel*d_f;
err_n += d_f*d_f;
err_d += f[ij]*f[ij];
}
}
if(err_d<1e‐20)err_d=1.0;
err_relative = sqrt(err_n/err_d);
ite_SOR++;
}while(err_relative > ERR_TOL);
}](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-67-2048.jpg)
![赤色要素の計算
2015/06/18先端GPGPUシミュレーション工学特論68
j=1(奇数)のときに計算するiは2,4,6
j=2(偶数)のときに計算するiは1,3,5
計算の範囲は0<i<Nx‐1,0<j<Ny‐1
f[]
0 1 2 3 4 5 6 7
0 1 2 3 4 5 6 7
iの最小値は1,jが奇数の時+1,偶数の時+0
jを2で割った剰余を利用してiの開始点を決定
i=1+j%2
for(int j=1;j<Ny‐1;j++){
for(int i=1+j%2;i<Nx‐1;i+=2){
ij = i+Nx*j;
ip1j = (i+1)+Nx*(j );
im1j = (i‐1)+Nx*(j );
ijp1 = (i )+Nx*(j+1);
ijm1 = (i )+Nx*(j‐1);
d_f =( (f[im1j]+f[ip1j])/dxdx
+(f[ijm1]+f[ijp1])/dydy
‐(g[ij])
)*dxdxdydy/dxdy2 ‐f[ij];
f[ij] += Accel*d_f;
}
}
剰余(j%2)をアンド演算(j&1)に置き換えると実行速度はどうなる?](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-68-2048.jpg)
![黒色要素の計算
2015/06/18先端GPGPUシミュレーション工学特論69
j=1(奇数)のときに計算するiは1,3,5
j=2(偶数)のときに計算するiは2,4,6
計算の範囲は0<i<Nx‐1,0<j<Ny‐1
for(int j=1;j<Ny‐1;j++){
for(int i=1+(j+1)%2;i<Nx‐1;i+=2){
ij = i+Nx*j;
ip1j = (i+1)+Nx*(j );
im1j = (i‐1)+Nx*(j );
ijp1 = (i )+Nx*(j+1);
ijm1 = (i )+Nx*(j‐1);
d_f =( (f[im1j]+f[ip1j])/dxdx
+(f[ijm1]+f[ijp1])/dydy
‐(g[ij])
)*dxdxdydy/dxdy2 ‐f[ij];
f[ij] += Accel*d_f;
}
}
f[]
0 1 2 3 4 5 6 7
0 1 2 3 4 5 6 7
iの最小値は1,jが奇数の時+0,偶数の時+1
jを2で割った剰余を利用してiの開始点を決定
i=1+(j+1)%2 (=2‐j%2とも書ける)](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-69-2048.jpg)

![#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#define Lx (2.0*M_PI)
#define Ly (2.0*M_PI)
#define Nx 256
#define Ny Nx
#define Nbytes (Nx*Ny*sizeof(double))
#define dx (Lx/(Nx‐1))
#define dy (Ly/(Ny‐1))
#define THREADX 16
#define THREADY 16
#define BLOCKX (Nx/THREADX)
#define BLOCKY (Ny/THREADY)
void output(double *value, char *name);
#include"rbsor.cu"
__global__ void init(double *f, double *g){
int i=blockIdx.x*blockDim.x+threadIdx.x;
int j=blockIdx.y*blockDim.y+threadIdx.y;
int ij = i+Nx*j;
double x = (double)i*dx;
double y = (double)j*dy;
g[ij] = 2.0*sin(2.0*M_PI*x/Lx)
*sin(2.0*M_PI*y/Ly);
f[ij] = 0.0;
}
GPUプログラム(メイン)
2015/06/18先端GPGPUシミュレーション工学特論71
poisson.cu](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-71-2048.jpg)



![__global__ void computeRed(double *f,double *g, int *converged){
int j = blockIdx.y* blockDim.y + threadIdx.y;
int i = blockIdx.x*(blockDim.x*2) + threadIdx.x*2 + (j+1)%2;
int ij = i+Nx*j;
int ip1j = (i+1)+Nx*(j );
int im1j = (i‐1)+Nx*(j );
int ijp1 = (i )+Nx*(j+1);
int ijm1 = (i )+Nx*(j‐1);
double d_f;
if(0<i && i<Nx‐1 && 0<j && j<Ny‐1){
d_f =( (f[im1j]+f[ip1j])/dxdx
+(f[ijm1]+f[ijp1])/dydy
‐(g[ij])
)*dxdxdydy/dxdy2 ‐f[ij];
f[ij] += Accel*d_f;
if(abs(d_f) > ERR_TOL) *converged = 0;
}
}
RB-SOR法(赤色要素の計算)
2015/06/18先端GPGPUシミュレーション工学特論75
rbsor.cu](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-75-2048.jpg)
![__global__ void computeBlack(double *f,double *g, int *converged){
int j = blockIdx.y* blockDim.y + threadIdx.y;
int i = blockIdx.x*(blockDim.x*2) + threadIdx.x*2 + (j)%2;
int ij = i+Nx*j;
int ip1j = (i+1)+Nx*(j );
int im1j = (i‐1)+Nx*(j );
int ijp1 = (i )+Nx*(j+1);
int ijm1 = (i )+Nx*(j‐1);
double d_f;
if(0<i && i<Nx‐1 && 0<j && j<Ny‐1){
d_f =( (f[im1j]+f[ip1j])/dxdx
+(f[ijm1]+f[ijp1])/dydy
‐(g[ij])
)*dxdxdydy/dxdy2 ‐f[ij];
f[ij] += Accel*d_f;
if(abs(d_f) > ERR_TOL) *converged = 0;
}
}
RB-SOR法(黒色要素の計算)
2015/06/18先端GPGPUシミュレーション工学特論76
rbsor.cu](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-76-2048.jpg)
![並列度の指定
2015/06/18先端GPGPUシミュレーション工学特論77
初期化
1スレッドが一つの配列要素を計算
f[]
0 1 2 3 4 5 6 7
0 1 2 3 4 5 6 7
#define THREADX 16
#define THREADY 16
#define BLOCKX (Nx/THREADX)
#define BLOCKY (Ny/THREADY)
Thread = dim3(THREADX,THREADY,1);
Block = dim3(BLOCKX,BLOCKY,1);
init<<<Block, Thread >>>
(dev_f,dev_g);
i=blockIdx.x*blockDim.x+threadIdx.x;
j=blockIdx.y*blockDim.y+threadIdx.y;](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-77-2048.jpg)
![並列度の指定
2015/06/18先端GPGPUシミュレーション工学特論78
RB‐SOR法
i方向の計算に必要なスレッド数は初期化の1/2
必要なブロック数は同じ
f[]
0 1 2 3 4 5 6 7
0 1 2 3 4 5 6 7
#define SORTx (THREADX/2)
#define SORTy (THREADY)
#define SORBx (BLOCKX)
#define SORBy (BLOCKY)
dim3 Block, Thread;
Thread = dim3(SORTx,SORTy,1);
Block = dim3(SORBx,SORBy,1);
computeRed<<<Block, Thread>>>
(f,g,converged);](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-78-2048.jpg)
![並列度の指定
2015/06/18先端GPGPUシミュレーション工学特論79
RB‐SOR法
スレッド番号と配列添字をどう対応させるか
j方向は変更無し,i方向のみ変化
f[]
0 1 2 3 4 5 6 7
0 1 2 3 4 5 6 7
#define SORTx (THREADX/2)
#define SORTy (THREADY)
#define SORBx (BLOCKX)
#define SORBy (BLOCKY)
dim3 Block, Thread;
Thread = dim3(SORTx,SORTy,1);
Block = dim3(SORBx,SORBy,1);
computeRed<<<Block, Thread>>>
(f,g,converged);](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-79-2048.jpg)
![ストライドアクセス時の配列添字の決定
N=12, <<<3, 2>>>で実行
2015/06/18先端GPGPUシミュレーション工学特論80
c[i]
a[i]
b[i]
0 1 0
+ + + +
1
gridDim.x=3
blockDim.x=2
0 1
+ +
blockDim.x=2 blockDim.x=2
blockIdx.x=0 blockIdx.x=1 blockIdx.x=2
threadIdx.x=
i= 0 1 2 3 4 5 6 7 8 9 10 11](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-80-2048.jpg)
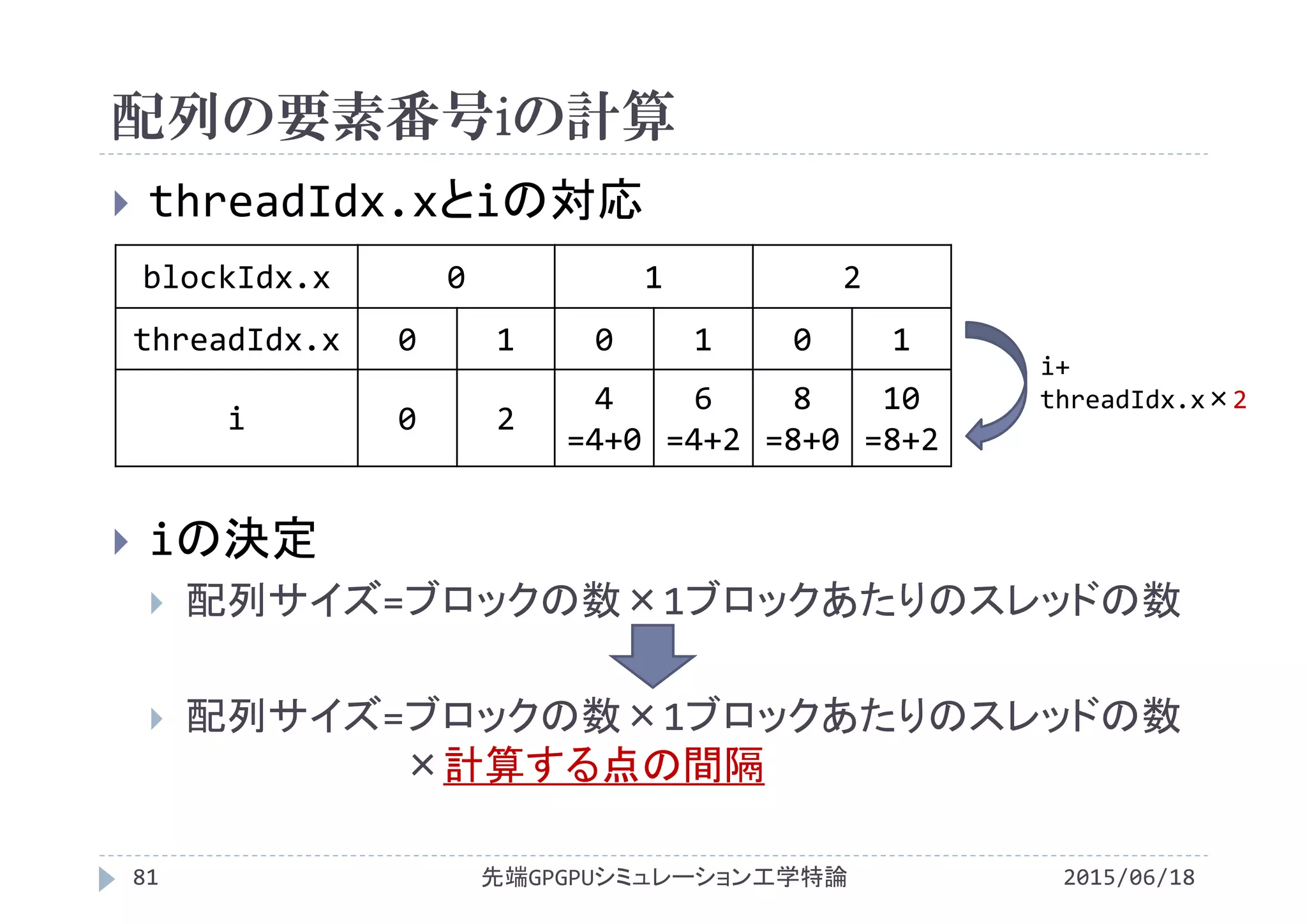
![ストライドアクセス時の配列添字の決定
N=12, <<<3, 2>>>で実行
2015/06/18先端GPGPUシミュレーション工学特論82
c[i]
a[i]
b[i]
0 1 0
+ + + +
1
gridDim.x=3
blockDim.x=2
0 1
+ +
blockDim.x=2 blockDim.x=2
blockIdx.x=0 blockIdx.x=1 blockIdx.x=2
threadIdx.x=
i= 0 1 2 3 4 5 6 7 8 9 10 11
= blockIdx.x*(blockDim.x*2) + threadIdx.x*2
計算する点の間隔 計算する点の間隔](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-82-2048.jpg)
![並列度の指定
2015/06/18先端GPGPUシミュレーション工学特論83
i方向のスレッド番号と配列添字の対応
ストライドアクセス
f[]
0 1 2 3 4 5 6 7
0 1 2 3 4 5 6 7
j = blockIdx.y* blockDim.y + threadIdx.y;
i = blockIdx.x*(blockDim.x*2) + threadIdx.x*2;
j](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-83-2048.jpg)
![並列度の指定
2015/06/18先端GPGPUシミュレーション工学特論84
i方向のスレッド番号と配列添字の対応
ストライドアクセス
開始点の変化(jが奇数のとき0開始,偶数のときは1開始)
f[]
0 1 2 3 4 5 6 7
0 1 2 3 4 5 6 7
+0
+1
+0
+1
j
(j+1)%2
j = blockIdx.y* blockDim.y + threadIdx.y;
i = blockIdx.x*(blockDim.x*2) + threadIdx.x*2
+ (j+1)%2;](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-84-2048.jpg)
![並列度の指定
2015/06/18先端GPGPUシミュレーション工学特論85
RB‐SOR法
スレッド番号と配列添字をどう対応させるか
j方向は変更無し,i方向のみ変化
f[]
0 1 2 3 4 5 6 7
0 1 2 3 4 5 6 7
#define SORTx (THREADX/2)
#define SORTy (THREADY)
#define SORBx (BLOCKX)
#define SORBy (BLOCKY)
dim3 Block, Thread;
Thread = dim3(SORTx,SORTy,1);
Block = dim3(SORBx,SORBy,1);
computeBlack<<<Block, Thread>>>
(f,g,converged);](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-85-2048.jpg)
![並列度の指定
2015/06/18先端GPGPUシミュレーション工学特論86
i方向のスレッド番号と配列添字の対応
ストライドアクセス
f[]
0 1 2 3 4 5 6 7
0 1 2 3 4 5 6 7
j = blockIdx.y* blockDim.y + threadIdx.y;
i = blockIdx.x*(blockDim.x*2) + threadIdx.x*2;
j](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-86-2048.jpg)
![並列度の指定
2015/06/18先端GPGPUシミュレーション工学特論87
i方向のスレッド番号と配列添字の対応
ストライドアクセス
開始点の変化(jが奇数のとき0開始,偶数のときは1開始)
f[]
0 1 2 3 4 5 6 7
0 1 2 3 4 5 6 7
+1
+0
+1
+0
j
(j)%2
j = blockIdx.y* blockDim.y + threadIdx.y;
i = blockIdx.x*(blockDim.x*2) + threadIdx.x*2
+ (j)%2;
剰余(j%2)をアンド演算(j&1)に置き換える
と実行速度はどう変わるだろうか](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-87-2048.jpg)

![配列の分離
2015/06/18先端GPGPUシミュレーション工学特論89
色ごとに格納する配列を区別
ストライドアクセスを排除
元の配列を分離,出力時に結合するカーネルを作成
f[]
i
j
fr[]
i
j
fb[]
i](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-89-2048.jpg)


![__global__ void split
(double *f, double *fr,double *fb){
__shared__ double sf[THREADX][THREADY];
__shared__ double sfrb[THREADX][THREADY];
int tx = threadIdx.x;
int ty = threadIdx.y;
int j = blockIdx.y* blockDim.y + threadIdx.y;
int i = blockIdx.x*(blockDim.x*2) + threadIdx.x;
int ij = i+Nx*j;
sf[tx][ty] = f[ij];
__syncthreads();
i = blockIdx.x*(blockDim.x*2) + threadIdx.x
+ blockDim.x;
ij = i+Nx*j;
sf[tx+blockDim.x][ty] = f[ij];
__syncthreads();
sfrb[tx ][ty]
= sf[tx*2+(j+1)%2][ty];
sfrb[tx+blockDim.x][ty]
= sf[tx*2+(j )%2][ty];
__syncthreads();
i = blockIdx.x*blockDim.x + threadIdx.x;
ij= i+Nx/2*j;
fr[ij] = sfrb[tx ][ty];
fb[ij] = sfrb[tx+blockDim.x][ty];
}
配列を分離するRB-SOR法(配列分離)
2015/06/18先端GPGPUシミュレーション工学特論92
rbsor_split.cu](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-92-2048.jpg)
![配列の分離
2015/06/18先端GPGPUシミュレーション工学特論93
共有メモリ上に配列を宣言
グローバルメモリからコピーするための配列
並び替え後のデータを格納する配列
f[]__shared__ double sf[THREADX][THREADY];
__shared__ double sfrb[THREADX][THREADY];
int tx = threadIdx.x;
int ty = threadIdx.y;
int j = blockIdx.y* blockDim.y + threadIdx.y;
int i = blockIdx.x*(blockDim.x*2) + threadIdx.x;
int ij = i+Nx*j;
sf[tx][ty] = f[ij];
__syncthreads();
sf[][]
sfrb[][]](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-93-2048.jpg)
![配列の分離
2015/06/18先端GPGPUシミュレーション工学特論94
共有メモリ上に配列を宣言
グローバルメモリからコピーするための配列
並び替え後のデータを格納する配列
グローバルメモリから共有メモリにコ
ピーして同期を取る
f[]__shared__ double sf[THREADX][THREADY];
__shared__ double sfrb[THREADX][THREADY];
int tx = threadIdx.x;
int ty = threadIdx.y;
int j = blockIdx.y* blockDim.y + threadIdx.y;
int i = blockIdx.x*(blockDim.x*2) + threadIdx.x;
int ij = i+Nx*j;
sf[tx][ty] = f[ij];
__syncthreads();
sf[][]
0 1 2 3
0 1 2 3](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-94-2048.jpg)
![配列の分離
2015/06/18先端GPGPUシミュレーション工学特論95
i方向の位置を変更してさらにグロー
バルメモリから共有メモリにコピー
f[]
i = blockIdx.x*(blockDim.x*2) + threadIdx.x
+ blockDim.x;
ij = i+Nx*j;
sf[tx+blockDim.x][ty] = f[ij];
__syncthreads();
sf[][]
0 1 2 3
0 1 2 3](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-95-2048.jpg)
![配列の分離
2015/06/18先端GPGPUシミュレーション工学特論96
共有メモリ上でストライドアクセスして
赤色要素と黒色要素を並び替え
jの位置に応じてiの位置を変更
f[]
sfrb[tx ][ty]
= sf[tx*2+(j+1)%2][ty];
sf[][]
0 1 2 3
0 1 2 3
sfrb[][]
二つ目の共有メモリsfrb[][]を利用しない
と性能はどのように変化するだろうか?](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-96-2048.jpg)
![配列の分離
2015/06/18先端GPGPUシミュレーション工学特論97
共有メモリ上でストライドアクセスして
赤色要素と黒色要素を並び替え
jの位置に応じてiの位置を変更
並び替え後の配列に赤色要素を書込
f[]
sfrb[tx ][ty]
= sf[tx*2+(j+1)%2][ty];
sf[][]
0 1 2 3
0 1 2 3
sfrb[][]
+0
+1
+0
+1
(j+1)%2
0 1 2 3
0 1 2 3
二つ目の共有メモリsfrb[][]を利用しない
と性能はどのように変化するだろうか?](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-97-2048.jpg)
![配列の分離
2015/06/18先端GPGPUシミュレーション工学特論98
共有メモリ上でストライドアクセスして
赤色要素と黒色要素を並び替え
jの位置に応じてiの位置を変更
f[]
sfrb[tx+blockDim.x][ty]
= sf[tx*2+(j )%2][ty];
__syncthreads();
sf[][]
0 1 2 3
0 1 2 3
sfrb[][]
0 1 2 3
0 1 2 3
二つ目の共有メモリsfrb[][]を利用しない
と性能はどのように変化するだろうか?](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-98-2048.jpg)
![配列の分離
2015/06/18先端GPGPUシミュレーション工学特論99
共有メモリ上でストライドアクセスして
赤色要素と黒色要素を並び替え
jの位置に応じてiの位置を変更
並び替え後の配列に黒色要素を書込
f[]
sfrb[tx+blockDim.x][ty]
= sf[tx*2+(j )%2][ty];
__syncthreads();
sf[][]
0 1 2 3
0 1 2 3
sfrb[][]
+1
+0
+1
+0
(j )%2
0 1 2 3
0 1 2 3
二つ目の共有メモリsfrb[][]を利用しない
と性能はどのように変化するだろうか?](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-99-2048.jpg)
![配列の分離
2015/06/18先端GPGPUシミュレーション工学特論100
共有メモリの赤色,黒色要素を分離し
た配列に書込
各配列にコアレスアクセスで書込
i = blockIdx.x*blockDim.x + threadIdx.x;
ij= i+Nx/2*j;
fr[ij] = sfrb[tx ][ty];
fb[ij] = sfrb[tx+blockDim.x][ty];
fr[] fb[]
sfrb[][]
0 1 2 3
0 1 2 3
二つ目の共有メモリsfrb[][]を利用しない
と性能はどのように変化するだろうか?](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-100-2048.jpg)
![配列の分離
2015/06/18先端GPGPUシミュレーション工学特論101
共有メモリの赤色,黒色要素を分離し
た配列に書込
各配列にコアレスアクセスで書込
i = blockIdx.x*blockDim.x + threadIdx.x;
ij= i+Nx/2*j;
fr[ij] = sfrb[tx ][ty];
fb[ij] = sfrb[tx+blockDim.x][ty];
fr[] fb[]
sfrb[][]
0 1 2 3
0 1 2 3
二つ目の共有メモリsfrb[][]を利用しない
と性能はどのように変化するだろうか?](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-101-2048.jpg)
![__global__ void merge
(double *f, double *fr,double *fb){
__shared__ double sf[THREADX][THREADY];
__shared__ double sfrb[THREADX][THREADY];
int tx = threadIdx.x;
int ty = threadIdx.y;
int j = blockIdx.y*blockDim.y + threadIdx.y;
int i = blockIdx.x*blockDim.x + threadIdx.x;
int ij = i+Nx/2*j;
sfrb[tx ][ty] = fr[ij];
sfrb[tx+blockDim.x][ty] = fb[ij];
__syncthreads();
sf[tx*2+(j+1)%2][ty]
= sfrb[tx ][ty];
sf[tx*2+(j )%2][ty]
= sfrb[tx+blockDim.x][ty];
__syncthreads();
i = blockIdx.x*(blockDim.x*2) + threadIdx.x;
ij= i+Nx*j;
f[ij] = sf[tx ][ty];
i = blockIdx.x*(blockDim.x*2) + threadIdx.x
+ blockDim.x;
ij= i+Nx*j;
f[ij] = sf[tx+blockDim.x][ty];
}
配列を分離するRB-SOR法(配列結合)
2015/06/18先端GPGPUシミュレーション工学特論102
rbsor_split.cu](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-102-2048.jpg)
![配列の結合
2015/06/18先端GPGPUシミュレーション工学特論103
赤色要素をグローバルメモリから読み
込み,共有メモリへ書込
コアレスアクセスで書込
__shared__ double sf[THREADX][THREADY];
__shared__ double sfrb[THREADX][THREADY];
int tx = threadIdx.x;
int ty = threadIdx.y;
int j = blockIdx.y*blockDim.y + threadIdx.y;
int i = blockIdx.x*blockDim.x + threadIdx.x;
sfrb[tx ][ty] = fr[ij];
sfrb[tx+blockDim.x][ty] = fb[ij];
__syncthreads();
fr[] fb[]
sfrb[][]
0 1 2 3
0 1 2 3
二つ目の共有メモリsfrb[][]を利用しない
と性能はどのように変化するだろうか?](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-103-2048.jpg)
![配列の結合
2015/06/18先端GPGPUシミュレーション工学特論104
黒色要素をグローバルメモリから読み
込み,共有メモリへ書込
コアレスアクセスで書込
__shared__ double sf[THREADX][THREADY];
__shared__ double sfrb[THREADX][THREADY];
int tx = threadIdx.x;
int ty = threadIdx.y;
int j = blockIdx.y*blockDim.y + threadIdx.y;
int i = blockIdx.x*blockDim.x + threadIdx.x;
sfrb[tx ][ty] = fr[ij];
sfrb[tx+blockDim.x][ty] = fb[ij];
__syncthreads();
fr[] fb[]
sfrb[][]
0 1 2 3
0 1 2 3
二つ目の共有メモリsfrb[][]を利用しない
と性能はどのように変化するだろうか?](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-104-2048.jpg)
![配列の結合
2015/06/18先端GPGPUシミュレーション工学特論105
並び替え後の配列内の赤色要素を並
び替え前の配列へ書込
jの位置に応じてiの位置を変更
sf[tx*2+(j+1)%2][ty]
= sfrb[tx ][ty];
sfrb[][]
0 1 2 3
0 1 2 3
sf[][]
0 1 2 3
0 1 2 3
二つ目の共有メモリsfrb[][]を利用しない
と性能はどのように変化するだろうか?](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-105-2048.jpg)
![配列の結合
2015/06/18先端GPGPUシミュレーション工学特論106
並び替え後の配列内の赤色要素を並
び替え前の配列へ書込
jの位置に応じてiの位置を変更
sf[tx*2+(j+1)%2][ty]
= sfrb[tx ][ty];
sfrb[][]
0 1 2 3
0 1 2 3
sf[][]
0 1 2 3
0 1 2 3
+0
+1
+0
+1
(j+1)%2
二つ目の共有メモリsfrb[][]を利用しない
と性能はどのように変化するだろうか?](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-106-2048.jpg)
![配列の結合
2015/06/18先端GPGPUシミュレーション工学特論107
並び替え後の配列内の黒色要素を並
び替え前の配列へ書込
jの位置に応じてiの位置を変更
sf[tx*2+(j )%2][ty]
= sfrb[tx+blockDim.x][ty];
__syncthreads();
sfrb[][]
0 1 2 3
0 1 2 3
sf[][]
0 1 2 3
0 1 2 3
二つ目の共有メモリsfrb[][]を利用しない
と性能はどのように変化するだろうか?](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-107-2048.jpg)
![配列の結合
2015/06/18先端GPGPUシミュレーション工学特論108
並び替え後の配列内の黒色要素を並
び替え前の配列へ書込
jの位置に応じてiの位置を変更
sf[tx*2+(j )%2][ty]
= sfrb[tx+blockDim.x][ty];
__syncthreads();
sfrb[][]
0 1 2 3
0 1 2 3
sf[][]
0 1 2 3
0 1 2 3
+1
+0
+1
+0
(j )%2
二つ目の共有メモリsfrb[][]を利用しない
と性能はどのように変化するだろうか?](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-108-2048.jpg)
![配列の結合
2015/06/18先端GPGPUシミュレーション工学特論109
共有メモリの内容をコアレスアクセスし
て元の配列に書き込み
f[]
i = blockIdx.x*(blockDim.x*2) + threadIdx.x;
ij= i+Nx*j;
f[ij] = sf[tx ][ty];
i = blockIdx.x*(blockDim.x*2) + threadIdx.x
+ blockDim.x;
ij= i+Nx*j;
f[ij] = sf[tx+blockDim.x][ty];
sf[][]
0 1 2 3
0 1 2 3](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-109-2048.jpg)
![配列の結合
2015/06/18先端GPGPUシミュレーション工学特論110
共有メモリの内容をコアレスアクセスし
て元の配列に書き込み
f[] sf[][]
0 1 2 3
0 1 2 3
i = blockIdx.x*(blockDim.x*2) + threadIdx.x;
ij= i+Nx*j;
f[ij] = sf[tx ][ty];
i = blockIdx.x*(blockDim.x*2) + threadIdx.x
+ blockDim.x;
ij= i+Nx*j;
f[ij] = sf[tx+blockDim.x][ty];](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-110-2048.jpg)
![__global__ void computeRed
(double *fr,double *fb, double *gr,double *gb, int *converged){
int j = blockIdx.y*blockDim.y + threadIdx.y;
int i = blockIdx.x*blockDim.x + threadIdx.x;
int ij = i+Nx/2*j;
int iside = i+1‐(j%2)*2;
int isidej = (iside)+Nx/2*(j );
int ijp1 = (i )+Nx/2*(j+1);
int ijm1 = (i )+Nx/2*(j‐1);
double d_f;
if(1‐(j+1)%2<=i && i<Nx/2‐(j+1)%2 && 0<j && j<Ny‐1){
d_f =( (fb[isidej]+fb[ij])/dxdx
+(fb[ijm1 ]+fb[ijp1])/dydy
‐(gr[ij])
)*dxdxdydy/dxdy2 ‐fr[ij];
fr[ij] += Accel*d_f;
if(abs(d_f) > ERR_TOL) *converged = 0;
}
}
配列を分離するRB-SOR法(赤色要素の計算)
2015/06/18先端GPGPUシミュレーション工学特論111
rbsor_split.cu](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-111-2048.jpg)
![__global__ void computeBlack
(double *fb,double *fr, double *gb,double *gr, int *converged){
int j = blockIdx.y*blockDim.y + threadIdx.y;
int i = blockIdx.x*blockDim.x + threadIdx.x;
int ij = i+Nx/2*j;
int iside = i‐1+(j%2)*2;
int isidej = (iside)+Nx/2*(j );
int ijp1 = (i )+Nx/2*(j+1);
int ijm1 = (i )+Nx/2*(j‐1);
double d_f;
if(0+(j+1)%2<=i && i<Nx/2‐(j )%2 && 0<j && j<Ny‐1){
d_f =( (fr[isidej]+fr[ij])/dxdx
+(fr[ijm1 ]+fr[ijp1])/dydy
‐(gb[ij])
)*dxdxdydy/dxdy2 ‐fb[ij];
fb[ij] += Accel*d_f;
if(abs(d_f) > ERR_TOL) *converged = 0;
}
}
配列を分離するRB-SOR法(黒色要素の計算)
2015/06/18先端GPGPUシミュレーション工学特論112
rbsor_split.cu](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-112-2048.jpg)
![並列度の指定
2015/06/18先端GPGPUシミュレーション工学特論113
i方向のスレッド番号と配列添字の対応が単純化
fr[] fb[]
0 1 2 3
0 1 2 3 4 5 6 7
j = blockIdx.y*blockDim.y + threadIdx.y;
i = blockIdx.x*blockDim.x + threadIdx.x;](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-113-2048.jpg)
![配列アクセス
2015/06/18先端GPGPUシミュレーション工学特論114
黒色要素の参照点
jに応じてi方向のどちらを見るかが変化
jが奇数の時はi‐1,偶数の時はi+1
fr[] fb[]
0 1 2 3
0 1 2 3 4 5 6 7
f[]](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-114-2048.jpg)
![配列アクセス
2015/06/18先端GPGPUシミュレーション工学特論115
黒色要素の参照点
jに応じてi方向のどちらを見るかが変化
jが奇数の時はi‐1,偶数の時はi+1
fr[] fb[]
0 1 2 3
0 1 2 3 4 5 6 7
f[]](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-115-2048.jpg)
![配列アクセス
2015/06/18先端GPGPUシミュレーション工学特論116
黒色要素の参照点
jに応じてi方向のどちらを見るかが変化
iside = i+1‐(j%2)*2;
fr[] fb[]
0 1 2 3
0 1 2 3 4 5 6 7
+1
+0
+1
+0
+1
+0
+1
+0
j%2 +1‐j%2*2
‐1
+1
‐1
+1
‐1
+1
‐1
+1](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-116-2048.jpg)
![配列アクセス
2015/06/18先端GPGPUシミュレーション工学特論117
赤色要素の計算範囲
jに応じて変化(jの範囲は変更無し 0<j && j<Ny‐1)
1‐(j+1)%2<=i && i<Nx/2‐(j+1)%2
fr[]
0 1 2 3
0 1 2 3 4 5 6 7
f[]
0
‐1
0
‐1
0
‐1
0
‐1
‐(j+1)%2 1‐(j+1)%2
1<=
0<=
1<=
0<=
1<=
0<=
1<=
0<=
Nx/2‐(j+1)%2
<4
<3
<4
<3
<4
<3
<4
<3](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-117-2048.jpg)
![並列度の指定
2015/06/18先端GPGPUシミュレーション工学特論118
i方向のスレッド番号と配列添字の対応が単純化
fr[] fb[]
0 1 2 3
0 1 2 3 4 5 6 7
j = blockIdx.y*blockDim.y + threadIdx.y;
i = blockIdx.x*blockDim.x + threadIdx.x;](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-118-2048.jpg)
![配列アクセス
2015/06/18先端GPGPUシミュレーション工学特論119
赤色要素の参照点
jに応じてi方向のどちらを見るかが変化
jが奇数の時はi+1,偶数の時はi‐1
fr[] fb[]
0 1 2 3 4 5 6 7
f[]
0 1 2 3](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-119-2048.jpg)
![配列アクセス
2015/06/18先端GPGPUシミュレーション工学特論120
赤色要素の参照点
jに応じてi方向のどちらを見るかが変化
jが奇数の時はi+1,偶数の時はi‐1
fr[] fb[]
0 1 2 3 4 5 6 7
f[]
0 1 2 3](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-120-2048.jpg)
![配列アクセス
2015/06/18先端GPGPUシミュレーション工学特論121
赤色要素の参照点
jに応じてi方向のどちらを見るかが変化
iside = i‐1+(j%2)*2;
fr[] fb[]
0 1 2 3
0 1 2 3 4 5 6 7
‐1+j%2*2
+1
‐1
+1
‐1
+1
‐1
+1
‐1
+1
+0
+1
+0
+1
+0
+1
+0
j%2](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-121-2048.jpg)
![配列アクセス
2015/06/18先端GPGPUシミュレーション工学特論122
黒色要素の計算範囲
jに応じて変化(jの範囲は変更無し 0<j && j<Ny‐1)
0+(j+1)%2<=i && i<Nx/2‐(j )%2
fb[]
0 1 2 3
0 1 2 3 4 5 6 7
f[] 0+(j+1)%2
0<=
1<=
0<=
1<=
0<=
1<=
0<=
1<=
Nx/2‐(j )%2
<3
<4
<3
<4
<3
<4
<3
<4
0
+1
0
+1
0
+1
0
+1
+(j+1)%2](https://image.slidesharecdn.com/advancedgpgpu10-160307060716/75/2015-GPGPU-10-Poisson-122-2048.jpg)