More Related Content
PDF
PDF
PDF
PPTX
PDF
PPTX
PPTX
PDF
What's hot
PDF
PDF
PDF
PDF
PPTX
【DL輪読会】Flamingo: a Visual Language Model for Few-Shot Learning 画像×言語の大規模基盤モ... PDF
PDF
PDF
PDF
PDF
PDF
サポートベクターマシン(SVM)の数学をみんなに説明したいだけの会 PPTX
PPTX
[DL輪読会]Neural Ordinary Differential Equations PDF
PPTX
PDF
[DL輪読会]Understanding Black-box Predictions via Influence Functions PDF
PDF
PPTX
[研究室論文紹介用スライド] Adversarial Contrastive Estimation PDF
ゼロから始める深層強化学習(NLP2018講演資料)/ Introduction of Deep Reinforcement Learning Similar to 【解説】 一般逆行列
PDF
PPTX
PDF
PDF
PPTX
PDF
PDF
PDF
PDF
El text.tokuron a(2019).yamamoto190620 PDF
PDF
PDF
PDF
AI2: Safety and Robustness Certification of Neural Networks with Abstract Int... PDF
PPTX
PPTX
AI course report part 1(Fix) PDF
PDF
PDF
2022年度秋学期 応用数学(解析) 第7回 2階線形微分方程式(1) (2022. 11. 10) PDF
kosenconf_Tsukuba_sciences_slide 【解説】 一般逆行列
- 1.
- 2.
連立一次方程式・線形方程式を思い出す
• 中学では連立一次方程式
• (未知数の数)=(方程式の数)
•解は必ず一意に定まった
• 高校では線形方程式
• 線形方程式 Ax=b で表現
• 逆行列で解く: x=A-1b
• Aは正方and正則
• 大学以降は「解けない場合」を主に扱う
• (未知数の数)≠(方程式の数)
• Aが非正方or非正則
• 逆行列が定義されない!
2017/9/12【解説】 一般逆行列
2
−𝑥 + 2𝑦 = 0
𝑥 + 𝑦 = 3
∴
𝑥 = 2
𝑦 = 1
−1 2
1 1
𝑥
𝑦 =
0
3
∴
𝑥
𝑦 =
2
1
−1 2
1 1
0 1
𝑥
𝑦 =
0
3
2
∴
𝑥
𝑦 = ?
?
- 3.
- 4.
その最も素朴な対処法が一般逆行列
• 一般逆行列(一般化逆行列、擬似逆行列 etc.)
•逆行列を非正方・非正則行列へと拡張したモノ
• ある適当な尺度を導入して「解けない場合」に対処
• 通常は『Moore-Penrose一般逆行列』を指す(後述)
• 線形方程式 Ax=b を x=A-b のように解きたい
• 特にAが非正方・非正則な場合にも対応したい
• このA-を「Aの一般逆行列」と呼ぶ
2017/9/12【解説】 一般逆行列
4
𝑨𝒙 = 𝒃
𝒙 = 𝑨−
𝒃 𝑨 ∈ ℝ 𝑚×𝑛, 𝒃 ∈ ℝ 𝑚×1, 𝒙 ∈ ℝ 𝑛×1
m:方程式の数、n:未知数の数
では「解けない場合」をパターン分けして分析しよう
- 5.
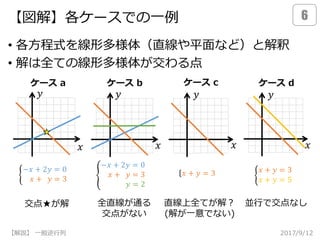
線形方程式を4ケースに分類して考える
a. Aが正方でフルランク: rank(A)=m=n
•逆行列A-1によって解が一意に定まる(決定系)
b. Aが縦長で列フルランク: rank(A)=n<m
• 全ての方程式を満足できる解がない(優決定系・不能)
c. Aが横長で行フルランク: rank(A)=m<n
• 方程式が足らず解が一意に定まらない(劣決定系・不定)
d. Aがランク落ち: rank(A)<min(m,n)
• 方程式に重複あり。重複除けば a,b,c のどれかに帰着
2017/9/12【解説】 一般逆行列
5
𝑨𝒙 = 𝒃 𝑨 ∈ ℝ 𝑚×𝑛
, 𝒃 ∈ ℝ 𝑚×1
, 𝒙 ∈ ℝ 𝑛×1
m:方程式の数、n:未知数の数
- 6.
- 7.
一般逆行列での各ケースに対する方針
a. そのまま逆行列として解く
b. 全ての方程式を満足できる解がない
•全方程式の二乗誤差を最小にする点を解として採用
• 単なる最小二乗法(正規方程式)として解ける
c. 方程式が足らず解が一意に定まらない
• 全解候補のうちベクトル長最小の点を解として採用
• Lagrangeの未定乗数法で解ける
d. ランク落ち
• 二乗誤差最小点のうちベクトル長最小点を解として採用
• 階数分解によってフルランク行列の積に分解して解く
• 結果としてbとcを順に適用した形に帰着
2017/9/12【解説】 一般逆行列
7
- 8.
b. 全方程式を満足する解がない:n<m
• 全方程式の二乗誤差が最小の点を解とする
•(目的関数の偏導関数)=0 をxについて解く
2017/9/12【解説】 一般逆行列
8
𝒙⋆ = arg min
𝒙
1
2
𝑨𝒙 − 𝒃 2
2
𝑓 𝒙 =
1
2
𝑨𝒙 − 𝒃 2
2
∈ ℝ
𝜕𝑓(𝒙)
𝜕𝒙
= 𝑨⊤
𝑨𝒙 − 𝒃 = 𝟎 ∈ ℝ 𝑛×1
𝑨⊤
𝑨𝒙 = 𝑨⊤
𝒃
∴ 𝒙⋆ = 𝑨⊤
𝑨 −1
𝑨⊤
𝒃
目的関数:二次関数 (微分可&凸)
制約集合:制約なし (Rnの全て)
↑いわゆる最小二乗法そのもの。
𝑨 ∈ ℝ 𝑚×𝑛
, 𝒃 ∈ ℝ 𝑚×1
, 𝒙 ∈ ℝ 𝑛×1
Aは列フルランク ⇒ ATAは正則
この式は通常『正規方程式』と呼ばれる
- 9.
c. 解が一意に定まらない:m<n
• 全解候補のうちL2ノルムが最小の点を解とする
•Lagrangeの未定乗数法で解く
• (Lagrange関数の偏導関数)=0 をxについて解く
2017/9/12【解説】 一般逆行列
9
𝒙⋆ = arg min
𝒙
1
2
𝒙 2
2
s. t. 𝑨𝒙 = 𝒃
ℒ 𝒙, 𝝀 =
1
2
𝒙⊤ 𝒙 − 𝝀⊤ 𝑨𝒙 − 𝒃 ∈ ℝ
𝜕ℒ 𝒙,𝝀
𝜕𝐱
= 𝒙 − 𝑨⊤
𝝀 = 𝟎 ∈ ℝ 𝑛
𝜕ℒ 𝒙,𝝀
𝜕𝛌
= −𝑨𝒙 + 𝒃 = 𝟎 ∈ ℝ 𝑚
目的関数:二次関数 (微分可&凸)
制約集合:線形等式制約
(かつ、Aは行フルランク)
𝑨 ∈ ℝ 𝑚×𝑛, 𝒃, 𝝀 ∈ ℝ 𝑚×1, 𝒙 ∈ ℝ 𝑛×1
Aは行フルランク
⇒ AATは正則
∴
𝒙⋆
𝝀
=
𝑨⊤ 𝑨𝑨⊤ −1 𝒃
𝑨𝑨⊤ −1 𝒃
- 10.
d. ランク落ち:rank(A)<min(m,n)
• 多数ある最小二乗点のうち最小ノルム点を解とする
•まずケースbして、その解候補の中からケースcする
• ランク落ちだと(ATA)-1や(AAT)-1が計算不可
• この難しさを階数分解 A=BC を使って回避
• 列フルランクなBおよび行フルランクなCの積に分解
• rank(A)=rとおくと、
• 「任意の行列は階数分解できる」[Wikipedia(汗]
• B,Cはフルランク→ケースb,cの結果を順に適用可
2017/9/12【解説】 一般逆行列
10
𝑨𝒙 = 𝑩𝑪𝒙 = 𝒃
𝒙 = 𝑨− 𝒃 = 𝑪− 𝑩− 𝒃 = 𝑪⊤ 𝑪𝑪⊤ −1 𝑩⊤ 𝑩 −1 𝑩⊤ 𝒃
𝑨 ∈ ℝ 𝑚×𝑛, 𝑩 ∈ ℝ 𝑚×𝑟, 𝑪 ∈ ℝ 𝑟×𝑛
Cは行フルランク ⇒ CCTは正則 Bは列フルランク ⇒ BTBは正則
- 11.
- 12.
全ケースでの結果をまとめると…
• A=BCを階数分解とすると、その一般逆行列は
• 特にAが正方・フルランクならばA-=A-1(ケースa)
• 特にAが列フルランクならば C=I(ケースb)
• 特にAが行フルランクならば B=I(ケースc)
• とりま階数分解で全ケースを包括的に捉えれたが…
• 階数分解のくだりが抽象的だしイメージしづらい?
• そこでより具体的な特異値分解の視点から捉えよう
• 特異値分解から階数分解の一例が容易に示せる
• 実用上は特異値分解の形こそが通常広く使われている
2017/9/12【解説】 一般逆行列
12
𝑨−
= 𝑪⊤
𝑪𝑪⊤ −1
𝑩⊤
𝑩 −1
𝑩⊤
- 13.
特異値分解は階数分解の代表的な例
• 行列A (m×nサイズ、r=rank(A))を特異値分解
• Aを直交行列U,Vと対角行列Σに分解
• 次のように変形すると階数分解に帰着
• Σとの乗算の結果残るのは、Uの左側とVTの上側のみ
2017/9/12【解説】 一般逆行列
13
𝑨 = 𝑼𝜮𝑽⊤
𝜮 =
𝜮 𝑟 𝟎
𝟎 𝟎
𝜮 𝑟 = diag 𝜎1, 𝜎2, … , 𝜎𝑟
𝑨 ∈ ℝ 𝑚×𝑛
, 𝑼 ∈ ℝ 𝑚×𝑚
, 𝜮 ∈ ℝ 𝑚×𝑛
, 𝑽 ∈ ℝ 𝑛×𝑛
, 𝜮 𝑟 ∈ ℝ 𝑟×𝑟
𝑨 = 𝑼𝜮𝑽⊤
= 𝑼 𝑟 𝑼 𝑚−𝑟
𝜮 𝑟 𝟎
𝟎 𝟎
𝑽 𝑟
⊤
𝑽 𝑛−𝑟
⊤ = 𝑼 𝑟 𝜮 𝑟 𝑽 𝑟
⊤
= 𝑼 𝑟 𝜮 𝑟 𝑽 𝑟
⊤ = 𝑼 𝑟 𝜮 𝑟 𝑽 𝑟
⊤ = 𝑩𝑪
- 14.
【図解】行列 (3×4、r=2) の特異値分解
2017/9/12【解説】一般逆行列
14
a11 a12 a13 a14
a21 a22 a23 a24
a31 a32 a33 a34
𝒖1 𝒖2 𝒖3
𝒗1
⊤
𝒗2
⊤
𝒗 𝟑
⊤
𝒗4
⊤
𝜎1 0
O
0 𝜎2
O O
𝑨 = 𝑼 𝜮 𝑽⊤
𝒖1 𝒖2
𝒗1
⊤
𝒗2
⊤
𝜎1 0
0 𝜎2
= 𝑼 𝑟 𝜮 𝑟 𝑽 𝑟
⊤
𝒖1 𝒖2
𝜎1 𝒗1
⊤
𝜎2 𝒗2
⊤
= 𝑼 𝑟 𝜮 𝑟 𝑽 𝑟
⊤
r=2なので、まさに階数分解の形!
(もちろんΣrをUr側に吸収させてもOK)
- 15.
一般逆行列を特異値分解で表現する
• んで導出したA-に を代入すると
•つまり、Aの一般逆行列A-の特異値分解は
• AT=VΣUTにおいて、その非ゼロ特異値を逆数にしたもの
• この特異値分解の表現はあらゆる場面で登場
• 学生レベルだとここまで理解しておけば大抵OK!
2017/9/12【解説】 一般逆行列
15
𝑨− = 𝑪⊤ 𝑪𝑪⊤ −1 𝑩⊤ 𝑩 −1 𝑩⊤
= 𝑽 𝑟 𝜮 𝑟 𝜮 𝑟 𝑽 𝑟
⊤ 𝑽 𝑟 𝜮 𝑟
−1 𝑼 𝑟
⊤ 𝑼 𝑟
−1 𝑼 𝑟
⊤ = 𝑽 𝑟 𝜮 𝑟
−1 𝑼 𝑟
⊤
𝑩 = 𝑼 𝑟, 𝑪 = 𝜮 𝑟 𝑽 𝑟
⊤
𝜮− = 𝜮 𝑟
−1
𝟎
𝟎 𝟎
∈ ℝ 𝑛×𝑚𝑨− = 𝑽𝜮− 𝑼⊤
- 16.
• 行列A (m×n=3×4,r=2)の特異値分解
• Aを直交行列U,Vと対角行列Σに分解
• その一般逆行列A-の特異値分解
• AT=VΣUTにおいて、その非ゼロ特異値を逆数にしたもの
𝜎1
−1
0
0 𝜎2
−1
𝜎1 0
0 𝜎2
【図解】一般逆行列と特異値分解の関係性
2017/9/12【解説】 一般逆行列
16
𝑨 = 𝑼 𝜮 𝑽⊤
𝑨−
= 𝑽 𝜮−
𝑼⊤
- 17.
Moore-Penrose一般逆行列 (MP逆)
2017/9/12【解説】 一般逆行列
17
(1).𝑨𝑨+ 𝑨 = 𝑨
(3). 𝑨+ 𝑨 ⊤ = 𝑨+ 𝑨
定義: Moore-Penrose一般逆行列
ある行列Aについて次の4条件を満たすA+のこと
• 巷で一般逆行列というとMP逆を指すことがほとんど
• 専門的な資料では以下のように呼び分けている
• 一般逆行列 A-: (1)を満たす(←複数ありうる)
• MP逆 A+: (1)~(4)の全てを満たす(←一意に決まる)
• 証明》MP逆の一意性
• Aに2つのMP逆X,Yがあると仮定し、X=Yを示す
(2). 𝑨+ 𝑨𝑨+ = 𝑨+
(4). 𝑨𝑨+ ⊤ = 𝑨𝑨+
𝑿 = 𝑿𝑨𝑿 = 𝑿 𝑨𝑿 ⊤ = 𝑿 𝑨𝒀𝑨𝑿 ⊤ = 𝑿 𝑨𝑿 ⊤ 𝑨𝒀 ⊤ = 𝑿𝑨𝑿𝑨𝒀 = 𝑿𝑨𝒀,
𝒀 = 𝒀𝑨𝒀 = 𝒀𝑨 ⊤ 𝒀 = 𝒀𝑨𝑿𝑨 ⊤ 𝒀 = 𝑿𝑨 ⊤ 𝒀𝑨 ⊤ 𝒀 = 𝑿𝑨𝒀𝑨𝒀 = 𝑿𝑨𝒀
- 18.
実は階数分解で導いた式はMP逆でした
• 証明》以下のように4条件全てを満たす
2017/9/12【解説】 一般逆行列
18
1.𝑨𝑨+
𝑨 = 𝑩𝑪 𝑪⊤
𝑪𝑪⊤ −1
𝑩⊤
𝑩 −1
𝑩⊤
𝑩𝑪 = 𝑩𝑪 = 𝑨
3. 𝑨+ 𝑨 = 𝑪⊤ 𝑪𝑪⊤ −1 𝑩⊤ 𝑩 −1 𝑩⊤ 𝑩𝑪
= 𝑪⊤ 𝑪𝑪⊤ −1 𝑪 = 𝑪⊤ 𝑪𝑪⊤ −1 𝑪 ⊤ = 𝑨+ 𝑨 ⊤
4. 𝑨𝑨+
= 𝑩𝑪 𝑪⊤
𝑪𝑪⊤ −1
𝑩⊤
𝑩 −1
𝑩⊤
= 𝑩 𝑩⊤ 𝑩 −1 𝑩⊤ = 𝑩 𝑩⊤ 𝑩 −1 𝑩⊤ ⊤ = 𝑨𝑨+ ⊤
2. 𝑨+
𝑨𝑨+
= 𝑪⊤
𝑪𝑪⊤ −1
𝑩⊤
𝑩 −1
𝑩⊤
𝑩𝑪 𝑪⊤
𝑪𝑪⊤ −1
𝑩⊤
𝑩 −1
𝑩⊤
= 𝑪⊤
𝑪𝑪⊤ −1
𝑩⊤
𝑩 −1
𝑩⊤
= 𝑨+
𝑨+ = 𝑪⊤ 𝑪𝑪⊤ −1 𝑩⊤ 𝑩 −1 𝑩⊤
定理:
A=BCを階数分解とすると、そのMP逆は
- 19.
当然、その特異値分解版もMP逆です
• 証明》以下のように4条件全てを満たす
2017/9/12【解説】 一般逆行列
19
𝑨+
=𝑽𝜮+
𝑼⊤
1. 𝑨𝑨+
𝑨 = 𝑼𝜮𝑽⊤
𝑽𝜮+
𝑼⊤
𝑼𝜮𝑽⊤
= 𝑼𝜮𝜮+
𝜮𝑽⊤
= 𝑨
3. 𝑨+ 𝑨 = 𝑽𝜮+ 𝑼⊤ 𝑼𝜮𝑽⊤ = 𝑽𝜮+ 𝜮𝑽⊤,
𝑨+
𝑨 ⊤
= 𝑽𝜮+
𝜮𝑽⊤ ⊤
= 𝑽 𝜮+
𝜮 ⊤
𝑽⊤
= 𝑽𝜮+
𝜮𝑽⊤
4. 𝑨𝑨+
= 𝑼𝜮𝑽⊤
𝑽𝜮+
𝑼⊤
= 𝑼𝜮𝜮+
𝑼⊤
,
𝑨𝑨+ ⊤
= 𝑼𝜮𝜮+
𝑼⊤ ⊤
= 𝑼 𝜮𝜮+ ⊤
𝑼⊤
= 𝑼𝜮𝜮+
𝑼⊤
2. 𝑨+ 𝑨𝑨+ = 𝑽𝜮+ 𝑼⊤ 𝑼𝜮𝑽⊤ 𝑽𝜮+ 𝑼⊤ = 𝑽𝜮+ 𝜮𝜮+ 𝑼⊤ = 𝑨+
定理:
A=UΣVTを特異値分解とすると、そのMP逆は
- 20.
MP逆の各条件の意味(詳細は次頁以降)
1. 𝑨𝑨+ 𝑨= 𝑨 (一般逆行列の必要十分条件)
• 要するに逆行列の条件 𝑨𝑨−1
= 𝑨−1
𝑨 = 𝑰 の一般化
2. 𝑨+ 𝑨𝑨+ = 𝑨+ (反射型一般逆行列)
• AとA+が対称性をもつようになる (rank A=rank A+)
3. 𝑨+ 𝑨 ⊤ = 𝑨+ 𝑨(最小ノルム型一般逆行列)
• Aの零空間(ker A)の補空間として直交補空間を採用
4. 𝑨𝑨+ ⊤ = 𝑨𝑨+(最小二乗型一般逆行列)
• Aの像(Im A)の補空間として直交補空間を採用
• この4条件を満たす一般逆は一意←これがMP逆
• 各条件の意味は写像・射影から説明できる(次頁)
2017/9/12【解説】 一般逆行列
20
- 21.
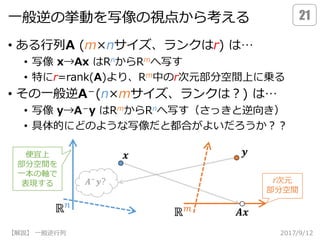
一般逆の挙動を写像の視点から考える
• ある行列A (m×nサイズ、ランクはr)は…
• 写像 x→Ax はRnからRmへ写す
• 特にr=rank(A)より、Rm中のr次元部分空間上に乗る
• その一般逆A-(n×mサイズ、ランクは?) は…
• 写像 y→A-y はRmからRnへ写す(さっきと逆向き)
• 具体的にどのような写像だと都合がよいだろうか??
2017/9/12【解説】 一般逆行列
21
ℝ 𝑛
ℝ 𝑚
𝒙
𝑨𝒙
𝒚
𝑨− 𝒚? r次元
部分空間
便宜上
部分空間を
一本の軸で
表現する
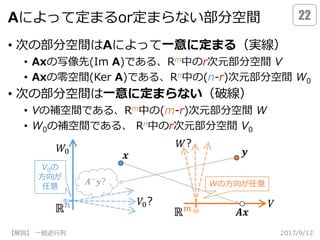
- 22.
- 23.
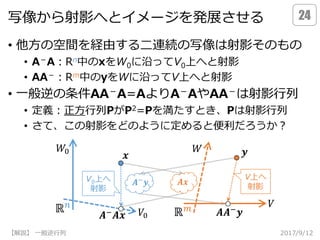
- 24.
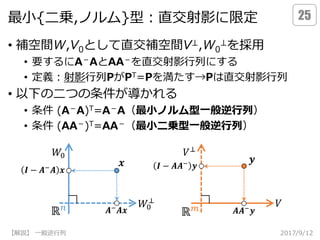
- 25.
- 26.
- 27.
- 28.
参考文献
1. 柳井晴夫, 竹内啓:“射影行列・一般逆行列・特異値分解”,
東京大学出版会, (1983).
2. 田辺国士: “一般逆行列 (1)”, 日本オペレーションズ・リ
サーチ学会, pp. 213-215, (1976/4).
3. 田辺国士: “一般逆行列 (2)”, 日本オペレーションズ・リ
サーチ学会, pp. 275-277, (1976/5).
4. 田辺国士: “一般逆行列 (3)”, 日本オペレーションズ・リ
サーチ学会, pp. 324-326, (1976/6).
5. “確率・統計 (24) 主成分回帰と部分最小二乗法”,
http://fussy.web.fc2.com/algo/stat24_pls.htm
2017/9/12【解説】 一般逆行列
28








![d. ランク落ち:rank(A)<min(m,n)
• 多数ある最小二乗点のうち最小ノルム点を解とする
• まずケースbして、その解候補の中からケースcする
• ランク落ちだと(ATA)-1や(AAT)-1が計算不可
• この難しさを階数分解 A=BC を使って回避
• 列フルランクなBおよび行フルランクなCの積に分解
• rank(A)=rとおくと、
• 「任意の行列は階数分解できる」[Wikipedia(汗]
• B,Cはフルランク→ケースb,cの結果を順に適用可
2017/9/12【解説】 一般逆行列
10
𝑨𝒙 = 𝑩𝑪𝒙 = 𝒃
𝒙 = 𝑨− 𝒃 = 𝑪− 𝑩− 𝒃 = 𝑪⊤ 𝑪𝑪⊤ −1 𝑩⊤ 𝑩 −1 𝑩⊤ 𝒃
𝑨 ∈ ℝ 𝑚×𝑛, 𝑩 ∈ ℝ 𝑚×𝑟, 𝑪 ∈ ℝ 𝑟×𝑛
Cは行フルランク ⇒ CCTは正則 Bは列フルランク ⇒ BTBは正則](https://image.slidesharecdn.com/random-170911062755/85/slide-10-320.jpg)