Downloaded 10 times
![ 特徴
非分離性、対称性、重複性を有する冗長変換
事例に基づく設計（辞書学習）が可能
非分離冗長重複変換(NSOLT)
2015/11/4 第30回信号処理シンポジウム 4
事例画像
学習辞書（要素画像群） [Muramatsu,ICASSP2014]
𝐃](https://image.slidesharecdn.com/random-151109010544-lva1-app6892/85/slide-4-320.jpg)
![スパース表現による画像復元
2015/11/4 第30回信号処理シンポジウム 5
原画像
PSNR→
観測画像
23.84 [dB]
復元画像
ウィーナー
21.99 [dB]
ISTA + →
PSNR →
冗長度 →
復元画像
非間引HT
27.17 [dB]
ℛ = 4
復元画像
NSOLT
27.27 [dB]
ℛ < 2.34](https://image.slidesharecdn.com/random-151109010544-lva1-app6892/85/slide-5-320.jpg)
![解析的勾配の速度評価
数値的勾配（有限差分）と解析的勾配の比較
２次元，4 × 4間引き，次数 2，2 𝑇
，直流無漏洩，𝑆 = 1, 𝑁 = 32 × 32
準ニュートン法（MATLAB R2015b fminunc, 反復数：20回）
2015/11/4 第30回信号処理シンポジウム 11
帯域数
𝑝𝑠 + 𝑝 𝑎
所要時間[s] 速度
比率
最大
相対誤差
(DerivativeCheck)数値的 解析的
8+8 120.23 1.45 83.14 1.26 × 10−9
9+9 170.79 1.41 121.48 1.63 × 10−9
10+10 228.26 1.69 134.93 1.11 × 10−9
11+11 282.40 1.85 152.80 1.92 × 10−9
12+12 342.52 1.92 178.60 1.02 × 10−9
CPU: Intel Core i7-3667U 2.00GHz, RAM:8GB, OS: Win8.1Pro(64)](https://image.slidesharecdn.com/random-151109010544-lva1-app6892/85/slide-11-320.jpg)
![ 要素画像（インパルス応答）群（𝑃 = 𝑝s + 𝑝a = 12 + 12）
事例：barbaraからの32 × 32画素パッチ（ランダム抽出𝑆 = 64）
スパース符号化実験の結果（PSNR[dB]）
実験緒言(𝑁 = 512 × 512, 𝐾 = 32,768, 𝐾/𝑁 = 0.125)
確率的勾配降下法による設計
2015/11/4 第30回信号処理シンポジウム 13
辞書 goldhill lena barbara baboon
Sparse K-SVD 33.55 34.87 29.35 26.22
SGD-NSOLT（提案法） 33.56 37.40 32.67 25.94](https://image.slidesharecdn.com/random-151109010544-lva1-app6892/85/slide-13-320.jpg)
非分離冗長重複変換の事例学習設計における効果的辞書更新
- 1.
- 2. 発表内容 研究背景と目的 NSOLTの構成と設計 目的関数の勾配導出 解析的勾配の効果的計算法の提案 確率的勾配降下（ＳＧＤ）法の導入 NSOLT設計の評価 まとめ 2015/11/4 第30回信号処理シンポジウム 2
- 3. 研究背景 冗長変換の応用例：画像復元 2015/11/4 第30回信号処理シンポジウム3 𝐛 観測 画像 𝐱 未知の 原画像 観測過程 𝐃 𝐲 𝐃 𝐲 冗長変換（辞書） スパース表現 𝐱 復元 画像 復元 冗長変換𝐃の選択は復元性能に影響大
- 4. 特徴 非分離性、対称性、重複性を有する冗長変換 事例に基づく設計（辞書学習）が可能 非分離冗長重複変換(NSOLT) 2015/11/4 第30回信号処理シンポジウム 4 事例画像 学習辞書（要素画像群） [Muramatsu,ICASSP2014] 𝐃
- 5. スパース表現による画像復元 2015/11/4 第30回信号処理シンポジウム 5 原画像 PSNR→ 観測画像 23.84[dB] 復元画像 ウィーナー 21.99 [dB] ISTA + → PSNR → 冗長度 → 復元画像 非間引HT 27.17 [dB] ℛ = 4 復元画像 NSOLT 27.27 [dB] ℛ < 2.34
- 6. 問題と目的 従来の設計（辞書学習）法 遺伝的アルゴリズム(GA)＆準ニュートン法 無数の局所解をもつ非線形な目的関数に対応 問題点 パラメータ数が数百、数千 ➡ 設計困難 特に、準ニュートン法に時間を要する 目的関数の数値的勾配（有限差分）計算がボトルネックに 2015/11/4 第30回信号処理シンポジウム 6 【目的】 設計の効率化 解析的勾配を導出、確率的勾配降下法を導入
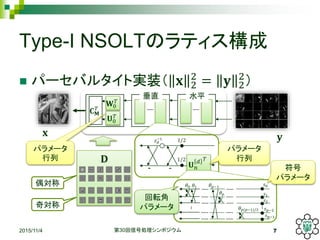
- 7. パーセバルタイト実装（ 𝐱2 2 = 𝐲 2 2 ） Type-I NSOLTのラティス構成 2015/11/4 第30回信号処理シンポジウム 7 𝐱 𝐲 垂直 水平 𝐂 𝐌 𝑇 𝐖0 𝑇 𝐔0 𝑇 𝐔 𝑛 𝑑 𝑇 - - 𝑧 𝑑 −1 1/2 1/2 パラメータ 行列 パラメータ 行列𝐃 𝜃0 𝜃1 𝜃 𝑝−1 𝜃 𝑝 𝜃 𝑝(𝑝−1)/2 𝑠0 𝑠1 𝑠2 𝑠 𝑝−2 𝑠 𝑝−1 符号 パラメータ 回転角 パラメータ 偶対称 奇対称
- 8. NSOLTの設計（辞書学習） 問題設定 𝐃, 𝐲𝑖= argmin 𝐃, 𝐲 𝑖 1 𝑆 𝑖=0 𝑆−1 𝐱 𝑖 − 𝐃𝐲𝑖 2 2 s. t. 𝐲𝑖 0 ≤ 𝐾 スパース符号化 𝐲𝑖 = argmin 𝐲 𝑖 𝐱 𝑖 − 𝐃𝐲𝑖 2 2 s. t. 𝐲𝑖 0 ≤ 𝐾, 𝑖 ∈ {0,1, ⋯ , 𝑆 − 1} 辞書更新 𝚯 = argmin 𝚯 1 𝑆 𝑖=0 𝑆−1 𝐱 𝑖 − 𝐃 𝚯 𝐲𝑖 2 2 𝐃 = 𝐃 𝚯 第30回信号処理シンポジウム 82015/11/4 スパース符号化 (変換係数 𝐲𝑖 の更新) 辞書更新 (パラメータ𝚯の更新) 収束判定 true false 事例画像群（事例数𝑆） 𝐱 𝑖 繰返しハード 閾値処理(IHT) 少ない係数で 良い近似を得たい GA ＋ 準ニュートン法 𝐲𝑖 𝐃 𝐃辞書更新が課題．特に， 有限差分による準ニュートン法 辞書 （要素画像群）
- 9. 辞書更新の目的関数 目的関数の勾配 ここで、 目的関数の勾配導出 2015/11/4第30回信号処理シンポジウム 9 𝑓 𝚯 = 1 𝑆 𝑖=0 𝑆−1 𝐫𝑖 𝚯 2 2 = 1 𝑆 𝑖=0 𝑆−1 𝐱 𝑖 − 𝐃 𝚯 𝐲𝑖 2 2 𝛻𝜽 𝑓 𝚯 = 𝜕 𝜕𝜃0 𝑓 𝚯 , 𝜕 𝜕𝜃1 𝑓 𝚯 , ⋯ , 𝜕 𝜕𝜃 𝐽−1 𝑓 𝚯 𝑇 , 𝐃 𝚯 𝐱 𝑖 𝐲𝑖 𝐱 𝑖 𝚯 誤差 𝐫𝑖 𝚯 𝜃0 𝜃1 𝜃 𝑝−1 𝜃 𝑝 𝜃 𝑝(𝑝−1)/2 𝜕 𝜕𝜃𝑗 𝑓 𝚯 = − 2 𝑆 𝑖=0 𝑆−1 𝐫𝑖 𝚯 , 𝜕 𝜕𝜃𝑗 𝐃 𝚯 𝐲𝑖 𝐆 𝚯 𝑗 = 𝜕 𝜕𝜃𝑗 𝐃 𝚯 𝐲𝑖 𝜕 𝜕𝜃𝑗 𝐃 𝚯 𝐲𝑖 偏微分システム 対象となる回転行列の 実装変更のみで良い 0 𝜃𝑗 + 𝜋/2 事例 近似 回転行列 の微分
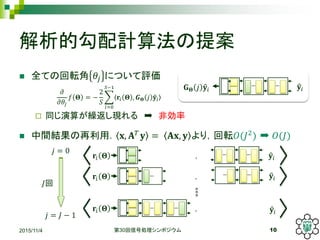
- 10. 解析的勾配計算法の提案 全ての回転角 𝜃𝑗について評価 同じ演算が繰返し現れる ➡ 非効率 中間結果の再利用． 𝐱, 𝐀 𝑇 𝐲 = 𝐀𝐱, 𝐲 より，回転𝑂(𝐽2 ) ➡ 𝑂(𝐽) 2015/11/4 第30回信号処理シンポジウム 10 𝜕 𝜕𝜃𝑗 𝑓 𝚯 = − 2 𝑆 𝑖=0 𝑆−1 𝐫𝑖 𝚯 , 𝑮 𝚯 𝑗 𝐲𝑖 𝐲𝑖𝐆 𝚯 𝑗 𝐲𝑖 ， 𝐫𝑖 𝚯 ， 𝐫𝑖 𝚯 ， 𝐫𝑖 𝚯 𝐲𝑖 𝐲𝑖 𝐲𝑖 𝑗 = 0 𝑗 = 𝐽 − 1 𝐽回
- 11. 解析的勾配の速度評価 数値的勾配（有限差分）と解析的勾配の比較 ２次元，4× 4間引き，次数 2，2 𝑇 ，直流無漏洩，𝑆 = 1, 𝑁 = 32 × 32 準ニュートン法（MATLAB R2015b fminunc, 反復数：20回） 2015/11/4 第30回信号処理シンポジウム 11 帯域数 𝑝𝑠 + 𝑝 𝑎 所要時間[s] 速度 比率 最大 相対誤差 (DerivativeCheck)数値的 解析的 8+8 120.23 1.45 83.14 1.26 × 10−9 9+9 170.79 1.41 121.48 1.63 × 10−9 10+10 228.26 1.69 134.93 1.11 × 10−9 11+11 282.40 1.85 152.80 1.92 × 10−9 12+12 342.52 1.92 178.60 1.02 × 10−9 CPU: Intel Core i7-3667U 2.00GHz, RAM:8GB, OS: Win8.1Pro(64)
- 12. 全ての事例 𝐱𝑖 について評価 事例をランダムに選択して評価 確率的勾配降下(SGD)法の導入 2015/11/4 第30回信号処理シンポジウム 12 𝛻𝜽 𝑓 𝚯 = 1 𝑆 𝑖=0 𝑆−1 𝛻𝜽 𝑓𝑖(𝚯) 𝛻𝛉 𝑓𝑖 𝚯 = 𝛻𝜽 𝐱 𝑖 − 𝐃 𝚯 𝐲𝑖 2 2 𝛻𝜽 𝑓 𝚯 ∼ 𝛻𝛉 𝑓𝑖 𝚯 事例毎の勾配 全事例の勾配（平均） 事例毎の勾配で近似 計算量削減 局所解脱出 𝜽 𝑘+1 = 𝜽 𝑘 − 𝜂 𝑘 𝛻𝜽 𝑓 𝚯 𝜽 𝑘+1 = 𝜽 𝑘 − 𝜂 𝑘 𝛻𝜽 𝑓𝑖 𝑘 𝚯
- 13. 要素画像（インパルス応答）群（𝑃 =𝑝s + 𝑝a = 12 + 12） 事例：barbaraからの32 × 32画素パッチ（ランダム抽出𝑆 = 64） スパース符号化実験の結果（PSNR[dB]） 実験緒言(𝑁 = 512 × 512, 𝐾 = 32,768, 𝐾/𝑁 = 0.125) 確率的勾配降下法による設計 2015/11/4 第30回信号処理シンポジウム 13 辞書 goldhill lena barbara baboon Sparse K-SVD 33.55 34.87 29.35 26.22 SGD-NSOLT（提案法） 33.56 37.40 32.67 25.94
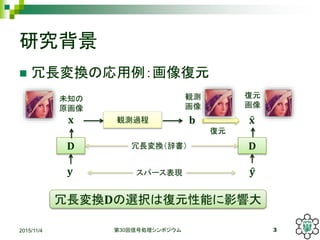
- 14. まとめ 辞書更新目的関数の解析的勾配を導出 偏微分合成システムを導出，効果的算出法を提案 数値的手法に比べ数十～数百倍の速度向上を確認 確率的勾配降下(SGD)法の導入 大規模な設計問題の最適化が可能に Sparse-KSVDと同等か優れた性能も得た 今後の課題 画像復元，特徴抽出等への応用 ボリュームデータへの適用 2015/11/4 第30回信号処理シンポジウム 14