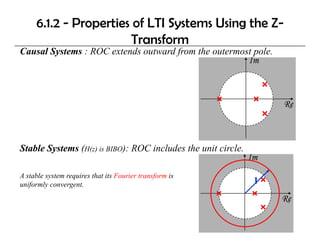
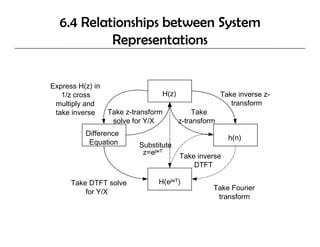
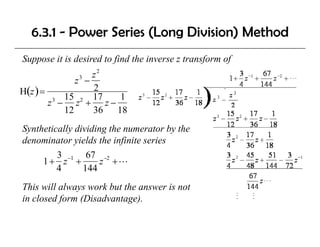
This document discusses the Z-transform and its application in digital signal processing. It covers topics such as: 1) Defining the Z-transform and how it can characterize linear time-invariant (LTI) systems. 2) Properties of LTI systems in the Z-domain, including causal and stable systems. 3) How the frequency response of a system can be obtained from its Z-transform. 4) Methods for finding the inverse Z-transform, including power series and partial fraction expansion. 5) Examples of using these techniques to analyze simple discrete systems.

1. EC533: Digital Signal Processing
5 l l
Lecture 6
The Z-Transform and its application in
signal processing

2. 6.1 - Z-Transform and LTI System
∞
• S t
System Function of LTI Systems:
F ti f LTI S t h (n ) = ∑ h (n )z − n
x(n )
n = −∞
h(n ) y (n )
Y (z )
X (z ) H (z ) Y (z ) H (z ) =
X (z )
• As the LTI system can be characterized by the difference equation, written as
• The diffe ence equation specifies the actual operation that must be performed by
he difference ope ation pe fo med
the discrete-time system on the input data, in the time domain, in order to generate
the desired output.
In Z domain
Z-domain
If the O/p of the system depends only on the present & past I/p samples but not
on previous outputs, i.e., bk=0’s FIR system, Else, Infinite Impulse Response
0s
(IIR)

3. 6.1.1 - LTI System Transfer Function
If the O/p of the system depends only on the present & past i/p samples but not
on previous outputs i.e., bk=0’s
outputs, i e 0s Finite Impulse Response (FIR) system ,
Finite Impulse Response (FIR) system
H (z ) = ∑ a k z − k
N
k =0 h(n) = 0, n < 0, h(n) = 0, n >N,
FIR system is an all zero system and are always stable
If bk≠0’s, the system is called Infinite Impulse Response (IIR) system
IIR filter has poles
h( n)
), -∞ ≤ n ≤ ∞

4. 6.1.2 - Properties of LTI Systems Using the Z-
Transform
Causal Systems : ROC extends outward from the outermost pole.
Im
R
Re
Stable Systems (H(z) is BIBO): ROC includes the unit circle.
Im
A stable system requires that its Fourier transform is
uniformly convergent. 1
Re

5. 6.2 - Z-transform and Frequency Response
Estimation
• The frequency response of a system (as digital filter spectrum) can be readily obtained
from its z-transform.
H(z)
H( )
as,
where σ is a transient term & it tends to zero as f
at steady state, Steady‐state frequency response of
a system (DTFT).
where, A(ω)≡ Amplitude (Magnitude) Response , B(ω) ≡ Angle (Phase) Response
Steady‐state

6. 6.2 - Frequency Response Estimation – cont.
• Phase Delay
The amount of time delay, each frequency component of the signal suffers in
delay
going through the system.
• Group Delay
The average time delay the composite signal suffers at each frequency.

7. 6.3 - Inverse Z-Transform
where
DTFT
IDTFT
(A contour integral)
where, for a fixed r,

8. 6.3 - The Inverse Z-Transform – cont.
• There is an inversion integral for the z transform,
1
x[n ] = X(z)z n−1dz
j2π ∫
C
but doing it requires integration in the complex plane and
it is rarely used in engineering practice.
• There are two other common methods,
Power series method (long division method)
Partial-Fraction Expansion
p

9. 6.3.1 - Power Series (Long Division) Method
Suppose it is desired to find the inverse z transform of
z2
z3 −
H(z ) = 2
15 2 17 1
z − z + z−
3
12 36 18
Synthetically dividing the numerator by the
denominator yields the infinite series
d i t i ld th i fi it i
3 −1 67 −2
1+ z + z +L
4 144
This will always work but the answer is not
in closed form (Disadvantage).

10. 6.3.2 - Partial-Fraction Expansion
•Put H(z-1) in a fractional form with the degree of numerator less than degree of
denominator.
•Put the denominator in the form of simple poles.
• A l partial fraction expansion.
Apply i lf i i
• Apply inverse z transform for those simple fractions.
Note
If N: order of numerator, & M: order of denominator.
then,
If N=M Divide
If 1N<M
If 1N<M Make direct P.F.
Make direct P F
If N>M Make long division then P.F.

11. Example 1:
find, a) Transfer Function b) Impulse Response
-1 -1/3 7/3
*3
3
3 3 3

12. Example 2:
Consider the discrete system,
a)
) Determine the poles & zeros.
D h l
b) Plot (locate) them on the z-plane.
c) Discuss the stability.
d) Find the impulse response.
e) Find the first 4 samples of h(n)
Solution:
a) zeros when N(z)=0 b)
z1=2 z2= - 0.5
poles when D(z)=0 xo x o
0.3 2
p1=0.3 p2= - 0.6
‐ 0.6 ‐ 0.5
c) Since all poles lies inside the unit circle, therefore the system is stable.

13. Example 2 – cont.
d) As discussed before, use partial fraction expansion and the table of transformation to
get the inverse z-transform
c) Divide N(z) by D(z) using long division,
) () y () g g ,
1
1 2 3
‐ 0.24
‐ 0.28
‐ 1.8

14. Example 3:
Consider the system described by the following difference equation,
Find,
a) The transfer function.
b) Th steady state frequency response.
The t d t t f
c) The O/p of the system when a sine wave of frequency 50 Hz & amplitude of 10 is
applied at its input, the sampling frequency is 1 KHz.
Solution:
a)

15. Example 3– cont.
b)

16. Example 3– cont.
c) x(n) = A sin(ω0 nT + θ )
1
= 10 sin((2π .50.n. ) + θ ) = 10 sin(0.1πn)
1000
Since the I/p is sinusoidal, the O/p should be sinusoidal,
y (n) = Ay sin(0.1πn + θ y )
where, A = A A(ω )
y x 0
θ y = θ x + θ (ω0 )
1
Ay = 10 ×
1 − (0.5 cos(ω0T )) 2 + (0.5 sin(ω0T )) 2
10
= = 18.3
1 − (0.5 cos(0.1π )) 2 + (0.5 sin(0.1π )) 2
⎛ 0.5 sin(0.1π ) ⎞
θ y = θ x − tan ⎜ −1
⎟ = 1780 24′
⎜ 1 − 0.5 cos(0.1π ) ⎟
⎝ ⎠

17. 6.4 Relationships between System
Representations
p
Express H(z) in
1/z cross H(z) Take inverse z-
multiply and transform
take inverse Take z-transform Take
solve for Y/X z-transform
Difference
h(n)
Equation Substitute
z=ejwT
Take inverse
DTFT
Take DTFT solve H(ejwT)
Take Fourier
for Y/X
transform