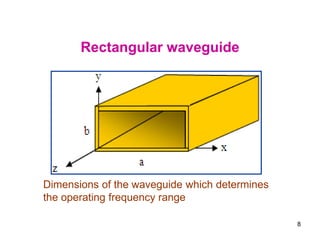
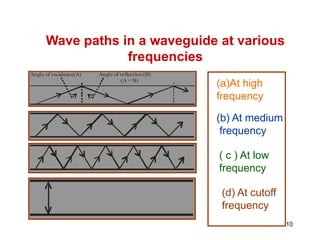
A waveguide is a structure that guides electromagnetic waves along its length. Rectangular waveguides consist of a hollow metal tube with a rectangular cross-section. Circular waveguides use a cylindrical cross-section. Waveguides can support transverse electric (TE) and transverse magnetic (TM) modes of propagation above a cutoff frequency that depends on the waveguide dimensions. Common applications include microwave communications, radar installations, and feeding antenna horns and dishes.

1. WAVE GUIDE
• A waveguide is an electromagnetic feed line used in microwave
communications, broadcasting, and radar installations. A
waveguide consists of a rectangular or cylindrical metal tube or
pipe. The electromagnetic field propagates lengthwise. Waveguides
are most often used with horn antenna s and dish antenna.
1

2. Introduction
At frequencies higher than 3 GHz, transmission of electromagnetic
energy along the transmission lines and cables becomes difficult.
This is due to the losses that occur both in the solid dielectric needed
to support the conductor and in the conductors themselves.
A metallic tube can be used to transmit electromagnetic wave at the
above frequencies
2

3. Waveguides
• Rectangular Waveguides
– TEM, TE and TM waves
– Cutoff Frequency
– Wave Propagation
– Wave Velocity,
3

4. 4
Possible Types of modes
1. Transverse Electro Magnetic (TEM) wave:
Here both electric and magnetic fields are directed
components. (i.e.) E z = 0 and Hz = 0
2. Transverse Electric (TE) wave: Here only the electric field is purely
transverse to the direction of propagation and the magnetic field is not purely
transverse. (i.e.) E z = 0, Hz ≠ 0

5. 5
4. Hybrid (HE) wave: Here neither electric nor
magnetic fields are purely transverse to the direction of propagation.
(i.e.) E z ≠ 0, Hz ≠ 0.
3. Transverse Magnetic (TM) wave: Here only magnetic field is transverse
to the direction of propagation and the electric field is not purely
transverse. (i.e.) E z ≠ 0, Hz = 0.
Possible Types of modes

6. 6

7. 7
Rectangular Waveguides
 Any shape of cross section of a waveguide
can support electromagnetic waves of
which rectangular and circular waveguides
have become more common.
 A waveguide having rectangular cross
section is known as Rectangular
waveguide

8. 8
Rectangular waveguide
Dimensions of the waveguide which determines
the operating frequency range

9. 9
1. The size of the waveguide determines its operating
frequency range.
2. The frequency of operation is determined by the
dimension ‘a’.
3. This dimension is usually made equal to one – half
the wavelength at the lowest frequency of operation,
this frequency is known as the waveguide cutoff
frequency.
4. At the cutoff frequency and below, the waveguide will
not transmit energy. At frequencies above the cutoff
frequency, the waveguide will propagate energy.
Dimensions of the waveguide which determines the
operating frequency range:

10. 10
Wave paths in a waveguide at various
frequencies
Angle of incidence(A) Angle of reflection (B)
(A = B)
(a)At high
frequency
(b) At medium
frequency
( c ) At low
frequency
(d) At cutoff
frequency

11. 11
Wave propagation
 When a probe launches energy into the
waveguide, the electromagnetic fields bounce
off the side walls of the waveguide as shown in
the above diagram.
 The angles of incidence and reflection depend
upon the operating frequency. At high
frequencies, the angles are large and therefore,
the path between the opposite walls is relatively
long as shown in Fig.

12. 12
At lower frequency, the angles decrease and the path between the sides
shortens.
When the operating frequency is reaches the cutoff frequency of the
waveguide, the signal simply bounces back and forth directly between the side
walls of the waveguide and has no forward motion.
At cut off frequency and below, no energy will propagate.

13. 13
Cut off frequency
 The exact size of the wave guide is selected
based on the desired operating frequency.
 The size of the waveguide is chosen so that
its rectangular width is greater than one –
half the wavelength but less than the one
wavelength at the operating frequency.
 This gives a cutoff frequency that is below
the operating frequency, thereby ensuring
that the signal will be propagated down the
line.

14. 14
Representation of modes
 The general symbol of representation will be TE m, n
or TM m, n where the subscript m indicates the
number of half wave variations of the electric field
intensity along the b ( wide) dimension of the
waveguide.
 The second subscript n indicates the number of half
wave variations of the electric field in the a (narrow)
dimension of the guide.
 The TE 1, 0 mode has the longest operating
wavelength and is designated as the dominant
mode. It is the mode for the lowest frequency that
can be propagated in a waveguide.

15. 15
Expression for cut off wavelength
 For a standard rectangular waveguide, the cutoff
wavelength is given by,

2
2
2














b
n
a
m
c

Where a and b are measured in centimeters

16. 16
A Hollow metallic tube of uniform
circular cross section for transmitting
electromagnetic waves by
successive reflections from the inner
walls of the tube is called Circular
waveguide.
Circular wave guide

17. 17
Circular wave guide
 The circular waveguide is used in many special
applications in microwave techniques.
 It has the advantage of greater power – handling
capacity and lower attenuation for a given cutoff
wavelength. However, the disadvantage of
somewhat greater size and weight.
 The polarization of the transmitted wave can be
altered due to the minor irregularities of the wall
surface of the circular guide, whereas the
rectangular wave guide the polarization is fixed

18. 18

19. 19
Description
 The wave of lowest frequency or the dominant
mode in the circular waveguide is the TE11 mode.
 The first subscript m indicates the number of full –
wave variations of the radial component of the
electric field around the circumference of the
waveguide.
 The second subscript n indicates the number of
half – wave variations across the diameter.
 The field configurations of TE11 mode in the
circular waveguide is shown in the diagram below

20. 20
Cut off wavelength
 The cutoff wavelength for dominant mode of
propagation TE11 in circular waveguide of radius
‘a’ is given by
1.814
π
2 a
c 

The cutoff wavelength for dominant mode of
propagation TM01 in circular waveguide of radius ‘a’
is given by
2.405
π
2 a
c 


21. 21
Applications of circular waveguide
 Rotating joints in radars to connect the horn
antenna feeding a parabolic reflector (which
must rotate for tracking)
 TE01 mode suitable for long distance waveguide
transmission above 10 GHz.
 Short and medium distance broad band
communication (could replace / share coaxial
and microwave links)

22. 22
Worked Example 2.4
 The dimensions of the waveguide are 2.5 cm  1 cm.
The frequency is 8.6 GHz. Find (i) possible modes
and (ii) cut – off frequency for TE waves.
Solution:
Given a = 2.5 cm , b = 1 cm and f = 8.6 GHz
Free space wavelength
cm
488
.
3
10
8
10
3
9
10
0 




f
C


23. 23
Solution
The condition for the wave to propagate is
that λC > λ0
For TE01 mode
cm
2
1
2
2
2
2
2
2
2
2
2






 b
a
ab
a
n
b
m
ab
C

Since λC < λ0, TE01 does not propagate

24. 24
 For TE10 mode, λC = 2a = 2  2.5 = 5 cm
 Since λC > λ0 , TE10 mode is a possible mode.
Cut – off frequency = GHz
6
5
10
3 10




C
C
C
f

Cut-off wavelength
for TE11 mode
cm
856
.
1
)
1
(
)
5
.
2
(
1
5
.
2
2
2
2





2
2
2
b
a
ab

For TE11 λC < λ0 , TE11 is not possible.
The possible mode is TE10 mode.
The cut – off frequency = 6 GHz
=

25. 25
Worked Example 2.5
 For the dominant mode propagated in an air filled
circular waveguide, the cut – off wavelength is 10 cm.
Find (i) the required size or cross sectional area of the
guide and (ii) the frequencies that can be used for this
mode of propagation
The cut – off wavelength = λC = 10 cm
The radius of the circular waveguide ,
cm
3
9
.
2
2
841
.
1
10



=
r

26. Waveguides
• In the previous chapters, a pair of
conductors was used to guide
electromagnetic wave propagation.
This propagation was via the
transverse electromagnetic (TEM)
mode, meaning both the electric and
magnetic field components were
transverse, or perpendicular, to the
direction of propagation.
• In this chapter we investigate wave-
guiding structures that support
propagation in non-TEM modes,
namely in the transverse electric (TE)
and transverse magnetic (TM) modes.
• In general, the term waveguide refers
to constructs that only support non-
TEM mode propagation. Such
constructs share an important trait:
they are unable to support wave
propagation below a certain frequency,
termed the cutoff frequency.
Rectangular
waveguide
Circular
waveguide
Optical Fiber
Dielectric Waveguide
26

27. Rectangular Waveguide
Location of modes
• Let us consider a rectangular waveguide
with interior dimensions are a x b,
• Waveguide can support TE and TM modes.
– In TE modes, the electric field is transverse
to the direction of propagation.
– In TM modes, the magnetic field that is
transverse and an electric field component is
in the propagation direction.
• The order of the mode refers to the field
configuration in the guide, and is given by m
and n integer subscripts, TEmn and TMmn.
– The m subscript corresponds to the number
of half-wave variations of the field in the x
direction, and
– The n subscript is the number of half-wave
variations in the y direction.
• A particular mode is only supported above
its cutoff frequency. The cutoff frequency is
given by
2 2 2 2
1
2 2
mn
r r
c
m n c m n
f
a b a b
  
  
       

       
       
Rectangular Waveguide
1 1 1 1
o r o r o o r r r r
c
u
          
    8
where 3 10 m/s
c   27

28. Table 7.1: Some Standard Rectangular Waveguide
Waveguide
Designation
a
(in)
b
(in)
t
(in)
fc10
(GHz)
freq range
(GHz)
WR975 9.750 4.875 .125 .605 .75 – 1.12
WR650 6.500 3.250 .080 .908 1.12 – 1.70
WR430 4.300 2.150 .080 1.375 1.70 – 2.60
WR284 2.84 1.34 .080 2.08 2.60 – 3.95
WR187 1.872 .872 .064 3.16 3.95 – 5.85
WR137 1.372 .622 .064 4.29 5.85 – 8.20
WR90 .900 .450 .050 6.56 8.2 – 12.4
WR62 .622 .311 .040 9.49 12.4 - 18
Location of modes
Rectangular Waveguide
Rectangular Waveguide
The cutoff frequency is given by
2 2
2
mn
r r
c
c m n
f
a b
 
 
   
   
   
2 2
2
mn
c
c m n
f
a b
 
   
   
   
8
where 3 10 m/s
c  
r
r
For air 1
and 1




28

29. To understand the concept of cutoff frequency, you can use the analogy of a road
system with lanes having different speed limits.
29

30. Rectangular Waveguide
Rectangular Waveguide
• Let us take a look at the field pattern for two
modes, TE10 and TE20
– In both cases, E only varies in the x direction;
since n = 0, it is constant in the y direction.
– For TE10, the electric field has a half sine
wave pattern, while for TE20 a full sine wave
pattern is observed.
30

31. Rectangular Waveguide
Example
Let us calculate the cutoff frequency for the first four modes of WR284 waveguide.
From Table 7.1 the guide dimensions are a = 2.840 mils and b = 1.340 mils.
Converting to metric units we have a = 7.214 cm and b = 3.404 cm.
2 2
2
mn
c
c m n
f
a b
 
   
   
   
 
8
10
3 10 100
2.08 GHz
2 2 7.214 1
c
m
x
c cm
s
f
a cm m
  
 
8
01
3 10 100
4.41 GHz
2 2 3.404 1
c
m
x
c cm
s
f
b cm m
  
20
4.16 GHz
c
c
f
a
 
8 2 2
11
3 10 1 1 100
4.87 GHz
2 7.214 3.404 1
c
m
x cm
s
f
cm cm m
  
   
   
   
TE10:
TE01:
8
where 3 10 m/s
c  
TE20:
TE11:
TE10 TE01
TE20 TE11
2.08 GHz 4.16 GHz 4.41 GHz 4.87 GHz
TM11
31

32. Rectangular Waveguide
Example
8
For air 3 10 m/s
c  
32

33. Rectangular Waveguide - Wave Propagation
We can achieve a qualitative understanding of
wave propagation in waveguide by considering the
wave to be a superposition of a pair of TEM waves.
Let us consider a TEM wave propagating in the z
direction. Figure shows the wave fronts; bold lines
indicating constant phase at the maximum value of
the field (+Eo), and lighter lines indicating constant
phase at the minimum value (-Eo).
The waves propagate at a velocity uu, where the u
subscript indicates media unbounded by guide
walls. In air, uu = c.
33

34. Now consider a pair of identical TEM waves, labeled
as u+ and u- in Figure (a). The u+ wave is
propagating at an angle + to the z axis, while the u-
wave propagates at an angle –.
These waves are combined in Figure (b). Notice that
horizontal lines can be drawn on the superposed
waves that correspond to zero field. Along these
lines the u+ wave is always 180 out of phase with
the u- wave.
Rectangular Waveguide - Wave Propagation
34

35. Rectangular Waveguide - Wave Propagation
Since we know E = 0 on a perfect conductor, we can replace
the horizontal lines of zero field with perfect conducting walls.
Now, u+ and u- are reflected off the walls as they propagate
along the guide.
The distance separating adjacent zero-field lines in Figure (b),
or separating the conducting walls in Figure (a), is given as the
dimension a in Figure (b).
The distance a is determined by the angle  and by the
distance between wavefront peaks, or the wavelength . For a
given wave velocity uu, the frequency is f = uu/.
If we fix the wall separation at a, and change the frequency, we
must then also change the angle  if we are to maintain a
propagating wave. Figure (b) shows wave fronts for the u+
wave.
The edge of a +Eo wave front (point A) will line up with the
edge of a –Eo front (point B), and the two fronts must be /2
apart for the m = 1 mode.
(a)
(b)
a
35

36. Rectangular Waveguide - Wave Propagation
The waveguide can support propagation as long as the wavelength
is smaller than a critical value, c, that occurs at  = 90, or
2 u
c
c
u
a
m f
  
Where fc is the cutoff frequency for the propagating mode.
sin c
c
f
f



 
We can relate the angle  to the operating frequency and
the cutoff frequency by
2
sin
m
a

 
For any value of m, we can write by simple trigonometry
2
sin u
u
a
m f
 
 
36

37. Rectangular Waveguide - Wave Propagation
A constant phase point moves along the wall from A to D. Calling
this phase velocity up, and given the distance lAD is
2
cos
AD
m
l



Then the time tAD to travel from A to D is
2
cos
AD
p p
AD
l m
t
u u


 
Since the times tAD and tAC must be equal, we have
cos
u
p
u
u


The time tAC it takes for the wavefront to move from A
to C (a distance lAC) is
2
Wavefront Velocity
Distance from A to C
AC
u u
AC
l m
t
u u

  
37

38.  
2
1
u
p
c
u
u
f
f


Rectangular Waveguide - Wave Propagation
 2
2 2
cos cos 1 sin 1 c
f f
  
    
cos
u
p
u
u


The Phase velocity is given by
using
cos
G u
u u 

 
2
1 c
G u
f
u u
f
 
The Group velocity is given by
The Wave velocity is given by
1 1 1 1
u
o r o r o o r r r r
c
u
          
   
8
where 3 10 m/s
c  
Wave velocity
Phase velocity
p
u
Group velocity
Beach
Ocean
Phase velocity
p
u
u
u
Wave velocity
u
u
G
u Group velocity
Analogy!
Point of contact
38

39. Rectangular Waveguide - Wave Propagation
The ratio of the transverse electric field to the transverse magnetic field for a
propagating mode at a particular frequency is the waveguide impedance.
2
,
1
TE u
mn
c
Z
f
f



 
 
 
For a TE mode, the wave impedance is For a TM mode, the wave impedance is
2
.
1
TM c
mn u
f
Z
f

 
   
 
 
2
1 c
u
f
f
 
 
The phase constant is given by
 
2
1
u
c
f
f

 

The guide wavelength is given by
39

40. Example
Rectangular Waveguide
40

41. Example
Rectangular Waveguide
Let’s determine the TE mode impedance looking into a 20 cm long section of shorted WR90
waveguide operating at 10 GHz.
From the Waveguide Table 7.1, a = 0.9 inch (or) 2.286 cm and b = 0.450 inch (or) 1.143 cm.
2 2
2
mn
c
c m n
f
a b
 
   
   
    TE10 6.56 GHz
Mode Cutoff Frequency
TE01 13.12 GHz
TE11 14.67 GHz
TE20 13.13 GHz
TE02 26.25 GHz
At 10 GHz, only the TE10 mode is supported!
TE10 6.56 GHz
Mode Cutoff Frequency
TE01 13.12 GHz
TE11 14.67 GHz
TE20 13.13 GHz
TE02 26.25 GHz
TE10 TE20
TE01 TE11
TM11
6.56 GHz 13.12 GHz
TE02
26.25 GHz
14.67 GHz
Rearrange
13.13 GHz
41

42. Example
Rectangular Waveguide
10
2
120
500 .
6.56GHz
1-
10GHz
TE
Z
 
  
 
 
 
 
10 tan
IN
TE
Z jZ 
 l
The impedance looking into a short circuit is
given by
The TE10 mode impedance
 
2 2
9 2
8
2
1 1
2 10 10 6.56
1 158
10
3 10
c c
u
f f
f
f c f
x Hz GHz rad
m GHz m
x
s

 

   
  
   
   
   
 
 
 
The TE10 mode propagation constant is
given by
   
500 tan 31.6 100
IN
Z j j
   
 
500 tan 158 0.2
IN
rad
Z j m
m
 
 

 
 
42