This document provides an outline for a thesis on analyzing transverse electric (TE) modes of rectangular hollow waveguides using the finite element method. It includes sections on reviewing different finite element approaches, introducing waveguides and electromagnetic field configurations within waveguides, developing the finite element formulation, providing an example analysis of a homogeneous hollow waveguide, comparing finite element results to analytical solutions, and plans for future work and references. The goal is to use the finite element method to calculate the propagation constant of TE modes in rectangular hollow waveguides and validate the approach against exact solutions.

1. by
Anuj
14/MAP/0012
M.Sc. (Applied Physics)
Under the guidance of
Dr. Manmohan Singh Shishodia
Gautam Buddha University, Greater Noida (U.P.)
Finite Element Method for Analyzing TE
Modes of Rectangular Hollow Waveguide

2. Outlines
 Review of Different Approaches Based On Finite Element
Method
 Introduction To Waveguide
 EM Field Configuration Within The Waveguide
 FEM Formulation
 Homogeneous Hollow waveguide Example
 MATLAB Code To Calculate Propagation Constant
 Result and comparison b/w FEM and Analytical Results
 Overall Summary
 Future Plan
 References

4. Review of Different Approaches Based On
Finite Element Method
FINITE ELEMENT METHOD: finite element method is a numerical technique to
solve the ordinary/partial differential equation.
1.Weighted Residual Method
Boundary value problem
i. Galerkin’s
ii. Least Square
iii. Collocation
‘types of element’
 
R
j
R
j njdguLd )1(1,0)(Re 
0Re2



 d
Ai
 
b
a
i nidxxx )1(1,0)(Re
SDgLu  ,
_
Re uL

5. 0.0 0.2 0.4 0.6 0.8 1.0
-0.008
-0.004
0.000
0.004
0.008
0.012
(yT/WL
2
)
x/L
Galerkin
Least Square
Collocation
ERROR PLOT FOR DIFFERENT APPROACHES
0.0 0.2 0.4 0.6 0.8 1.0
-0.30
-0.25
-0.20
-0.15
-0.10
-0.05
0.00
0.05
Solutions obtained from different methods
(yT/WL
2
)
x/L
Exact, Collocation
Galerkin, Least Square
Review of Different Approaches Based On
Finite Element Method
0)(2
2
 xw
dx
yd
T
032
2
 W
dx
yd
T
2
0
L
xfor 
02
2
W
dx
yd
T Lx
L
for 
2
* Hence the plot shown that the eroor is least in the Galerkin’s approach.

6. Introduction To Waveguide
 A Hollow metallic tube of uniform cross section for transmitting electromagnetic waves
by successive reflections from the inner walls of the tube is called waveguide.
 It may be used to carry energy over longer distances to carry transmitter power to an
antenna or microwave signals from an antenna to a receiver.
 Waveguides are made from copper, aluminum or brass. These metals are extruded into
long rectangular or circular pipes.
The electric and magnetic fields associated with the signal bounce off the inside walls
back and forth as it progresses down the waveguide.
*Fig. Three-dimensional view of the electric field for the TE₁₀– mode in a
rectangular waveguide
*http://www.radartutorial.eu/03.linetheory/Waveguides.en.html

7. EM Field Configuration Within The Waveguide
 In order to determine the EM field configuration within the waveguide, Maxwell’s
equations should be solved subject to appropriate boundary conditions at the walls of the
guide.
 Such solutions give rise to a number of field configurations. Each configuration is known
as a mode.
02
2
2
2
2






z
zz
Ek
y
E
x
E
022
 EkE
ck 22

)()(),( yYxXyxEz 
t
B
EE





,0
t
E
c
BB


 2
1
0
02
2
2
2
2
2





















zEk
cyx

     xkBxkAxX xx cossin 
02
2
2
2
2
2















 XYk
cdy
Yd
X
dx
Xd
Y

   bnaxmEEz /cos/cos0 
 





















22
22
/
b
n
a
m
ck 
mn
b
n
a
m
c  





















22
Scalar Wave Equation
Where
Maxwell’s Equations
*David J. Griffiths, “Introduction to Electrodynamics” Pearson Education, Inc., ISBN-978-81-203-1601-0 (1999),.

8. Possible Types of modes
Transverse Electromagnetic (TEM):
Here both electric and magnetic fields are directed
components. (i.e.) E z = 0 and Hz = 0
Transverse Electric (TE) wave:
Here only the electric field is purely transverse to the direction of propagation and
the magnetic field is not purely transverse. (i.e.) E z = 0, Hz ≠ 0.
Transverse Magnetic (TM) wave:
Here only magnetic field is transverse to the direction of propagation and the electric
field is not purely transverse. (i.e.) E z ≠ 0, Hz = 0.
Dimensions of the waveguide which determines the
operating frequency range
EM Field Configuration Within The Waveguide
    mnbnamc  
22
//
Where is the cutoff frequency

9.  The size of the waveguide determines its operating frequency range.
 The frequency of operation is determined by the dimension ‘a’ and b.
 This dimension is usually made equal to one – half the wavelength at the
lowest frequency of operation, this frequency is known as the waveguide cutoff
frequency.
 At the cutoff frequency and below, the waveguide will not transmit energy. At
frequencies above the cutoff frequency, the waveguide will propagate energy.
Angle of incidence(A) Angle of reflection (B)
(A = B)
(a)At high frequency
(b) At medium frequency
( c ) At low frequency
(d) At cutoff frequency
EM Field Configuration Within The Waveguide

10. 022
 k
dsk
yx
F
s
 























 22
22
2
1
)(
,
22
0
2
zr kkk  
0
0
2


k
  dSk
yx
F e
ee
N
e A
e
e
























 
22
22
2
1
 
2
22 ,
e
yx

 
3
33 ,
e
yx

 11
1
, yx
e
 yxP ,
x
y
Element e
1
2 3
cybxae 
FEM Formulation
 The scalar wave equation for a homogeneous isotropic medium is chosen.
 The scalar wave equation has many applications.
 It can be used to analyse problem such as the propagation of plane waves.
 It can be used to analyse the TE and TM modes in waveguides/weakly guiding optical
fibers.
The FEM solution of the above scalar equation by minimisation of a corresponding
functional is given by
The function at a point inside the triangle may be
approximated as , the linear terms:-
e
Fig. A typical first order triangular element.

11. 111 cybxae  222 cybxae  333 cybxae 
the solution of these equations gives
 

3
1
3
1
3
1 i
eii
i
eii
i
eii ccbbaa


































c
b
a
yx
yx
yx
e
e
e
1
1
1
33
22
11
3
2
1





































3
2
1
212113133232
123123
211332
2
1
e
e
e
xyyxxyyxxyyx
xxxxxx
yyyyyy
A
c
b
a











1
1
1
2
1
33
22
11
yx
yx
yx
A
FEM Formulation
where
……………………………………………..(1)

12.      23132132321
2
1
,
2
1
,
2
1
xx
A
cyy
A
bxyyx
A
a 
     31113213132
2
1
,
2
1
,
2
1
xx
A
cyy
A
bxyyx
A
a 
     12321321213
2
1
,
2
1
,
2
1
xx
A
cyy
A
bxyyx
A
a 
Hence, we can write
ei
i
ie u  
3
1
 321 eeee   321 uuuu   321 bbbb  321 cccc 
Using row vectors
 
   
 
dS
uukc
cbb
F
e
e
N
e A
t
e
tt
e
t
e
tt
e
t
e
tt
e
 










1 22
1
   

eN
e
t
eee
t
eee QkPF
1
2
2
1
FEM Formulation
   

eN
e
t
eee
t
eee QkPF
1
2
2
1  ccbbAP tt
ee 











211
121
112
12
e
e
A
Q
Using eqn (1)

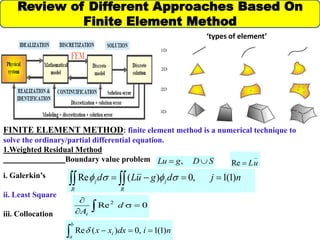
13. Homogeneous Hollow Waveguide Example
The example of a homogeneous hollow waveguide (WR-90) is taken to calculate the value of
propagation constant.[WR-90 waveguide :- frequency range:- 8.2GHz to 12.4GHz]
The dimensions of the waveguide is 2.286cm*1.016cm.
First we will dicretize the domain (waveguide) using “pde-toolbox” , this process is known as
meshing,.
Then we create three matrices....
1. For triangle node numbers:- A file element which has three node numbers of each triangle,
with rows arranged to correspond to triangle number in ascending order.
2. Coordinates of nodes:- A file coord which has two columns containing x coordinate in the
first column and y coordinate in the second, with rows arranged to correspond to node
numbers in ascending order.
3. Boundary node numbers:- A file bn with one column containing the boundary node numbers
in ascending order.

14. function [pe,qe] = triangle1(x,y)
ae=x(2)*y(3)-x(3)*y(2)+x(1)*y(2)-x(2)*y(1)-x(1)*y(3)+x(3)*y(1);
ae=abs(ae)/2;
b=[y(2)-y(3),y(3)-y(1),y(1)-y(2)];
c=[x(3)-x(2),x(1)-x(3),x(2)-x(1)];
b=b/(2*ae);
c=c/(2*ae);
pe=(b.'*b+c.'*c)*ae;
qe=[2,1,1;1,2,1;1,1,2];
qe=qe*(ae/12);
end
MATLAB Code To Calculate Propagation Constant
Function
clc
clear all
format long g
% load the data file
element=xlsread('element.xlsx');
coord=xlsread('coord.xlsx');
bn=xlsread('bn.xlsx');
% find the total no. of elements and nodes
ne=length(element(:,1));
nn=length(coord(:,1));
% set up pull global matrices
pg=zeros(nn,nn);
qg=zeros(nn,nn);
% sum over triangles
for e=1:ne;
% Get the three node no. of triangle no. e
node=[element(e,:)];
% Get the coordinates of each node and form row vectors
x=[coord(node(1),1),coord(node(2),1),coord(node(3),1)];
y=[coord(node(1),2),coord(node(2),2),coord(node(3),2)];
% Calculate the local matrix for triangle no. e
[pe,qe]=triangle1(x,y);
% Add each element of the local matrix to the appropriate lement
of the
% global matrix
for k=1:3;
for m=1:3;
pg(node(k),node(m))=pg(node(k),node(m))+pe(k,m);
qg(node(k),node(m))=qg(node(k),node(m))+qe(k,m);
end
end
end
ksquare=eig(pg,qg)
Script

15. Result and comparison b/w FEM and Analytical
Results
No mode 9.5748
(9.56119)
38.4625
(38.24479)
1.8891
(1.8886)
11.4693
(11.4498)
40.3694
(40.1334)
7.5638
(7.5545)
17.159
(17.1157)
46.11235
(45.7993)
m
n
0
0
1
1
2
2

16. Overall Summary
 Learned fundamentals of PDEs useful for scientists and engineers
(e.g., elliptic, parabolic & hyperbolic, scalar wave eqn).
 Studied waveguide and learned its different fundamental mode i.e.
TE.
Calculated values of propagation constant for different modes.

17. Future Plan
 In future, we will calculate the propagation constant for TM mode.
we will solve the problems on waveguide using ANSYS.
We will move towards optical wave guide and plasmonic waveguide
and study the different properties with the help of ANSYS .

18. 1. Erik G. Thompson, “An Introduction To The Finite Element Method”, John Willey &
Sons, ISBN: 978-81-265-2455-6 (2005)
2. Radhey S. Gupta, “Elements of Numerical Analysis”, Macmillan India Ltd.,ISBN: 446-
521 (2009),.
3. David J. Griffiths, “Introduction to Electrodynamics” Pearson Education, Inc., ISBN-
978-81-203-1601-0 (1999),.
References

19. Thank
You !!!