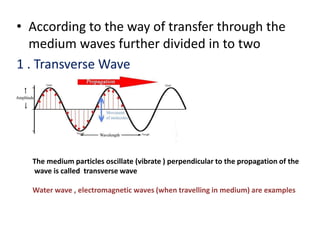
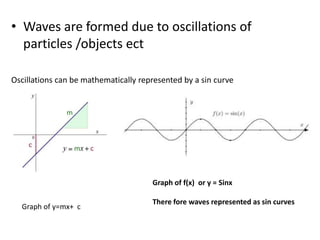
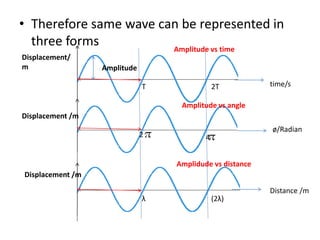
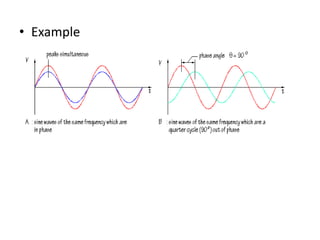
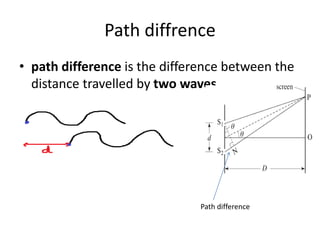
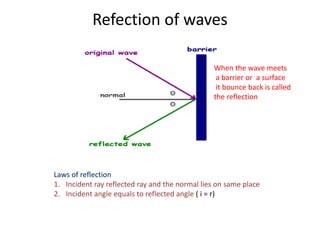
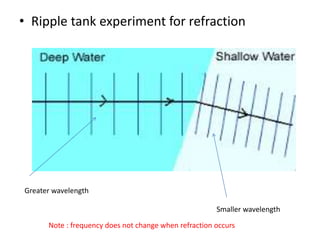
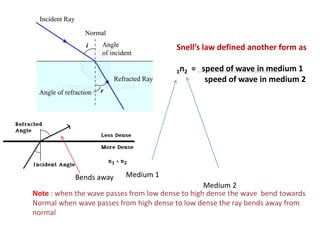
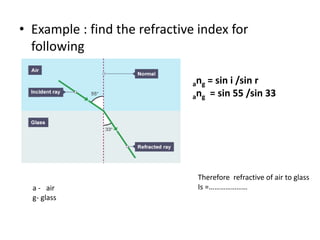
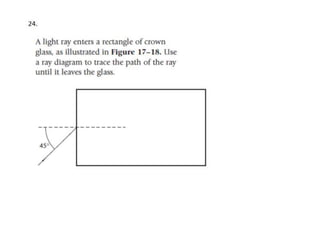
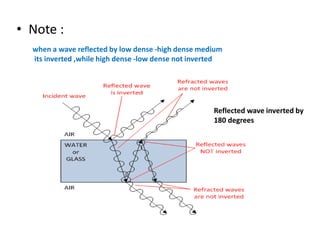
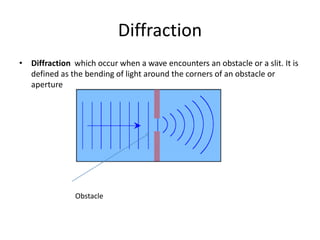
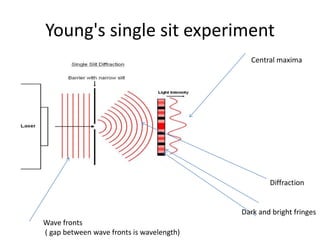
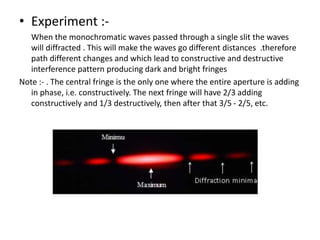
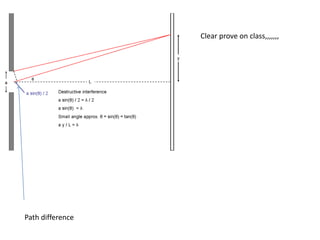
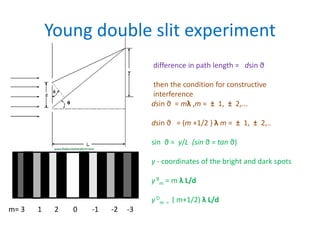
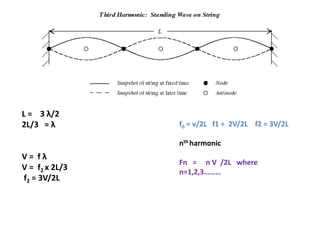
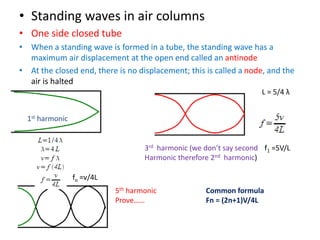
Waves can be categorized as mechanical or electromagnetic. Mechanical waves require a medium to travel through, while electromagnetic waves do not. Waves can also be transverse or longitudinal depending on the direction of particle oscillation relative to wave propagation. Important wave properties include amplitude, wavelength, frequency, and speed. Reflection, refraction, diffraction, interference, and polarization are key wave phenomena. Reflection follows the laws of reflection, while refraction follows Snell's law. Diffraction and interference result in constructive and destructive patterns. Polarization occurs when waves vibrate in a single plane. Waves have many applications including ultrasound imaging, fiber optics, and 3D displays.

1. Wave properties
Imath A.Latheef

2. Wave : wave is a form of energy
transfer
• Wave categorized in to two forms
1. Mechanical wave- need a medium to travel
Ex : Body waves
Water waves
Sound waves
2.Electromagnetic waves- no need a medium to travel
Ex:
X-ray
Radio waves
Visible region

3. • According to the way of transfer through the
medium waves further divided in to two
1 . Transverse Wave
The medium particles oscillate (vibrate ) perpendicular to the propagation of the
wave is called transverse wave
Water wave , electromagnetic waves (when travelling in medium) are examples

4. 2.Longitudinal waves
Medium particles oscillate in the direction of
wave propagation as Compression and
rare fractions
Sound wave is a good example for longitudinal wave

5. • Waves are formed due to oscillations of
particles /objects ect
Oscillations can be mathematically represented by a sin curve
Graph of y=mx+ c
Graph of f(x) or y = Sinx
There fore waves represented as sin curves

6. • Therefore same wave can be represented in
three forms
time/s
Distance /m
ø/Radian
Displacement/
m
Displacement /m
Displacement /m
T 2T
2 4
λ (2λ)
Amplitude vs time
Amplitude vs angle
Amplidude vs distance
Amplitude

7. • Definitions
Amplitude (A)
Maximum displacement of the medium particle from he
equilibrium position is called amplitude
Period (T)
The time for one complete oscillation called period
Frequency (f)
Number of oscillation in unit time (1sec) is called frequency
Wavelength
The distance between a wave with same phase is wavelength

8. Phase
• Phase is the points in the adjacent cycles of a
waveform (or the angles in a wave form is
phase )

9. Phase difference
When two waves represented the different in angle between the of two
waves is the phase difference

10. • Example

11. Path diffrence
• path difference is the difference between the
distance travelled by two waves
Path difference

12. Relationship between path difference
and phase difference
• Path difference = wavelength x phase diffe
• x = λ/2
• Ex: find the path difference of two waves
where the phase difference between them is
2
x Ø
The wave length of the wave is 2m
Or x = λ/T x t

13. Wave properties
• Reflection
• Refraction
• Diffraction
• Interference
• Polarization

14. Speed of a wave
• Speed of a wave given by
v = f λ
Where f- frequency (s-1)
λ -wave length (m)
• Note : this equation can be applied for what
ever a wave motion speed calculation

15. Refection of waves
Laws of reflection
1. Incident ray reflected ray and the normal lies on same place
2. Incident angle equals to reflected angle ( i = r)
When the wave meets
a barrier or a surface
it bounce back is called
the reflection

16. Example: Find the angle of incident ray from the given information in picture?

17. Experiment
• When carrying out the experiment in ripple
tank following observations identified (refer
ripple tank function)
Barrier
Incident ray (water wave )
Reflected water wave

18. Refraction
• change in direction of propagation of any wave as a result of
its travelling at different speeds is called refraction
•

19. • Ripple tank experiment for refraction
Greater wavelength
Smaller wavelength
Note : frequency does not change when refraction occurs

20. • Laws of refraction
1. Incident ray, refracted ray and the normal drawn lie in the
same plane.
2.The sin of the angles between incident ray to refracted ray is a
constant this constant called refractive index (for that two
medium) sometimes called snell’s law
2nd law,
1n2 = sin i/ sin r
Medium 1
Medium 2
Medium 1 Medium 2
Note : always indicate from the light passing two mediums

21. Snell’s law defined another form as
1n2 = speed of wave in medium 1
speed of wave in medium 2
Medium 1
Medium 2
Note : when the wave passes from low dense to high dense the wave bend towards
Normal when wave passes from high dense to low dense the ray bends away from
normal
Bends away

22. • Example : find the refractive index for
following
ang = sin i /sin r
ang = sin 55 /sin 33
a - air
g- glass
Therefore refractive of air to glass
Is =…………………

23. • When the wave pass from high dense to low dense the refracted wave
bend away from normal
• When the incident angle increased at a particular angle of incidence the
refracted angle will go through the medium interface .the incident angle
at this point is called critical angle
When the incident angle increases critical angle (even .0000000…1) the ray will
reflect back to the medium this is called the total internal reflection
Reflection rules applied for TIR (TIR-total internal reflection)

24. Normally the refractive index
meant anm
Example : the refractive of water 1.33 meant
anw = 1.33 therefore wna = 1/1.33
ang = 1.55 gna = 1/1.55
Wng = wna x ang
Wng = 1/1.33 x 1.5
For critical angle calculations ..
Ex . Find crical angle of water
(refractive index 1.33)
Wna= sinc /sin 90
1/1.33 = sinc
C = sin-1(1/1.33)

26. find more simple problems at www.fixurscore.com

27. Condtions for TIR
• Wave should pass from high dense to low
dense
• Incident angle > critical angle (i > c)

28. • Sample Problem 3:
• Total Internal Reflection in Fiber Optics
Consider a optical fiber with the index of refraction of the inner core is 1.480 , and the
index of refraction of the outer cladding is 1.44.
A) What is the critical angle for the core-cladding interface?
B) For what range of angles in the core at the entrance of the fiber (q2) will the light be
completely internally reflected at the core-cladding interface?
C) What range of incidence angles in air does this correspond to?
D) If light is totally internally reflected at the upper edge of the fiber, will it necessarily
be totally internally reflected at the lower edge of the fiber (assuming edges are
parallel)
Solution
As before, we will need to combine Snell's Law with geometrical arguments.

29. Calculations;-

30. • Observations due to TIR
• Mirage formation
• Cat lights (at night ) (road signs)
Applications :
Fiber optics ,tail lights of vehicle , cut of
diamond faces ,prisms and periscopes ,

31. • Note :
Reflected wave inverted by
180 degrees
when a wave reflected by low dense -high dense medium
its inverted ,while high dense -low dense not inverted

32. Interference
• Wave interference is the phenomenon that occurs when two waves meet
while traveling along the same medium.
• . the interference of two or more waves of equal frequency and phase
producing a single amplitude equal to the sum of the amplitudes of the
individual waves this will lead to constructive and destructive interference
Constructive
Destructive
two conditions must be met:
The sources of the waves must
be coherent, which means they emit
identical waves with a constant
phase difference.
The waves should
be monochromatic - they should be
of a single wavelength.

33. Diffraction
• Diffraction which occur when a wave encounters an obstacle or a slit. It is
defined as the bending of light around the corners of an obstacle or
aperture
Obstacle

34. Diffraction can be increase by
• Reducing slit width
• When the gap size is equal to the wavelength, maximum diffraction occurs
and the waves spread out greatly - the wave fronts are almost semicircular

35. • Applications of diffraction and interference
X ray diffraction
Holograms (3D imaging)
Noise cancelling (passive noise )
Musical instrumentations (stationary waves )
Observations due to diffractions and
interference
Colored observations on CD

36. Young's single sit experiment
Wave fronts
( gap between wave fronts is wavelength)
Central maxima
Diffraction
Dark and bright fringes

37. • Experiment :-
When the monochromatic waves passed through a single slit the waves
will diffracted . This will make the waves go different distances .therefore
path different changes and which lead to constructive and destructive
interference pattern producing dark and bright fringes
Note :- . The central fringe is the only one where the entire aperture is adding
in phase, i.e. constructively. The next fringe will have 2/3 adding
constructively and 1/3 destructively, then after that 3/5 - 2/5, etc.

38. Path difference
Clear prove on class,,,,,,,

39. • A single slit experiment carried out to find the wave length of a unknown
source .the fringe number was 2 and it is the distance from the central
maxima is 0.002mm .the distance between slit and the screen was 20 cm .
Find the wavelength of the wave.(slit size is 0.2 micrometer and the bright
fringe located)
• Calculations:---

40. Young double slit experiment
difference in path length = dsin ϑ
then the condition for constructive
interference
dsin ϑ = mλ ,m = ± 1, ± 2,...
dsin ϑ = (m +1/2 ) λ m = ± 1, ± 2,..
sin ϑ = y/L (sin ϑ = tan ϑ)
y - coordinates of the bright and dark spots
y B
m = m λ L/d
y D
m = ( m+1/2) λ L/d
m= 3 1 2 0 -1 -2 -3

41. • Application of young's slits experiment
a) used to show wave interference
b) sending electron(s) through the double slits, makes the electrons
interfere with each other as if they were waves, this shows the wave
particle duality
c)Measure the wavelength of a wave
d)antireflection coatings on most complicated lenses
• Resolution and Diffraction
• Diffraction "blurs" images together, and places a limit on the finest details
one may distinguish this could be overcome by using
• Many slits (diffraction grating ) can be used

42. Standing waves
• standing wave, also called stationary wave, combination of two waves
moving in opposite directions, each having the
same amplitude and frequency
The three diagrams indicates a
formation of standing by incoming
and reflected waves
The minimum displacement of the medium particles is called nodes while the
maximum displaced position called antinodes

43. • When the standing waves formed resonance(loud identifiable sound )
occurs this can used to calculate the frequency of the wave
• Different types of standing waves are identified in different types of
instruments (string, air column)
• Different standing waves can be produced in the same instrument with
different frequencies this is called (harmonics )- the smallest frequency
called 1st harmonic or fundamental frequency /mode

44. Standing waves on string
λ/2
L = λ/2
2L = λ
We know that wave equation
v = f λ
f = v/2L
f0 = v/2L
fo = fundamental Mode ofr
1st harmonic
L –length of the string
The speed of the wave on the string
remain same

45. • Example ;
consider the first harmonic of a G string on a violin. The string is typically
made of nylon, having a density of ~1200 kg/m3. The diameter of the G
string is 4 mm. The string is held with a tension of 220 N. The frequency of
the first harmonic of the G string is 196 Hz. What is the length of the
string?
Speed in string
Is given
V = (T/µ)1/2
tension-T
µ - mass per unit length

46. L = 2 x λ /2
2L/2 = λ
V = f1 x λ
2V/2L = f1
The second resonance
will occur at 2V/2L = f1

47. L = 3 λ/2
2L/3 = λ
V = f λ
V = f2 x 2L/3
f2 = 3V/2L
f0 = v/2L f1 = 2V/2L f2 = 3V/2L
nth harmonic
Fn = n V /2L where
n=1,2,3………

48. • Standing waves in air columns
• One side closed tube
• When a standing wave is formed in a tube, the standing wave has a
maximum air displacement at the open end called an antinode
• At the closed end, there is no displacement; this is called a node, and the
air is halted
L = 5/4 λ
fo =v/4L
f1 =5V/L
1st harmonic
3rd harmonic (we don’t say second
Harmonic therefore 2nd harmonic)
5th harmonic
Prove……
Common formula
Fn = (2n+1)V/4L

50. • the longest standing wave in a tube of length L with two open ends has
displacement antinodes (pressure nodes) at both ends. It is called the
fundamental or first harmonic.
The next longest standing wave in a tube of length L with two open ends is thesecond
harmonic. It also has displacement antinodes at each end.
For a tube with two open ends all frequencies fn = nv/(2L) = nf1, with n equal
to an integer, are natural frequencies.

51. Polarization
• Polarized light waves are waves in which the vibrations occur in a single
plane. The process of transforming unpolarized light into polarized light is
known as polarization
The alignment of these molecules
gives the filter a polarization axis.
This polarization axis extends across
the length of the filter and only allows
vibrations of the electromagnetic
wave that are parallel to the axis to
pass through

52. Polarization by Reflection
• Unpolarized light can also undergo polarization by reflection off of nonmetallic
surfaces.
• nonmetallic surfaces such as asphalt roadways, snowfields and water reflect light
such that there is a large concentration of vibrations in a plane parallel to the
reflecting surface
• Fishermen know that the use of glare-reducing sunglasses with the proper
polarization axis allows for the blocking of this partially polarized light. By blocking
the plane-polarized light, the glare is reduced and the fisherman can more easily
see fish located under the water.

53. Problems
1. Suppose that light passes through two Polaroid filters whose polarization axes are
parallel to each other. What would be the result?
Solution:
The first filter will polarize the light, blocking one-half of its vibrations. The second
filter will have no affect on the light. Being aligned parallel to the first filter, the
second filter will let the same light waves through.
2. Light becomes partially polarized as it reflects off nonmetallic surfaces such as glass,
water, or a road surface. The polarized light consists of waves vibrate in a plane
that is ____________ (parallel, perpendicular) to the reflecting surface
Solution: Parallel
Reflected light becomes partially polarized in a plane which is parallel to
thereflecting surface.
3. Consider the three pairs of sunglasses below. Identify the pair of glasses is capable
of eliminating the glare resulting from sunlight reflecting off the calm waters of a
lake? _________ Explain. (The polarization axes are shown by the straight lines.)

54. solution: A
Referring to the above question, the glare is the result of a
large concentration of light aligned parallel to the water
surface. To block such plane-polarized light, a filter with a
vertically aligned polarization axis must be used
Note : electro magnetic waves can be polarized not other waves such as
gravitational or sound
Common applications of polarizers:
• Contrast enhancement display filters
• Sunlight readable touch screens
• Photography
• Stress analysis of glass and plastics
• Optical sensors and safety light curtains
• 3D projection systems

55. Applications of polarization
• Polaroids are used in sun glasses. They reduce the intensity and the glare
by cutting down the horizontally polarized light.
• Polarized light is used in photo elastic stress analysis.
• For 3-D view, special type of glasses, which have polaroids with
• perpendicular axes, are used.
• Polarized light is useful to determine size and shape of viruses.
• This polarized light finds many practical applications in industry and
engineering science.
.

56. Ultra sound and Applications
• Ultrasound uses high frequency sounds that are higher than the human ear can
hear. ie. 20 000 Hz.
• higher frequencies of ultrasound have short wavelengths and are absorbed easily and
therefore are not as penetrating. For this reason high frequencies are used for scanning areas
of the body close to the surface and low frequencies are used for areas that are deeper down
in the body. These frequencies generally range between 1-50 MHz.
Ultrasound is produced and detected
using an ultrasound transducer.
Ultrasound transducers are capable
of sending an ultrasound and
then the same transducer
can detect the sound and convert
it to an electrical signal to be diagnosed.
Because different types of tissues in body
Absorb and reflect different intensities of ultra sound
This idea used to obtain images such as
fetus, stones in bladder ect

57. Doppler effect
• The Doppler effect is observed whenever the source of waves
is moving with respect to an observer
• The Doppler effect can be observed for any type of wave -
water wave, sound wave, light wave, etcct to an observer
When the distance between the source
producing waves and receiver which
receives waves increase the frequency of
the received wave forms is lower than the
frequency of the source wave form
When the source which produces the waves
and receiver distance decreases, the t
frequency of the wave received larger than of
Producesd wave this effect is called Doppler
effect

58. Where c- speed of the wave in medium
v –source speed (ambulance ,police siren)