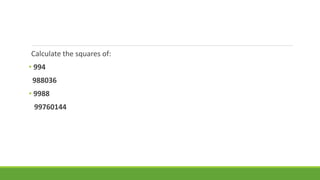
The document provides an introduction to Vedic mathematics, which is based on ancient Indian Vedic texts. It describes several Vedic mathematical formulas with examples, such as Ekadhikena Purvena for calculating squares, Nikhilam navatascaramam Dasatah for multiplication involving 9s, and Yavadunam Tavadunikrtya Varganca Yojayet for calculating squares close to bases of powers of 10. Algebraic proofs are also presented for some of the formulas. The document notes that Vedic math techniques can solve difficult math problems with high speed and accuracy, and represents just the beginning of applications of Vedic mathematics.

1. VEDIC MATHEMATICS

2. Introduction
• Author – Bharati Krishna Tirthaji
• Based on Vedas
• Vedic Maths

3. Ekadhikena Purvena
By one more than the previous one
Calculate the square of 45.

4. Multiply the previous digit by one more than itself
452 = 4X5 and 25
= 2025

5. Calculate the square of:
• 35
1225
•165
27225

6. Algebraic Proof
• (ax + b)2 = a2x2 + 2abx + b2
• x=10 and b=5
• (10a + 5)2 = 100a2 + 100a + 25
= 100(a)(a+1) + 25

7. Multiplication of two numbers with sum of unit
digits=10 and same rest of the number
Calculate the product of 67 and 63.

8. Multiply the previous digits by one more than itself and add it to product of unit digits
67 X 63 = 6 X 7 and 7 X 3
= 4221

9. Calculate:
• 12 X 18
216
• 112 X 118
13216

10. Algebraic Proof
• (ax + b)(ax + c) = a2x2 + ax(b+c) + bc
• x=10 and b+c=10
• (10a + b)(10a + c) = 100a2 + 100a + bc
= 100(a)(a+1) + bc

11. Nikhilam navatascaramam Dasatah
All from 9 and the last from 10
Calculate the product of 94 and 97.

12. Base – 10, 100, 1000, etc.
Deviation – Subtract all from 9 and the last from 10
94 - 6
97 - 3
= 9118

13. Calculate:
• 98 X 97
9506
• 987 X 990
977130

14. Calculate
• 14 X 12
168
• 998 X 1025
1023000 – 50
1022950

15. Algebraic Proof
• Base = x, Numbers = a and b
• a=x-d1, b=x-d2
• a X b = (x-d1) X (x-d2)
= x2 – xd1 – xd2 + d1d2
= x(x – d1 –d2) + d1d2
= x(a – d2) + d1d2

16. Ekanyunena Purvena
One Less than the previous
Calculate the product of 15 X 999

17. Useful in multiplication with 9, 99, 999, 9999 and so on
15 X 999 = 15 – 1 =14
999 – 14 =985
= 14985
877 X 9999 = 877 – 1 = 876
9999 – 876 = 9123
= 8769123

18. Calculate:
• 64 X 99
6336
• 3251 X 9999
32506749

19. Algebraic Proof
• Numbers = a and b
• a is of form (10x + y) and b is 9, 99, 999….
• (10x + y) X 99 = (10x + y) X (100-1)
= 10(x)(10)2 – 10x + (y)102 – y
= (x)(10)3 + y(10)2 – (10x + y)
= (x)(10)3 + (y-1)(10)2 + (102 – (10x + y))
= (x)(10)3 + (y-1)(10)2 + (99 – (a-1))

20. Yavadunam Tavadunikrtya Varganca Yojayet
What ever the deficiency subtract that deficit from the number and write along
side the square of that deficit
Calculate the square of 96

21. Useful in obtaining squares of numbers close to bases of powers of 10
962 -> Base = 100
Deficit = 100-96 =4
96-4 =92 and 42 = 16
= 9216

22. Calculate the squares of:
• 994
988036
• 9988
99760144

23. Algebraic Proof
• Numbers = a and b
• a is of form (b-d) and b is 10,100,1000,……..
• a2 = (b-d)2 = b2 – 2bd + d2
= b(b – 2d) + d2
= b(b – d – d) + d2
= b(a – d) + d2

24. Calculate the square of 476

25. Base = 500 = 5 X 100 Base = 500 = 1000/2
4762 -> Deficit = 24 452/2 = 226
476 – 24 = 452 Ans = (226 X 1000) + 576
452 X 5 = 2260 = 226576
242 = 576
Ans = (2260 X 100) + 576
= 226576

26. Calculate the square of:
• 395
156025
• 68
4624

27. Beejank
Sum of digits of a number
Beejank of 72 = 9,
47 = 1+1 = 2,
68123 = 2+0 = 2
894563912 = 2

28. Gunita Samuccayah
The whole product is same
67 + 76 = 143
Beejank(67) = 4, 76 =4 and 143 =8
4762 = 226576
Beejank(476) = 8, Beejank(8 X 8) = 1
Beejank(226576) = 1

29. Just The Beginning
• Vast scope of Vedic Maths
• Solves difficult problems with high speed and accuracy

30. THANK YOU 