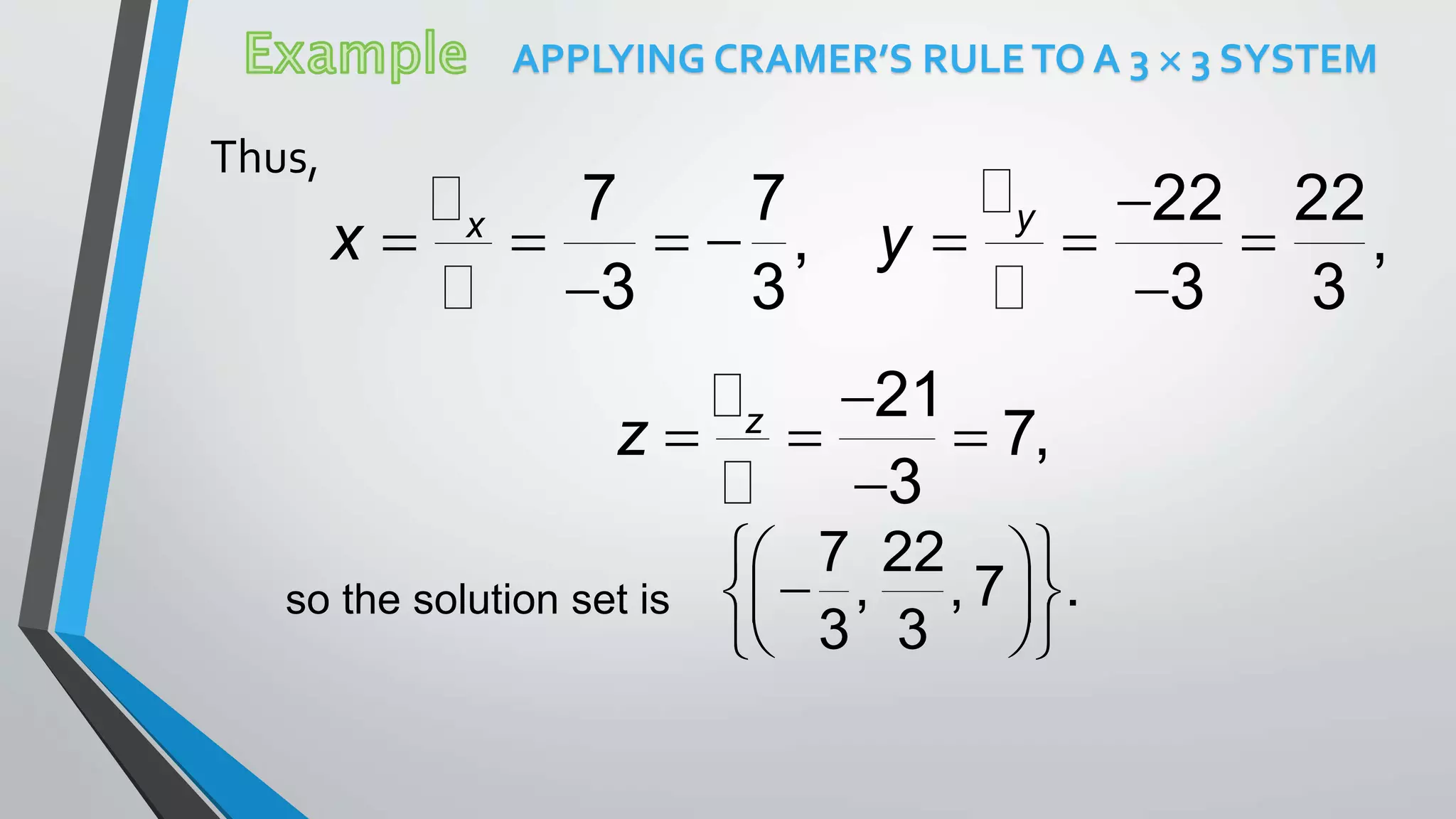
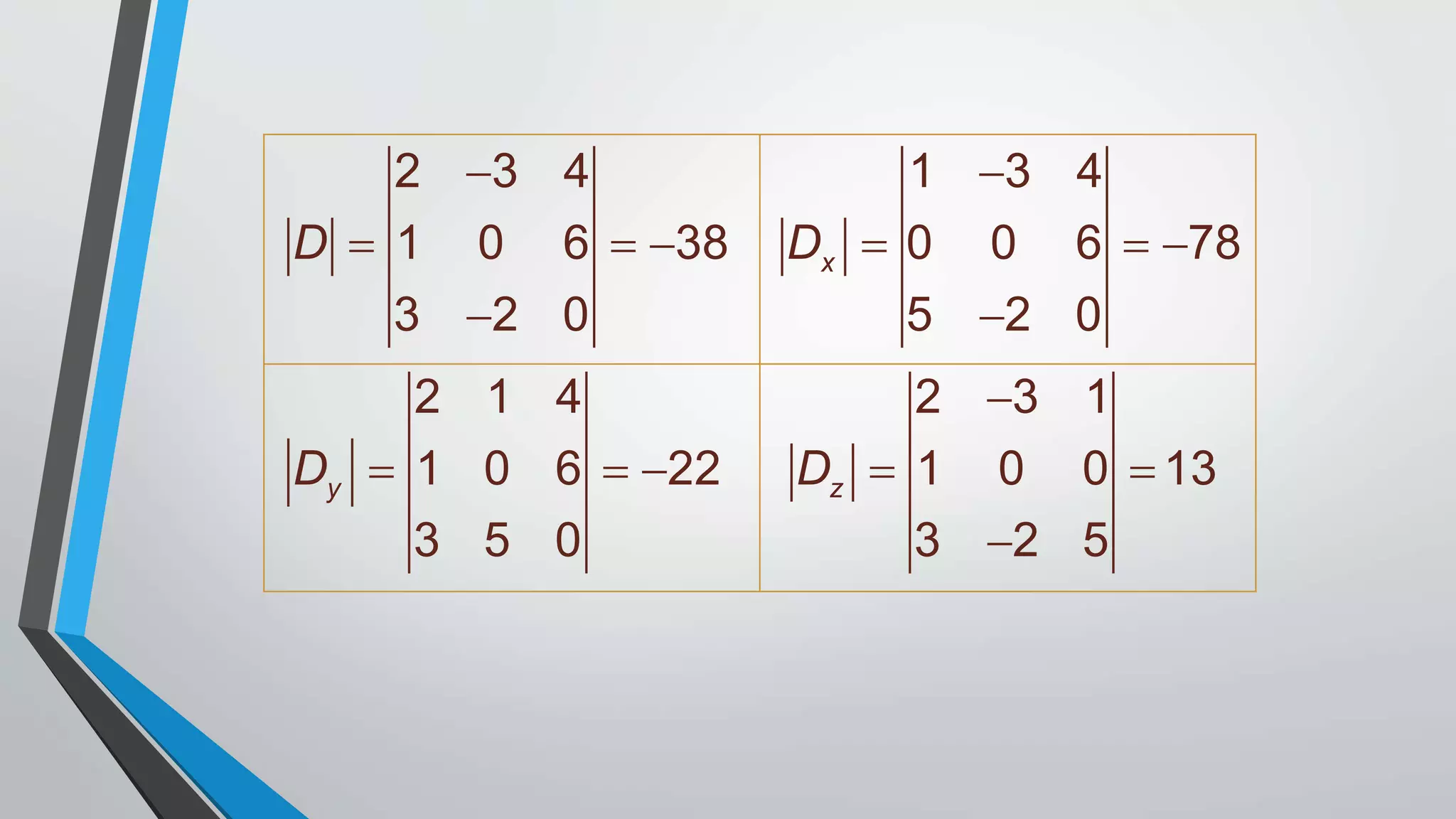
This document defines determinants and provides examples of calculating determinants of 2x2 and 3x3 matrices. It introduces key terminology like minors, cofactors, and expands on Cramer's rule for solving systems of linear equations using determinants. The document explains that the determinant of a square matrix is a single number associated with the matrix, and provides rules and examples for calculating determinants by summing the products of elements and their cofactors.

1. 2018
Lecture №1
DETERMINANTS
Dobroshtan Оlena

3. If a matrix is square (that is, if it has the
same number of rows as columns), then we
can assign to it a number called its
determinant.

4. Associated with every square matrix is a real
number called the determinant of A. In this
text, we use det A.
.aaaaA 12212211 det
The determinant of a 2 × 2 matrix A, is
defined as

11 12
21 22
a a
A
a a

6. If A =
 
 
 
11 12
21 22
, then
a a
a a
 11 12
21
11 22 2 12
22
1 .a a aA
a
a
a a
a

7. Matrices are enclosed with round
brackets, while determinants
are denoted with vertical bars.
A matrix is an array of numbers, but its
determinant is a single number.

8. The arrows in the following diagram will remind
you which products to find when evaluating a 2  2
determinant.
11 12
21 22
a a
a a

9. Example 1 EVALUATING A 2  2 DETERMINANT
Let A =
3 4
.
6 8
 
 
 
Find A.
Solution
Use the definition with
    22212 111 , ,43 6, .8aaa a
  8 463A
a11 a22 a21 a12
  24 24  48

10. Determinant of a 2 x 2 Matrix


6 3
2 3
 
  
 
6 3
2 3
A
Evaluate | A | for
   6 3 ( 3)2   18 ( 6) 24

11. If A =
11 12 13
21 22 23
31 32 33
, then
a a a
a a a
a a a
 
 
 
  
11 12 13
21 22 23 11 22 33 12 23 31 13 21 32
31 32 33
( )
a a a
A a a a a a a a a a a a a
a a a
   
31 22 13 32 23 11 33 21 12( ).a a a a a a a a a  

13. The determinant of each 2  2 matrix above is
called the of the associated element in the
3  3 matrix.
The symbol represents ,the minor that results
when row i and column j are eliminated.

14. 22 23
11
32 33
a a
M
a a
 
  
 
12 13
21
32 33
a a
M
a a
 
  
 
12 13
31
22 23
a a
M
a a
 
  
 
11 13
22
31 33
a a
M
a a
 
  
 
11 12
23
31 32
a a
M
a a
 
  
 
11 12
33
21 22
a a
M
a a
 
  
 

15. The minor M12 is the determinant of the matrix
obtained by deleting the first row and second
column from A.
 

12
2 3 1
0 2 4
2 5 6
M 

0 4
2 6
  0(6) 4( 2) 8
For , A is the matrix
 
 
 
 
 
2 3 1
0 2 4
2 5 6

16. Let Mij be the for element aij in an n  n
matrix.
The of aij, written as Aij, is

 ( 1) .i j
ij ijA M

17. Find the cofactor of each of the following elements
of the matrix  
 
 
 
 
3
1 2 0
6 2
98
4
a. 6
Solution
Since 6 is in the first
row, first column of the
matrix, i = 1 and j = 1 so 11
9 3
6.
2 0
M   
The cofactor is
1 1
( 1) ( 6) 1( 6) 6.
     

18. Find the cofactor of each of the following elements
of the matrix  
 
 
 
 
3
1 2 0
6 2
98
4
Solution
The cofactor is
b. 3
Here
i = 2 and j = 3 so, 23
6 2
10.
1 2
M  
2 3
( 1) (10) 1(10) 10.
    

19. Find the cofactor of each of the following elements
of the matrix  
 
 
 
 
3
1 2 0
6 2
98
4
Solution
The cofactor is
c. 8
We have,
i = 2 and j = 1 so, 21
2 4
8.
2 0
M   
2 1
( 1) ( 8) 1( 8) 8.
     

20. •Similarly,
•
• So, A33 = (–1)3+3 M33 = 4
33
2 3 1
2 3
0 2 4 2 2 3 0 4
0 2
2 5 6
M

      


21. Multiply each element in any row or column of
the matrix by its cofactor.
The sum of these products gives the value of the
determinant.
11 12 1
21 22 2
1 2
11 11 12 12 1 1
det( )
...
n
n
n n nn
n n
a a a
a a a
A A
a a a
a A a A a A
 
   

22. Evaluate
  
   
 
  
2 3 2
1 4 3 ,
1 0 2
by the
.
Solution
12
1 3
1(2) ( 1) 3)
1 2
5(M
 
       

22
2 2
2(2) ( 1)( 2)
1 2
2M

     

32
2 2
2( 3) ( 1)( 2)
1 3
8M

      



Use
parentheses, &
keep track of
all negative
signs to avoid
errors.

23. Evaluate
  
   
 
  
2 3 2
1 4 3 ,
1 0 2
by the
.
Solution
Now find the cofactor of each element of
these minors.
12
1 2
12
3
( 1) ( 1) ( 5) ( 5) 51MA 
        
2
22
42
22 ( 1) ( 1) (2) 1 2 2MA 
     
32
3 2
32
5
( 1) ( 1) ( 8) ( 8) 81MA 
        

24. Evaluate
  
   
 
  
2 3 2
1 4 3 ,
1 0 2
by the
.
Solution
Find the determinant by multiplying each cofactor by its
corresponding element in the matrix and finding the sum of these
products.
12 12 2 32 2 222 3
2 2
1
1 2
4 3
3
0
a A aA Aa
 
    

(5) ( )2 (8043 )  
15 ( 8) 0 23      

25.  
 
  
  
2 3 1
0 2 4
2 5 6
A

 

2 3 1
det( ) 0 2 4
2 5 6
A    
 
2 4 0 4 0 2
2 3 ( 1)
5 6 2 6 2 5
               2(2 6 4 5) 3 0 6 4( 2) 0 5 2( 2)
    16 24 4 44

26.  
 
  
  
2 3 1
0 2 4
2 5 6
A
Expanding by the second row, we get:

  

2 3 1
det( ) 0 2 4
2 5 6
A
 
   
 
3 1 2 1 2 3
0 2 4
5 6 2 6 2 5
            0 2 2 6 ( 1)( 2) 4 2.5 3( 2)
    0 20 64 44

27.  
 
  
  
2 3 1
0 2 4
2 5 6
A
Expanding by the third column, we get:

  

2 3 1
det( ) 0 2 4
2 5 6
A    
 
0 2 2 3 2 3
1 4 6
2 5 2 5 0 2
                 0 5 2( 2) 4 2 5 3( 2) 6 2.2 3 0
     4 64 24 44

29. The solutions of linear equations can sometimes be
expressed using determinants.
To illustrate, let’s solve the following pair of linear
equations for the variable x.
ax by r
cx dy s
 

 

30. •    x y
a b r b a r
c d s d c s
 and
yx
x y
Using the notation
the solution of the system can be written as:

31. 2 6 1
8 2
x y
x y
  

 
Use Cramer’s Rule to solve the system.

32. For this system, we have:
     
2 6
2 8 6 1 10
1 8

      
1 6
( 1)8 6 2 20
2 8
x

     
2 1
2 2 ( 1)1 5
1 2
y

33.  
   
20
2
10
x
x

  
5 1
10 2
y
y
The solution is:

34. Cramer’s Rule can be extended
to apply to any system of n linear
equations in n variables in which
the determinant of the
coefficient matrix is not zero.

35.      
     
     
     
     
          
11 12 1 1 1
21 22 2 2 2
1 2
n
n
n n nn n n
a a a x b
a a a x b
a a a x b
As we saw in the preceding section, any such
system can be written in matrix form as:

36. Caution As indicated in the
preceding box, Cramer’s rule does not
apply if D = 0. When D = 0 the system is
inconsistent or has infinitely many
solutions. For this reason, evaluate D first.

37. APPLYING CRAMER’S RULE TO A 2  2 SYSTEM
Use Cramer’s rule to solve the system
5 7 1
6 8 1
x y
x y
  
 Solution
By Cramer’s rule, and Find Δ
first, since if Δ = 0, Cramer’s rule does not
apply. If
Δ ≠ 0, then find Δx and Δy.
    
5 7
5(8) 6(7)
6 8
2  

   
1 7
1(8) 1(7)
1 8
15x

    
5 1
5(1) 6( 1)
6 1
11y

38. APPLYING CRAMER’S RULE TO A 2  2 SYSTEM
By Cramer’s rule,
     




15 11
and
2 2
1
.
11
2 2
5 yx
x y

39. Let an n  n system have linear equations of the form
1 1 2 2 3 3 .n na x a x a x a x b    
Define D as the determinant of the n  n matrix of all
coefficients of the variables. Define Dx1 as the determinant
obtained from D by replacing the entries in column 1 of D with
the constants of the system. Define Dxi as the determinant
obtained from D by replacing the entries in column i with the
constants of the system. If D  0, the unique solution of the
system is    31 2
1 2 3, , , , .xx x xn
n
D
x x x x
D

40. APPLYING CRAMER’S RULETO A 3  3 SYSTEM
Use Cramer’s rule to solve the system.
   

   
    
2 0
2 5 0
2 3 4 0
x y z
x y z
x y z
Solution Rewrite each
equation in the form
ax + by + cz + = k.

41. APPLYING CRAMER’S RULETO A 3  3 SYSTEM
Verify that the required determinants are

   

1 1 1
2 1 1 3,
1 2 3
 
    

2 1 1
5 1 1 7,
4 2 3
x
 
   
1 2 1
2 5 1 22,
1 4 3
y

     

1 1 2
2 1 5 21
1 2 4
z

42. APPLYING CRAMER’S RULETO A 3  3 SYSTEM
Thus,

      
 
7 7 22 22
, ,
3 3 3 3
yx
x y

  

21
7,
3
z
z
so the solution set is
7 22
, , 7 .
3 3
  
  
  

43. SHOWING THAT CRAMER’S RULE DOES NOT APPLY
Show that Cramer’s rule does not apply to the following system.
  

  
   
2 3 4 10
6 9 12 24
2 3 5
x y z
x y z
x y zSolution
We need to show that Δ = 0. Expanding about column 1 gives
2 3 4
9 12 3 4 3 4
6 9 12 2 6 1
2 3 2 3 9 12
1 2 3
D

  
    
  

2(3) 6(1) 1(0 0) .   
Since D = 0, Cramer’s rule does not apply.

44. Note When D = 0, the system is either
inconsistent or has infinitely many solutions.

45. Use Cramer’s Rule to solve the system.
First, we evaluate the determinants that appear in Cramer’s
Rule.
2 3 4 1
6 0
3 2 5
x y z
x z
x y
  

 
  

46. 2 3 4 1 3 4
1 0 6 38 0 0 6 78
3 2 0 5 2 0
2 1 4 2 3 1
1 0 6 22 1 0 0 13
3 5 0 3 2 5
x
y z
D D
D D
 
     
 

    


47. 78 39
38 19
22 11
38 19
13 13
38 38
x
y
z
D
x
D
D
y
D
D
z
D

  


  

   

Now, we use Cramer’s Rule to get the solution:

48. However, in systems with more than three equations,
evaluating the various determinants involved is usually a
long and tedious task.
Moreover, the rule doesn’t apply if | D | = 0 or if D is not a
square matrix.
So, Cramer’s Rule is a useful alternative to
Gaussian elimination—but only in some
situations.