This document provides instructions and examples for using a TI-83/84 graphing calculator. It covers how to graph equations, systems of equations, and linear inequalities. It also demonstrates how to calculate the correlation coefficient between two data sets using the calculator. Examples are provided to illustrate graphing linear and exponential functions, finding points of intersection for systems of equations, and interpreting correlation values. Key steps are outlined for entering data and functions into the calculator to perform graphing and statistical analysis.

1. Using the TI Graphing
Calculator

2. “Using the TI 83 84 Graphing Calculator”
About 55,200 results

4. Contents
• Graphing an Equation
• Graphing Systems of Linear Equations
• Graphing Linear Inequalities
• Calculating Correlation Coefficient
• Finding a Regression Equation

5. Graphing Equations Using a TI-83/84:
Step 1: Press [Y=] and key in the equation using
[X, T, Θ, n] for x.
Step 2: Press [WINDOW] to change the viewing
window, if necessary.
Step 3: Enter in appropriate values for Xmin, Xmax,
Xscl, Ymin, Ymax, and Yscl, using the arrow
keys to navigate.
Step 4: Press [GRAPH].
• 1.3.1: Creating and Graphing Linear Equations in Two Variables
5

6. Example 1
A Boeing 747 starts out a long flight with about 57,260
gallons of fuel in its tank. The airplane uses an
average of 5 gallons of fuel per mile. Write an
equation that models the amount of fuel in the tank
and then graph the equation using a graphing
calculator.
6

7. Example 1, continued
Substitute the slope and y-intercept into the equation
y = mx + b, where m is the slope and b is the y-
intercept.
m = 5
b = 57,260
y = –5x + 57,260
7

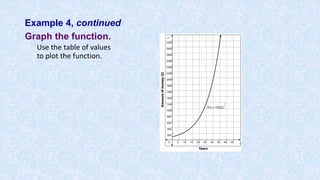
8. Example 1, continued
Graph the equation on your calculator.
On a TI-83/84:
Step 1: Press [Y=].
Step 2: At Y1, type in [(–)][5][X, T, Θ,
n][+][57260].
Step 3: Press [WINDOW] to change the viewing
window.
Step 4: At Xmin, enter [0] and arrow down 1
level to Xmax.
Step 5: At Xmax, enter [3000] and arrow down 1
level to Xscl.

9. Example 1, continued
Redraw the graph on graph paper.
On the TI-83/84, the scale was entered in [WINDOW]
settings. The X scale was 100 and the Y scale was
1,000.
Set up the graph paper using these scales. Label the
y-axis “Fuel used in gallons.” Show a break in the
graph from 0 to 40,000 using a zigzag line. Label the
x-axis “Distance in miles.”
To show the table on the calculator so you can plot
points, press [2nd][GRAPH]. The table shows two
columns with values; the first column holds the x-
values, and the second column holds the y-values.

10. Example 1, continued
Pick a pair to plot, and then connect the line. To
return to the graph, press [GRAPH]. Remember to
label the line with the equation.
(Note: It may take you a few tries to get the window
settings the way you want. The graph that follows
shows an X scale of 200 so that you can easily see
the full extent of the graphed line.)

11. Guided Practice: Example 1, continued

12. Example 2
An investment of $500 is compounded monthly at a rate
of 3%. What is the equation that models this situation?
Graph the equation.

13. Example 2, continued
Read the problem statement and then reread
the scenario, identifying the known quantities.
Initial investment = $500
r = 3%
Compounded monthly = 12 times a year

14. Example 2, continued
Substitute the known quantities into the
general form of the compound interest
formula.
In this formula, , P is the initial value, r is
the interest rate, n is the number of times the
investment is compounded in a year, and t is the
number of years the investment is left in the account
to grow.
A = P 1+
r
n
æ
è
ç
ö
ø
÷
nt

15. Example 2, continued
P = 500
r = 3% = 0.03
n = 12
A = P 1+
r
n
æ
è
ç
ö
ø
÷
nt
A = 500 1+
0.03
12
æ
è
ç
ö
ø
÷
12t
A = 500(1.0025)12t

16. Example 2, continued
Notice that, after simplifying, this form is similar to
y = abx. To graph on the x- and y-axes, put the
compounded interest formula into this form, in which
A = y, P = a, , and t = x.
A = 500(1.0025)12t becomes y = 500(1.0025)12x.
1+
r
n
æ
è
ç
ö
ø
÷ = b

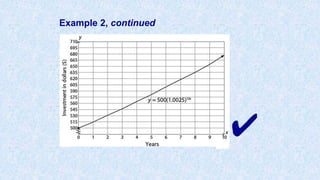
17. Example 2, continued
Graph the equation using a graphing calculator.
On a TI-83/84:
Step 1: Press [Y=].
Step 2: Type in the equation as follows:
[500][×][1.0025][^][12][X, T, Θ, n]
Step 3: Press [WINDOW] to change the
viewing window.
Step 4: At Xmin, enter [0] and arrow down
1 level to Xmax.
Step 5: At Xmax, enter [10] and arrow
down 1 level to Xscl.

18. Example 2, continued
Step 6: At Xscl, enter [1] and arrow down 1 level to
Ymin.
Step 7: At Ymin, enter [500] and arrow down 1
level to Ymax.
Step 8: At Ymax, enter [700] and arrow down 1
level to Yscl.
Step 9: At Yscl, enter [15].
Step 10: Press [GRAPH].

19. Example 2, continued
Transfer your graph from the screen to
graph paper.
Use the same scales that you set for your viewing
window.
The x-axis scale goes from 0 to 10 years in
increments of 1 year.
The y-axis scale goes from $500 to $700 in
increments of $15. You’ll need to show a break in
the graph from 0 to 500 with a zigzag line, as
shown in the graph that follows.

20. Example 2, continued
✔

21. Example 3
Create a table of values for the exponential function
. Identify the asymptote and y-intercept of
the function. Plot the points and sketch the graph of the
function, and describe the end behavior.
f(x) = 4
2
3
æ
è
ç
ö
ø
÷
x
-3

22. Example 3, continued
Create a table of values.
Choose values of x and solve for the corresponding values
of f(x).
x f(x)
–4 17.25
–2 6
0 1
2 –1.22
4 –2.2099
f(x) = 4
2
3
æ
è
ç
ö
ø
÷
x
-3

23. Example 3, continued
Identify the asymptote of the function.
The asymptote of the function is always the
constant, k.
In the function , the value of
k is –3.
The asymptote of the function is y = –3.
f(x) = 4
2
3
æ
è
ç
ö
ø
÷
x
-3

24. Example 3, continued
Determine the y-intercept of the function.
The y-intercept of the function is the value of f(x) when x is equal to 0.
It can be seen in the table that when x = 0, f(x) = 1.
The y-intercept is (0, 1).

25. Example 3, continued
Graph the function.
Use the table of values
to create a graph of the
function.

26. Example 3, continued
Describe the end behavior of the graph.
The end behavior is what happens at the ends of
the graph.
As x becomes larger, the value of the function approaches the asymptote, –3.
As x becomes smaller, the value of the function approaches infinity.
Since the function approaches infinity
as x becomes smaller, the graph shows
exponential decay.
✔

27. Example 4
You deposit $100 into a long-term certificate of deposit
(CD) in which your money will double every 7 years.
1. Write a function to show how much money you will
have in total in 7, 14, 21, 28, and 35 years.
2. Use the function to create a table
3. Graph the function.
4. What do the parameters represent in the context of
this problem?

28. Example 4, continued
Write a function.
This scenario is represented by an exponential function.
• The initial deposit is $100.
• Your money doubles every 7 years, so the growth factor is 2.
• The time period is 7 years.
Substitute these values into the exponential function.
The function for this scenario is .f(x) =100(2)
x
7

29. Example 4, continued
Create a table.
Let x = the number of years and f(x) = the amount of
money in dollars.
Use the values 7, 14, 21, 28, and 35 for x.

30. Example 4, continued
x f(x)
7 200
14 400
21 800
28 1600
35 3200
100(2)
x
7
100(2)
7
7
100(2)
14
7
100(2)
21
7
100(2)
28
7
100(2)
35
7

31. Example 4, continued
Graph the function.
Use the table of values
to plot the function.

32. Example 4, continued
Identify the parameters.
The parameters in this problem are the starting amount of $100 and the
growth rate of 2.
✔

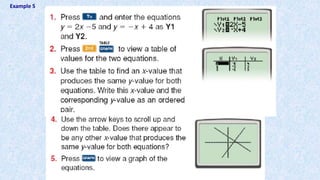
33. Graphing Systems of Equations Using a TI-83/84:
Step 1: Press [Y=] and key in the equation using
[X, T, Θ, n] for x.
Step 2: Press [ENTER] and key in the second equation.
Step 3: Press [WINDOW] to change the viewing window, if
necessary.
Step 4: Enter in appropriate values for Xmin, Xmax, Xscl,
Ymin, Ymax, and Yscl, using the arrow keys to
navigate.
Step 5: Press [GRAPH].
Step 6: Press [2ND] and [TRACE] to access the Calculate
Menu.
Step 7: Choose 5: intersect.
Step 8: Press [ENTER] 3 times for the point of intersection.

34. Example 5

35. Solve the system: y = -2x + 9 and y = 3x - 4
1. Enter the first equation into Y1.
2. Enter the second equation into Y2.
3. Hit GRAPH.
4. Use the INTERSECT option to find where the
two graphs intersect (the answer).
2nd TRACE (CALC) #5 intersect
Move spider close to the intersection.
Hit ENTER 3 times.
5. Answer: x = 2.6 and y = 3.8
Let’s do another one.
Example 6

36. Graphing Linear Inequalities Using a TI-83/84:
Step 1: Press [Y=] and arrow over to the left two times so that
the cursor is blinking on the “”.
Step 2: Press [ENTER] two times for the greater than icon “ ”
and three times for the less than icon “ ”.
Step 3: Arrow over to the right two times so that the cursor is
blinking after the equal sign.
Step 4: Key in the equation using [X, T, Θ, n] for x.
Step 5: Press [WINDOW] to change the viewing window, if
necessary.
Step 6: Enter in appropriate values for Xmin, Xmax, Xscl, Ymin,
Ymax, and Yscl, using the arrow keys to navigate.
Step 7: Press [GRAPH].

37. Example
Example 7

38. Calculating and Interpreting the Correlation Coefficient
The correlation coefficient, r, is a quantity that allows us to
determine how strong this relationship is between two events.
It is a value that ranges from –1 to 1; a correlation coefficient of –1
indicates a strong negative correlation, a correlation coefficient of 1
indicates a strong positive correlation, and a correlation coefficient
of 0 indicates a very weak or no linear correlation.
Note that a correlation between two events does not imply that
changing one event causes a change in the other event—only that
a change might have taken place in the other event. This will be
explored more later.

39. Continued

40. Continued
n X X2 Y Y2 XY
1 2 3
2 4 4
3 6 7
4 8 6
5 10 9
Σ

41. Key Concepts, continued

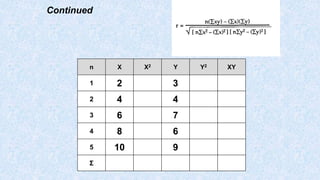
42. On a TI-83/84:
You can use a calculator to calculate the correlation coefficient.
Step 1: Set up the calculator to find correlations. Press
[2nd], then [CATALOG] (the “0” key). Scroll down and
select DiagnosticOn, then press [ENTER]. (This step
only needs to be completed once; the calculator will
stay in this mode until changed in this menu.)
Step 2: To calculate the correlation coefficient, first enter the
data into a list. Press [2nd], then L1 (the “1” key).
Scroll to enter data sets. Press [2nd], then L2 (the “2”
key). Enter the second event in L2.
Step 3: Calculate the correlation coefficient. Press [STAT],
then select CALC at the top of the screen. Scroll
down to 8:LinReg(a+bx), and press [ENTER].
The r value (the correlation coefficient) is displayed along
with the equation.
X Y
2 3
4 4
6 7
8 6
10 9

43. Example 9:
Andrew wants to estimate his gas
mileage, or miles traveled per
gallon of gas used. He records the
number of gallons of gas he
purchased and the total miles he
traveled with that gas.
What is the correlation between the number
of gallons purchased and the total miles
He traveled?
Gallons Miles
15 313
17 340
18 401
19 423
18 392
17 379
20 408
19 437
16 366
20 416

44. Example 9, continued
Create a scatter plot of the data.
Let the x-axis represent the number of gallons
purchased and the y-axis represent the miles
traveled.
Miles
Gallons

45. Example 9, continued
Analyze the scatter plot, and describe any
relationship between the two events.
As the number of gallons increases, the miles also
increase. The shape of the graph is approximately a
line, and it appears there is a positive linear
correlation between gallons and miles.

46. Example 9, continued
Find the correlation coefficient using a
graphing calculator. Follow the steps in the
Key Concepts section.
r = 0.872

47. Example 9, continued
Describe the correlation between the two
events.
0.872 is close to 1. There is a strong positive linear
correlation between the gallons purchased and the
miles traveled.

48. Find a Regression Equation
• A graphing calculator can graph a scatter plot of given data and find a
regression equation that models the given data.
• Begin by entering the data into lists on your calculator, as outlined in the
following steps.
• Decide whether the data would best be modeled with a quadratic
regression, linear regression, or exponential regression. (In this lesson,
we focus on quadratic regressions, but you can choose the type of
regression that is most appropriate for the situation.)
• To decide which regression model is best, look at the scatter plot of the
data you entered.
• After you find the appropriate model using your calculator, you can graph
this equation on top of the scatter plot to verify that it is a reasonable
model.

49. Example 10: Linear Regression
Andrew wants to estimate his gas
mileage, or miles traveled per
gallon of gas used. He records the
number of gallons of gas he
purchased and the total miles he
traveled with that gas.
Use your calculator to make a scatter
plot of the data in the table and to find a
linear regression of this data.
Gallons Miles
15 313
17 340
18 401
19 423
18 392
17 379
20 408
19 437
16 366
20 416

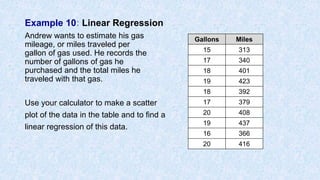
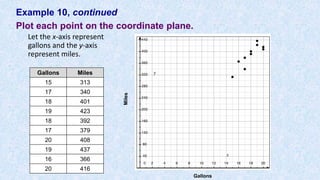
50. Example 10 continued
Create a scatter plot showing the relationship
between gallons of gas and miles driven.
Gallons Miles
15 313
17 340
18 401
19 423
18 392
17 379
20 408
19 437
16 366
20 416
Step 1: Press [STAT].
Step 2: Press [ENTER] to select Edit.
Step 3: Enter x-values into L1.
Step 4: Enter y-values into L2.
Step 5: Press [2nd][Y=].
Step 6: Press [ENTER] to turn on Stat Plot,
Step 7: For Plot 1, press [ENTER] to turn on; scroll down to TYPE select type
scatter plot. (optional: select lists and MARK).
Step 7: Press [ZOOM][9] to select ZoomStat and show the scatter plot.

51. Example 10, continued
Plot each point on the coordinate plane.
Let the x-axis represent
gallons and the y-axis
represent miles.
Miles
Gallons
Gallons Miles
15 313
17 340
18 401
19 423
18 392
17 379
20 408
19 437
16 366
20 416

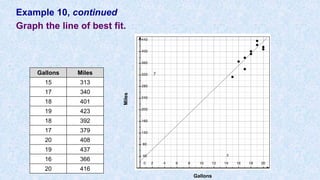
52. Example 10, continued
• Your graphing calculator can help you to find a linear regression model
after you input the data.
Entering Lists Using a TI-83/84:
Step 1: Press [STAT].
Step 2: Arrow to the right to select Calc.
Step 3: Press [5] to select LinReg.
Step 4: At the LinReg (a + bx) screen, Press [ENTER]
y = a + bx
a = 24.10843373
b = 20. 30120482
Step 5: Press [y=] and enter regression equation y = 20.3x + 24.1
Step 6: Press [GRAPH]

53. Example 10, continued
Graph the line of best fit.
Miles
Gallons
Gallons Miles
15 313
17 340
18 401
19 423
18 392
17 379
20 408
19 437
16 366
20 416

54. Example 11
The students in Ms. Swan’s class surveyed people of all
ages to find out how many people in each of several age
groups exercise on a regular basis. Their data is shown
in the table on the next slide.
Use your calculator to make a scatter plot of the data in
the table and to find a quadratic regression of this data.
Use the “Group number” column in the table to
represent the age group, the x-values. Graph the
regression equation on top of your scatter plot.

55. Example 11, continued
Age range 11–20 21–30 31–40 41–50 51–60 61–70
Group
number (x)
1 2 3 4 5 6
Number of
people who
exercise (y)
21 38 43 41 26 11

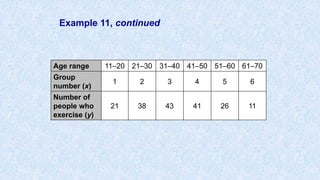
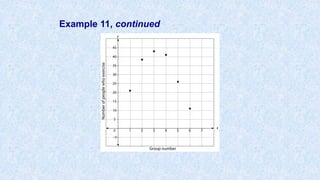
56. Example 11, continued
Make a scatter plot of the data.
On a TI-83/84:
Step 1: Press [STAT].
Step 2: Press [ENTER] to select Edit.
Step 3: Enter x-values into L1.
Step 4: Enter y-values into L2.
Step 5: Press [2nd][Y=].
Step 6: Press [ENTER] twice to turn on the Stat Plot.
Step 7: Press [ZOOM][9] to select ZoomStat and
show the scatter plot.

57. Example 11, continued

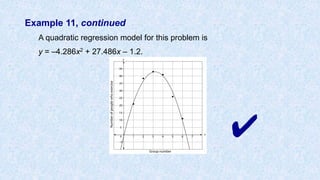
58. Example 11, continued
Find the quadratic regression model that best fits this
data.
On a TI-83/84:
Step 1: Press [STAT].
Step 2: Arrow to the right to select Calc.
Step 3: Press [5] to select QuadReg.
Step 4: At the QuadReg screen, enter the parameters for the
function (Xlist: L1, Ylist: L2, Store RegEQ: Y1). To enter Y1,
press [VARS] and arrow over to the right to “Y-VARS.”
Select 1: Function. Select 1: Y1.
Step 5: Press [ENTER] twice to see the quadratic regression
equation.
Step 6: Press [ZOOM][9] to view the graph of the scatter plot and
the regression equation.

59. Example 11, continued
A quadratic regression model for this problem is
y = –4.286x2 + 27.486x – 1.2.
✔

60. Example 12
Doctors recommend that most people exercise for 30
minutes every day to stay healthy. To get the best
results, a person’s heart rate while exercising should
reach between 50% and 75% of his or her maximum
heart rate, which is usually found by subtracting your
age from 220. The peak rate should occur at around the
25th minute of exercise. Alice is 30 years old, and her
maximum heart rate is 190 beats per minute (bpm).
Assume that her resting rate is 60 bpm.
60
5.9.2: Fitting a Function to Data

61. Example 12, continued
The table below shows Alice’s heart rate as it is
measured every 5 minutes for 30 minutes while she
exercises. Interpret the model.
Make a scatter plot of the data. Use a graphing
calculator to find a quadratic regression model for the
data. Use your model to extrapolate Alice’s heart rate
after 35 minutes of exercise.
Time (minutes) 0 5 10 15 20 25 30
Heart rate (bpm) 60 93 113 134 142 152 148

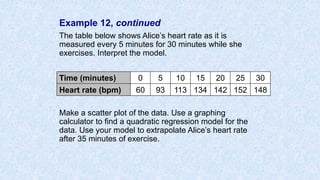
62. Example 12, continued
Make a scatter plot of the data.
On a TI-83/84:
Step 1: Press [STAT].
Step 2: Press [ENTER] to select Edit.
Step 3: Enter x-values into L1.
Step 4: Enter y-values into L2.
Step 5: Press [2nd][Y=].
Step 6: Press [ENTER] twice to turn on the Stat Plot.
Step 7: Press [ZOOM][9] to select ZoomStat and
show the scatter plot.

63. Example 12, continued

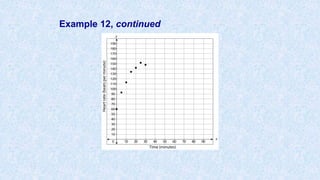
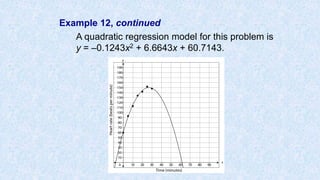
64. Example 12, continued
Find a quadratic regression model using your
graphing calculator.
On a TI-83/84:
Step 1: Press [STAT].
Step 2: Arrow to the right to select Calc.
Step 3: Press [5] to select QuadReg.
Step 4: At the QuadReg screen, enter the
parameters for the function (Xlist: L1, Ylist:
L2, Store RegEQ: Y1). To enter Y1, press
[VARS] and arrow over to the right to “Y-
VARS.” Select 1: Function. Select 1: Y1.
Step 5: Press [ENTER] twice to see the quadratic
regression equation.
Step 6: Press [ZOOM][9] to view the graph of the
scatter plot and the regression equation

65. Example 12, continued
A quadratic regression model for this problem is
y = –0.1243x2 + 6.6643x + 60.7143.

66. Example 12, continued
Use your model to extrapolate Alice’s heart
rate after 35 minutes of exercise.
Substitute 35 for x in the regression model.
y = –0.1243(35)2 + 6.6643(35) + 60.7143
y ≈ 141.70
After 35 minutes of exercise, we can expect Alice’s
heart rate to be approximately 141.7 beats per
minute.

67. Example 12, continued
Interpret the model.
Alice appears to be reducing her heart rate and,
therefore, reducing her exercise intensity after a peak
at approximately 27 minutes. If she continues the
trend, her heart rate will be back to her resting heart
rate at approximately 54 minutes. Heart rates below
her resting heart rate can be ignored.
✔