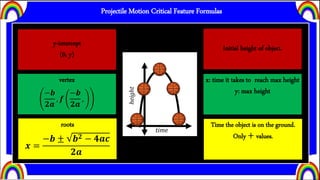
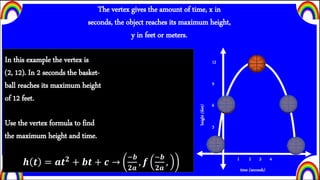
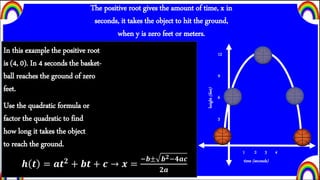
This document discusses key formulas and concepts for projectile motion: 1) It provides the quadratic formulas for calculating the height of an object over time whether thrown or dropped, in both feet and meters. 2) It defines critical features of projectile motion formulas like the y-intercept, vertex, and roots which relate to the initial height, maximum height and time, and time it takes the object to hit the ground. 3) Examples are given of applying these concepts and formulas to the motion of a basketball to determine its initial height, maximum height and time, and time to reach the ground.

1. Projectile Motion Formulas
f(x) = a𝒙 𝟐
+ bx + c
When objects are thrown.
feet:
𝒉 𝒕 = −𝟏𝟔𝒕 𝟐
+ 𝒗 𝟎 𝒕 + 𝒉 𝟎
When objects are dropped.
feet:
𝒉 𝒕 = −𝟏𝟔𝒕 𝟐 + 𝒉 𝟎
meters:
𝒉 𝒕 = −𝟒. 𝟗𝒕 𝟐
+ 𝒗 𝟎 𝒕 + 𝒉 𝟎
meters:
𝒉 𝒕 = −𝟒. 𝟗𝒕 𝟐
+ 𝒉 𝟎

2. Projectile Motion Critical Feature Formulas
roots
𝒙 =
−𝒃 ± 𝒃 𝟐 − 𝟒𝒂𝒄
𝟐𝒂
y-intercept
(0, y)
vertex
−𝒃
𝟐𝒂
, 𝒇
−𝒃
𝟐𝒂
,
Initial height of object.
x: time it takes to reach max height
y: max height
Time the object is on the ground.
Only + values.height time

3. 12
9
6
3
1 2 3 4
height(feet)
time (seconds)
The y-intercept is the height in which the
object begins. It is when x, seconds, is zero.
In this example the y-intercept
is (0, 6) The basketball begins
at 6 feet. This is the “c” value
of the quadratic equation.
𝒉 𝒕 = 𝒂𝒕 𝟐
+ 𝒃𝒕 + 𝒄
𝒉 𝒕 = 𝒂𝒕 𝟐
+ 𝒃𝒕 + 𝟔

4. 12
9
6
3
1 2 3 4
height(feet)
time (seconds)
The vertex gives the amount of time, x in
seconds, the object reaches its maximum height,
y in feet or meters.
In this example the vertex is
(2, 12). In 2 seconds the basket-
ball reaches its maximum height
of 12 feet.
Use the vertex formula to find
the maximum height and time.
𝒉 𝒕 = 𝒂𝒕 𝟐
+ 𝒃𝒕 + 𝒄 →
−𝒃
𝟐𝒂
, 𝒇
−𝒃
𝟐𝒂
,

5. 12
9
6
3
1 2 3 4
height(feet)
time (seconds)
The positive root gives the amount of time, x in
seconds, it takes the object to hit the ground,
when y is zero feet or meters.
In this example the positive root
is (4, 0). In 4 seconds the basket-
ball reaches the ground of zero
feet.
Use the quadratic formula or
factor the quadratic to find
how long it takes the object
to reach the ground.
𝒉 𝒕 = 𝒂𝒕 𝟐
+ 𝒃𝒕 + 𝒄 → 𝒙 =
−𝒃± 𝒃 𝟐−𝟒𝒂𝒄
𝟐𝒂