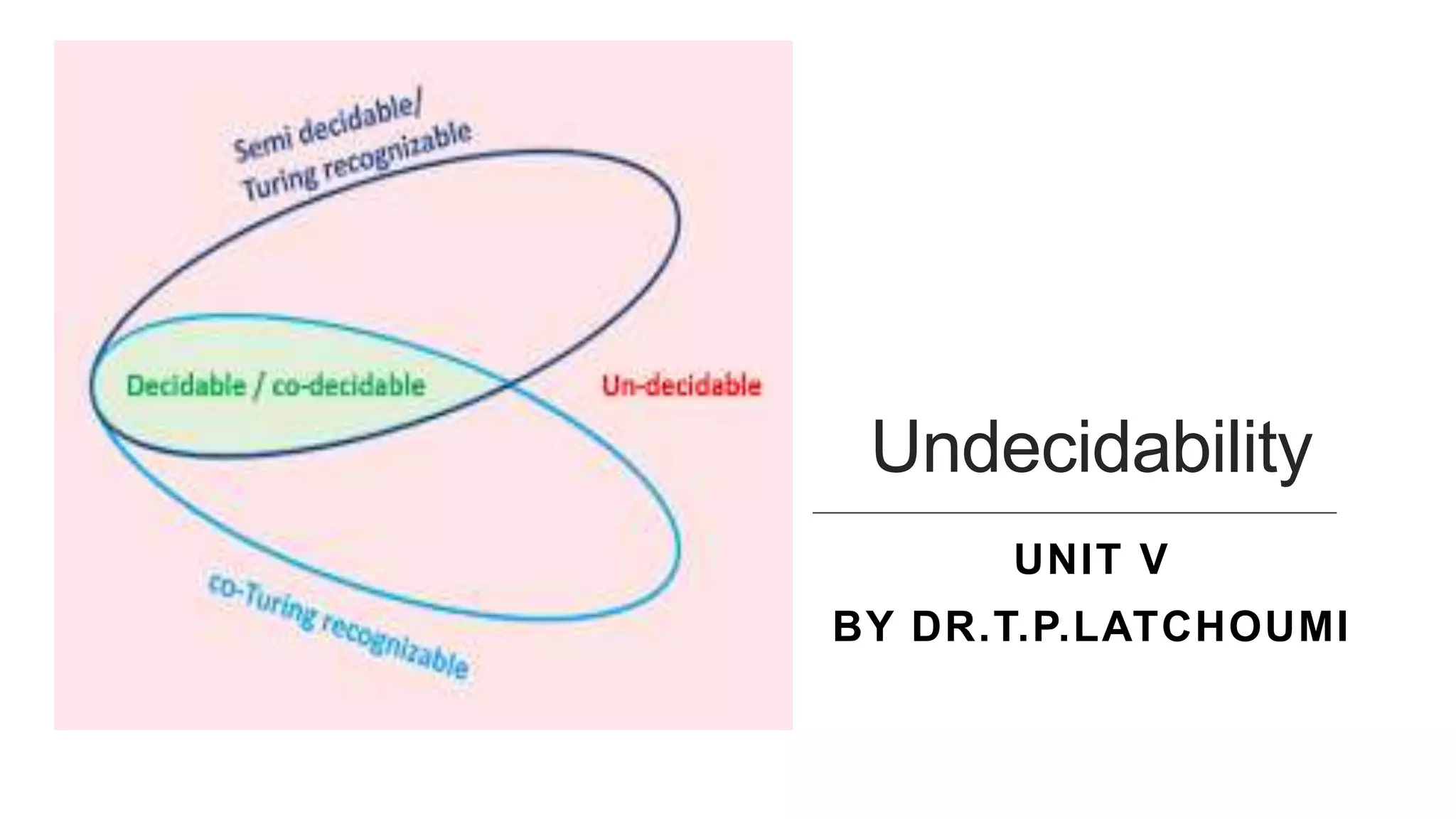
Undecidability refers to problems that cannot be solved algorithmically. Alan Turing first proved the existence of undecidable problems in 1936. There are decidable problems that can be solved by a Turing machine in finite time, and undecidable problems for which no Turing machine can provide a definitive yes or no answer. Examples of undecidable problems include determining if a context-free grammar is ambiguous or if two context-free languages are equal. Rice's theorem states that any non-trivial semantic property of a language recognized by a Turing machine is undecidable. Undecidability has important implications in language theory and for analyzing programs and computational problems.

1. Undecidability
UNIT V
BY DR.T.P.LATCHOUMI

2. Introduction
Alan Turing first proved this result in 1936. It is related to Gödel's Incompleteness Theorem,
which states that there is no system of logic strong enough to prove all true sentences of number
theory.
Essentially, Gödel uses a fix point construction to construct a self-referential sentence of number
theory which states something to the effect: "I am not provable".
The argument is quite complex. However, the argument is basically analogous to the one given
in support of the fact that the truth value of the statement ‘I am telling lies’ can not be determined.

3. Cont…
In view of the large number of applications of modern computer systems that help us in solving
problems from almost every domain of human experience, you might be tempted to think that
computers can solve any problem if the problem is properly formulated.
 We will prove that such problems cannot be solved no matter.
◦ What language is used?
◦ What machine is used?
◦ Much computational resources are devoted in attempting to solve the problem, etc.
For problems that cannot be solved by computational means, we can approximate their solutions,
but it's impossible to get the perfectly correct solutions in all cases.

4. Decidable
Problems
Examples
Equivalence of two regular languages: Given two
regular languages, there is an algorithm and a Turing
machine to decide whether two regular languages are
equal or not.
Finiteness of regular languages: Given a regular
language, there is an algorithm and a Turing machine to
decide whether regular language is finite or not.
Emptiness of context free languages: Given a context
free language, there is an algorithm whether CFL is
empty or not.
A problem is decidable if we can
construct a Turing machine which
will halt in finite amount of time for
every input and give an answer as
‘yes’ or ‘no’.
A decidable problem has an
algorithm to determine the answer
for a given input.

5. Example 1

6. Example 2

7. Example 3

8. Cont…

9. Undecidable
problems
Examples
The ambiguity of context-free languages: Given a context-
free language, there is no Turing machine which will always
halt in finite amount of time and give an answer whether
language is ambiguous or not.
Equivalence of two context-free languages: Given two
context-free languages, there is no Turing machine which will
always halt in finite amount of time and give an answer
whether two context free languages are equal or not.
A problem is undecidable if there
is no Turing machine which will
always halt in finite amount of time
to give an answer as ‘yes’ or ‘no’.
An undecidable problem has no
algorithm to determine the answer
for a given input.

10. Cont….
Everything or completeness of CFG: Given a CFG and
input alphabet, whether CFG will generate all possible
strings of the input alphabet (∑*) is undecidable.
Regularity of the CFL, CSL, REC and REC: Given a
CFL, CSL, REC or REC, determining whether this
language is regular is undecidable.

11. Semi-decidable Problems
A semi-decidable problem is a subset of undecidable
problems for which Turing machine will always halt in
finite amount of time to answer as ‘yes’ and may or may not
halt for an answer as ‘no’.

12. Example
 Are two regular languages L and M equivalent?
We can easily check this by using Set Difference
operation.
L-M =Null and M-L =Null.
Hence (L-M) U (M-L) = Null, then L, M is equivalent.
 Membership of a CFL?
We can always find whether a string exists in a given
CFL by using on algorithms based on dynamic
programming.
 Emptiness of a CFL
By checking the production rules of the CFL we can
easily state whether the language generates any strings or
not.
We will now consider few
important Decidable problems:

13. The relationship between semi-decidable,
undecidable and decidable problem

14. Definitions
A language is called Decidable or
Recursive if there is a Turing
machine which accepts and halts on
every input string w.
Every decidable language is Turing-
Acceptable.
A decision problem P is decidable if the language L of all yes,
instances to P is decidable.

15. For a decidable language, for each
input string, the TM halts either at
the accept or the reject state as
depicted in the following diagram –

16. Example 1
Solution
Prime numbers = {2, 3, 5, 7, 11, 13, …………..}
Divide the number ‘m’ by all the numbers between ‘2’
and ‘√m’ starting from ‘2’.
If any of these numbers produce a remainder zero, then it
goes to the “Rejected state”, otherwise it goes to the
“Accepted state”. So, here the answer could be made by
‘Yes’ or ‘No’.
Hence, it is a decidable problem.
Find out whether the following
problem is decidable or not − Is a
number ‘m’ prime?

17. Example 2
Solution
Take the DFA that accepts L and check if w is accepted
Given a regular language L and
string w, how can we check if w ∈
L?

18. A Language that is not
Recursively
Enumerable (RE)
RE languages or type-0 languages are generated by
type-0 grammars.
A RE language can be accepted or recognized by Turing
machine which means it will enter into a final state for
the strings of language and may or may not enter into
rejecting state for the strings which are not part of the
language.
It means TM can loop forever for the strings which are
not a part of the language.
RE languages are also called as Turing recognizable
languages
Recursive Enumerable (RE) or
Type -0 Language

19. Definition
The language L is called a recursive enumerable
languages, if and only if each and every string which
belongs to L is either accepted by a Turing machine and
rejects or loops forever every other string which does not
belong to L.
In other words, we can say recursively enumerable (re)
languages are accepted by TM.

20. Recursive
Language (REC)
A recursive language (subset of RE) can be decided by
Turing machine which means it will enter into a final
state for the strings of language and rejecting state for the
strings which are not part of the language.
E.g.; L= {anbncn|n>=1} is recursive because we can
construct a Turing machine which will move to final
state if the string is of the form anbncn else move to non-
final state.
So the TM will always halt in this case. REC languages
are also called as Turing decidable languages.

21. Definition
Recursive Language = accepts L and rejects L’
Recursive Enumerable language= accepts L and rejects
or loops for L’.
The relationship between RE and REC languages can be
shown in Figure.
A language L is recursive if there is a
Turing machine that recognizers L.
The recursively enumerable
languages are called Turing-
acceptable and recursive languages
are called Turing-decidable
respectively.
Let L be any language accepted by
TM and L’ be the complement of L.

22. Types of TM

23. Properties of Recursive
and Recursively
enumerable language
Theorem 1:
If the language L is a recursive language, then the complement of
L’ is also a recursive language. That is recursive language are
closed under complementation.
Proof:
Let M be a TM which accepts the input w and enters into the
accept halt state.
Construct M’ such that if M enters in halt state without accepting w
then M’ enters in the halt state by accepting the same w.
A language is recursive if at least
one Turing machine exits which
accepts it and rejects its
complement.
There is no loop forever set existing
in TM for recursive languages.

24. Theorem 2
Proof:
Let L1 and L2 be the two recursive languages is recursive and union of two
recursively enumerable languages is also a recursively enumerable language.
We construct M, which first simulates M1.
If M1 accepts, then M accepts, if M1 rejects, then M simulates M2 and accepts if
and only if M2 accepts.
Since both M1 and M2 are algorithms, M is definitely going to halt.
Thus M accepts L1UL2.
The union of two recursive
languages is recursive and union of
two recursively enumerable
languages is also a recursively
enumerable language.
a. Construction of recursive languages.
b. Construction of recursively enumerable
languages

25. Theorem 3
Proof:
Let L and L’ are the languages accepted by M1 and M2
respectively.
Simulate M1 and M2 simultaneously M accepts w if M1
accepts w and rejects w if M2 accepts w.
If language L and its complement L’
both are recursively enumerable,
then L and L’ are recursive.

26. Example 1

27. Cont….

28. Example 2

29. Cont…

30. Theorem

31. Cont…

32. Cont…

33. An Undecidable
problem that is
RE
We have already shown that it is
undecidable whether a context-free
grammar is ambiguous.
The proof technique we used was to
reduce Post’s Correspondence
Problem to the ambiguity problem for
CFG’s.
We can also use this proof technique
to show a number of important
problems about context-free
languages are undecidable.

34. Cont…
Proof of the undecidability of the
validity problem for the set of
sentences written as a formal-exists
quantifier alternation applied to
positive word equations.
A corollary of this undecidability
result is that this set is undecidable
even with sentences with at most
two occurrences of a string variable.

35. Undecidable
problems about
Turing Machine
Examples of undecidable problems
• About Turing machines:
Is the language accepted by a TM empty, finite, regular, or
context-free?
Does a TM meet its “specification ? ,” that is, does it have
any “bugs.”
One may ask, Why is this important? A reduction of
problem B to problem A shows that problem A is at least as
difficult to solve as problem B.
Also, we can show the following:
• To show that a problem A is undecidable, we reduce
another problem that is known to be undecidable to A.
• Having proved that the halting problem is undecidable, we
use problem reduction to show that other problems are
undecidable.
Once we have shown that the
halting problem is undecidable, we
can show that a large class of other
problems about the input/output
behavior of programs is
undecidable.

36. Example 1:
Totality
Problem
Proof: We prove that the halting problem is reducible to
the totality problem. That is, if an algorithm can solve the
totality problem, it can be used to solve the halting
problem. Since no algorithm can solve the halting
problem, the totality problem must also be undecidable.
The reduction is as follows. For any TM M and input w,
we create another TM M1 that takes an arbitrary input,
ignores it, and runs M on w.
Note that M1 halts at all inputs if and only if M halts on
input w. Therefore, an algorithm that tells us whether M1
halts on all inputs also tells us whether M halts on input
w, which would be a solution to the halting problem.
Hence, The totality problem is undecidable.
Decide whether an arbitrary TM
halts on all inputs. (If it does, it
computes a “total function”).
This is equivalent to the problem of
whether a program can ever enter
an infinite loop, for any input.
It differs from the halting problem,
which asks whether it enters an
infinite loop for a particular input.

37. Example 2:
Equivalence
problem
Proof: We prove that the totality problem is reducible to
the equivalence problem. That is, if an algorithm can
solve the equivalence problem, it can be used to solve
the totality problem. Since no algorithm can solve the
totality problem, the equivalence problem must also be
unsolvable.
The reduction is as follows. For any TM M, we can
construct a TM M1 that takes any input w, runs M on that
input, and outputs “yes” if M halts on w.
We can also construct a TM M2 that takes any input and
simply outputs “yes.” If an algorithm can tell us whether
M1 and M2 are equivalent, it can also tell us whether M1
halts on all inputs, which would be a solution to the
totality problem.
Hence, the equivalence problem is undecidable.
Decide whether two TMs accept the
same language.
This is equivalent to the problem of
whether two programs compute the
same output for every input.

38. Post’s
Correspondence
Problem
Let Σ be an alphabet, and let L and M be two lists of
nonempty strings over Σ, such that L and M have the
same number of strings. We can represent L and M as
follows.
Undecidable problems arise in
language theory also. It is required
to develop techniques for proving
particular problems undecidable.
In 1946, Emil Post proved that the
following problem is undecidable:

39. Example 1

40. Example 2

41. Example 3
Consider the following instance of the PCP:
Alphabet Σ = { a, b }
List L = (a, ab)
List M = (aa, b)
We see that ( 1, 2 ) is a sequence of integers that solves
this PCP instance, since the concatenation of a and ab is
equal to the concatenation of aa and b (i.e w1 w2 = v1 v2
= aab). other solutions include: ( 1, 2, 1, 2 ) , ( 1, 2, 1, 2,
1, 2 ) and so on.

42. Example 4
Solution:
A solution is 2, 1, 1, 3. That means w2w1w1w3 = x2x1x1x3
The constructed string from both lists is bab3b3a.
Consider the correspondence
system as given below
A = (b, bab3, ba) and B = (b3, ba, a).
The input set is ∑ = {0, 1}. Find the
solution.

43. Rice Theorem
Formal Definition
If P is a non-trivial property, and the language holding
the property, Lp , is recognized by Turing machine M,
then Lp = {<M> | L(M) ∈ P} is undecidable.
Rice theorem states that any non-
trivial semantic property of a
language which is recognized by a
Turing machine is undecidable.
A property, P, is the language of all
Turing machines that satisfy that
property.

44. Description and
Properties
Property of languages, P, is simply a set of languages. If
any language belongs to P (L ∈ P), it is said that L satisfies
the property P.
A property is called to be trivial if either it is not satisfied
by any recursively enumerable languages, or if it is satisfied
by all recursively enumerable languages.
A non-trivial property is satisfied by some recursively
enumerable languages and are not satisfied by others.
Formally speaking, in a non-trivial property, where L ∈ P,
both the following properties hold:
◦ Property 1 − There exists Turing Machines, M1 and M2 that
recognize the same language, i.e. either ( <M1>, <M2> ∈ L ) or
( <M1>,<M2> ∉ L )
◦ Property 2 − There exists Turing Machines M1 and M2, where
M1 recognizes the language while M2 does not, i.e. <M1> ∈ L
and <M2> ∉ L

45. Theorem

46. Cont…

47. Rice theorem
for some
undecidable
languages
Any non-trivial property of the
language recognizable by a Turing
machine (recursively enumerable
language) is undecidable.

48. Rice theorem for some
unrecognizable
language
Any non-monotonic property of the
language recognizable by a Turing
machine (recursively enumerable
language) is unrecognizable

49. Cont…

50. Cont….

51. Applications of
Rice’s Theorem
From Rice’s theorem, we can conclude that a whole host
of TM-related problems are undecidable, including:
Is L(M)L(M) a regular language?
Is L(M)L(M) a CFL?
Is L(M)L(M) empty?
Does L(M)L(M) include any palindromes?