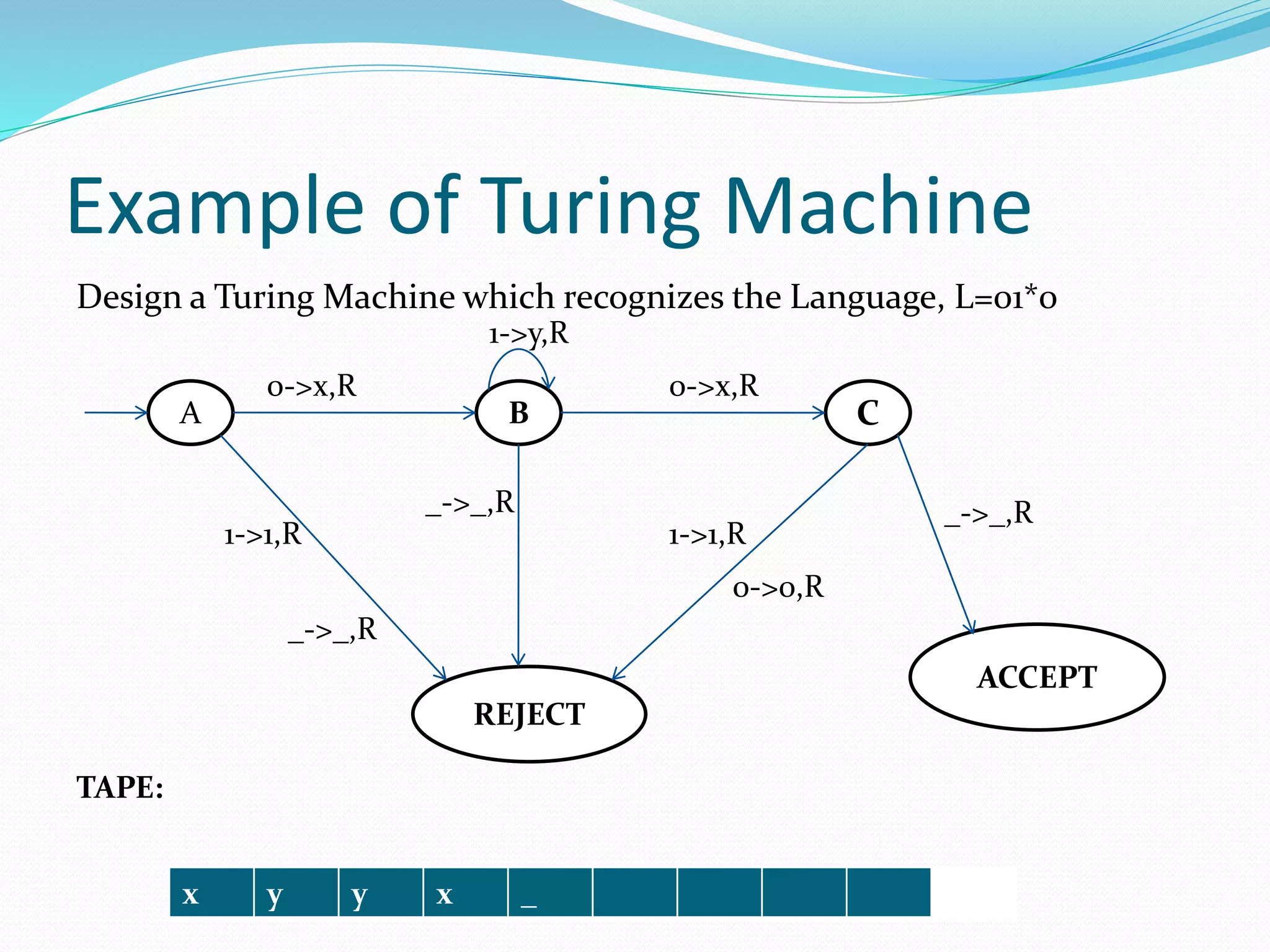
The document provides an overview of Turing machines, detailing their components, operational principles, and properties such as recognizability and decidability. It discusses the implications of the halting problem, modifications of Turing machines, and their applications in demonstrating computational completeness. Ultimately, it emphasizes the significance of Turing machines in computer science as a model for all computable problems.

1. Theory of Automata
By: Muhammad Samran Tanveer

2. Contents
1. INTRODUCTION
2. Turing Machine MODEL
3. FORMAL DEFINITION
4. WORKING WITH EXAMPLE
5. PROPERTIES
6. MODIFICATIONS
7. THE HALTING PROBLEM
8. ADVANTAGES
9. POWER OF TM
10. APPLICATION

3. What is Turing Machine?
o Consists of an infinite tape (as the memory)
o A tape head (a pointer to the currently
inspected cell of the memory)
o And a state transition table(to govern the
behavior of the machine)

4. Introduction to Turing Machine
o Invented by esteemed computer scientist ALAN
TURING in 1936
o Basically an abstract computational model that
performs computations
o Provide a powerful computational model for solving
problems in computer science
o Capable of simulating common computers

5. The Turing Machine Model

6. Definition
A Turing Machine is a seven-tuple:
M = (Q, Σ, Γ, δ, q0, B, F)
Q -> A finite set of states
Σ -> A finite input alphabet set
Γ -> A finite tape alphabet
B -> A distinguished blank symbol, which is in Γ
q0 -> The initial/starting state, q0 is inQ
F -> A set of final/accepting states, which is a subset ofQ
δ -> A Transition function,
Intuitively, δ(q,s) specifies the next state, symbol to be written, and
the direction of tape head movement by M after reading symbol s
while in state q.

7. How it Works
The machine operates on an infinite memory
tape divided into discrete cells. The machine
positions its head over a cell and reads the
symbol there.
Then, as per the symbol and its present place
in user specified instructions , the machine
1. Writes a symbol in the cell, then
2. Either moves the tape one cell right or left
3. Either proceeds to a subsequent instruction
or halts the computation.

8. Example of Turing Machine
Design a Turing Machine which recognizes the Language, L=01*0
A B C
REJECT
ACCEPT
0->x,R
1->y,R
0->x,R
1->1,R
0->0,R
_->_,R
1->1,R
_->_,R
_->_,R
x y y x _
TAPE:

9. Properties of Turing Machine
o Recognisability : A language is recognizable if a TM
accepts when an input string is in the language, and
either rejects or loops forever when an input string is not
in the language.
o Decidability : A language is decidable if a TM accepts
strings that are in the language and rejects that are not
in the language. That is, TM will halt on all inputs.
o The Halting Problem is recognizable but
undecidable.

10. Modifications in Turing Machine
o Multi– tape TM
o Multi –track TM
o Non– deterministic TM
o TM with semi—infinite tape
These all give same performance as the standard TM
gives.

11. Block Diagram of Halting Machine

12. Inverted Halting Machine
o Now we will design an inverted halting machine
(HM) as −
o If H returns YES, then loop forever.
o If H returns NO, then halt.
o Further, a machine (HM)2 which input itself is
constructed as follows −
o If (HM)2 halts on input, loop forever.
o Else, halt.
o Here, we have got a contradiction. Hence, the
halting problem is undecidable.

13. Following is the Block Diagram of
Inverted Halting Machine

14. Advantages of Turing Machine
o Turing Machines are similar to finite automata/finite
state machines but have the advantage of unlimited
memory.
o They are capable of simulating common computers; a
problem that a common computer can solve (given
enough memory) will also be solvable using a Turing
machine, and vice versa.
o Simplicity of proofs
As a theoretic model, Turing machines have the charm
of being "simple" in the sense that the current machine
state has only constant size. All the information you
need in order to determine the next machine state
is one symbol and one (control) state number. The
change to the machine state is equally small, adding
only the movement of the machine head.

15. Advantages of Turing Machine
o If you're designing some kind of programming
language (or anything else that is meant to
compute things), then you may want to ensure
that it is Turing-complete (i.e., capable of
computing anything that is computable) by
implementing a Turing machine in it.

16. Is Turing Machine Infinite or Just
Limited?
o At this point we could fall to arguing the impossibility
of the Turing machine because its tape can’t be
infinitely long.
o The machine doesn't, in fact, need an infinite tape,
just one that isn't limited in length and this is a
subtle difference.
o Imagine if you will that Turing machines are
produced with a very long but finite tape and if the
machine ever runs out of space you can just order
some more tape. This is the difference between the
tape actually being infinitely long or just unlimited…

17. Applications of Turing Machine
o The Church-Turing Thesis claims that any computable
problem can be computed by a Turing machine. This means
that a computer more powerful than a Turing machine is not
necessary to solve computable problems. The idea of Turing
completeness is closely related to this. A system is Turing
complete if it can compute every Turing computable function.
A programming language that is Turing complete is
theoretically capable of expressing all tasks accomplishable
by computers; nearly all programming languages are Turing
complete.
o To prove that something is Turing complete, it is sufficient to
show that it can simulate some other Turing complete system.
Usually, it is easiest to show that a system can simulate a
UNIVERSAL TURING MACHINE. A universal Turing machine
is a Turing machine that can simulate any other Turing
machine.

18. Conclusion
o You could say that the computer was invented twice–once by Charles
Babbage and once by Alan Turing.
o While Babbage’s machine was a practical thing but Turing’s was
just a machine of mind.
o Turing Machine is a model of what is physically computable.
o Turing Machine might take a little longer to work out on a
problem than the latest PC , but it will give the same result.
o If you have a system that can compute something
then a Turing Machine can compute it as well.
o What is more so far no system has been found that can goes
beyond a Turing Machine.

19. THANK YOU !