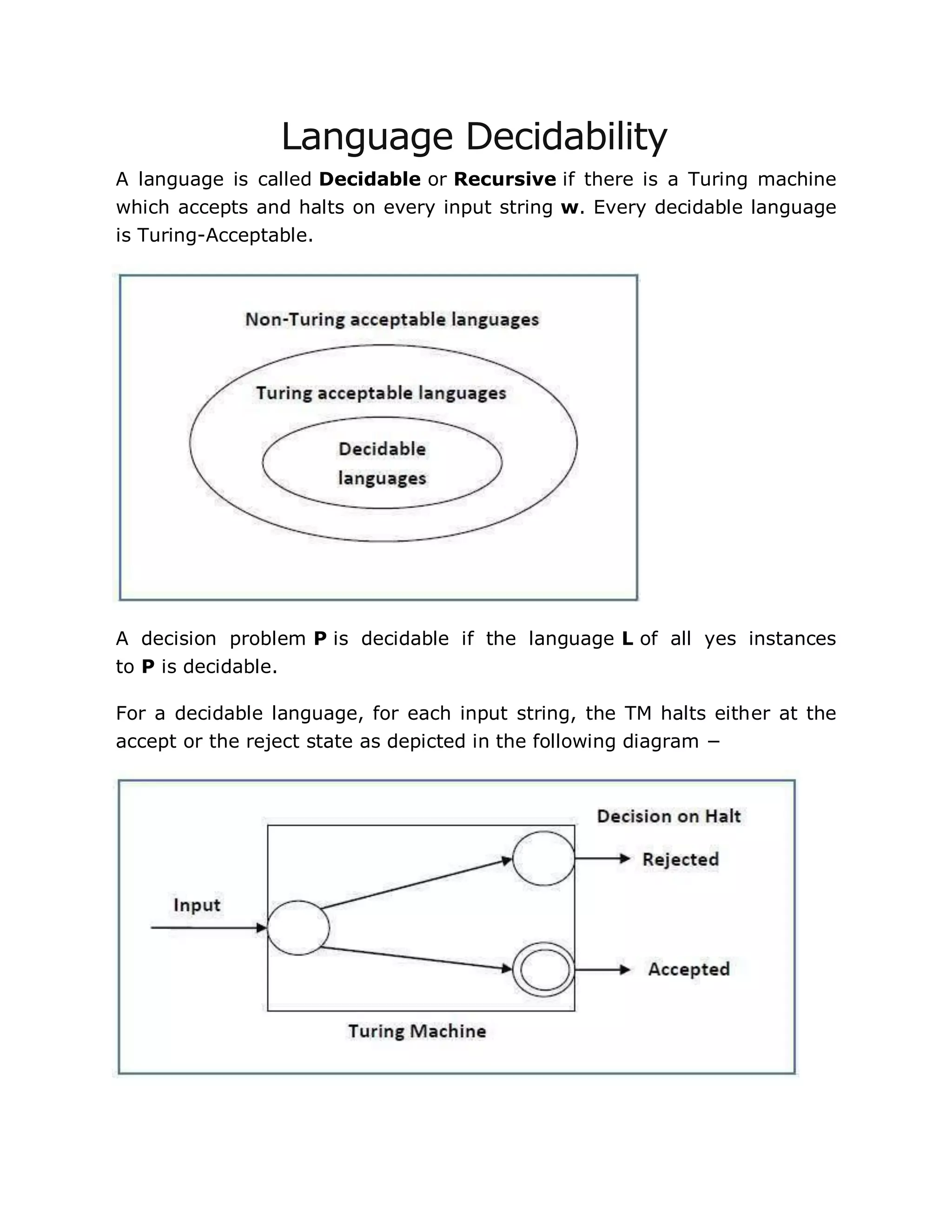
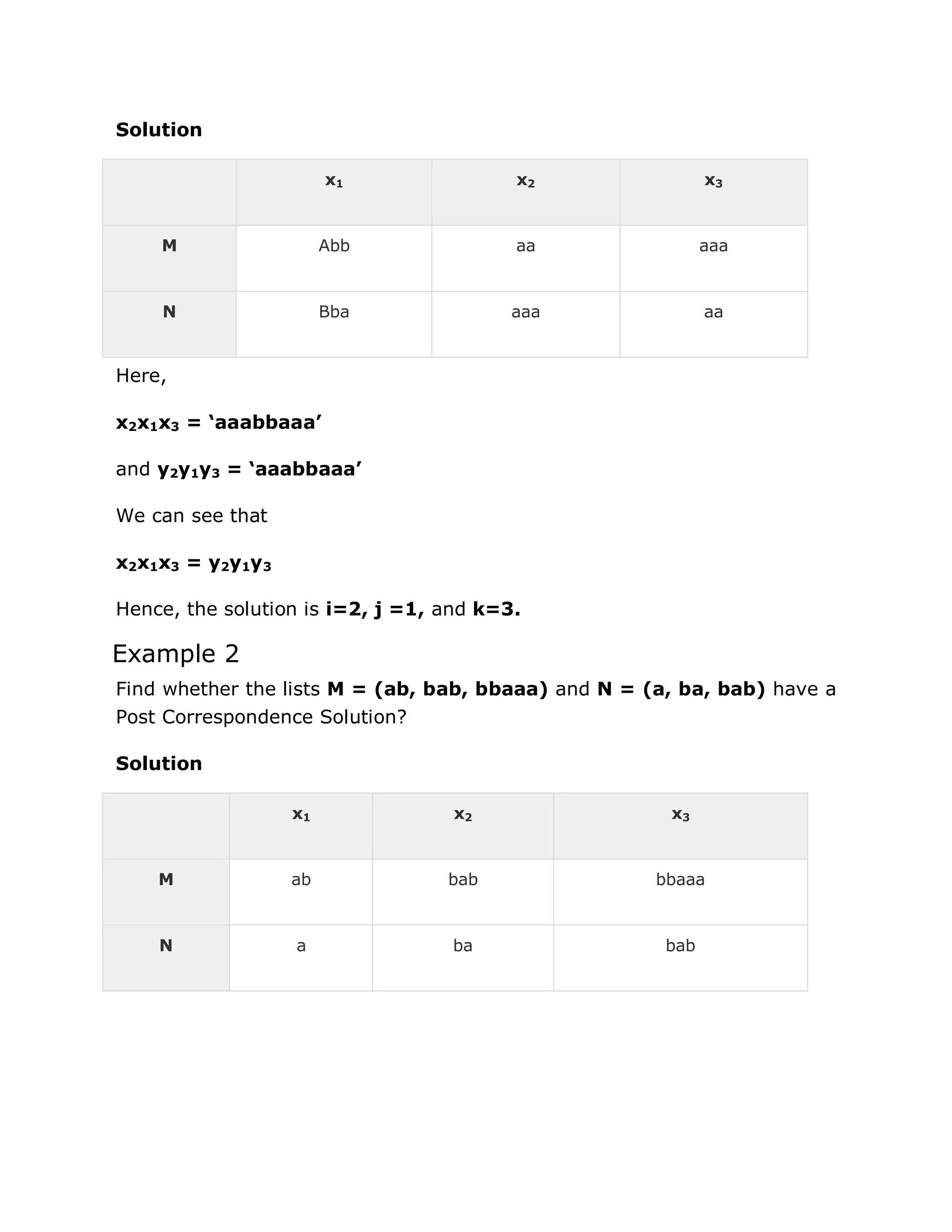
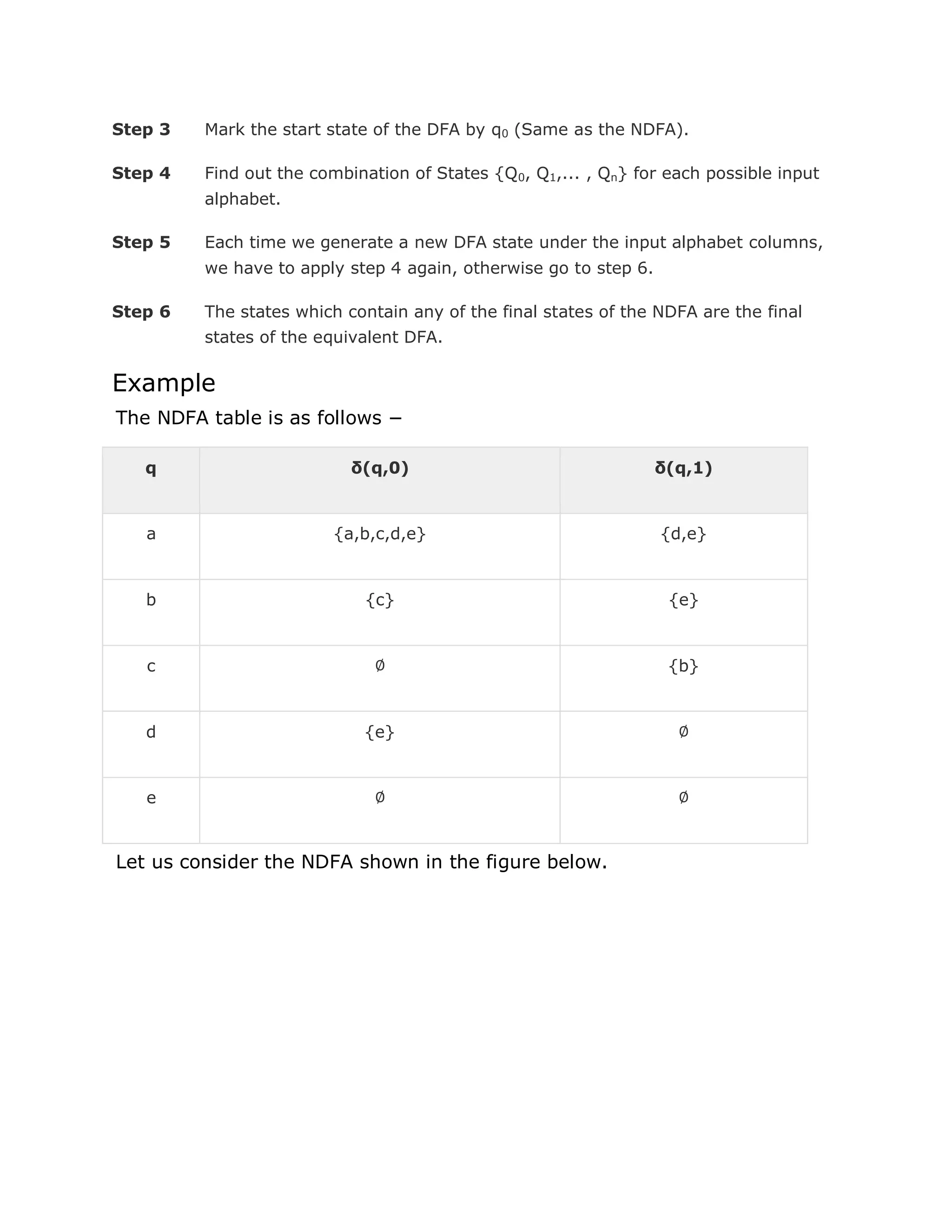
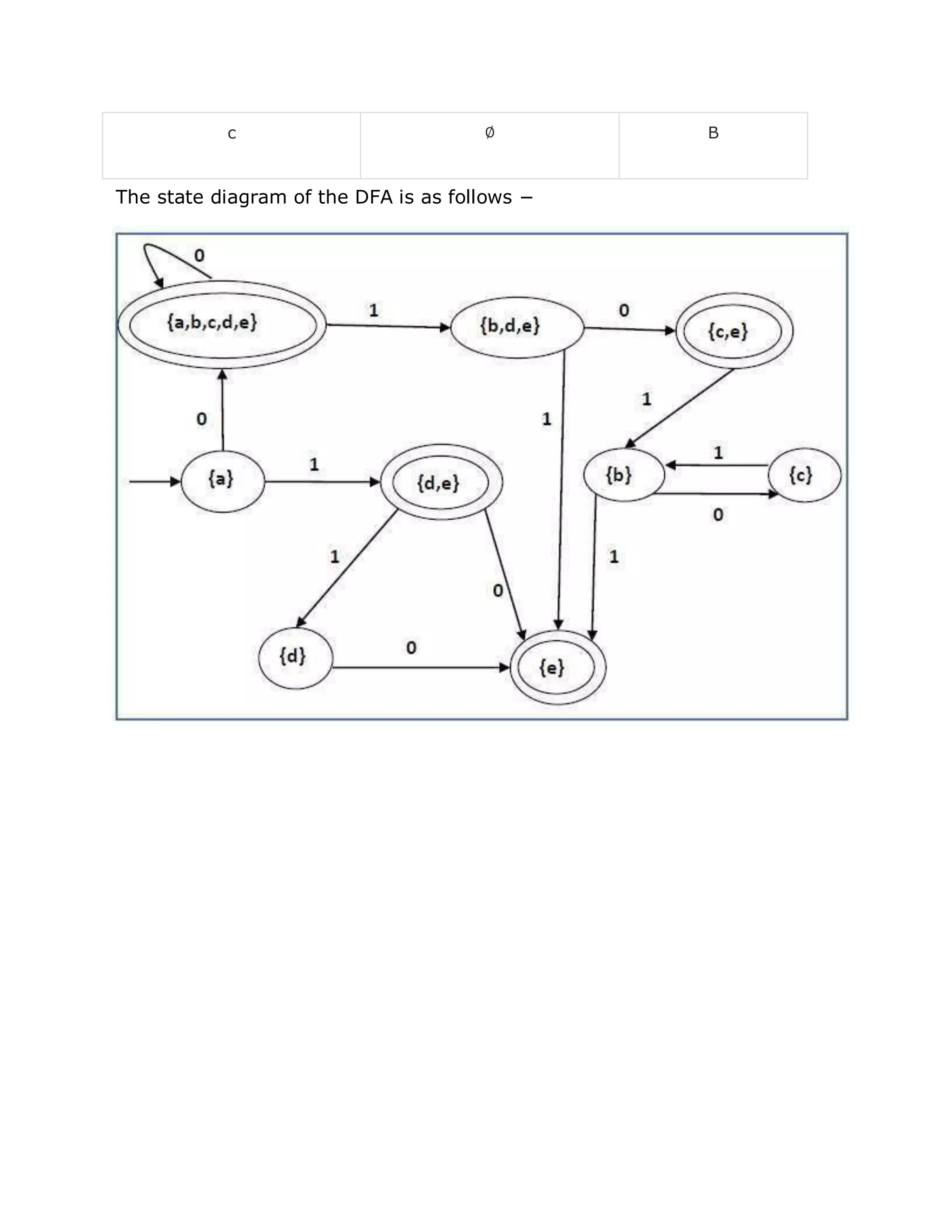
This document provides an introduction to automata theory and finite automata. It defines an automaton as an abstract computing device that follows a predetermined sequence of operations automatically. A finite automaton has a finite number of states and can be deterministic or non-deterministic. The document outlines the formal definitions and representations of finite automata. It also discusses related concepts like alphabets, strings, languages, and the conversions between non-deterministic and deterministic finite automata. Methods for minimizing deterministic finite automata using Myhill-Nerode theorem and equivalence theorem are also introduced.









![DFA Minimization
DFA Minimization using Myphill-Nerode
Theorem
Algorithm
Input: DFA
Output: Minimized DFA
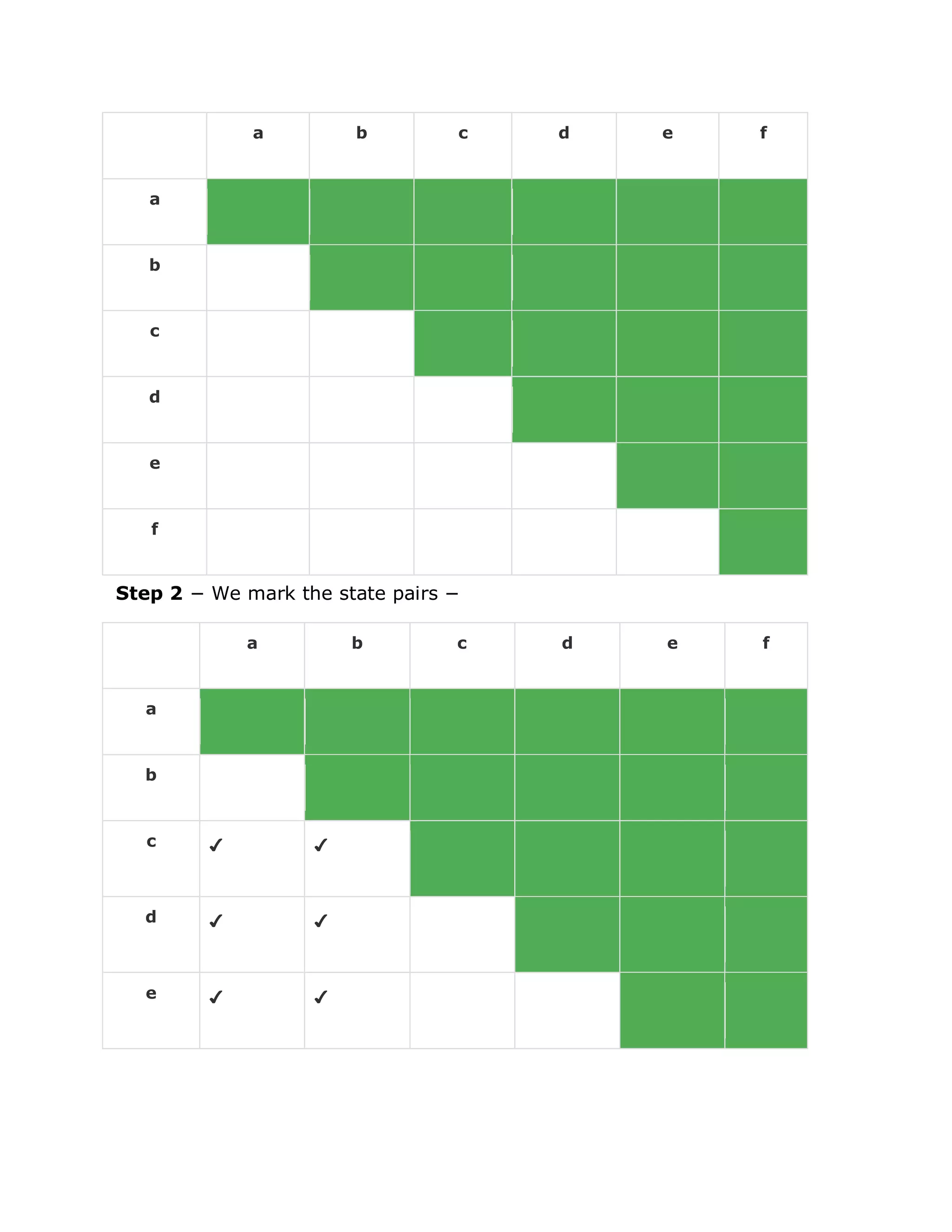
Step 1 Draw a table for all pairs of states (Qi, Qj) not necessarily connected directly
[All are unmarked initially]
Step 2 Consider every state pair (Qi, Qj) in the DFA where Qi ∈ F and Qj ∉ F or vice
versa and mark them. [Here F is the set of final states].
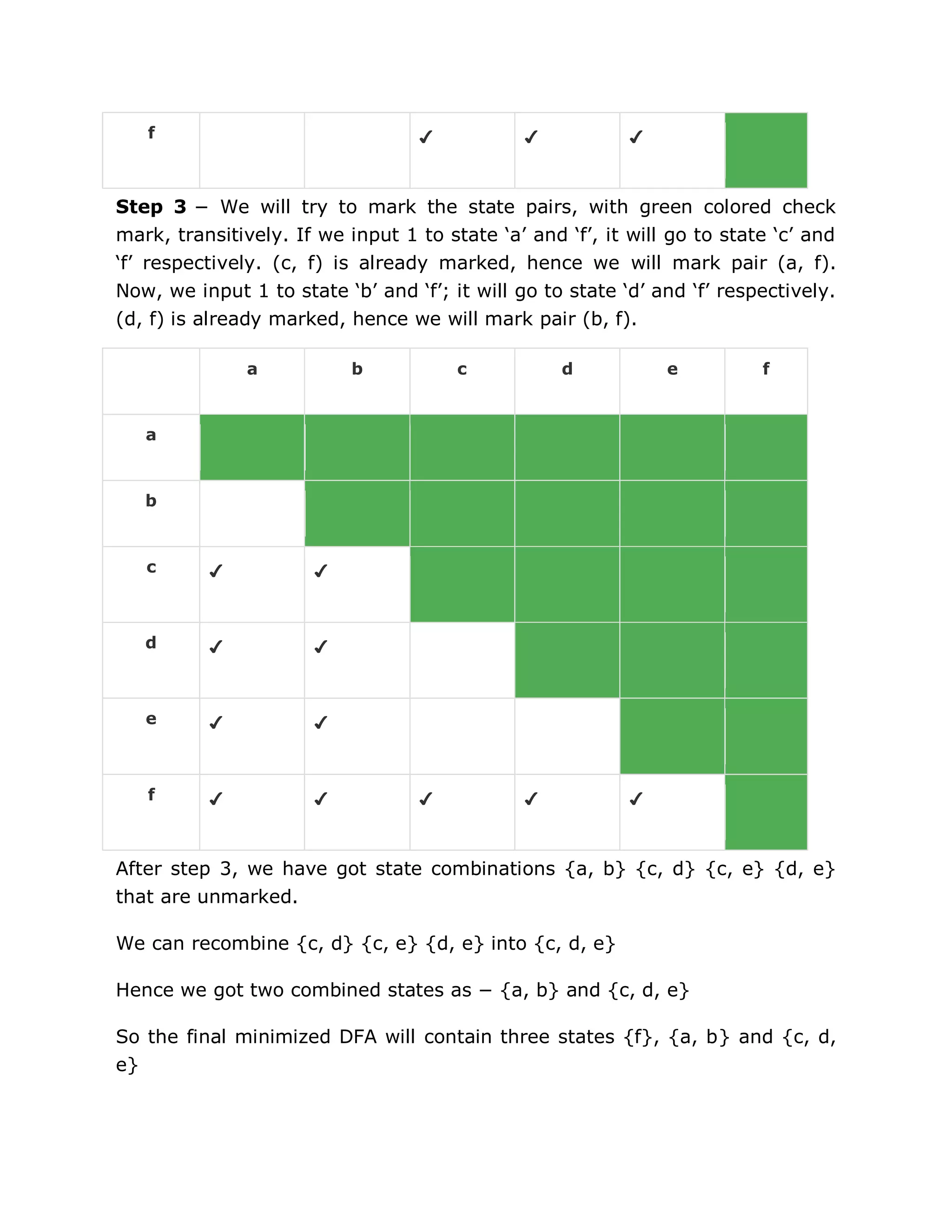
Step 3 Repeat this step until we cannot mark anymore states −
If there is an unmarked pair (Qi, Qj), mark it if the pair {δ(Qi, A), δ (Qi, A)}
is marked for some input alphabet.
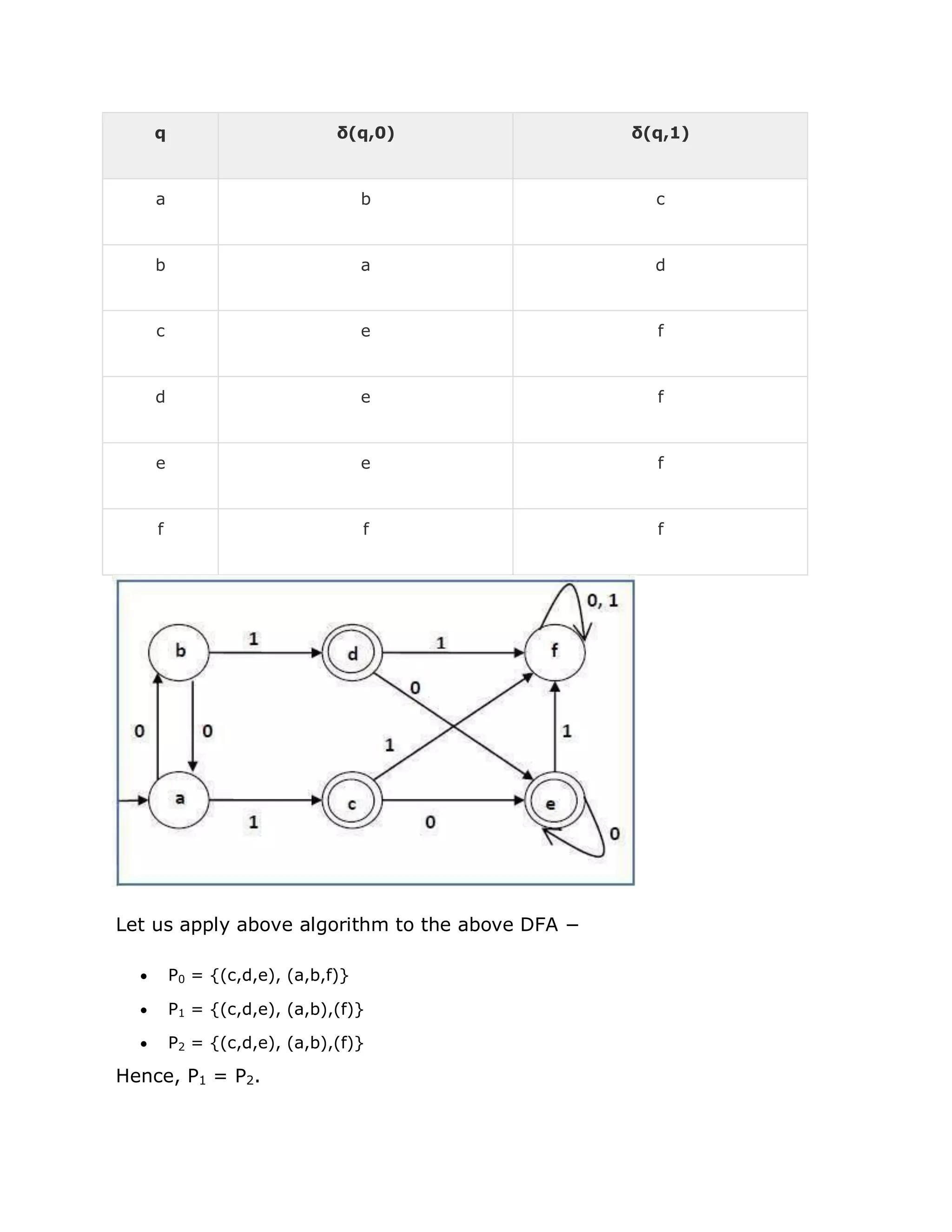
Step 4 Combine all the unmarked pair (Qi, Qj) and make them a single state in the
reduced DFA.
Example
Let us use above algorithm to minimize the DFA shown below.
Step 1 − We draw a table for all pair of states.](https://image.slidesharecdn.com/automatatheory-151106083026-lva1-app6891/75/Automata-theory-12-2048.jpg)



















![ (R*
)*
= R*
RR*
= R*R
(PQ)*P =P(QP)*
(a + b)*
= (a*
b*
)*
= (a*
+ b*
)*
= (a + b*
)*
= a*
(ba*
)*
R + ∅ = ∅ + R = R (The identity for union)
R ε = ε R = R (The identity for concatenation)
∅ L = L ∅ = ∅ (The annihilator for concatenation)
R + R = R (Idempotent law)
L (M + N) = LM + LN (Left distributive law)
(M + N) L = LM + LN (Right distributive law)
ε + RR*
= ε + R*R = R*
Arden's Theorem
In order to find out a regular expression of a Finite Automaton, we use
Arden‟s Theorem along with the properties of regular expressions.
Statement −
Let P and Q be two regular expressions.
If P does not contain null string, then R = Q + RP has a unique solution
that is R = QP*
Proof −
R = Q + (Q + RP)P [After putting the value R = Q + RP]
= Q + QP + RPP
When we put the value of R recursively again and again, we get the
following equation −
R = Q + QP
+ QP2
+ QP3
…..
R = Q (ε + P + P2
+ P3
+ …. )](https://image.slidesharecdn.com/automatatheory-151106083026-lva1-app6891/75/Automata-theory-37-2048.jpg)
![R = QP*
[As P* represents (ε + P + P2
+ P3
+ ….) ]
Hence, proved.
Assumptions for Applying Arden‟s Theorem −
The transition diagram must not have NULL transitions
It must have only one initial state
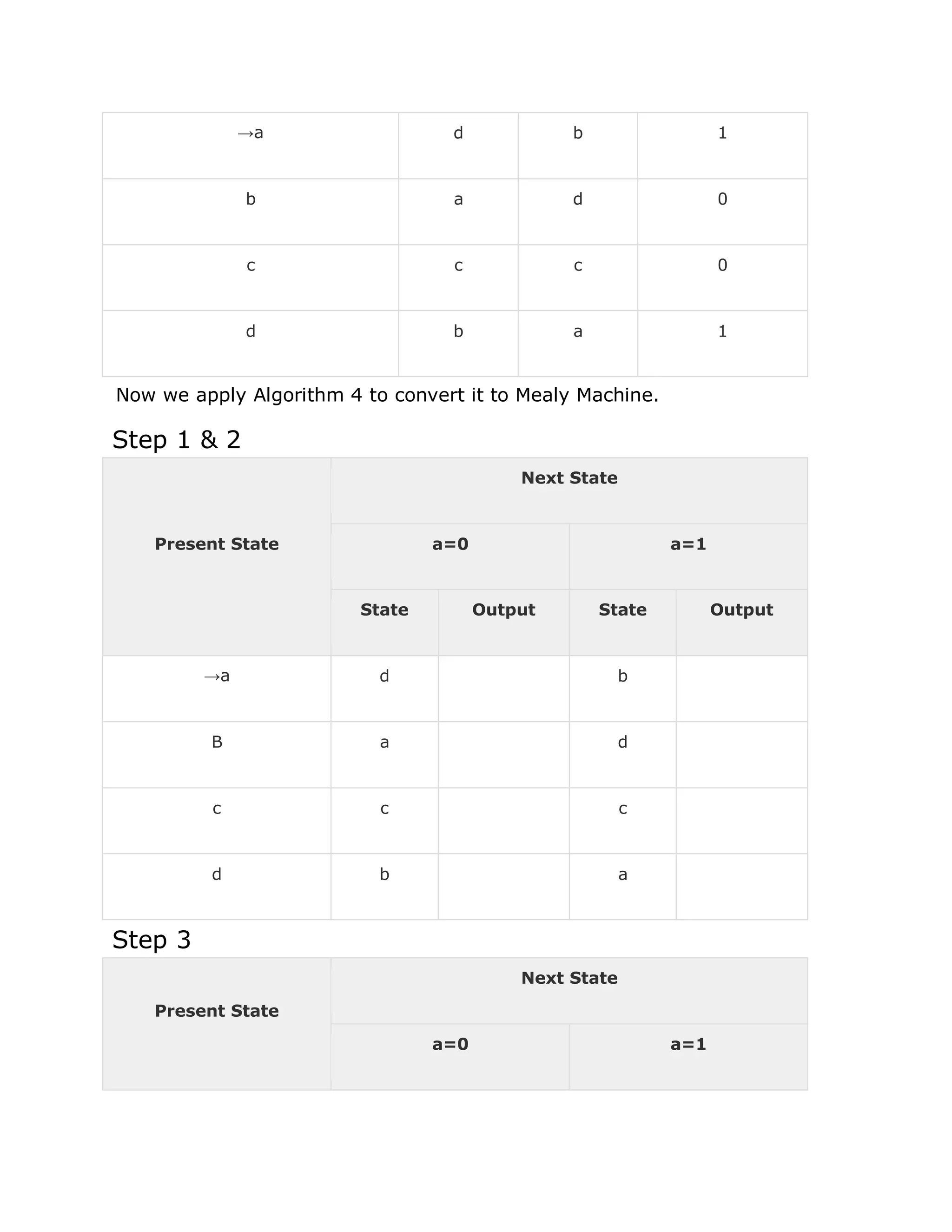
Method
Step 1 − Create equations as the following form for all the states of the
DFA having n states with initial state q1.
q1 = q1R11 + q2R21 + … + qnRn1 + ε
q2 = q1R12 + q2R22 + … + qnRn2
…………………………
……………………………
qn = q1R1n + q2R2n + … + qnRnn
Rij represents the set of labels of edges from qi to qj, if no such edge
exists, then Rij = ∅
Step 2 − Solve these equations to get the equation for the final state in
terms of Rij
Problem
Construct a regular expression corresponding to the automata given below
−](https://image.slidesharecdn.com/automatatheory-151106083026-lva1-app6891/75/Automata-theory-38-2048.jpg)
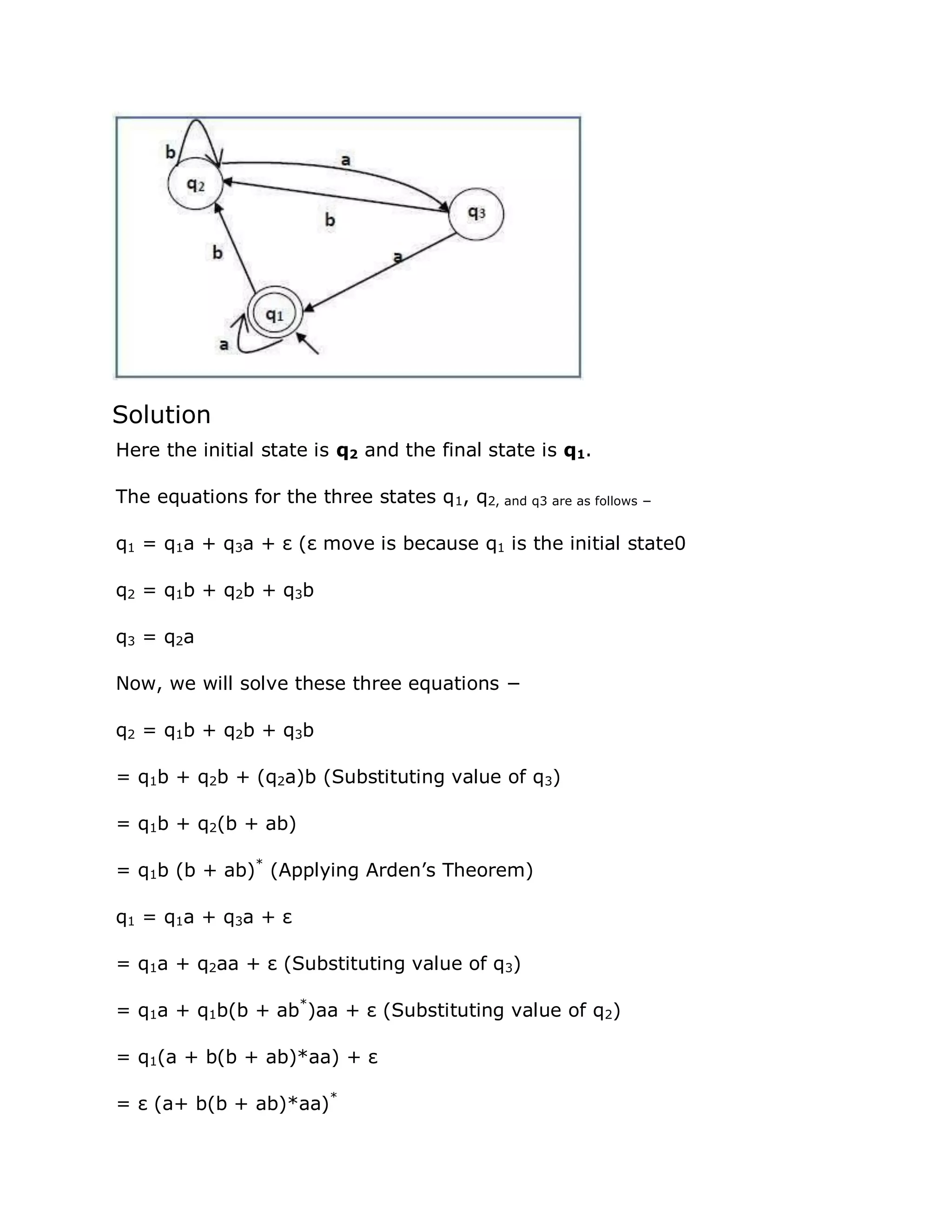
![= (a + b(b + ab)*aa)*
Hence, the regular expression is (a + b(b + ab)*aa)*
.
Problem
Construct a regular expression corresponding to the automata given below−
Solution
Here the initial state is q1 and the final state is q2
Now we write down the equations −
q1 = q10 + ε
q2 = q11 + q20
q3 = q21 + q30 + q31
Now, we will solve these three equations −
q1 = ε0*
[As, εR = R]
So, q1 = 0*
q2 = 0*1 + q20
So, q2 = 0*1(0)*
[By Arden‟s theorem]](https://image.slidesharecdn.com/automatatheory-151106083026-lva1-app6891/75/Automata-theory-40-2048.jpg)







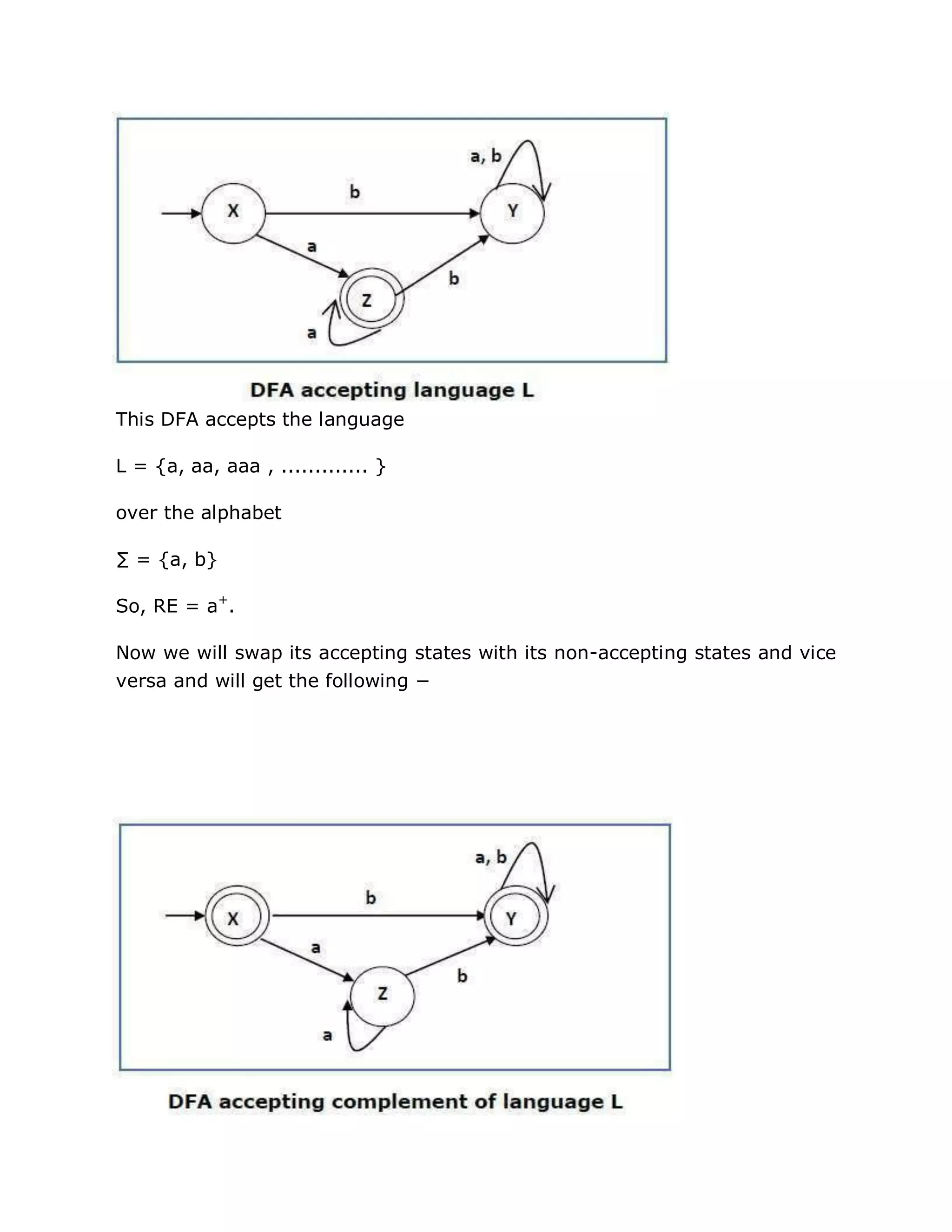





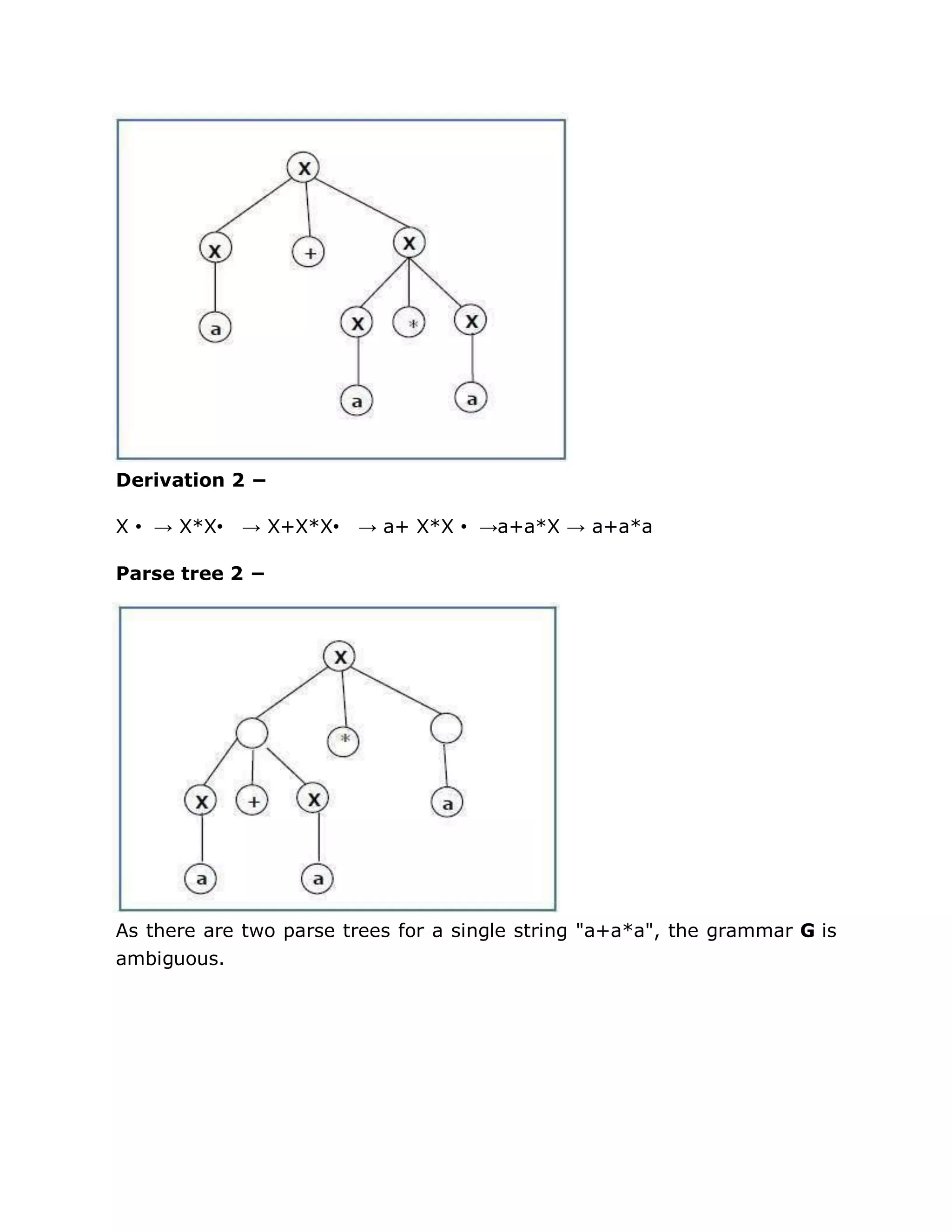


![Y2 = { S, A, C } from rule S → AC
Y3 = { S, A, C, a, c } from rules A → a and C → c
Y4 = { S, A, C, a, c }
Since Y3 = Y4, we can derive G” as −
G” = { { A, C, S }, { a, c }, P, {S}}
where P: S → AC, A → a, C → c
Removal of Unit Productions
Any production rule in the form A → B where A, B ∈ Non-terminal is
called unit production.
Removal Procedure −
Step 1 To remove A → B, add production A → x to the grammar rule wheneverB
→ x occurs in the grammar. [x ∈ Terminal, x can be Null]
Step 2 Delete A → B from the grammar.
Step 3 Repeat from step 1 until all unit productions are removed.
Problem
Remove unit production from the following −
S → XY, X → a, Y → Z | b, Z → M, M → N, N → a
Solution −
There are 3 unit productions in the grammar −
Y → Z, Z → M, and M → N
At first, we will remove M → N.
As N → a, we add M → a, and M → N is removed.
The production set becomes](https://image.slidesharecdn.com/automatatheory-151106083026-lva1-app6891/75/Automata-theory-59-2048.jpg)












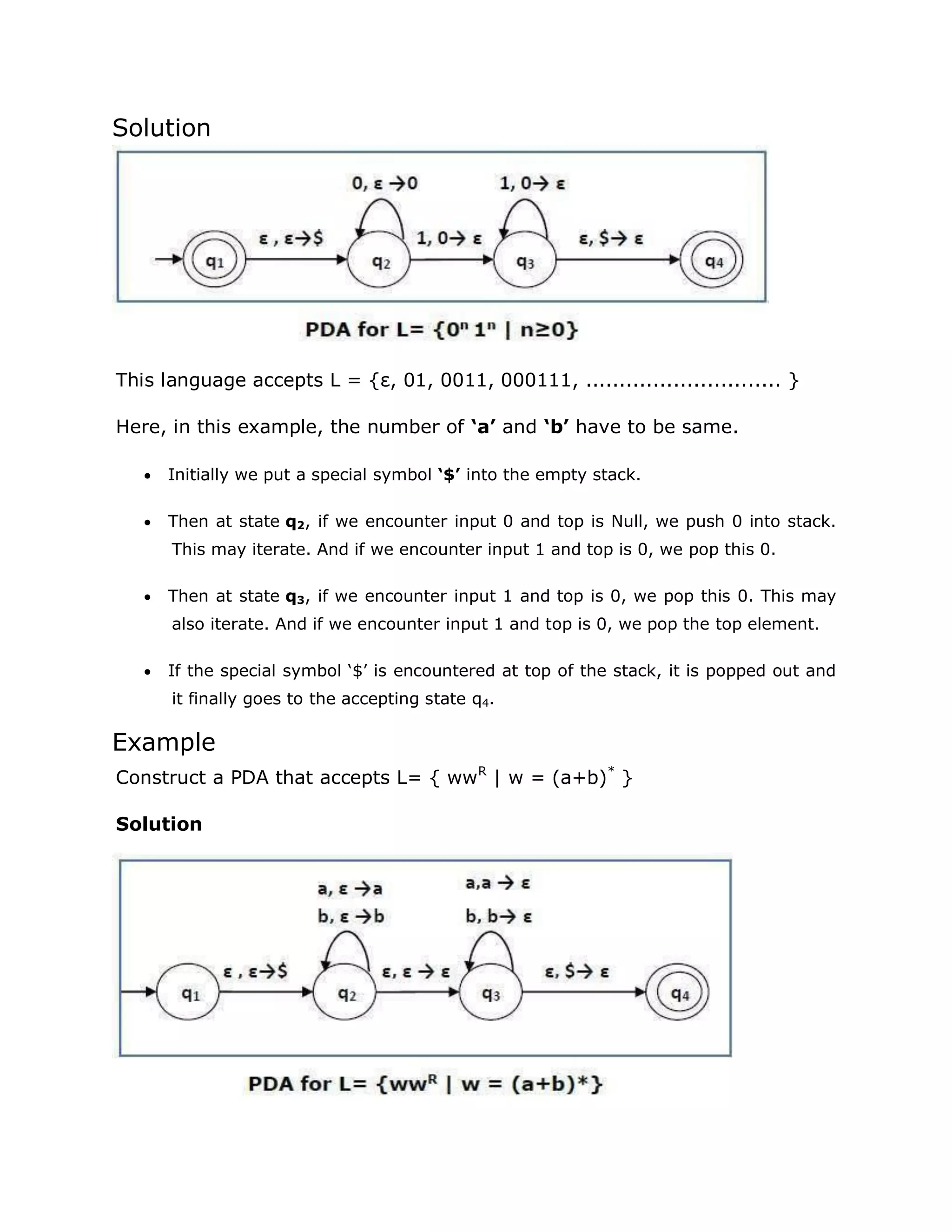





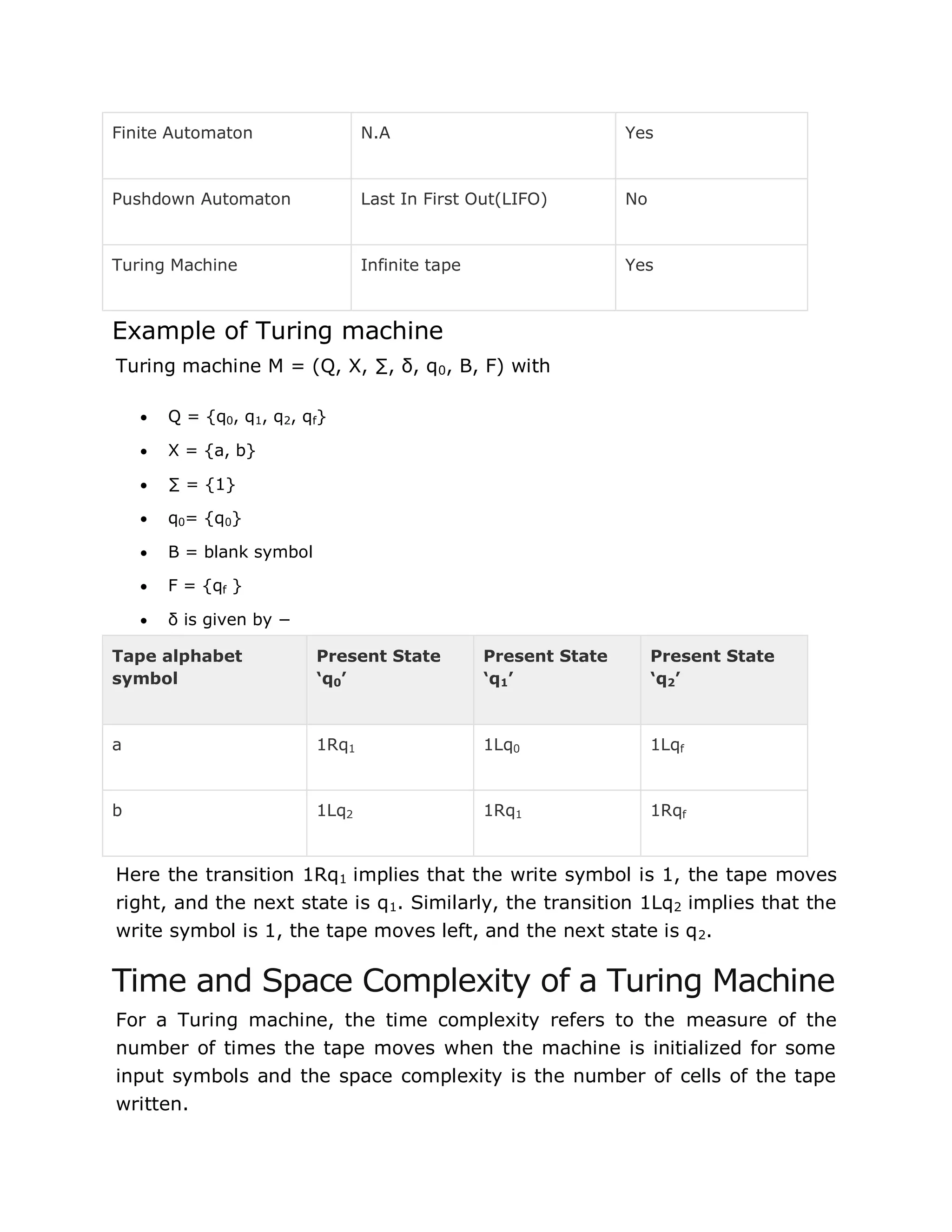


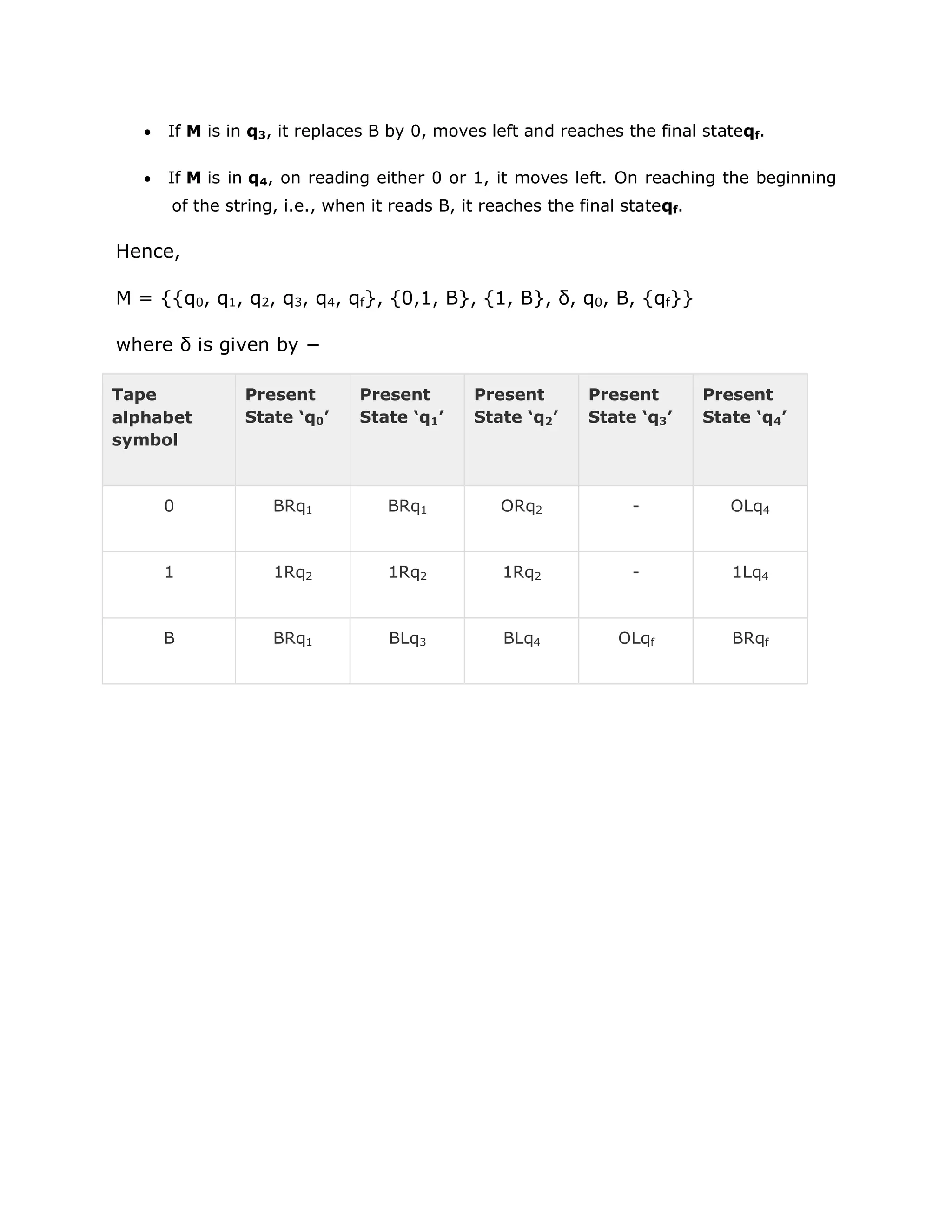

![Multi-track Turing Machine
Multi-track Turing machines, a specific type of Multi-tape Turing machine,
contain multiple tracks but just one tape head reads and writes on all
tracks. Here, a single tape head reads n symbols from n tracks at one step.
It accepts recursively enumerable languages like a normal single-track
single-tape Turing Machine accepts.
A Multi-track Turing machine can be formally described as a 6-tuple (Q, X,
∑, δ, q0, F) where −
Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
δ is a relation on states and symbols where
δ(Qi, [a1, a2, a3,....]) = (Qj, [b1, b2, b3,....], Left_shift or Right_shift)
q0 is the initial state
F is the set of final states
Note − For every single-track Turing Machine S, there is an equivalent
multi-track Turing Machine M such that L(S) = L(M).
Non-Deterministic Turing Machine
In a Non-Deterministic Turing Machine, for every state and symbol, there
are a group of actions the TM can have. So, here the transitions are not
deterministic. The computation of a non-deterministic Turing Machine is a
tree of configurations that can be reached from the start configuration.
An input is accepted if there is at least one node of the tree which is an
accept configuration, otherwise it is not accepted. If all branches of the
computational tree halt on all inputs, the non-deterministic Turing Machine](https://image.slidesharecdn.com/automatatheory-151106083026-lva1-app6891/75/Automata-theory-83-2048.jpg)