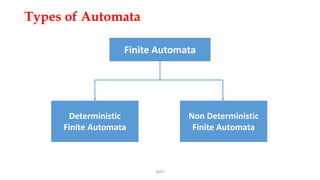
This document provides an introduction to finite automata. It defines key concepts like alphabets, strings, languages, and finite state machines. It also describes the different types of automata, specifically deterministic finite automata (DFAs) and nondeterministic finite automata (NFAs). DFAs have a single transition between states for each input, while NFAs can have multiple transitions. NFAs are generally easier to construct than DFAs. The next class will focus on deterministic finite automata in more detail.

1. INTRODUCTION
TO
FINITE AUTOMATA
M RATNAKAR BABU
Asst.Prof. CSE
KMIT

2. Alphabet
An alphabet is a finite and non empty set of symbols.
The example of alphabet is,
S={a, b, c,……..z}
The elements a, b, c, …….z are alphabets.
If W={0,1}
Here 0 and 1 are alphabets, denoted by W.
KMIT

3. String
• It is finite collection of symbols from alphabet.
For example, if  = {a,b} then various strings that can be formed
from  are {ab, ba, aaa, bbbb, aba, bab, ….}. An infinite number
of strings can be generated.
Language
• The language is a collection of appropriate strings.
• The language is defined using an input set. The input set is typically
denoted by letter .
For example:  ={Ꜫ,0,00,000,0000,….}.
Here the language L is defined as ‘Any number of Zeros’.
KMIT

4. Examples
1.The set of all strings over {a,b,c} that have ac as substring can be
written as {xacy | x,y ∈{a,b,c}∗}.
This can also be written as {x∈{a,b,c}∗ ||x|ac ≥1},
stating that the set of all strings over {a,b,c} in which the number
of occurrences of substring ac is at least 1.
2. The set of all strings over some alphabet Σ with even number of
a’s is {x∈Σ∗ ||x|a = 2n, for some n∈N}.
Equivalently, {x∈Σ∗ ||x|a ≡ 0 mod 2}.
3. The set of all strings over some alphabet Σ with equal number
of a’s and b’s can be written as {x∈Σ∗ ||x|a =|x|b}.
4. The set of all palindromes over an alphabet Σ can be written as
{x∈Σ∗ | x = xR}, where xR is the string obtained by reversing x.
KMIT

5. Finite State Machine
• The finite state machine represents a mathematical model of a
system with certain input.
• The model finally gives certain output.
• The input is processed by various states, these states are called as
intermediate states.
• The finite state system is very good design tool for the programs such
as TEXT EDITORS and LEXICAL ANALYZERS.
KMIT

6. Definition of Finite Automata
• A finite automata is a collection of 5-tuple(Q,,,q0,F) Where ,
Q is finite set of states, which is non empty.
 is input alphabet, indicates input set.
 is transition function or mapping function. We can determine
the next state using this function.
q0 is an initial state and is in Q
F is set of final states.
KMIT

7. Finite Automata Model
• The finite automata can be represented as follows:
A B A B A B A B A B
Finite
Control
Input Tape
Tape
Reader Input Tape: It is a linear tape
having some number of cells. Each
input symbol is placed in each cell.
Finite Control: The finite control
decides the next state on receiving
particular input from input tape.
KMIT
Out put

8. Types of Automata
Finite Automata
Deterministic
Finite Automata
Non Deterministic
Finite Automata
KMIT

9. Types of Automata
• Deterministic Finite Automata: The Finite Automata is called
Deterministic Finite Automata if there is only one path for a specific
input from current state to next state.
It can be represented as follows:
• A machine M = (Q,,,q0,F) Where ,
Q is finite set of states, which is non empty.
 is input alphabet, indicates input set.
 is transition function or mapping function. We can determine
the next state using this function.
q0 is an initial state and is in Q
F is set of final states.
Where :Q X  -> Q KMIT

10. Types of Automata
• Non Deterministic Finite Automata: The Finite Automata is called
Non Deterministic Finite Automata if there are more than one path
for a specific input from current state to next state.
It can be represented as follows:
• A machine M = (Q,,,q0,F) Where ,
Q is finite set of states, which is non empty.
 is input alphabet, indicates input set.
 is transition function or mapping function. We can determine
the next state using this function.
q0 is an initial state and is in Q
F is set of final states.
Where :Q X  -> 2Q KMIT

11. Difference between DFA & NFA
Deterministic Finite Automata Non Deterministic Finite Automata
For Every symbol of the alphabet, there is only one
state transition in DFA.
We do not need to specify how does the NFA react
according to some symbol.
DFA cannot use Empty String transition. NFA can use Empty String transition.
DFA can be understood as one machine. NFA can be understood as multiple little machines
computing at the same time.
DFA will reject the string if it end at other than
accepting state.
If all of the branches of NFA dies or rejects the string,
we can say that NFA reject the string.
Backtracking is allowed in DFA. Backtracking is not always allowed in NFA.
DFA is more difficult to construct. NFA is easier to construct.
KMIT

12. Summary
• From this session we have seen what is Finite Automata
• Types of Automata.
KMIT

13. Next Class
• In the next session we are going to learn about
Deterministic Finite Automata
KMIT

14. END For NOW
Continue in next class
KMIT