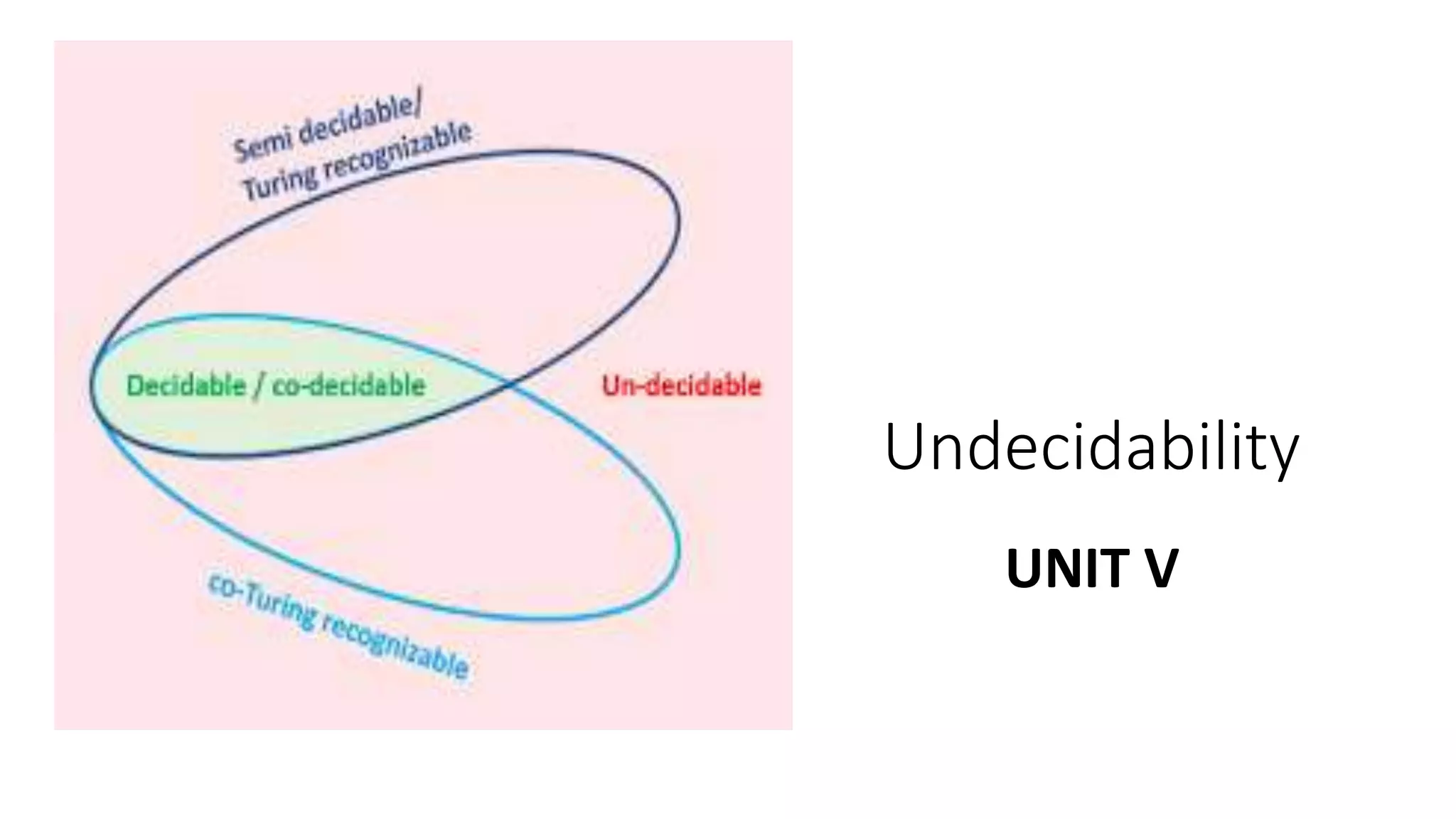
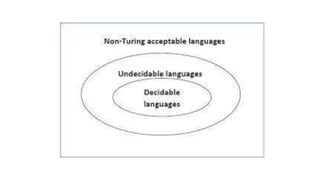
This document discusses undecidable problems. It begins by mentioning Turing and Gödel's work showing there are true statements that cannot be proven. Specifically, Gödel constructed a self-referential statement like "I am not provable" whose truth cannot be determined. The document then notes that while computers can solve many problems, there are problems that cannot be solved by any computer no matter the resources. It defines a decidable language as one where a Turing machine can accept the language and always halt on every input string. Examples are given of undecidable problems related to context-free languages like determining ambiguity or equivalence.

1. Undecidability
UNIT V

2. Introduction
Alan Turing first proved this result in 1936. It is related to Gödel's
Incompleteness Theorem, which states that there is no system of logic
strong enough to prove all true sentences of number theory.
Essentially, Gödel uses a fix point construction to construct a self-
referential sentence of number theory which states something to the
effect: "I am not provable".
The argument is quite complex. However, the argument is basically
analogous to the one given in support of the fact that the truth value of
the statement ‘I am telling lies’ can not be determined.

3. Cont…
In view of the large number of applications of modern computer systems
that help us in solving problems from almost every domain of human
experience, you might be tempted to think that computers can solve any
problem if the problem is properly formulated.
 We will prove that such problems cannot be solved no matter.
• What language is used?
• What machine is used?
• Much computational resources are devoted in attempting to solve the problem, etc.
For problems that cannot be solved by computational means, we can
approximate their solutions, but it's impossible to get the perfectly correct
solutions in all cases.

4. Decidable Languages
• A language is decidable,
• if there is a Turing machine (decider)
• that accepts the language and
• halts on every input string

6. Examples
•Ambiguity of context-free languages: Given a context-free
language, there is no Turing machine which will always halt in
finite amount of time and give answer whether language is
ambiguous or not.
•Equivalence of two context-free languages: Given two
context-free languages, there is no Turing machine which will
always halt in finite amount of time and give answer whether
two context free languages are equal or not.
•Everything or completeness of CFG: Given a CFG and
input alphabet, whether CFG will generate all possible strings
of input alphabet (∑*)is undecidable.
•Regularity of CFL, CSL, REC and REC: Given a CFL, CSL,
REC or REC, determining whether this language is regular is
undecidable.