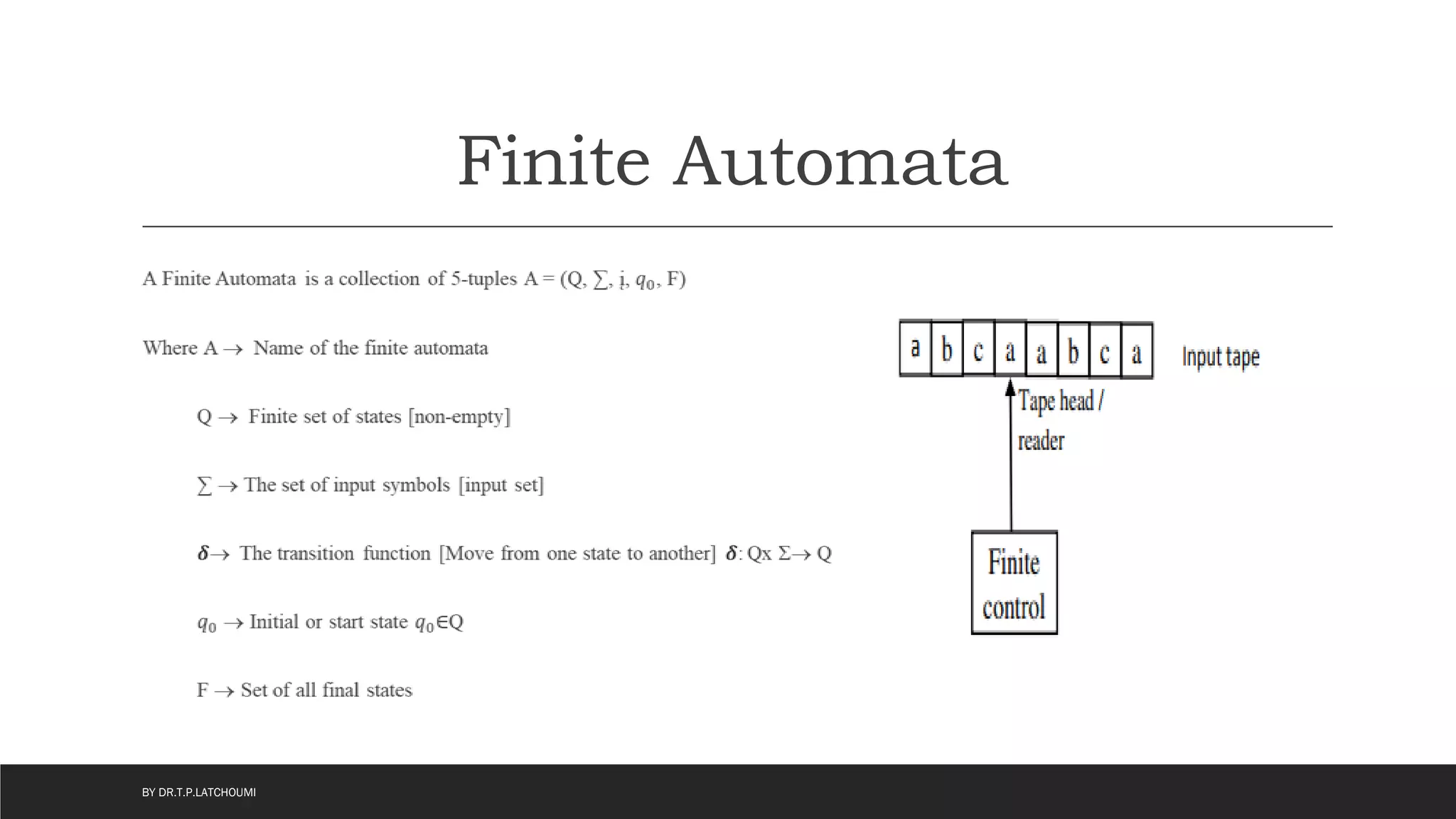
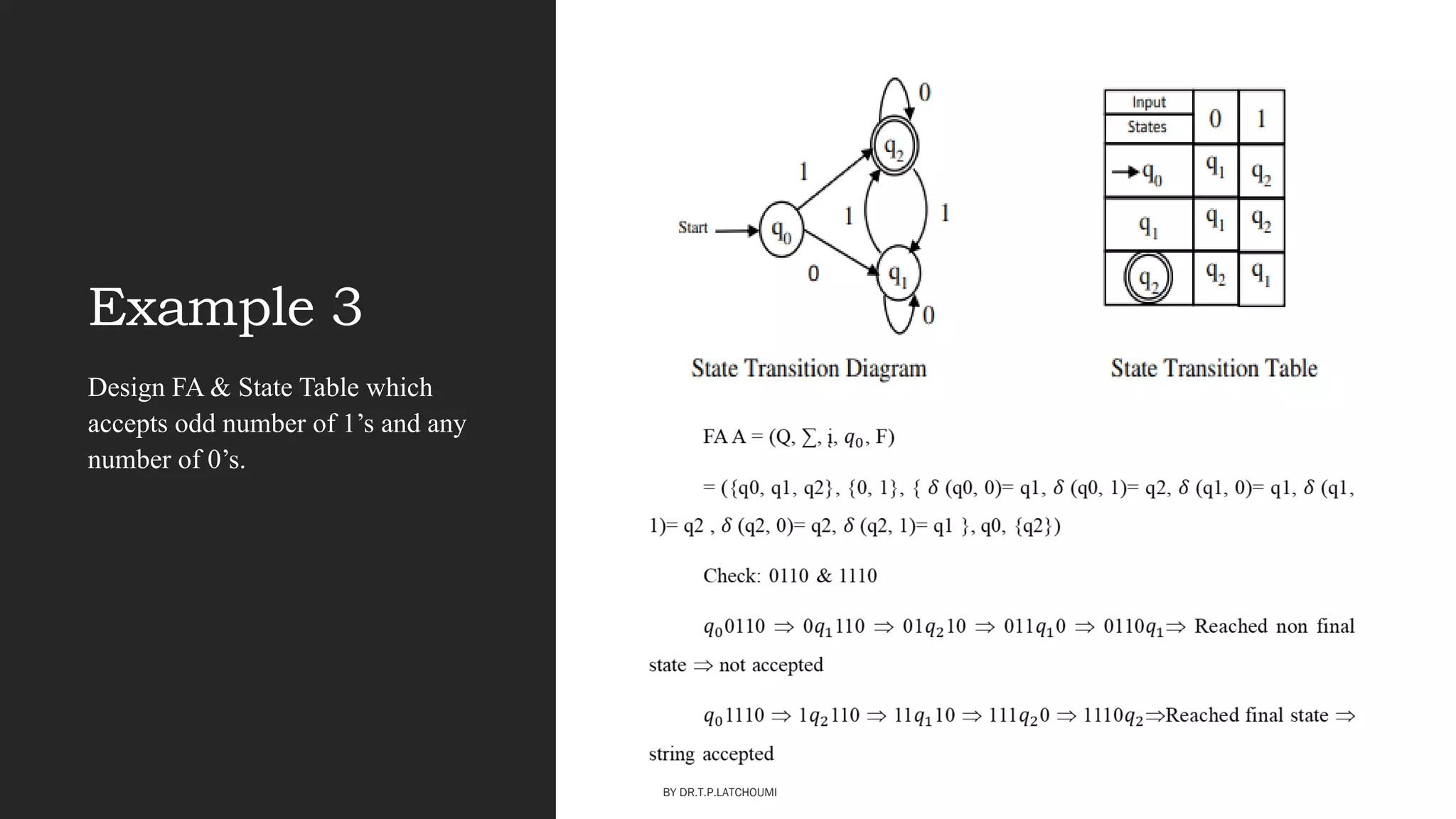
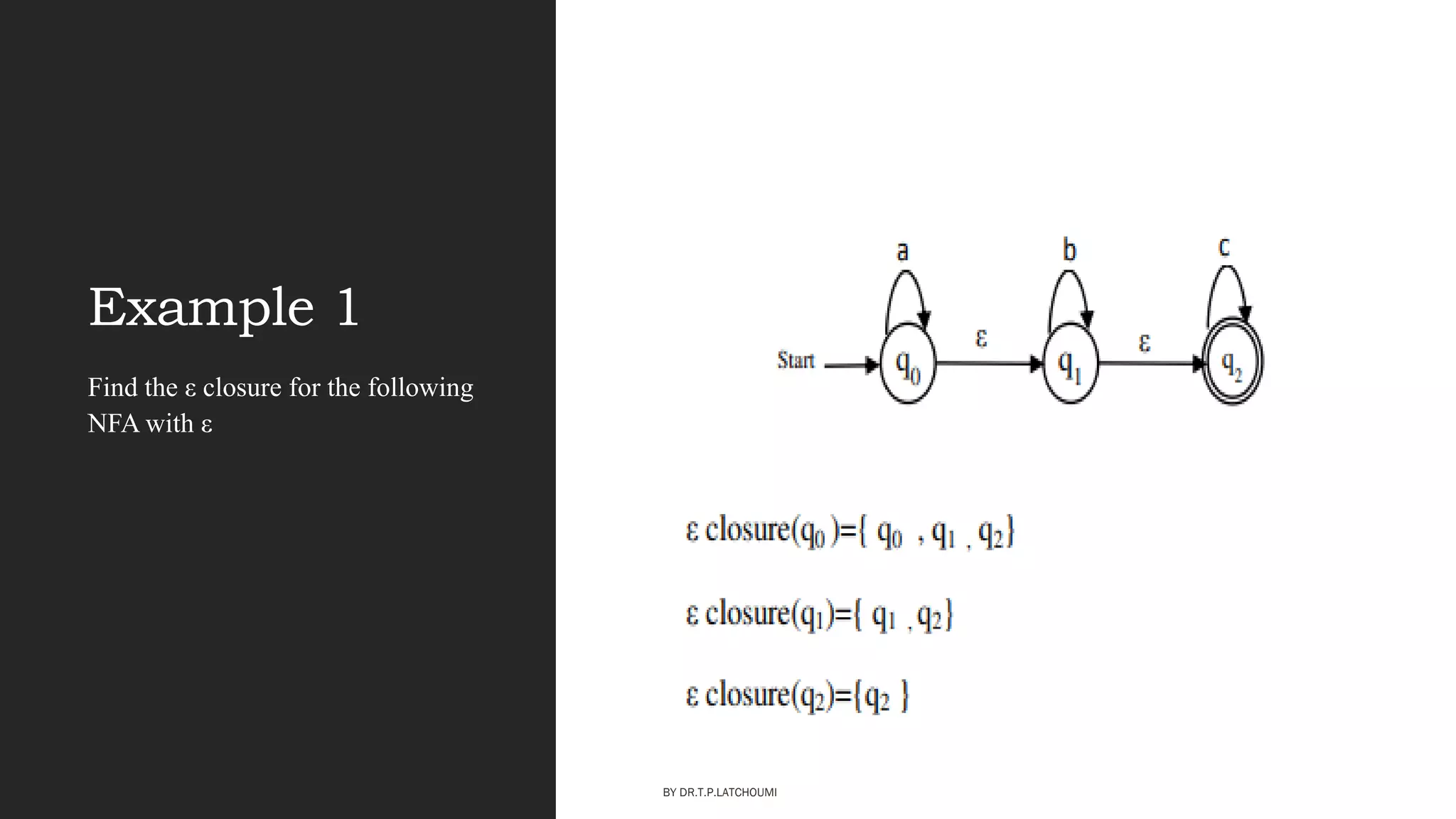
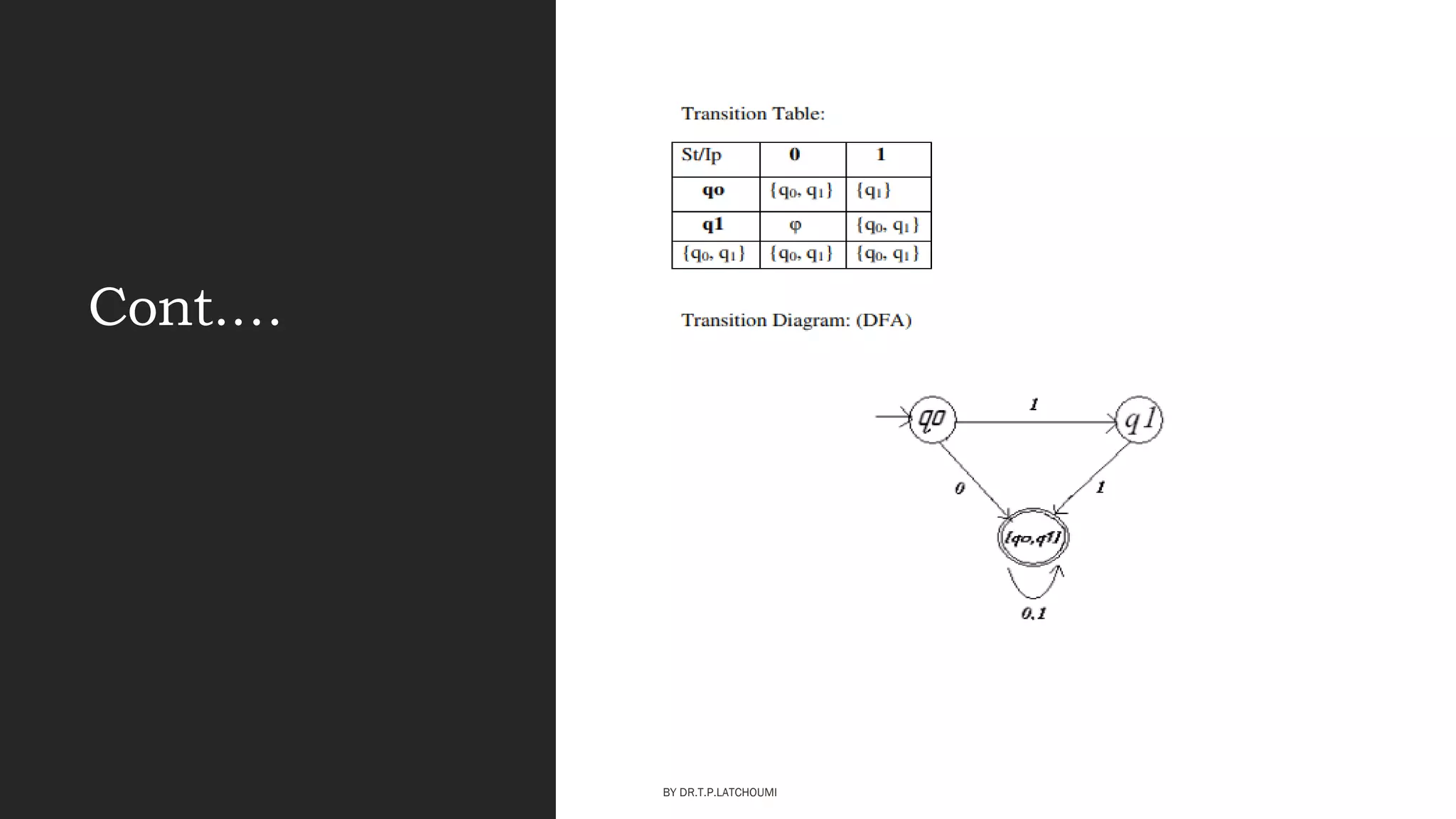
The document provides an introduction to the concepts and topics covered in the course "Introduction to Automata Theory". It discusses key concepts such as automata, formal languages, strings, regular expressions, finite automata including deterministic finite automata (DFA) and nondeterministic finite automata (NFA). Examples of DFAs and NFAs are provided to recognize specific languages. The document also introduces the pioneer of automata theory, Alan Turing, and explains the importance and applications of automata theory.




















![Example :2
Let n = 1, P(1) = 42(1) + 1 + 3(1) + 2= 43 + 33 = 64 + 27 = 91 = 13.t where t= 7
Let n = k, P(k) = 42(k) + 1 + 3(k) + 2= 42k + 1 + 3k + 2 = 13.t, true for some integer t
Let n = k + 1, P(k + 1) = 42(k + 1) + 1 + 3(k + 1) + 2
= 42(k + 1) + 1 + 3(k + 1) + 2
= 42k + 2 + 1 + 3k + 1 + 2
= 42k + 1 + 2 + 3k + 2 + 1
= 42k + 1.42 + 3k + 2.31
= 42.42k + 1 + 3.3k + 2
= 42.42k + 1 + 423k+2 - 423k+2 + 3.3k + 2 {Add & Sub 423k+2}
= 42(42k + 1 + 3k+2) + 3k+2 (-42+ 3)
= 42(13.t)- 3k+2 (-42+ 3) {42k + 1 + 3k + 2 = 13.t} = 16(13.t)- 3k+2 (-13)
= 13[16. t + 3k+2] = Multiple of 13
P(k + 1) is multiple of 13, Hence proved.
Prove that every integer n ≥ 0, the
number 42n + 1 + 3n + 2 is multiple of
13 by induction.
BY DR.T.P.LATCHOUMI](https://image.slidesharecdn.com/uniti-220111055426/75/Unit-i-21-2048.jpg)


![String
A string is a finite sequence of symbols chosen from some alphabet.
1) Σ = {0,1} 11001 [ Empty string is denoted by ε]
2) Σ = {a, b, c} aabbcbbbaa
The total number of symbols in the string is called length of the string
Example: 1) |0001|=4
2) |100|=3
BY DR.T.P.LATCHOUMI](https://image.slidesharecdn.com/uniti-220111055426/75/Unit-i-24-2048.jpg)