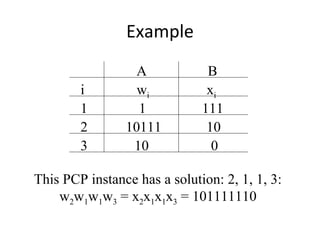
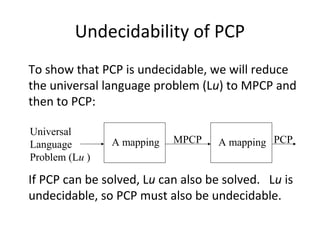
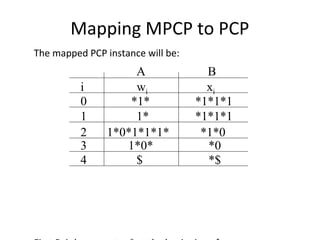
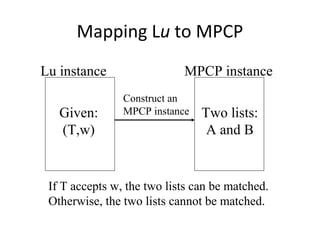
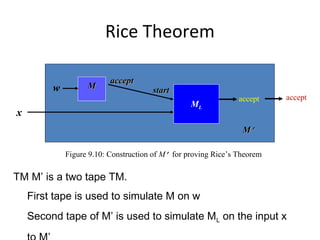
The document discusses the Post Correspondence Problem (PCP) and shows that it is undecidable. It defines PCP as determining if there is a sequence of string pairs from two lists A and B that match up. It then defines the Modified PCP (MPCP) which requires the first pair to match. It shows how to reduce the Universal Language Problem to MPCP by mapping a Turing Machine and input to lists A and B, and then how to reduce MPCP to PCP. Finally, it discusses Rice's Theorem and how properties of recursively enumerable languages are undecidable.

1. POST’s CORRESPONDENCE PROBLEM

2. • General Objective:
– to understand the concept of PCP
• Specific Objectives
– State the objective of PCP
– Define PCP problem
– Check whether the PCP instance have a solution or not.
– Define MPCP
– Illustrate the conversion of TM to MPCP with an example

3. Post Correspondence Problem
• It involves with strings
• Goal:
– To prove this problem about strings to be
undecidable

4. Post Correspondence Problem
• FORMAL DEFINITION
Given two lists of strings A and B ( equal length)
A = w1, w2, …, wk B = x1, x2, …, xk
The problem is to determine if there is a sequence of
one or more integers i1, i2, …, im such that:
wi1
wi2
…wim
= xi1
xi2
…xim
(w, x) is called a corresponding pair.

5. Example
A B
i
1
2
3
wi
1
10111
10
xi
111
10
0
This PCP instance has a solution: 2, 1, 1, 3:
w2w1w1w3 = x2x1x1x3 = 101111110

6. Does this PCP instance have a solution?
A B
i
1
2
3
wi
110
0011
0110
xi
110110
00
110
This PCP instance has a solution: 2,3,1
w2w3w1 = x2x3x1 = 00110110110
One more solution:
2,1,1,3,2,1,1,3

7. Modified Post Correspondence
Problem (MPCP)
Definition:
first pair in the A and B lists must be the first pair in the
solution, i.e., the problem is to determine if there is a
sequence of zero or more integers i1, i2, …, im such that:
w1wi1
wi2
…wim
= x1xi1
xi2
…xim

8. Modified Post Correspondence
Problem (MPCP)
List A List B
i wi xi
1 10 10
2 110 11
3 11 011
This MPCP instance has a solution: 1,2,3
w1 w2 w3 = x1 x2 x3
10 110 11 = 10 11 011

9. Undecidability of PCP
To show that PCP is undecidable, we will reduce
the universal language problem (Lu) to MPCP and
then to PCP:
If PCP can be solved, Lu can also be solved. Lu is
undecidable, so PCP must also be undecidable.
Universal
Language
Problem (Lu )
MPCP PCPA mapping A mapping

10. Reducing MPCP to PCP
• This can be done by inserting a special symbol
(*) to the strings in list A and B of to make
sure that the first pair will always go first in
any solution.
• List A : * follows the symbols of ∑
• List B : * precedes the symbols of ∑
• wk+1 = $ ; xk+1 = *$

11. Mapping MPCP to PCP
Suppose the original MPCP instance is:
A B
i
1
2
3
wi
1
10111
10
xi
111
10
0

12. Mapping MPCP to PCP
The mapped PCP instance will be:
A B
i
0
1
2
wi
*1*
1*0*1*1*1*
1*0*
xi
*1*1*1
*1*0
*03
4
1* *1*1*1
$ *$

13. Mapping Lu to MPCP
• Turing machine M and an input w, we want to
determine if M will accept w.
• the mapped MPCP instance should have a
solution if and only if M accepts w.

14. Mapping Lu to MPCP
Given:
(T,w)
Two lists:
A and B
Construct an
MPCP instance
If T accepts w, the two lists can be matched.
Otherwise, the two lists cannot be matched.
Lu instance MPCP instance

15. Rules of Reducing Lu to MPCP
• We summarize the mapping as follows. Given
T and w, there are five types of strings in list A
and B:
• Starting string (first pair):
List A List B
# #q0w#
where q0 is the starting state of T.

16. • Strings for copying:
List A List B
X X
# #
where X is any tape symbol (including the
blank).
# is a separator can be appended to both the
lists

17. • Strings from the transition function δ:
List AList B
qX Yp from δ(q,X)=(p,Y,R)
ZqX pZY from δ(q,X)=(p,Y,L)
q# Yp# from δ(q,#)=(p,Y,R)
Zq# pZY# from δ(q,#)=(p,Y,L)
where Z is any tape symbol except the blank.

18. • Strings for consuming the tape symbols at
the end:
List AList B
Xq q
qY q
XqY q
where q is an accepting state, and each X
and Y is any tape symbol except the blank.

19. • Ending string:
List A List B
q## #
where q is an accepting state.
• Using this mapping, we can show that the
original Lu instance has a solution if and only
if the mapped MPCP instance has a solution.

20. PCP is undecidable
• Theorm: Post’s Correspondence Problem is undecidable.
• We have seen the reduction of MPCP to PCP
• now we see how to reduce Lu to MPCP.
– M accepts w if and only if the constructed MPCP instance has a
solution.
– As Lu is undecidable, MPCP is also undecidable.

21. Rice Theorem
• Rice’s Theorem & Properties of RE Languages
– A property is trivial if it is either empty or is the
set of all RE languages; otherwise, nontrivial.
– Examples:
• The empty property, φ, is different from the
property of being an empty language, {φ}.

22. Undecidable Problems about
Turing Machines
• Nontrivial Properties of RE (Undecidable)
– Emptiness
– Finiteness
– Regularity
– Context-Free

23. Rice Theorem
• Theorem:
– Every nontrivial property of the RE language is
undecidable.
• Proof:
– Let P be the nontrivial property of RE.
– Assume Ø, the empty language is not in P
– Since P is nontrivial, there must be some non-
empty language L is in P
– Let MLbe a TM accepting L.

24. Rice Theorem
• Reduce Luto Lp thus proving Lp is undecidable since Lu is
undecidable.
• The algorithm to perform the reduction takes as input a
pair (M,w) and produces a TM M’.
– L(M’) = Ø if M does not accept w
– L(M’) = L if M accepts w

25. Rice Theorem
MM’’
ML
MM
acceptaccept
x
Figure 9.10: Construction of M’ for proving Rice’s Theorem
accept accept
w startstart
TM M’ is a two tape TM.
First tape is used to simulate M on w
Second tape of M’ is used to simulate ML on the input x

26. 26
Undecidable Problems about
Turing Machines
• Problems about TM Specifications
– The following are undecidable accordingly:
• Whether the language accepted by a TM is empty
• Whether the language accepted by a TM is finite.
• Whether the language accepted by a TM is a regular
language.
• Whether the language accepted by a TM is a context-free
language.