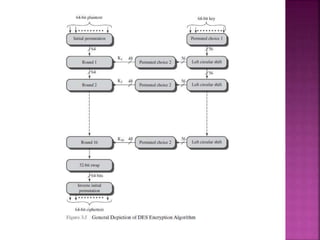
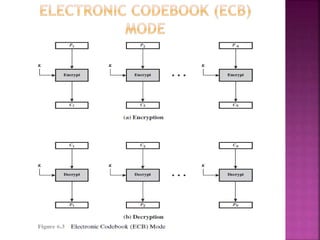
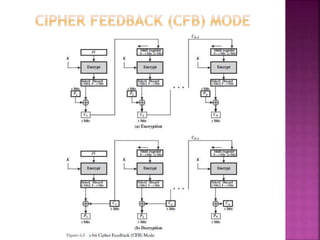
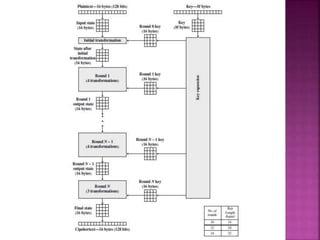
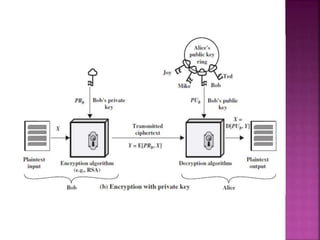
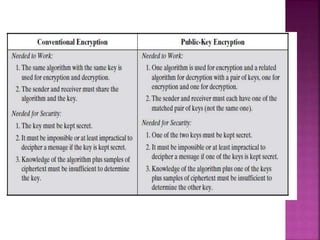
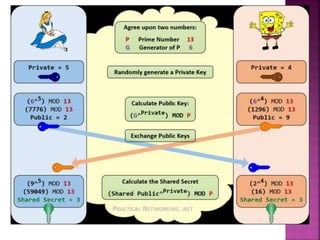
The document discusses stream ciphers and block ciphers. It explains that stream ciphers encrypt data bit-by-bit or byte-by-byte, requiring a randomly generated keystream, while block ciphers encrypt fixed-length blocks, allowing for broader applications. It then focuses on the Feistel cipher structure for block ciphers, proposed by Feistel to approximate an ideal block cipher for large block sizes. The Feistel structure uses a product cipher approach involving substitutions and permutations to provide diffusion and confusion and resist statistical cryptanalysis.

1. V.Thamizharasan
Assistant professor
Department of ECE
Erode Sengunthar
Engineering College

2.  Feistel block cipher-- block encryption
algorithms – basic structure
 stream ciphers and block ciphers

3. STREAM CIPHER
 encrypts a digital data stream one bit or one byte
at a time.
 Vigenère cipher and the Vernam cipher.
 keystream is random cipher is unbreakable.
 keystream must be provided to both users in
advance.
 This introduces insurmountable logistical problems
if the intended data traffic is very large

4.  block of plaintext is treated as a whole and
used to produce a ciphertext block of equal
length.
 block size of 64 or 128 bits is used.
 block cipher is broader range of applications
than stream ciphers.

5.  plaintext block of n bits to produce a
ciphertext block of n bits
 Reversible or nonsingular
2^n possible different plaintext blocks and, for the
encryption to be reversible (i.e., for decryption to be
possible), each must produce a unique ciphertext block.
Feistel cipher structure

8.  n = 4 classical substitution cipher
 vulnerable to a statistical analysis of the
plaintext.
If n is sufficiently large cryptanalysis is
infeasible
 An arbitrary reversible substitution cipher
(the ideal block cipher) for a large block size
is not practical.
 required key length is (4 bits) * (16 rows) =
64 bits.
 In general n * 2^n bits.
 64-bit block64 * 2^64 = 2^70= 10^21 bits.
 thwart statistical attacks.

9.  considering these difficulties
 Feistel points out that what is needed is an
approximation to the ideal block cipher system
for large n.

10.  Feistel proposed approximate the ideal block
cipher by utilizing the concept of a product cipher.
 execution of two or more simple ciphers
cryptographically stronger
 The essence of the approach is to develop a block cipher
with a key length of k bits and a block length of n bits
allowing a total of 2^k possible transformations, rather
than the 2^n! transformations available with the ideal
block cipher
 Feistel proposeduse of a cipher that alternates
substitutions and permutations

11.  Feistel’s is a practical application of a proposal by
Claude Shannon to develop a product cipher that
alternates confusion and diffusion functions
 thwart cryptanalysis based on statistical analysis
 the attacker has some knowledge of the statistical
characteristics of the plaintext.
 In what Shannon refers to as a strongly ideal cipher,
all statistics of the ciphertext are independent of
the particular key used

12.  Diffusion:
 statistical structure of the plaintext is
dissipated into long-range statistics of the
ciphertext.
 This is achieved by having each plaintext
digit affect the value of many ciphertext
digits.
 this is equivalent to having each ciphertext
digit be affected by many plaintext digits

13.  The mechanism of diffusion seeks to make the
statistical relationship between the plaintext
and ciphertext as complex as possible in order
to thwart attempts to deduce the key.
 On the other hand, confusion seeks to make the
relationship between the statistics of the
ciphertext and the value of the encryption key
as complex as possible, again to thwart
attempts to discover the key.
 complex substitution algorithm. In contrast, a
simple linear substitution function would add
little confusion

15.  Block size:
Larger block sizes mean greater security but reduced
encryption/decryption speed for a given algorithm
 Key size:
 Larger key size means greater security but may decrease
encryption/decryption speed
 Number of rounds:
single round offers inadequate security but that multiple rounds
offer increasing security. A typical size is 16 rounds
 Sub key generation algorithm:
Greater complexity in this algorithm should lead to greater
difficulty of cryptanalysis
 Round function F:
greater complexity generally means greater resistance to
cryptanalysis

17.  DES was the most widely used encryption
scheme
 DES was issued
 1977 by the National Bureau of Standards
 now the National Institute of Standards and
Technology (NIST), as Federal Information
Processing Standard 46 (FIPS PUB 46)
 Data Encryption Algorithm (DEA)
 64-bit blocks using a 56-bit key

19.  A desirable property of any encryption algorithm
is that a small change in either the plaintext or
the key should produce a significant change in
the ciphertext.
 a change in one bit of the plaintext or one bit of
the key should produce a change in many bits of
the ciphertext. This is referred to as the
avalanche effect.

20.  Three critical aspects of block cipher design:
1. the number of rounds,
 The greater the number of rounds, the more difficult it is to
perform cryptanalysis, even for a relatively weak F.
2. Design of the function F
 The heart of a Feistel block cipher is the function F, which
provides the element of confusion in a Feistel cipher
 One obvious criterion is that F be nonlinear
 The more nonlinear F, the more difficult any type of
cryptanalysis will be
 strict avalanche criterion (SAC)
which states that any output bit j of an S-box should change
with probability 1/2 when any single input bit i is inverted
for all i, j.

21. bit independence criterion
 which states that output bits j and k should change
independently when any single input bit i is inverted for all i,
j, and k.
3.key scheduling.
 With any Feistel block cipher, the key is used to generate one
subkey for each round. In general, we would like to select
subkeys to maximize the difficulty of deducing individual
subkeys and the difficulty of working back to the main key.

29.  Private key symmetric block cipher
 128-bit data, 128/192/256-bit keys
 Stronger & faster than Triple-DES
 Provide full specification & design details
 Both C & Java implementations

30. 30
AES
Plaintext (128 bits)
Ciphertext (128 bits)
Key (128-256 bits)

32. 32
 Rounds are (almost) identical
 First and last round are a little different

33. • Round keys are derived from the cipher
key using Rijndael's key schedule
Key
Expansion
• AddRoundKey : Each byte of the state is
combined with the round key using bitwise xorInitial Round
• SubBytes : non-linear substitution step
• ShiftRows : transposition step
• MixColumns : mixing operation of each
column.
• AddRoundKey
Rounds
• SubBytes
• ShiftRows
• AddRoundKey
Final Round No MixColumns

35.  A simple substitution of each byte
 provide a confusion
 Uses one S-box of 16x16 bytes containing a permutation of all 256
8-bit values
 Each byte of state is replaced by byte indexed by row (left 4-bits)
& column (right 4-bits)
 eg. byte {95} is replaced by byte in row 9 column 5
 which has value {2A}
 S-box constructed using defined transformation of values in
Galois Field- GF(28)

37.  The SubBytes operation involves 16 independent byte-
to-byte transformations. • Interpret the byte as two
hexadecimal digits xy
• SW implementation, use row (x)
and column (y) as lookup pointerS1,1 = xy16
x’y’16

38.  Implement by Table Lookup

41.  The SubBytes and InvSubBytes transformations are
inverses of each other.

42.  Last three rows are cyclically shifted
S0,0 S0,1 S0,2 S0,3
S1,0 S1,1 S1,2 S1,3
S2,0 S2,1 S2,2 S2,3
S3,0 S3,1 S3,2 S3,3
S1,0
S3,0 S3,1 S3,2
S2,0 S2,1

47. 1. key distribution
symmetric encryption requires either
1. that two communicants already share a key
2. key distribution center.
2. digital message had been sent by a
particular person?

54.  cipher in which the plaintext and ciphertext
are integers between 0 and n - 1 for some n
 A typical size for n is 1024 bits, or 309
decimal digits. That is, n is less than 2^1024.

59.  Why ECC?
Good security even with for smallest key than
RSA
Reducing the processing over head.
 Basics of ECC:
Abelian Groups

60.  Diffie-Hellman key exchange involves multiplying
pairs of nonzero integers modulo a prime number
q.
Elliptic Curve Cryptography, An Operation Over
Elliptic Curves, Called Addition, Is Used.
Multiplication Is Defined By Repeated Addition.
An elliptic curve is defined by an equation in
two variables with coefficients.

61. In general, cubic equations for elliptic curves take the following
form, known as a Weierstrass equation:
where a, b, c, d, e are real numbers and x and y take on values in
the real numbers
For our purpose, it is sufficient to limit ourselves to equations of
the form
For given values of a and b, the plot consists of positive and
negative values of y for each value of x.
Thus, each curve is symmetric about y = 0.

63.  Let a ∈ ℝ, b ∈ ℝ, be constants such that
4a³ + 27b² ≠ 0. A non-singular elliptic
curve is the set E of solutions (x,y) ∈ ℝ x ℝ
to the equation:
y² = x³ + ax + b
together with a special point O called the
point at infinity.

64.  If 4a³ + 27b² = 0, then we have a singular
elliptic curve
 This could potentially lead to having to
not having 3 distinct roots
 Therefore, we must deal with non-
singular elliptic curves with the condition
4a³ + 27b² ≠ 0, in order to assure that
we have 3 distinct roots.
 This will allow us to establish the fact
that the solution set E forms an Abelian
group.

67.  Elliptic curve cryptography makes use of
elliptic curves in which the variables and
coefficients are all restricted to elements of
a finite field.
 Two families of elliptic curves are used in
cryptographic applications:
 Prime curves over Zp
we use a cubic equation in which the variables and
coefficients all take on values in the set of integers from 0
through p - 1 and in which calculations are performed
modulo p.
 best for software applications
 Binary curves over GF(2^m)
 the variables and coefficients all take on values in
GF(2^m) and in calculations are performed over GF(2^m).
 best for hardware applications,