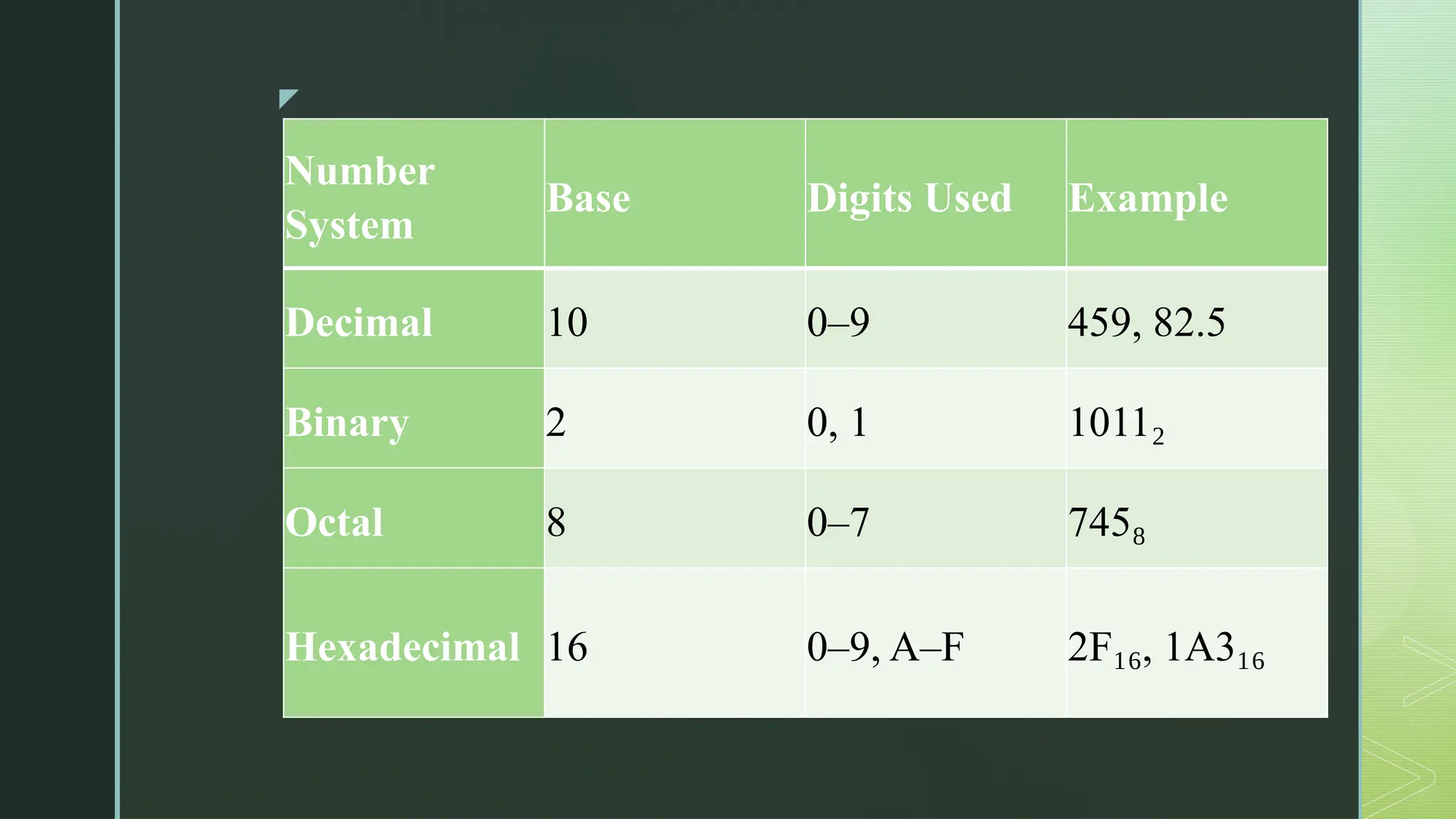
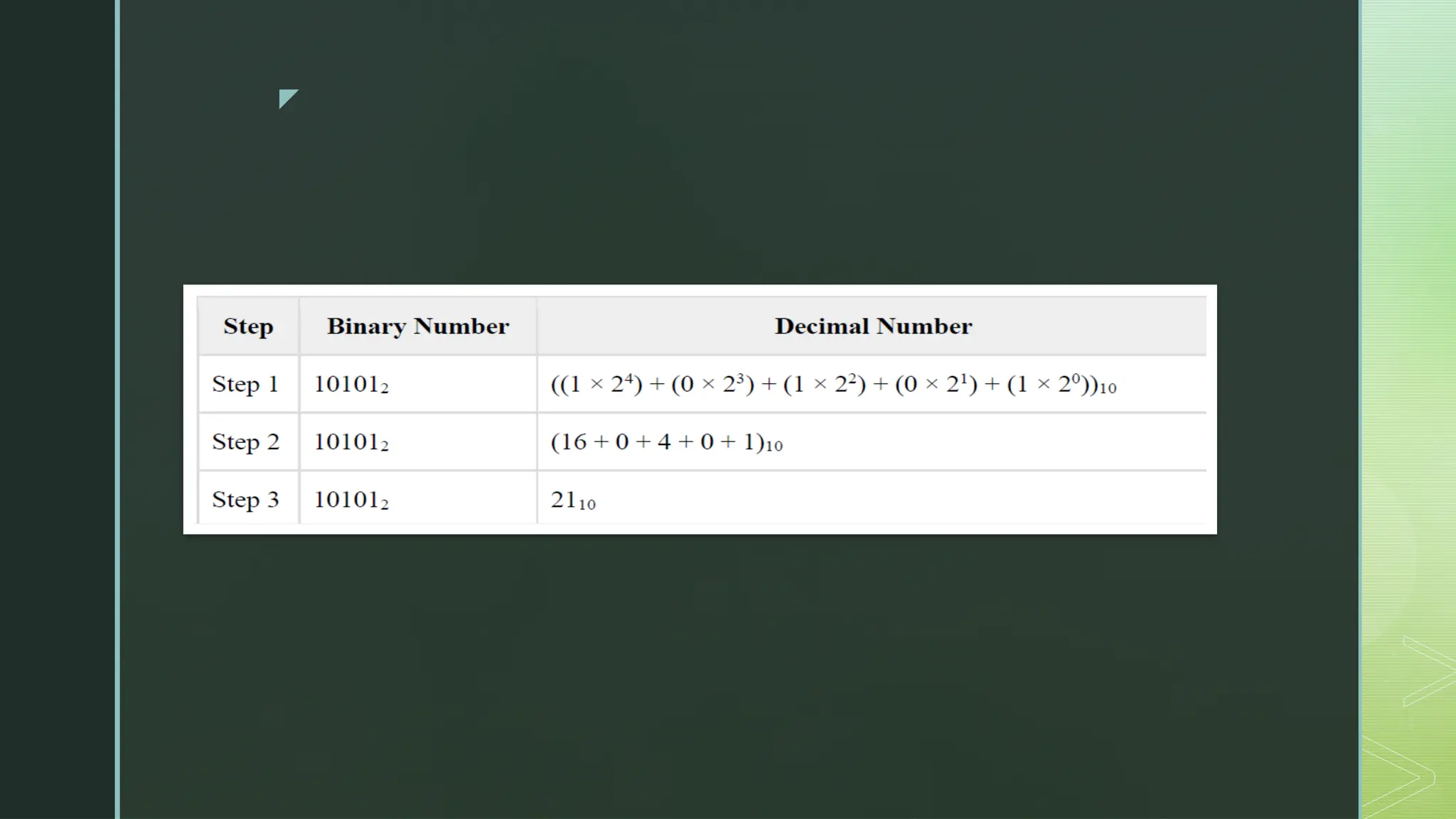
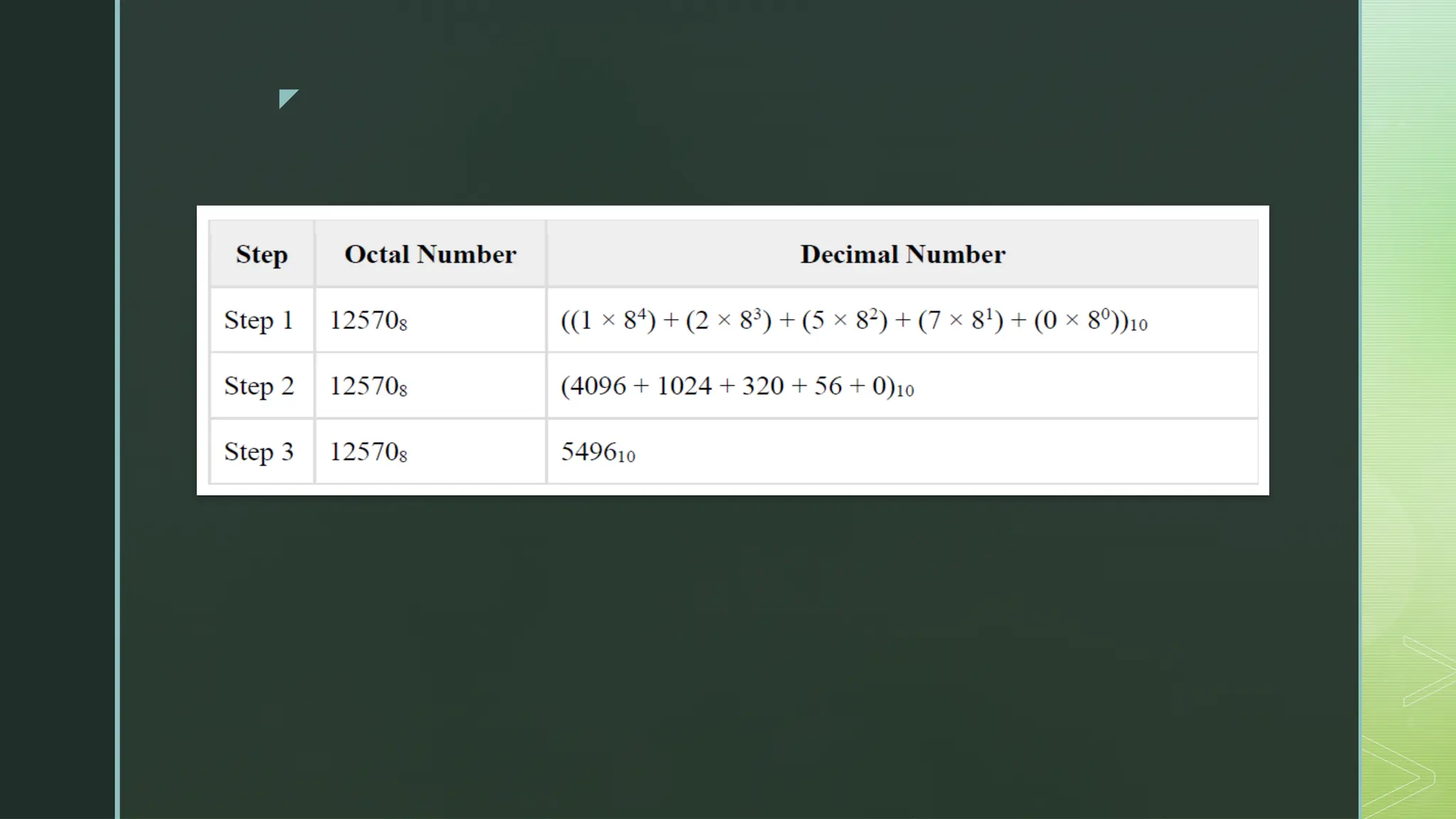
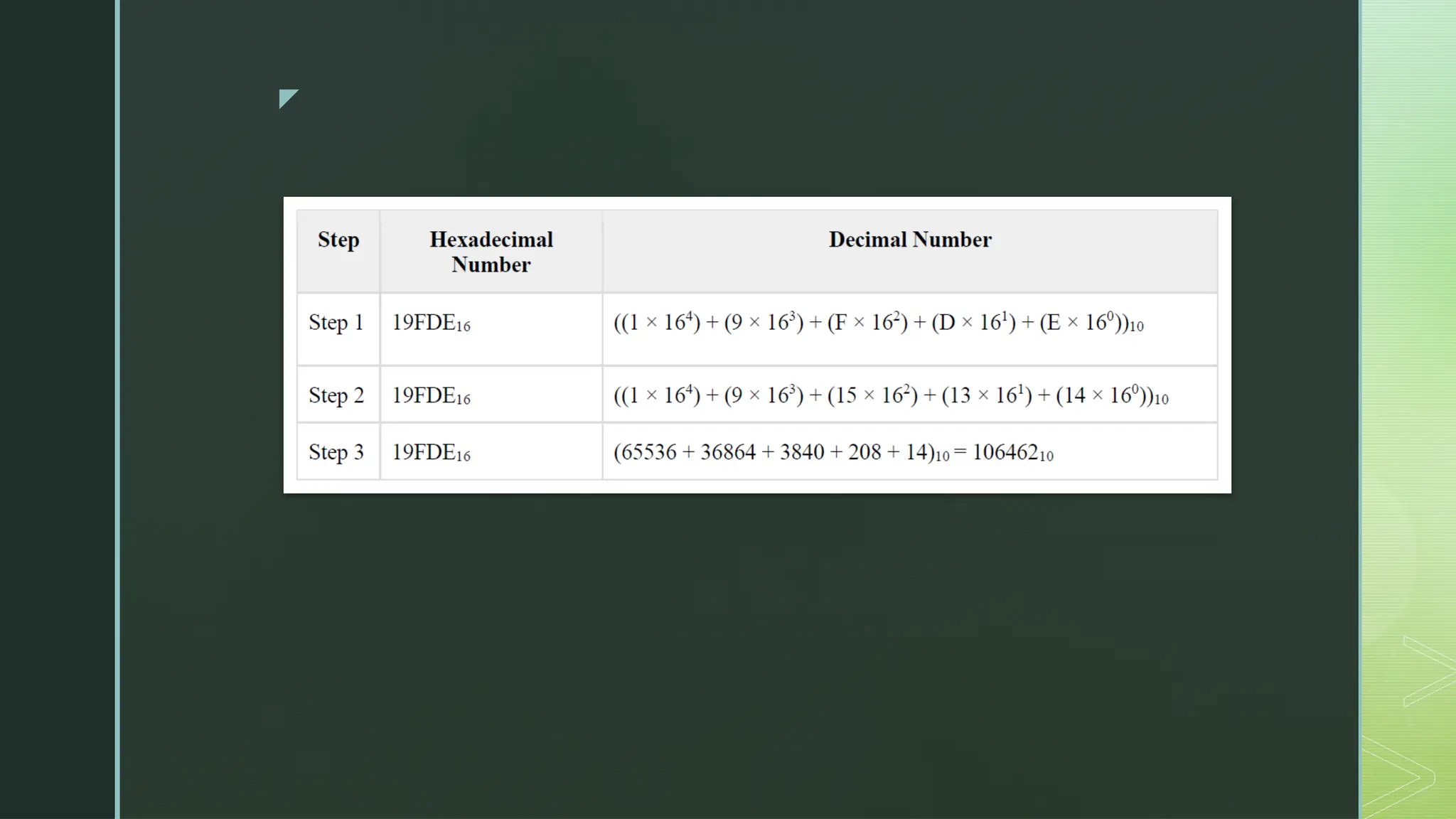
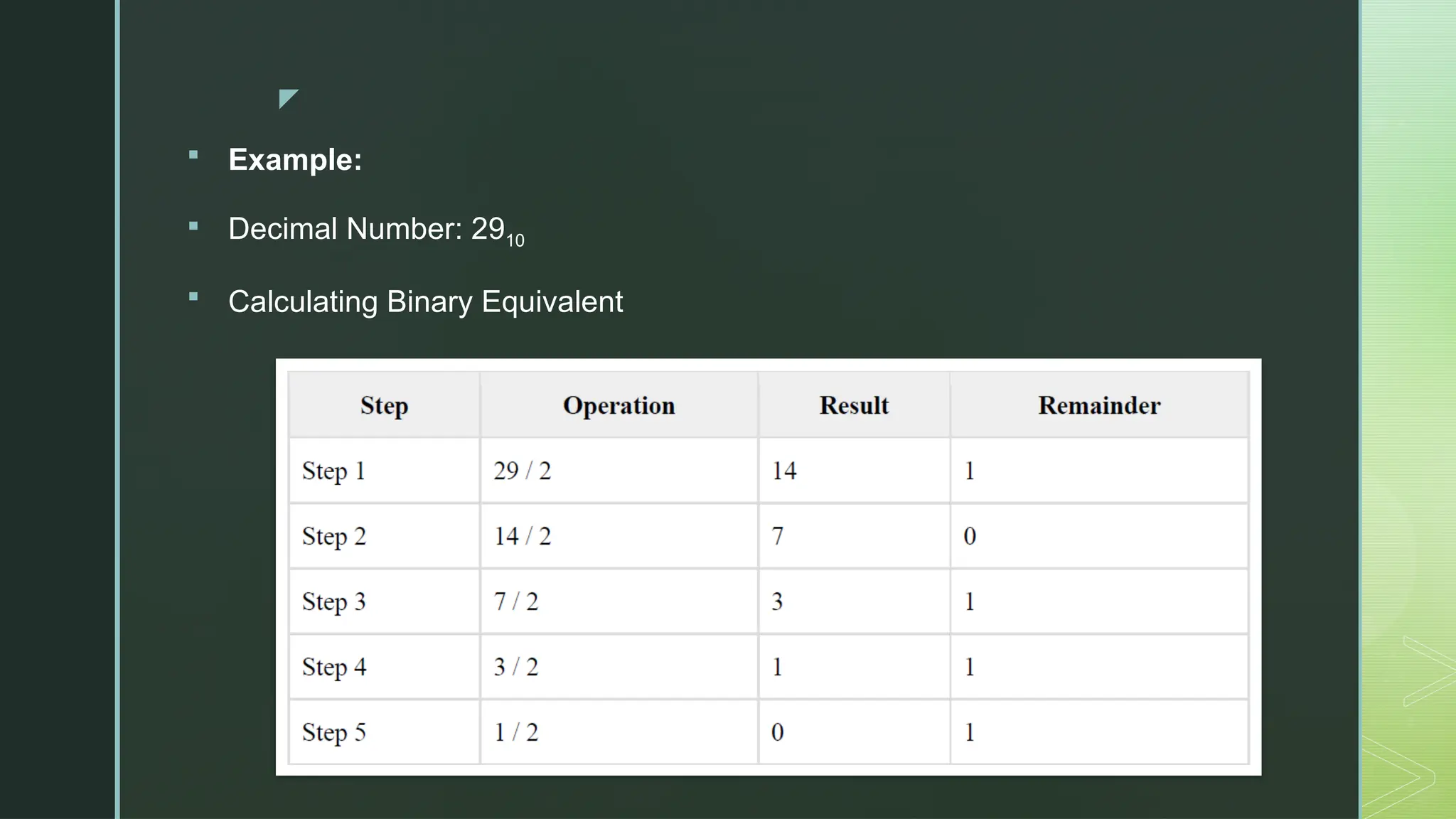
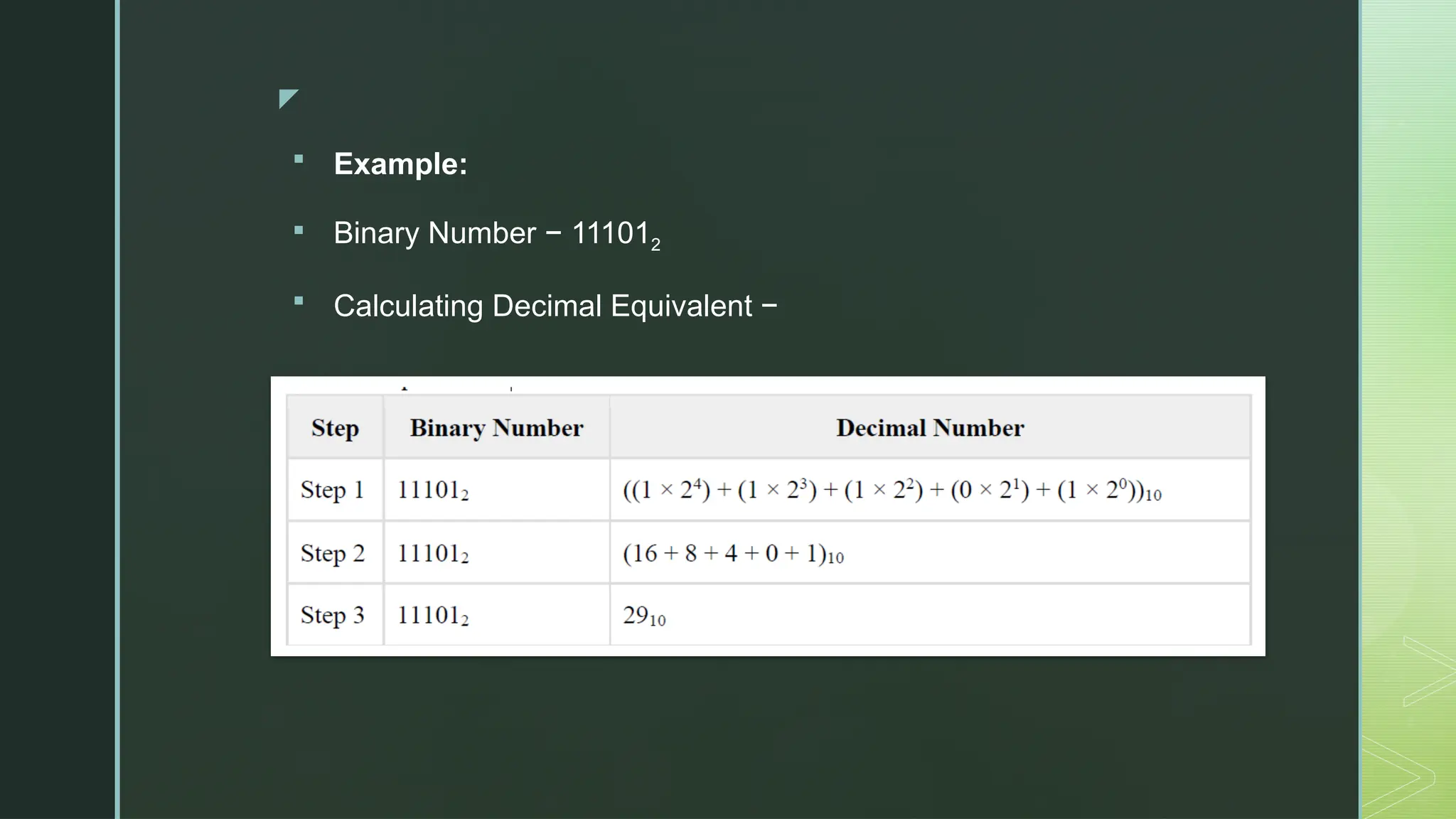
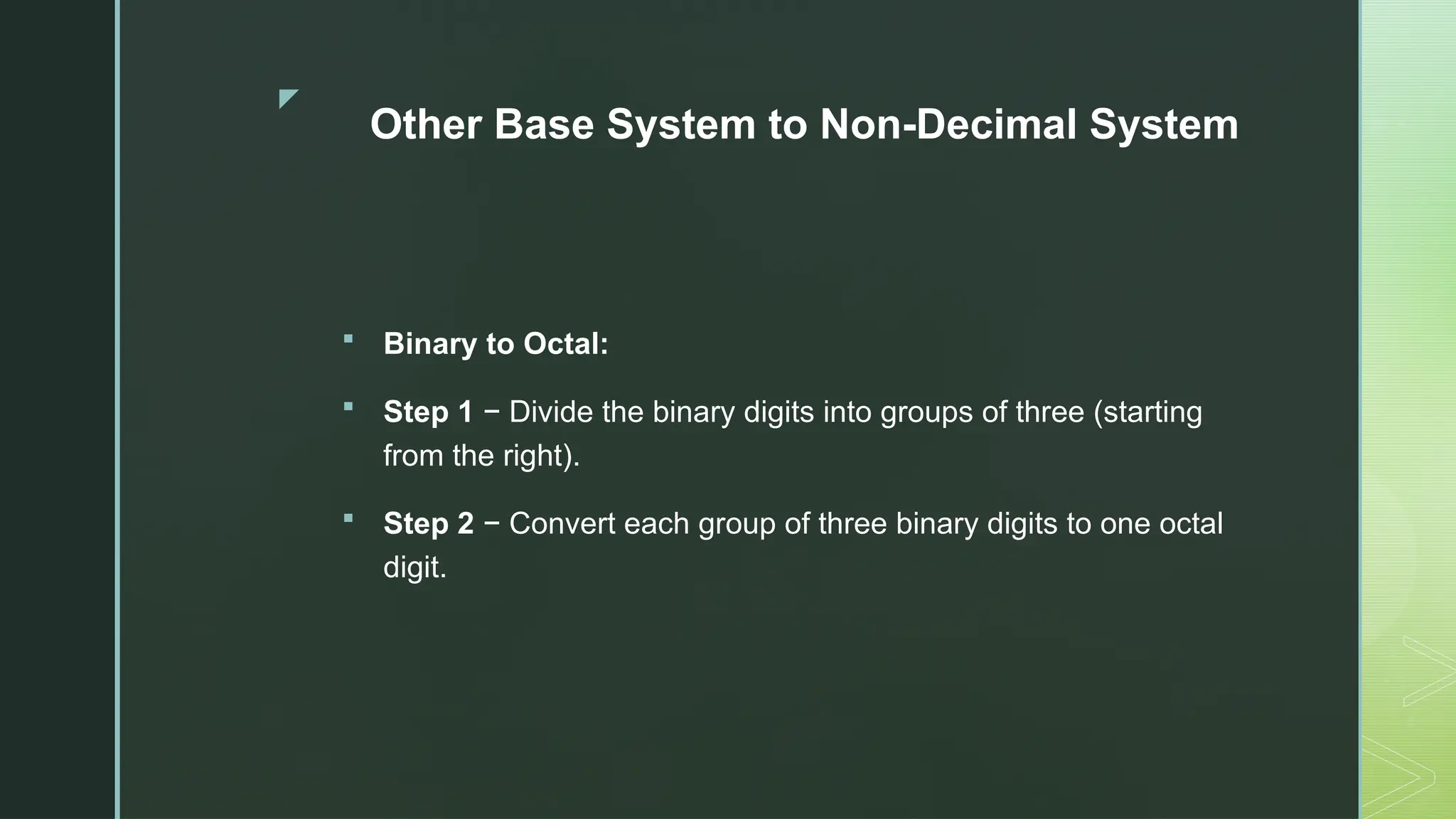
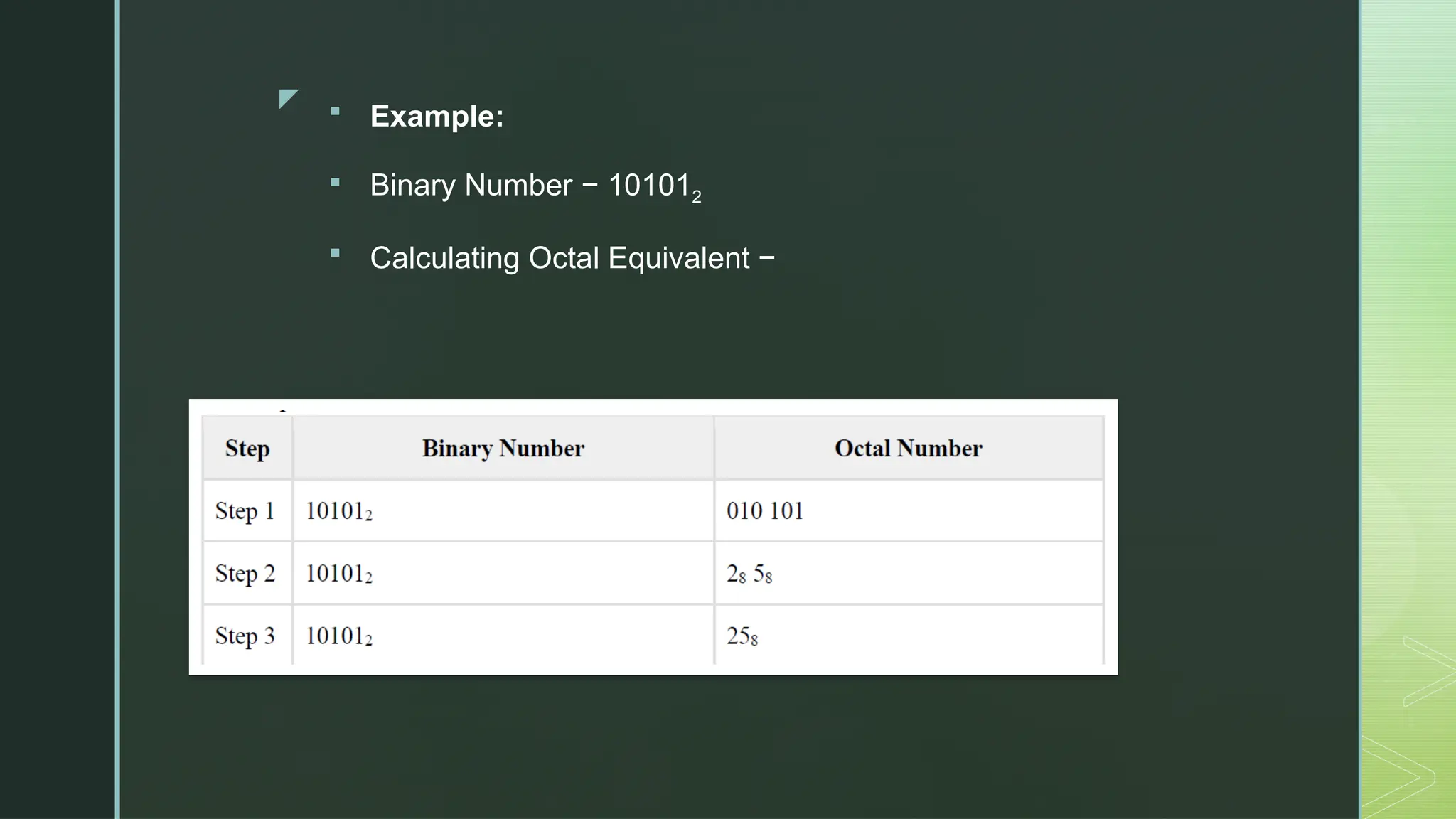
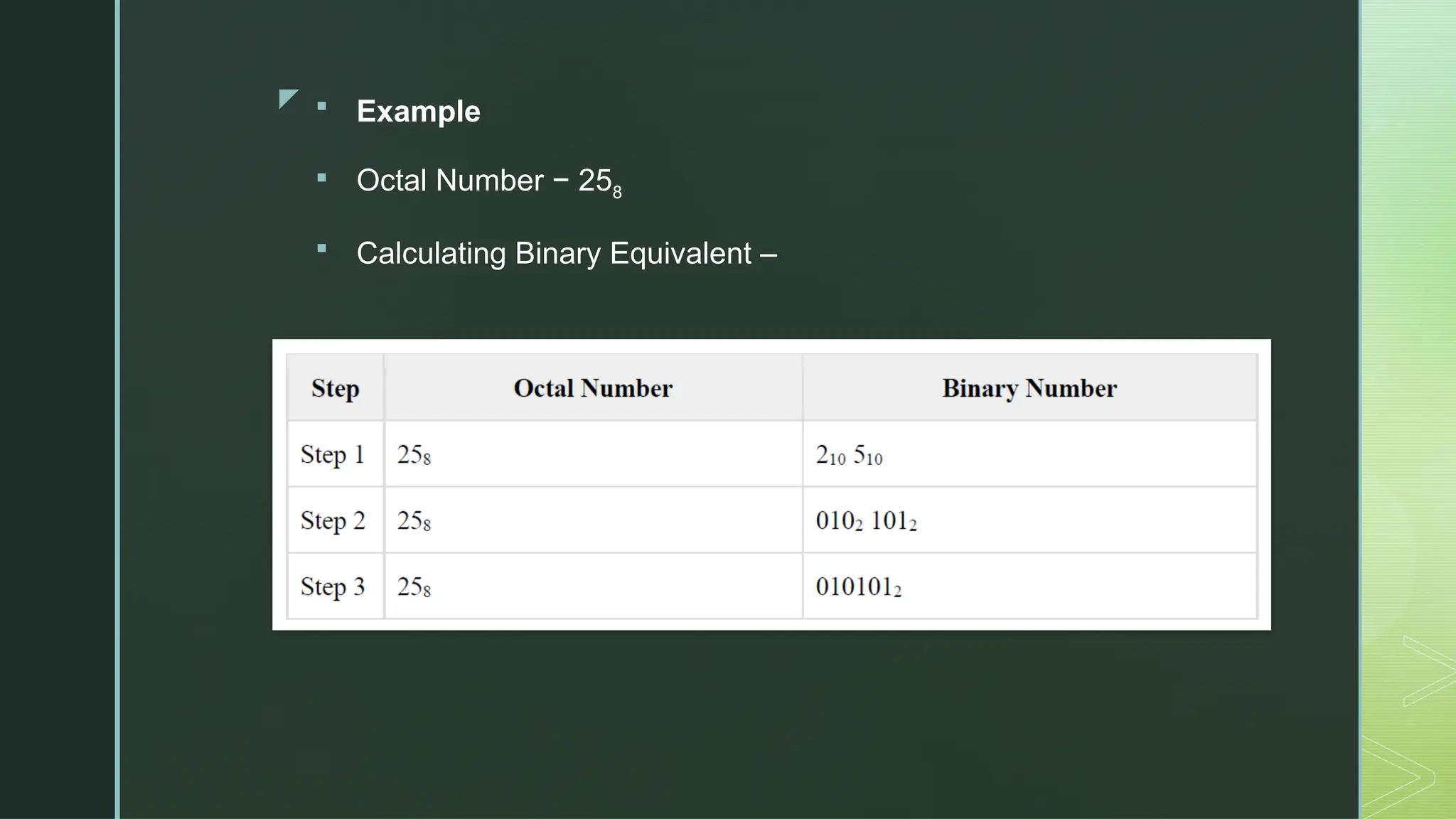
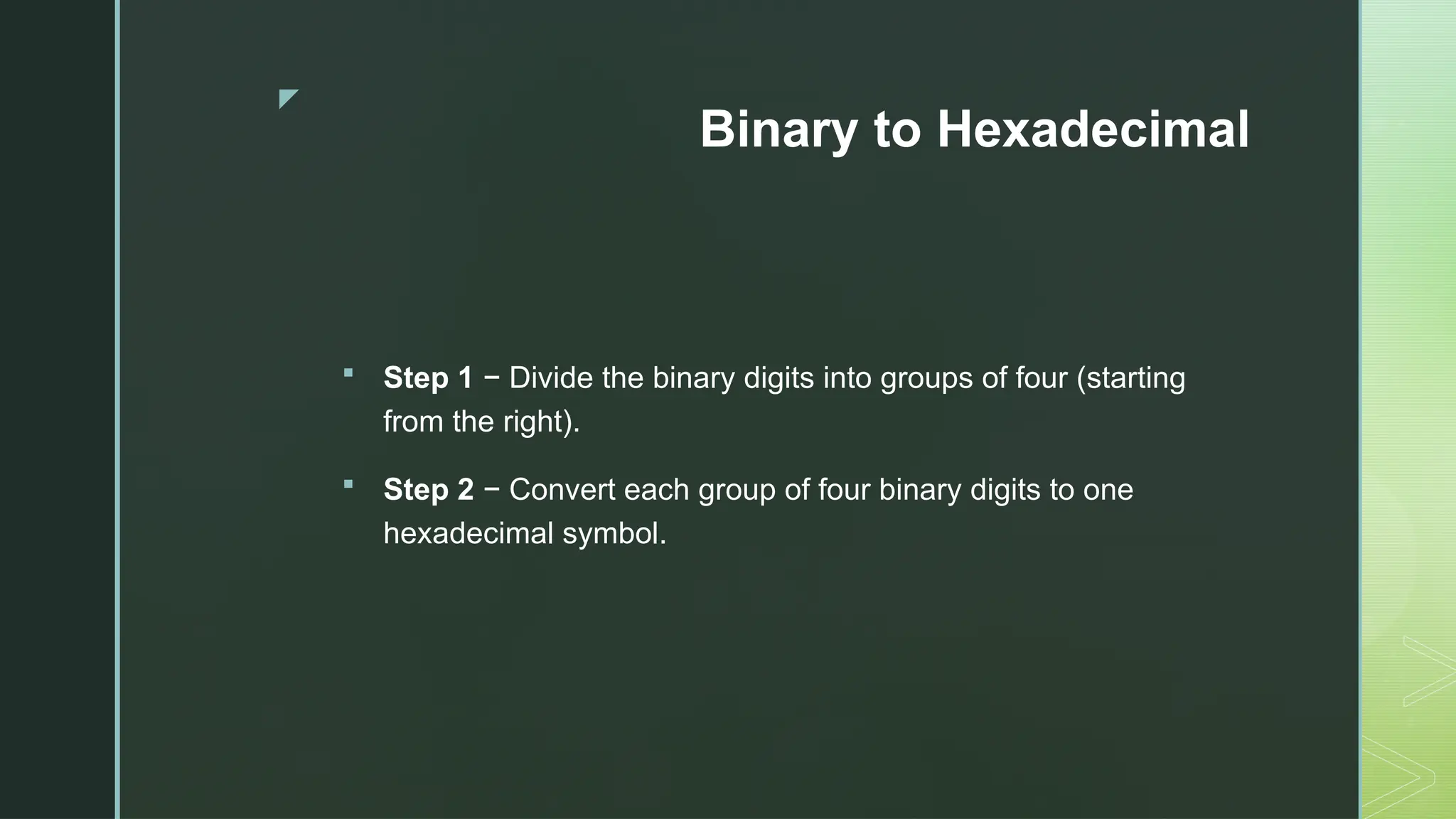
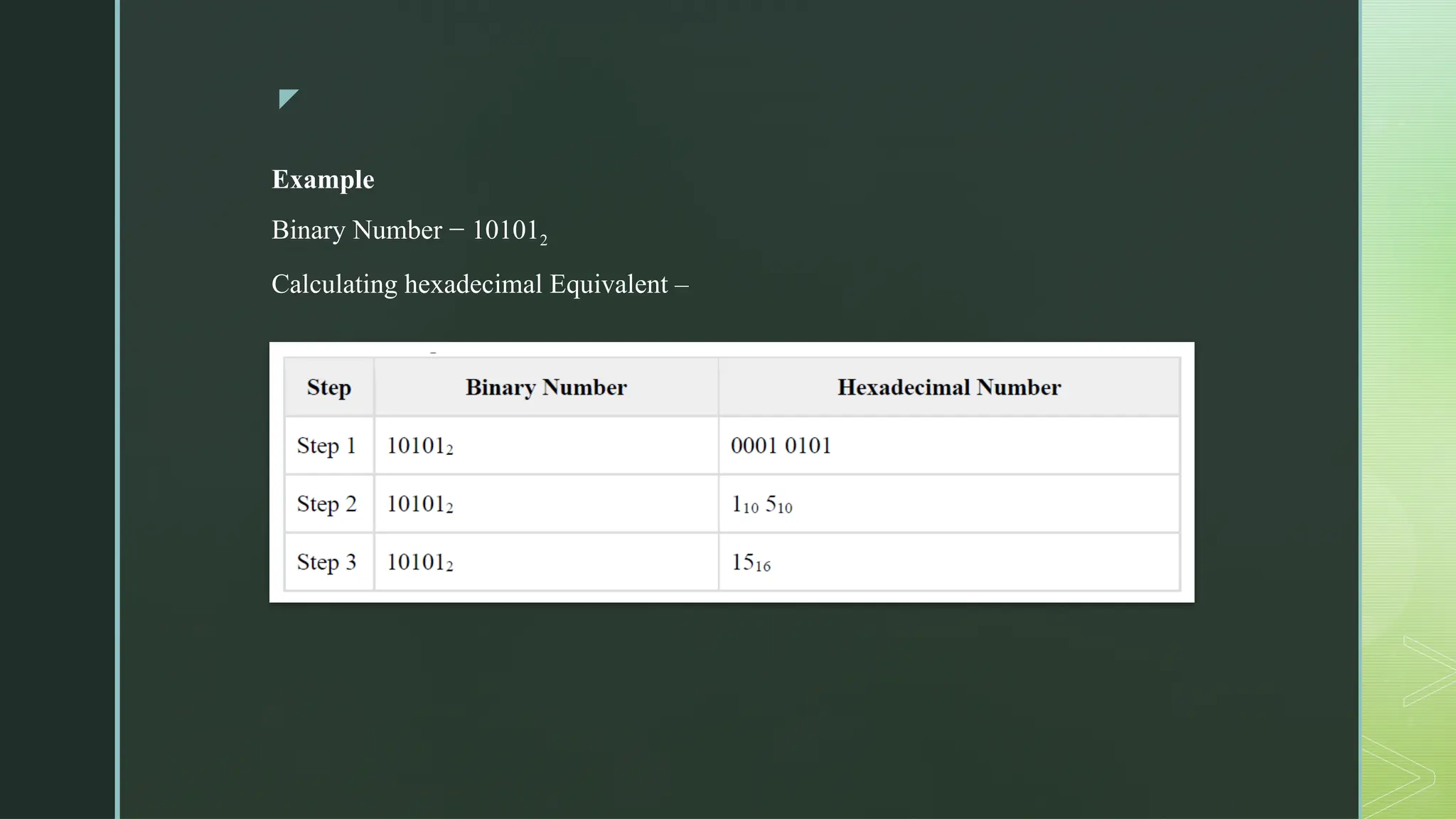
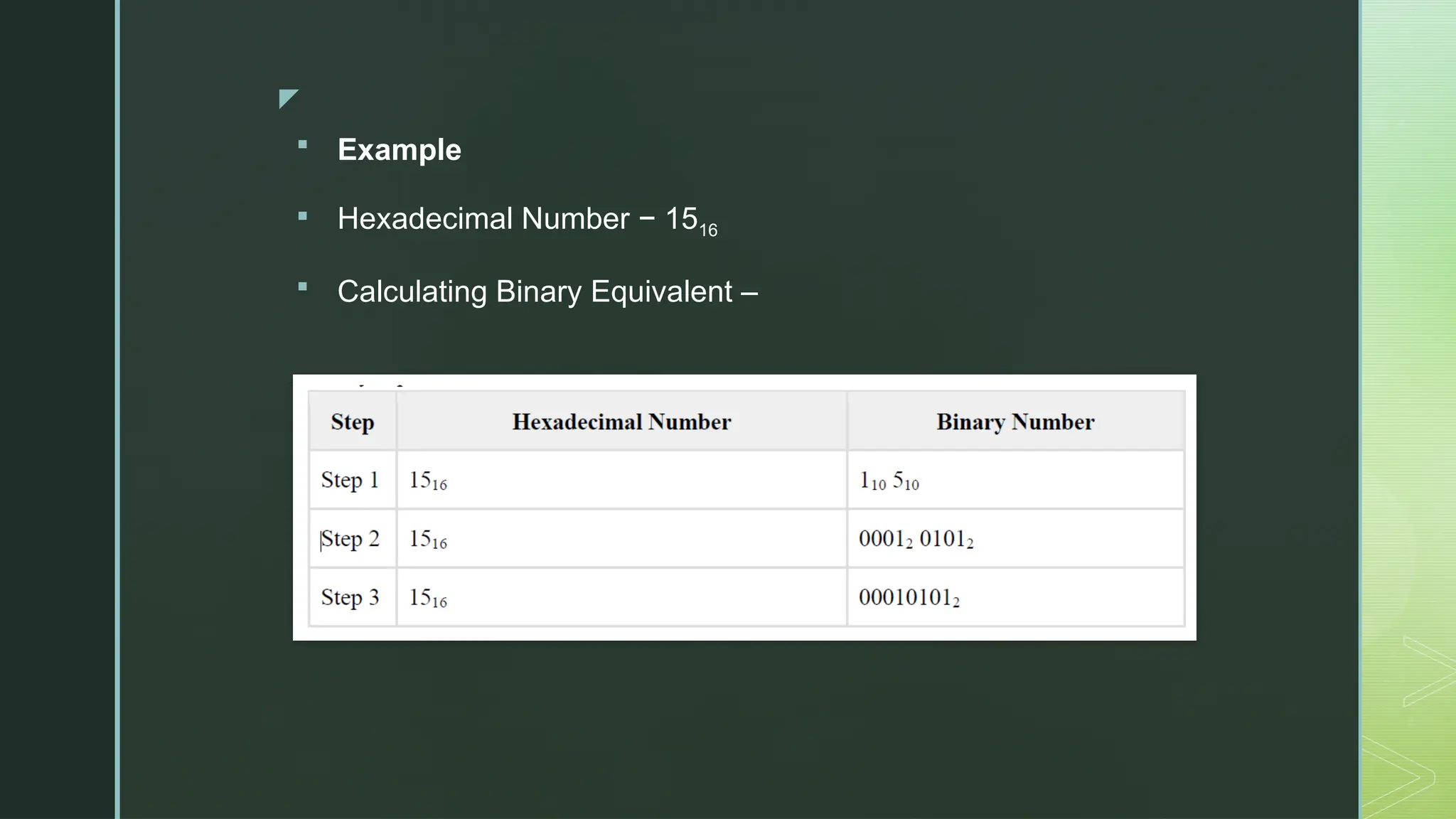
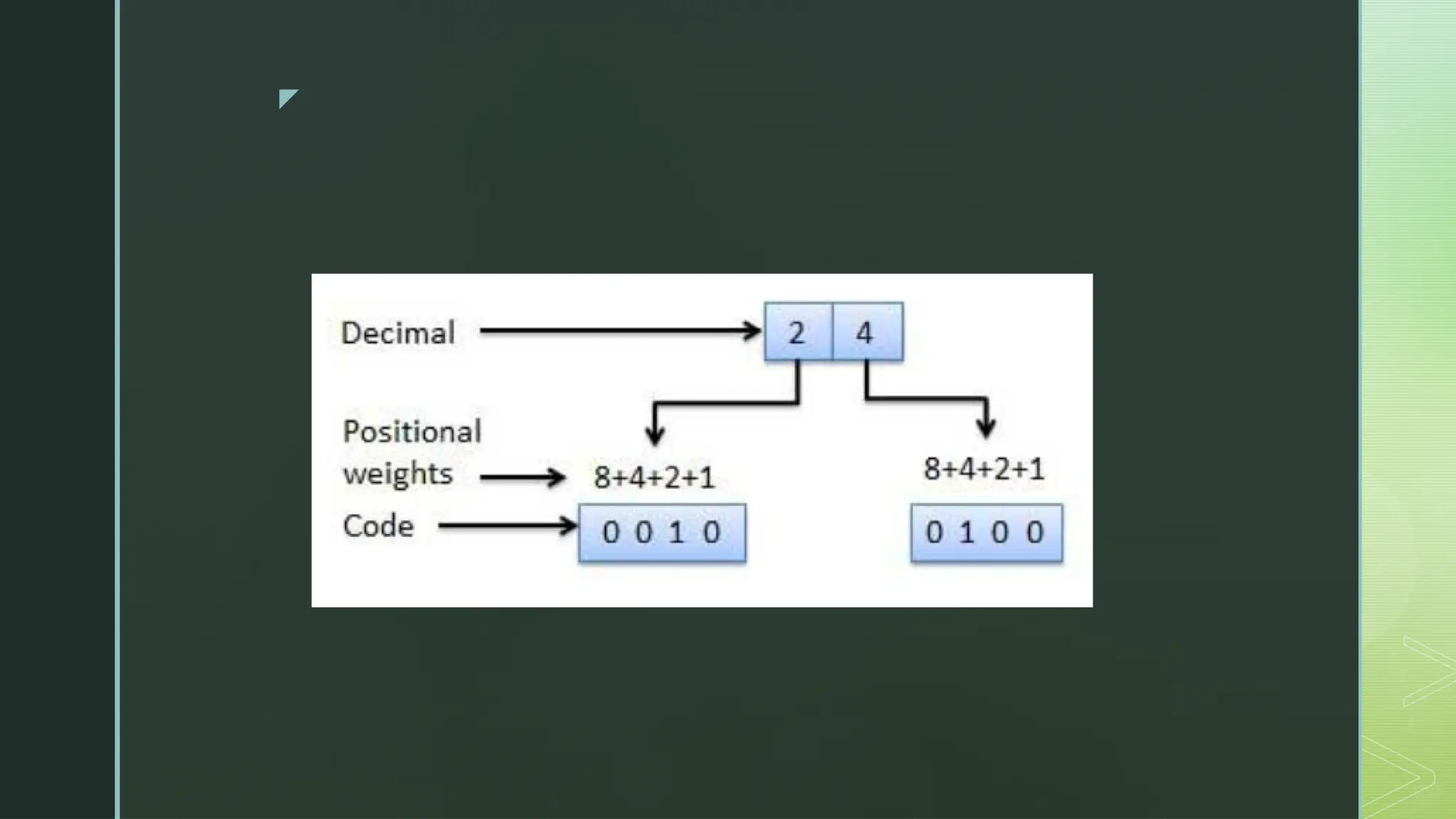
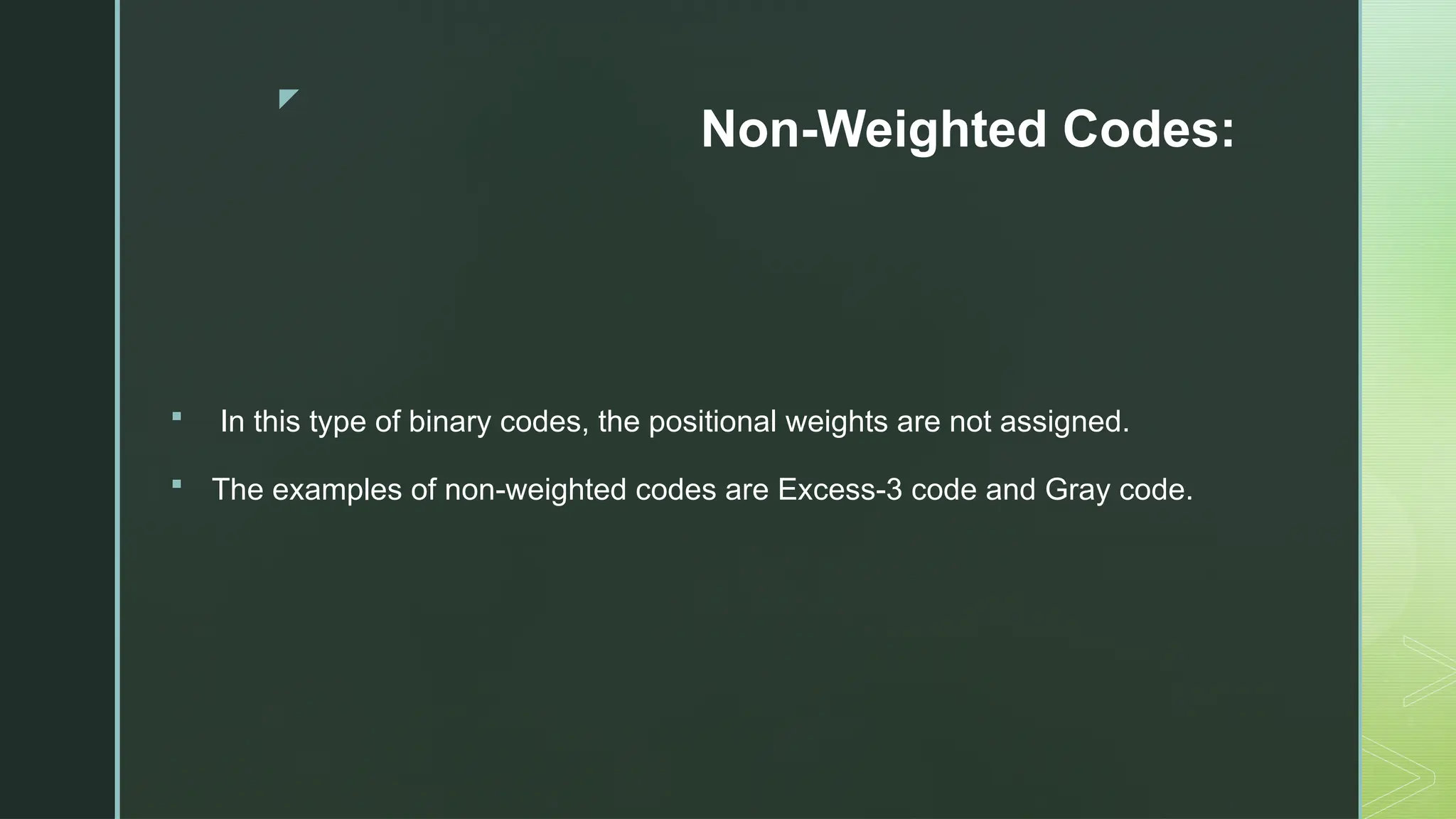
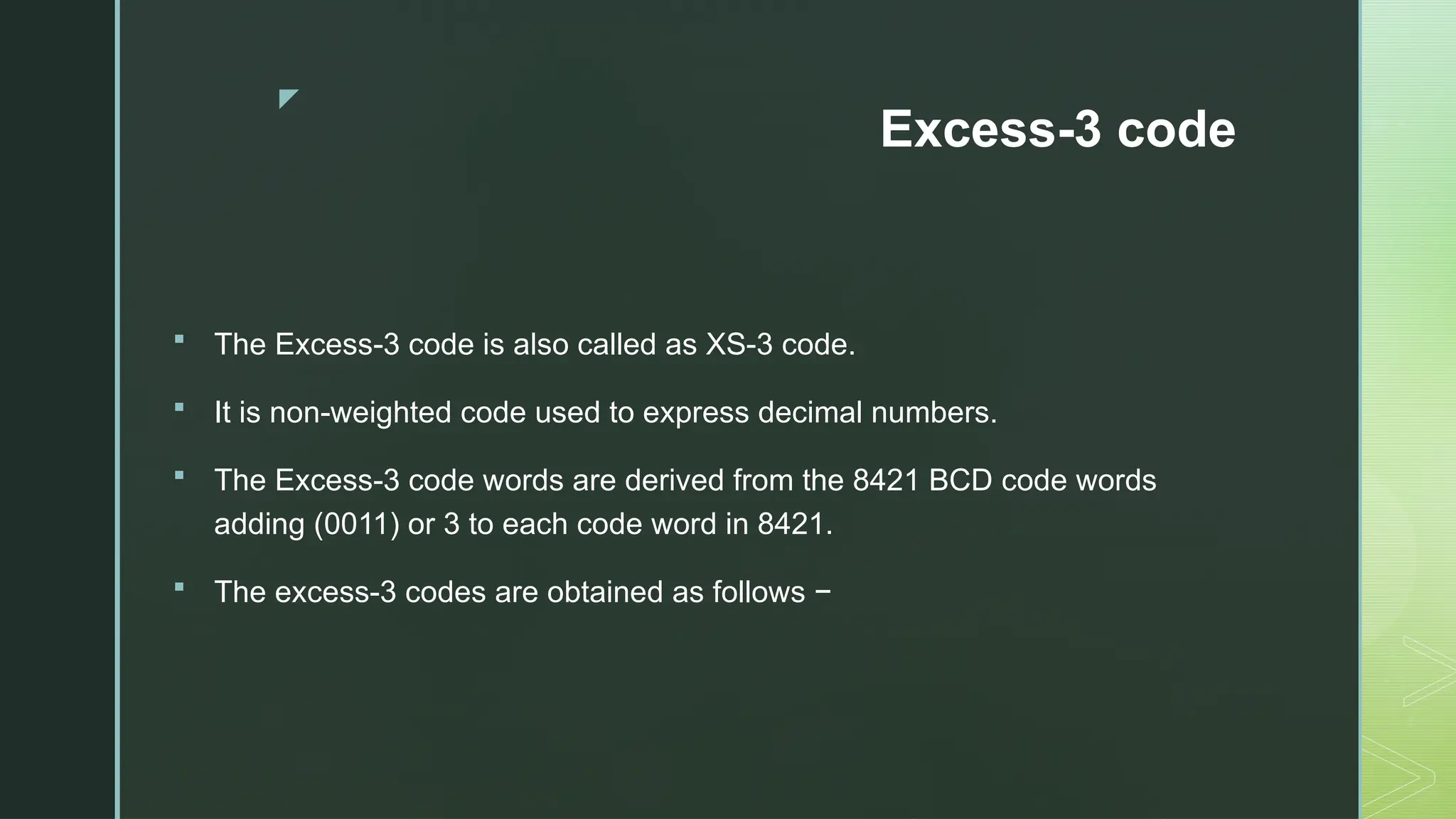
Digital Logic and Computer Architecture are foundational domains in computer science and electronics that enable the design, development, and analysis of digital systems and computing machines. At the heart of digital logic lies the binary number system, which uses only two digits—0 and 1—to represent and process all types of data. Computers rely on binary because digital electronic devices are inherently bistable, meaning they can exist in only two distinct states. Number systems such as binary, octal, decimal, and hexadecimal are crucial for representing data in forms that are easy for both humans and machines to understand. Logic gates—AND, OR, NOT, NAND, NOR, XOR, and XNOR—are the basic building blocks of digital circuits, each performing a specific Boolean function. These gates are combined to form combinational circuits like adders, multiplexers, encoders, and decoders, which produce outputs based solely on current inputs. Boolean algebra and simplification techniques like Karnaugh maps and the Quine-McCluskey method are employed to minimize logical expressions, reducing hardware complexity. Beyond combinational logic, sequential circuits add memory elements to the system. These include flip-flops, registers, and counters, which store past inputs and states, making them essential for timing, control, and memory functions. Flip-flops such as SR, D, JK, and T types are used to build higher-level components, with synchronous and asynchronous counters being critical for time-keeping and control applications. A central theme in digital logic is the representation of data. Computers handle various data types—integers, floating-point numbers, characters, and instructions—using binary encoding. Signed integers are often stored in 2's complement format to simplify arithmetic operations, while floating-point numbers follow the IEEE 754 standard to represent very large or very small values. ASCII and Unicode standards are used to encode characters. Arithmetic operations such as addition, subtraction, multiplication, and division are implemented using specialized algorithms and circuits within the Arithmetic Logic Unit (ALU), a key component of the CPU. The ALU performs both arithmetic and logical functions, serving as the brain of computational tasks. Data transfer among components relies on a well-structured bus system, and memory units form a hierarchy based on speed and size. This hierarchy starts with processor registers, followed by cache memory (L1, L2, L3), main memory (RAM), and secondary storage (hard disks, SSDs), extending to tertiary storage such as optical drives. The goal is to balance cost, speed, and storage capacity. Cache memory significantly improves speed by storing frequently used data and instructions closer to the processor, employing mapping techniques like direct mapping, fully associative mapping, and set-associative mapping. Modern computers often employ multicore processors—multiple CPUs integrated into a single chip—to e

1. z
CSC304 - Digital Logic &
Computer Organization
and Architecture

2. z
Course Overview
 Understand the internal working of digital computers
 Learn binary systems, data operations, memory, and
processor design
 Application in embedded systems, processors, and
digital devices.

3. z
Module 1 – Computer Fundamentals
 Number Systems: Binary, Octal, Decimal, Hexadecimal
 Codes: BCD, Gray, Excess-3, ASCII
 Logic Gates: AND, OR, NOT, NAND, NOR, XOR
 Basic Computer Organization & Von Neumann Model

4. z
Module 2 – Data Representation &
Arithmetic
 Binary Arithmetic: Addition, Subtraction, Multiplication,
Division
 Compliments: 1's and 2's complement methods
 Booth's Multiplication, Restoring & Non-Restoring
Division
 IEEE-754 Floating Point Representation

5. z
Module 3 – Processor Organization
 Adders, MUX, DEMUX, Flip-flops (SR, JK, D, T)
 Instruction Formats, Addressing Modes
 Instruction Cycle: Fetch, Decode, Execute

6. z
Module 4 – Control Unit Design
 Hardwired Control: State table, delay element
methods.
 Microprogrammed Control: Micro-ops, sequencing,
control memory.

7. z
Module 5 – Memory Organization
 RAM, ROM, Cache, Interleaved & Associative Memory
 Memory Hierarchy: Registers → Cache → Main Memory
→ Secondary
 Cache Mapping, Write Policies, Cache Coherence

8. z
Module 6 – Advanced Processor & Buses
 Pipelined Data Path, Hazards, Branch Prediction
 Flynn's Classification: SISD, SIMD, MISD, MIMD
 Buses: ISA, PCI, USB, Contention & Arbitration

9. z
Course Outcomes
 Understand digital number systems and basic
computer structure
 Apply arithmetic algorithms
 Explain processor components and control logic
 Demonstrate memory organization
 Understand multicore concepts and buses

10. z
Number Systems
 Decimal
 Binary
 Octal
 Hexa-decimal

11. z
Introduction to Number System and
Codes
 A number system is a way to represent and
express numbers using a specific set of symbols
(digits) and a base (radix). In computer systems,
number systems are fundamental because
computers operate on binary digits (bits).

12. z
Number
System
Base Digits Used Example
Decimal 10 0–9 459, 82.5
Binary 2 0, 1 1011₂
Octal 8 0–7 745₈
Hexadecimal 16 0–9, A–F 2F , 1A3
₁₆ ₁₆

13. z
Why Do We Use Different Codes in
Digital Systems?
 Digital systems use codes to represent
numbers, characters, and symbols in binary
form. These are called binary codes.

14. z
Code Type Purpose Example
BCD (Binary-Coded
Decimal)
Represents decimal digits in
binary (4 bits per digit)
59 = 0101 1001
Gray Code
Only one-bit changes at a time
(used in encoders to reduce
error)
Binary 3 = 011, Gray = 010
ASCII
Represents text characters in
computers
'A' = 65 = 01000001
Unicode
Extended character set for all
languages
'अ' = U+0905
Excess-3 Code
BCD variant used in error
detection
3 → 0110 (binary 3 + 0011)

15. z
Number Systems: Binary, Octal, Decimal, Hexadecimal
 A digital system can understand positional number system.
 In this system, there are a few symbols called digits which represent different values
depending on the position they occupy in the number.
 A value of each digit in a number can be determined using:
 The digit
 The position of the digit in the number
 The base of the number system (where base is defined as the total number of digits
available in the number system).
 There are different types of number system like binary, decimal, hexadecimal and octal.

16. z
Decimal Number System
 The number system that we use in our day-to-day life is the decimal
number system.
 Decimal number system has base 10 as it uses 10 digits from 0 to 9.
 Each position represents a specific power of the base (10).

17. z
Binary Number System
 Uses two digits, 0 and 1. Also called base 2 number system
 Each position in a binary number represents a power of the base (2). Position
1 in LSB represents 20
 Example: Binary Number: 101012. Calculating Decimal Equivalent –

18. z

19. z
Octal Number System
 Uses eight digits, 0,1,2,3,4,5,6,7.
 Also called base 8 number system
 Each position in an octal number represents a power of the base (8).
Example: Position 1 in LSB represents 80
 Example: Octal Number − 125708
 Calculating Decimal Equivalent –

20. z

21. z
Hexadecimal Number System
 Uses 10 digits and 6 letters, 0,1,2,3,4,5,6,7,8, 9, A, B, C, D, E, F.
 Letters represent numbers starting from 10. A = 10, B = 11, C = 12, D = 13, E
= 14, F = 15.
 Also called base 16 number system.
 Each position in a hexadecimal number represents a power of the base (16).
Example: Position 1 in LSB represents 160
.
 Example: Hexadecimal Number: 19FDE16

22. z

23. z
Number System Conversion
 Decimal to Other Base System
 Other Base System to Decimal
 Other Base System to Non-Decimal
 Binary to Octal
 Octal to Binary
 Binary to Hexadecimal
 Hexadecimal to Binary
 Octal to Hexadecimal
 Hexadecimal to Octal

24. z
Decimal to Other Base System
The steps are as follows:
 Step 1 − Divide the decimal number to be converted by the value of the new
base.
 Step 2 − Get the remainder from Step 1 as the rightmost digit (least
significant digit) of new base number.
 Step 3 − Divide the quotient of the previous divide by the new base.
 Step 4 − Record the remainder from Step 3 as the next digit (to the left) of
the new base number.
 Repeat Steps 3 and 4, getting remainders from right to left, until the quotient
becomes zero in Step 3. The last remainder thus obtained will be the Most
Significant Digit (MSD) of the new base number.

25. z
 Example:
 Decimal Number: 2910
 Calculating Binary Equivalent

26. z
Other Base System to Decimal
System
 The steps are as follows:
 Step 1 − Determine the column (positional) value of each digit
(this depends on the position of the digit and the base of the
number system).
 Step 2 − Multiply the obtained column values (in Step 1) by the
digits in the corresponding columns.
 Step 3 − Sum the products calculated in Step 2. The total is the
equivalent value in decimal.

27. z
 Example:
 Binary Number − 111012
 Calculating Decimal Equivalent −

28. z
Other Base System to Non-Decimal System
 Binary to Octal:
 Step 1 − Divide the binary digits into groups of three (starting
from the right).
 Step 2 − Convert each group of three binary digits to one octal
digit.

29. z  Example:
 Binary Number − 101012
 Calculating Octal Equivalent −

30. z
Octal to Binary
 Step 1 − Convert each octal digit to a 3-digit binary number (the
octal digits may be treated as decimal for this conversion).
 Step 2 − Combine all the resulting binary groups (of 3 digits
each) into a single binary number.

31. z  Example
 Octal Number − 258
 Calculating Binary Equivalent –

32. z
Binary to Hexadecimal
 Step 1 − Divide the binary digits into groups of four (starting
from the right).
 Step 2 − Convert each group of four binary digits to one
hexadecimal symbol.

33. z
Example
Binary Number − 101012
Calculating hexadecimal Equivalent –

34. z
Hexadecimal to Binary
 Step 1 − Convert each hexadecimal digit to a 4-digit binary
number (the hexadecimal digits may be treated as decimal for
this conversion).
 Step 2 − Combine all the resulting binary groups (of 4 digits
each) into a single binary number.

35. z
 Example
 Hexadecimal Number − 1516
 Calculating Binary Equivalent –

36. z
 Octal (Base-8) and Hexadecimal (Base-16) are both number systems
used for compact binary representation. While they don’t convert
directly, we use Binary as an intermediate step for accurate conversion.
 Why Use Binary as an Intermediate?
 Octal → Binary: Each digit = 3 bits
 Hex → Binary: Each digit = 4 bits
 So, we convert:
 Octal → Binary → Hexadecimal
 Hexadecimal → Binary → Octal

37. z
Octal to Hexadecimal
Steps:
 Convert each octal digit to 3-bit binary.
 Combine all binary groups.
 Regroup binary into 4-bit chunks (from right).
 Convert each 4-bit binary to hex digit.

38. z
Example: Convert (735) to Hex
₈ .
 Step 1: Octal → Binary
7 → 111
3 → 011
5 → 101
So, (735) = 111 011 101 (binary)
₈
 Step 2: Group 4 bits from right → 1 1101 1101
Pad with 0s on left: 0001 1101 1101
 Step 3: Binary → Hex
0001 → 1
1101 → D
1101 → D
 Final Answer: (735) = (1DD)
₈ ₁₆

39. z
Hexadecimal to Octal
Steps:
 Convert each hex digit to 4-bit binary.
 Combine all binary groups.
 Regroup binary into 3-bit chunks (from right).
 Convert each 3-bit group to octal digit.

40. z  Example: Convert (2F)16 to Octal
 Step 1: Hex → Binary
2 → 0010
F → 1111
So, (2F) = 0010 1111
₁₆
 Step 2: Group in 3 bits (from right): 00 101 111
Pad left if needed: 000 101 111
 Step 3: Binary → Octal
000 → 0
101 → 5
111 → 7
 Final Answer: (2F)16 = (057)8

41. z
Octal Addition
 Start from the rightmost column: Add the
digits in each column.
 If the sum is less than or equal to
7: Write the sum directly below.
 If the sum is greater than 7:
 Subtract 8 from the sum.
 Write the result below.
 Carry-over a 1 to the next column.

42. z
Octal Subtraction
 Start from the rightmost column: Subtract the
bottom digit from the top digit.
 If the top digit is smaller than the bottom digit:
 Borrow 8 from the next column.
 Add 8 to the top digit.
 Subtract the bottom digit.

43. z
Codes: Grey, BCD, Excess-3, ASCII

44. z
Binary Codes
 In the coding, when numbers, letters or words are represented by a specific group
of symbols, it is said that the number, letter or word is being encoded.
 The group of symbols is called as a code.
 The digital data is represented, stored and transmitted as group of binary bits.
 This group is also called as binary code.
 The binary code is represented by the number as well as alphanumeric letter.

45. z
Advantages of Binary Code
 Binary codes are suitable for the computer applications.
 Binary codes are suitable for the digital communications.
 Binary codes make the analysis and designing of digital circuits if we use the
binary codes.
 Since only 0 & 1 are being used, implementation becomes easy.

46. z
Classification of binary codes
The codes are broadly categorized into following four categories.
 Weighted Codes
 Non-Weighted Codes
 Binary Coded Decimal Code

47. z
Weighted Codes
 Weighted binary codes are those binary codes which obey the positional weight
principle.
• Each position of the number represents a specific weight.
• Several systems of the codes are used to express the decimal digits 0 through 9.
• In these codes each decimal digit is represented by a group of four bits.

48. z

49. z
Non-Weighted Codes:
 In this type of binary codes, the positional weights are not assigned.
 The examples of non-weighted codes are Excess-3 code and Gray code.

50. z
Excess-3 code
 The Excess-3 code is also called as XS-3 code.
 It is non-weighted code used to express decimal numbers.
 The Excess-3 code words are derived from the 8421 BCD code words
adding (0011) or 3 to each code word in 8421.
 The excess-3 codes are obtained as follows −

51. z
Gray Code
 It is the non-weighted code. That means there are no specific weights assigned to
the bit position.
 It has a very special feature that, only one bit will change each time the decimal
number is incremented.
 As only one-bit changes at a time, the gray code is called as a unit distance code.
 The gray code is a cyclic code.
 Gray code cannot be used for arithmetic operation.

52. z
Procedure to calculate Gray Code of
a Binary Number:
 The MSB (Most Significant Bit) of the gray code will be exactly equal to the first bit of the
given binary number.
 The second bit of the code will be exclusive-or (XOR) of the first and second bit of the
given binary number, i.e. if both the bits are same the result will be 0 and if they are
different the result will be 1.
 The third bit of gray code will be equal to the exclusive-or (XOR) of the second and third
bit of the given binary number. Thus, the binary to gray code conversion goes on. An
example is given below to illustrate these steps.
 In simple language: Start from left, copy MSB. Check adjacent digits one by one, If
same-> 0, Different->1.

53. z
Application of Gray code:
Gray code is popularly used in the shaft position encoders.

54. z
Binary Coded Decimal (BCD) code:
 In this code each decimal digit is represented by a 4-bit binary number.
 BCD is a way to express each of the decimal digits with a binary code.
 In the BCD, with four bits we can represent sixteen numbers (0000 to
1111).
 But in BCD code only first ten of these are used (0000 to 1001).
 The remaining six code combinations i.e. 1010 to 1111 are invalid in BCD.

55. z
Advantages of BCD Codes:
• It is very similar to decimal system.
• We need to remember binary equivalent of decimal numbers 0 to 9 only.
Disadvantages of BCD Codes:
• The addition and subtraction of BCD have different rules.
• The BCD arithmetic is little more complicated.
• BCD needs a greater number of bits than binary to represent the decimal
number. So, BCD is less efficient than binary.