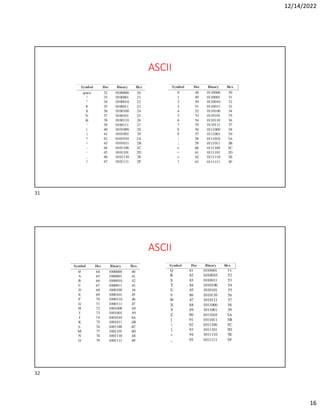
Hexadecimal is a base-16 number system used to compactly represent binary numbers. It uses 16 symbols - 0-9 and A-F. Counting proceeds from F to 10, then 20, etc. Binary numbers can be converted to and from hexadecimal by grouping bits into 4-bit blocks and replacing with the hex symbol. Decimal can also be converted to and from hexadecimal using multiplication/division by 16 or remainders. Hexadecimal addition follows decimal addition rules, carrying when sums exceed 15. Octal is base-8 and uses 0-7 symbols, with binary conversion replacing octal digits with 3-bit groups. Binary Coded Decimal represents each decimal digit with 4 bits for easy decimal interfacing. Gray code changes

1. 12/14/2022
1
Logic Circuits Design
Lecture 2
Dr. Rand Ali
Hexadecimal Numbers
• The hexadecimal number system has a base of 16; that it is composed
of 16 numeric (0-9 digits) and alphabetic (A-F letters) characters.
• It is used primarily as a compact way of displaying or writing binary
numbers because it is very easy to convert between binary and
hexadecimal.
• Each hexadecimal digit represents a 4-bit binary number
1
2

2. 12/14/2022
2
Counting in Hexadecimal Numbers
Count in hexadecimal once you get to F by starting over with
another column and continue as follow:
With two hexadecimal digits, you can count up to FF16 .
To count beyond FF16 , three hexadecimal digital are needed
where the maximum 3-digit hexadecimal number is FFF16.
Binary-to-Hexadecimal Conversion
• To convert a binary number to a hexadecimal, break the binary
number into 4-bit groups. Then, starting at the right-most bit and
replace each 4-bit group with equivalent hexadecimal symbol.
Example: Convert the following binary numbers to hexadecimal:
a) 1100101001010111 b)111111000101101001
Solution:
note: two zeros have been added in
(b) to complete a 4-bit group at
the left
3
4

3. 12/14/2022
3
Hexadecimal to Binary Conversion
• To convert from a hexadecimal number to binary number, replace
each hexadecimal symbol with the corresponding four bits.
• Example: Determine the binary numbers for the following
hexadecimal numbers:
• a) 10A416 b)CF8E16 c)3A6.C
Solution:
(c)
Hexadecimal-to-Decimal-Conversion
• Method1: Convert the hexadecimal number to binary number and
then convert from binary to decimal.
• Example: Convert the following hexadecimal numbers to decimal:
a)1C16 b)A8516
5
6

4. 12/14/2022
4
Hexadecimal-to-Decimal-Conversion
Method2: Multiply the decimal value of each hexadecimal digit by its weight and
then take the sum of these product.
• The weights of a hexadecimal number are increasing powers of 16 from right to
left).
• Example: Convert the following hexadecimal numbers to decimal:
(a) E516 (b)B2F816
Solution:
Decimal-to-Hexadecimal Conversion
• Repeated division of a decimal number by 16 will produce the equivalent
hexadecimal number, formed by the remainders of the divisions.
• The first remainder produced is the least significant bit (LSB).
• Each successive division by 16 produces a remainder that that becomes a digit in
the equivalent hexadecimal number.
Example: Convert the decimal number 650 to hexadecimal
7
8

5. 12/14/2022
5
Hexadecimal Addition
When adding two hexadecimal values, use the following rules:
1- In any given column of an addition problem, think of the two hexadecimal digits in
terms of their decimal values. For example, 516 = 510 , A16 = 1010.
2-If the sum of these two digits ≤ 1510 , bring down the corresponding hexadecimal digit.
3-If the sum of these two digits > 1510 , bring down the amount of the sum that exceeds
1610 and carry a 1 to the next column.
Example: Add the following hexadecimal numbers: (a) 2B16 + 8416 , (b) DF16 + AC16
Solution:
(a) (b)
Getting the 2’s complement of a hexadecimal number
• There are three methods to get the 2’s complement of a hexadecimal
number. Method 1 is the most common, while the other methods are
alternatives.
• Method1: Convert the hexadecimal number to binary. Then, take the
2’s complement of the binary number, and convert the result to
hexadecimal.
9
10

6. 12/14/2022
6
Getting the 2’s complement of a hexadecimal number
Method2
Method2: Subtract the hexadecimal number from the maximum
hexadecimal number and add 1.
Getting the 2’s complement of a hexadecimal number
Method3
• Method3: Write the sequence of single hexadecimal digits. Then,
write the sequence in reverse below the forward sequence. The 1’s
complement of each hex digit is the digit directly below it; add 1 to
the resulting number to get the 2’s complement.
11
12

7. 12/14/2022
7
Hexadecimal Subtraction
• The 2’s complement allows you to subtract by adding numbers.
• Example: Subtract the following hexadecimal numbers:
a) 8416 – 2A16 b)C316-0B16
Octal Numbers
• The octal number system provides a convenient way to express binary
numbers and codes.
• The octal number system is used less frequently than hexadecimal in
conjunction with computers and microprocessors to express binary
quantities for input and output purposes.
• The octal number system consists of eight digits, which are
0,1,2,3,4,5,6,7
• To count above 7, begin another column and start over:
10, 11, 12, 13, 14, 15, 16, 17, 20, 21, …
• Sometimes, you may see an “o” or a “Q” following an octal number.
13
14

8. 12/14/2022
8
Octal-to-Decimal Conversion
• The evaluation of an octal number in term of its decimal equivalent is
accomplished by multiplying each digit by its weight and summing the
products.
• Example: Convert the octal number 23748 to decimal.
• Solution:
Decimal-to-Octal Conversion
• A method to convert a decimal number to an octal number is the repeated division by 8 method.
• Each successive division by 8 provides a remainder that becomes a digit in the equivalent octal
number
• Example: Convert the decimal number 35910 to octal.
• Solution:
15
16

9. 12/14/2022
9
Octal-to-Binary Conversion
• Each octal digit is represented by three bits as shown below
• To convert an octal number to a binary number, replace each octal digit with appropriate three
bits.
• Example: Convert 75268 to binary
Solution:
Binary-to-Octal Conversion
• To convert a binary number to an octal number, start with right-most
group of three bits and, moving from right to left, convert each 3-bit
group to the equivalent octal digit.
• Example: Convert each of the following binary numbers to octal:
(a) 100110011010 (b) 11010000100
Solution:
17
18

10. 12/14/2022
10
Binary Coded Decimal
• Binary coded Decimal BCD means that each decimal digit, 0 through 9, is represented by a binary
code of four bits.
• We like to read and write in decimal. Therefore, the BCD code provides an excellent interface to
binary systems.
The 8421 BCD Code
• The 8421 is a type of BCD code
• 8421 indicates the binary weights of the four bits (23,22,21,20)
• The main advantage of this code is the ease of the conversion between 8421 code number and
the decimal numbers
• When we refer to BCD, we always mean 8421 code unless otherwise stated
Decimal-to-BCD conversion
• To express any decimal number in BCD, replace each decimal digit
with the appropriate 4-bit code.
• Example: Convert the decimal number 2469 to BCD.
• Solution:
19
20

11. 12/14/2022
11
BCD-to-Decimal Conversion
• To determine a decimal number from a BCD, start at the right most bit
and break the code into groups of four bits. Then write the decimal
digit represented by each 4-bit group.
Example: Convert the BCD code 1001010001110000 to decimal
Solution:
Different Binary codes for the Decimal digits
21
22

12. 12/14/2022
12
Digital Codes
Many specialized codes are used in digital systems such as the Gray
code and the ASCII code.
Gray Code:
• The Gray code is unweighted (no specific weights assigned to the bit
positions)
• It is not an arithmetic code
• It exhibits only a single bit change from one word to the next in
sequence
• The Gray code can have any number of bits
Gray Code
• The table below lists 4-bit Gray code for decimal numbers 0 through
15
23
24

13. 12/14/2022
13
Binary-to-Gray code conversion
• To convert a binary number to a Gray code word, follow the rules
below:
1. The most significant bit (MSB) in the Gray code is the same as the
corresponding MSB in the binary number.
2. Going from left to right, add each adjacent pair of binary code bits
to get the next Gray code bit. Discard carries.
Example: Convert the binary number 10110 to Gray code
Solution: The Gray code is 11101
Gray-to-Binary code conversion
• To convert a Gray code word to binary number, follow the rules
below:
1. The most significant bit (MSB) in the binary number is the same as
the corresponding MSB in the Gray code.
2. Add each binary code bit generated to the Gray code bit in the next
adjacent position. Discard carries.
Example: convert the Gray code 10101111 to binary.
Solution: The binary code is 11001010
25
26

14. 12/14/2022
14
Alphanumeric code
• Alphanumeric codes are codes that represent numbers and
alphabetic characters (letters).
• Also most of the alphanumeric codes represent other characters such
as symbols and various instructions necessary for conveying
information.
• The ASCII is a common alphanumeric code
• ASCII is the abbreviation for American Standard Code for Information
Interchange
• ASCII is a universally accepted alphanumeric code used in most
computers and other electronic equipment
• Most computer keyboards are standardized with ASCII
Alphanumeric code
ASCII
• ASCII has 128 characters and symbols represented by 7-bit binary
code.
• ASCII can be considered as 8-bit code with MSB equals 0; this 8-bit
code is 00 through 7F in hexadecimal.
• The first thirty-two ASCII characters are nongraphic commands (never
printed or displayed) and are used only for control purposes. An
example of the control characters is “escape.”
• The other characters are graphic symbols (can be printed or
displayed) and include the letters of the alphabet (lowercase and
uppercase), the ten decimal digits, punctuation signs, and other
commonly used symbols.
27
28

15. 12/14/2022
15
Alphanumeric code
ASCII
• Example: Determine the binary ASCII codes that are entered from the
computer’s keyboard when the following C ++ language program
statement is typed in.
if (x>5)
Also, express each code in hexadecimal.
Solution:
ASCII
29
30

16. 12/14/2022
16
ASCII
ASCII
31
32

17. 12/14/2022
17
ASCII
33