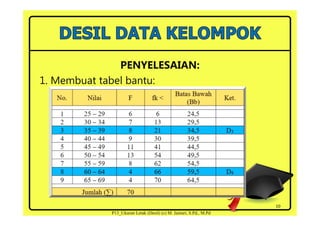
Dokumen ini menjelaskan konsep desil sebagai ukuran letak yang membagi distribusi data menjadi sepuluh bagian yang sama. Terdapat prosedur untuk menghitung desil dari data tunggal dan kelompok, termasuk contoh aplikasi pada hasil ujian mahasiswa dan data nilai siswa. Beberapa rumus dan langkah penyelesaian untuk menentukan nilai desil ke-2, ke-5, dan ke-7 juga disertakan.