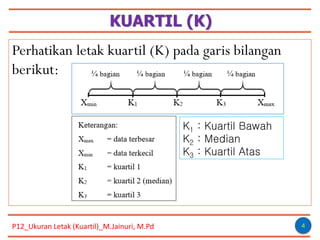
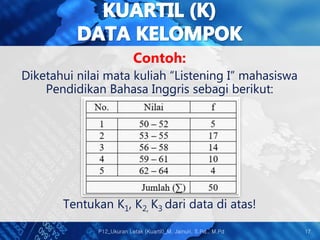
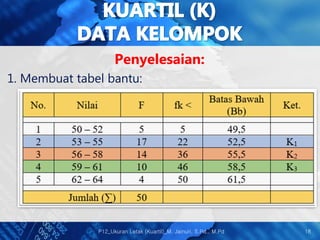
Dokumen tersebut membahas tentang ukuran letak/posisi data, khususnya mengenai kuartil. Kuartil membagi distribusi data menjadi empat bagian yang sama. Dokumen menjelaskan cara menghitung nilai kuartil pertama, kedua, dan ketiga baik untuk data tunggal maupun kelompok beserta contoh penerapannya. [/ringkasan]

1. UKURAN LETAK/POSISI DATA
(Kuartil)
M. Jainuri, S.Pd., M.Pd
1
Pertemuan Ke-12

2. UKURAN LETAK/POSISI DATA
2
Ukuran letak:
merupakan letak/ posisi suatu ukuran
dalam distribusi data.
Ukuran letak/posisi data antara lain:
median, kuartil, desil, dan persentil.
P12_Ukuran Letak (Kuartil)_M.Jainuri, M.Pd

3. KUARTIL (K)
3
Kuartil (K) adalah:
ukuran letak yang membagi suatu
distribusi data dalam empat bagian yang
sama setelah data diurutkan menurut
besarnya dari data terkecil ke data
terbesar.
P12_Ukuran Letak (Kuartil)_M.Jainuri, M.Pd

4. KUARTIL (K)
4
Perhatikan letak kuartil (K) pada garis bilangan
berikut:
P12_Ukuran Letak (Kuartil)_M.Jainuri, M.Pd
K1 : Kuartil Bawah
K2 : Median
K3 : Kuartil Atas

5. KUARTIL (K) DATA TUNGGAL
5
Tahap menghitung nilai kuartil data tunggal:
1. Terlebih dahulu cari letak/posisi kuartil yang dicari
nilainya.
2. Tentukan nilai kuartil tersebut berdasarkan
letak/posisi.
Letak kuartil dapat dicari menggunakan rumus:
P12_Ukuran Letak (Kuartil)_M.Jainuri, M.Pd

6. KUARTIL (K) DATA TUNGGAL
6
Contoh (1):
Diketahui data sebagai berikut: 8, 4, 15, 2, 18, 6, 4.
tentukan kuartil 1 (K1), kuartil 2 (K2), dan kuartil 3 (K3)!
Penyelesaian:
1. Susun data dari terkecil hingga data terbesar:
2, 4, 4, 6, 8, 15, 18.
2. Menentukan letak dan nilai kuartil:
Diketahui: i = 1, 2, atau 3
n = 7
P12_Ukuran Letak (Kuartil)_M.Jainuri, M.Pd

7. KUARTIL (K) DATA TUNGGAL
7
Penyelesaian:
P12_Ukuran Letak (Kuartil)_M.Jainuri, M.Pd

8. KUARTIL (K) DATA TUNGGAL
8
Penyelesaian:
P12_Ukuran Letak (Kuartil)_M.Jainuri, M.Pd

9. KUARTIL (K) DATA TUNGGAL
9
Penyelesaian:
P12_Ukuran Letak (Kuartil)_M.Jainuri, M.Pd

10. KUARTIL (K) DATA TUNGGAL
10
Menggunakan SPSS v25
P12_Ukuran Letak (Kuartil)_M.Jainuri, M.Pd

11. KUARTIL (K) DATA TUNGGAL
Contoh (2):
Diketahui data sebagai berikut: 8, 6, 15, 2, 18,
10, 4, 20. tentukan kuartil 1 (K1), kuartil 2 (K2),
dan kuartil 3 (K3)!
Penyelesaian:
1. Susun data dari terkecil hingga data
terbesar: 2, 4, 6, 8, 10, 15, 18, 20.
d1, d2, d3, d4, d5, d6, d7, d8
2. Menentukan letak dan nilai kuartil:
Diketahui: i = 1, 2, atau 3
n = 8
11
P12_Ukuran Letak (Kuartil)_M.Jainuri, M.Pd

12. KUARTIL (K) DATA TUNGGAL
Penyelesaian:
12
P12_Ukuran Letak (Kuartil)_M.Jainuri, M.Pd

13. KUARTIL (K) DATA TUNGGAL
Penyelesaian:
13
P12_Ukuran Letak (Kuartil)_M.Jainuri, M.Pd

14. KUARTIL (K) DATA TUNGGAL
Penyelesaian:
14
P12_Ukuran Letak (Kuartil)_M.Jainuri, M.Pd

15. KUARTIL (K) DATA TUNGGAL
Menggunakan SPPS v25
15
P12_Ukuran Letak (Kuartil)_M.Jainuri, M.Pd

16. Letak/posisi dan nilai kuartil data kelompok dapat
dicari menggunakan rumus berikut:
16
P12_Ukuran Letak (Kuartil)_M. Jainuri, S.Pd., M.Pd

17. Contoh:
Diketahui nilai mata kuliah “Listening I” mahasiswa
Pendidikan Bahasa Inggris sebagi berikut:
Tentukan K1, K2, K3 dari data di atas!
17
P12_Ukuran Letak (Kuartil)_M. Jainuri, S.Pd., M.Pd

18. Penyelesaian:
1. Membuat tabel bantu:
18
P12_Ukuran Letak (Kuartil)_M. Jainuri, S.Pd., M.Pd

19. Penyelesaian:
2. Menentukan letak/posisi kuartil:
Pada kolom frekuensi komulatif kurang dari (fk <)
pada tabel Langkah 1 di atas, 12,5 terdapat pada
kelas kedua.
19
P12_Ukuran Letak (Kuartil)_M. Jainuri, S.Pd., M.Pd
i 1
i 1
K = (n) K = (50) = 12,5
4 4
→

20. Penyelesaian:
Pada kolom frekuensi komulatif kurang dari (fk <) pada
tabel Langkah 1 di atas, 25 terdapat pada kelas ketiga.
Pada kolom frekuensi komulatif kurang dari (fk <) pada
tabel Langkah 1 di atas, 37,5 terdapat pada kelas
keempat.
20
P12_Ukuran Letak (Kuartil)_M. Jainuri, S.Pd., M.Pd
i 2
i 2
K = (n) K = (50) = 25
4 4
→
i 3
i 3
K = (n) K = (50) = 37,5
4 4
→

21. Penyelesaian:
3. Mengitung nilai kuartil:
21
P12_Ukuran Letak (Kuartil)_M. Jainuri, S.Pd., M.Pd
R 14
I = 2,8 3
K 5
= = 

22. Penyelesaian:
22
P12_Ukuran Letak (Kuartil)_M. Jainuri, S.Pd., M.Pd

23. Penyelesaian:
23
P12_Ukuran Letak (Kuartil)_M. Jainuri, S.Pd., M.Pd

24. JANGKAUAN INTERKUARTIL (KR)
24
Jangkauan interkuartil adalah selisih antara kuartil atas (K3)
dan kuartil bawah (K1). Jika jangkauan interkuatil dinotasikan
dengan KR, maka KR dapat dihitung dengan rumus berikut:
KR = K3 – K1
Keterangan :
KR = Jangkauan Interkuartil
K1 = Kuartil bawah atau kuartil ke-1
K3 = Kuartil atas atau kuartil ke-3

25. SIMPANGAN KUARTIL (Kd)
25
Simpangan kuartil (jangkauan semi interkuartil)
adalah setengah dari jangkauan interkuartil. Jika jangkauan
semi interkuartil dinotasikan dengan Kd, maka Kd dapat
dihitung dengan rumus:
Kd = ½ (K3 – K1)
Keterangan :
Kd = Simpangan kuartil
K1 = Kuartil bawah atau kuartil ke-1
K3 = Kuartil atas atau kuartil ke-3
P12_Ukuran Letak (Kuartil)_M.Jainuri, M.Pd

26. CONTOH:
26
Perhatikan kembali Contoh (1) data tunggal (Slide 6),
dari hasil perhitungan contoh (1) tersebut diketahui K1 =
4 dan K3 = 15.Tentukan jangkauan interkuartil dan
simpangan kuartilnya!
Penyelesaian:
Jangkauan Interkuartil:
KR = K3 – K1
= 15 – 4
= 11
Simpangan kuartil:
Kd = ½ (K3 – K1)
= ½ (15 – 4)
= ½ (11)
= 5,5

27. LATIHAN
Diketahui distribusi nilai dari 36 siswa sebagai
berikut:
Jika rata-ratanya adalah 60, tentukan nilai K1,
K2,K3, dan simpangan kuartil (Kd) dari data
tersebut!
P12_Ukuran Letak (Kuartil)_M. Jainuri, S.Pd., M.Pd 27
Nilai 30 40 50 60 70 80 90
F 3 4 x 7 y 5 4

28. Penyelesaian
Langkah 1:
Cari terlebih dahulu berapa jumlah siswa yang
memperoleh nilai 50 yaitu (x), dan jumlah siswa
yang memperoleh nilai 60 yaitu (y) dari 36 orang
siswa. Caranya, buat persamaan matematika
dari data pada contoh, yaitu:
❖ Baris F (frekuensi):
3 + 4 + x + 7 + y + 5 + 4 = 36
x + y + 23 = 36
x + y = 36 – 23
x + y = 13 Persamaan (1)
P12_Ukuran Letak (Kuartil)_M. Jainuri, S.Pd., M.Pd 28

29. Penyelesaian
❖ Baris Nilai
Diketahui jumlah siswa adalah 36 dan rata-rata ( ҧ
𝑥)
adalah 60, sehingga:
P12_Ukuran Letak (Kuartil)_M. Jainuri, S.Pd., M.Pd 29
30.3 40.4 50. 60.7 70.y 80.5 90.4
36
x
x
+ + + + + +
=
90 160 50 420 70 y 400 360
60
36
x
+ + + + + +
=
1430 50 70 y
60
36
x
+ +
=
60.36 1430 50 70 y
x
= + +
2160 1430 50 70 y
x
= + +

30. Penyelesaian
Persamaan (2)
Langkah 2:
❖ubah bentuk persamaan (1):
x + y = 13
❖menjadi:
x = 13 – y
P12_Ukuran Letak (Kuartil)_M. Jainuri, S.Pd., M.Pd 30
1430 50 70 y 2160
x
+ + =
50 70 y 2160 1430
x + = −
50 70 y 730
x + =

31. Penyelesaian
❖Substitusikan persamaan (1) ke persamaan (2),
sehingga diperoleh nilai (x) dan (y) sebagai
berikut:
50x + 70y = 730
50(13-y) + 70y = 730
50.13 – 50.y + 70y = 730
650 – 50y + 70y = 730
650 + 20y = 730
20y = 730 – 650
20y = 80
y = 80 : 20 = 4
P12_Ukuran Letak (Kuartil)_M. Jainuri, S.Pd., M.Pd 31
Diketahui nilai y = 4,
masukan ke dalam
persamaan x, maka:
x = 13 – y
x = 13 – 4
x = 9

32. Penyelesaian
❖Melengkapi tabel dengan memasukkan nilai (x)
dan (y), dan menambahkan kolom Fk <
sehingga:
P12_Ukuran Letak (Kuartil)_M. Jainuri, S.Pd., M.Pd 32
Nilai 30 40 50 60 70 80 90
F 3 4 4 7 9 5 4
Fk < 3 7 11 18 27 32 36

33. Penyelesaian
Langkah 3:
Menentukan nilai K1, K2, K3, dan simpangan
kuartil (Kd)
Letak kuartil 1 (K1): Nilai kuartil 1 (K1):
P12_Ukuran Letak (Kuartil)_M. Jainuri, S.Pd., M.Pd 33
i
i
K = (n+1)
4
1
i
K = (36+1)
4
1
1 2
K = (37) = 9
4 4
Nilai K1 = nilai d9 + 2/4 (d10 - d9)
= 50 + 2/4 (50 – 50)
= 50 + 0
= 50
Jadi, nilai K1 = 50

34. Penyelesaian
Letak kuartil 2 (K2):
Nilai kuartil 2 (K2):
P12_Ukuran Letak (Kuartil)_M. Jainuri, S.Pd., M.Pd 34
i
i
K = (n+1)
4
2
2
K = (36+1)
4
1
1 1
K = (37) = 18
2 2
Nilai K2 = nilai d18 + ½ (d19 - d18)
= 60 + ½ (70 – 60)
= 60 + ½(10)
= 60 + 5
= 65
Jadi, nilai K2 = 65

35. Penyelesaian
Letak kuartil 3 (K3):
Nilai kuartil 3 (K3):
P12_Ukuran Letak (Kuartil)_M. Jainuri, S.Pd., M.Pd 35
i
i
K = (n+1)
4
3
3
K = (36+1)
4
3
3 3
K = (37) = 27
4 4
Nilai K3 = nilai d27 + 3/4 (d28 - d27)
= 70 + 3/4 (80 – 70)
= 70 + 3/4(10)
= 70 + 7,5
= 77,5
Jadi, nilai K3 = 77,5

36. Penyelesaian
Simpangan Kuartil (Kd):
P12_Ukuran Letak (Kuartil)_M. Jainuri, S.Pd., M.Pd 36
Kd = ½ (K3 – K1)
= ½ (77,5 – 50)
= ½ (27,5)
= 27,5
Jadi, nilai Kd = 27,5