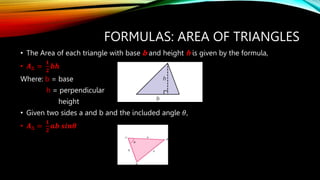
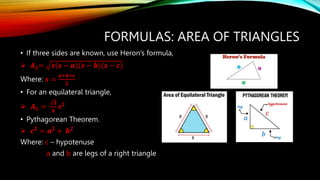
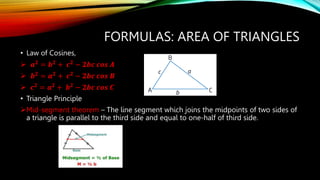
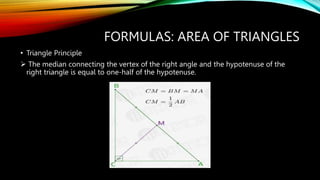
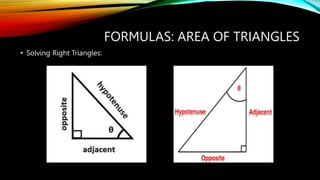
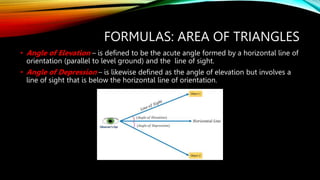
This document provides formulas and concepts related to polygons and triangles. It defines perimeter and area for regular polygons. Formulas are given for the number of sides, diagonals, triangles formed by diagonals, and interior/central angles of regular polygons. Triangles are classified based on sides and angles. Formulas are presented for finding the area of triangles given base/height, two sides and included angle, three sides using Heron's formula, and for right triangles using Pythagorean theorem and trigonometric functions. Laws of cosines and triangle principles like mid-segment theorem are also summarized.

1. INSTRUCTOR: ENGR. MA. JESSA P. DOLLADO, MP

2. FORMULAS IN POLYGONS
PERIMETER – is the length around the
boundary of a closed two-dimensional region.
AREA – is the amount of material that would
be needed to cover a surface completely.
• Perimeter of regular polygon,
𝑷 = 𝒔𝒏
Where: n = number of sides
s = measure of one side
• Area of regular polygon,
A=
𝟏
𝟐
Pa or A=
𝒔𝟐𝒏
𝟒𝐭𝐚𝐧(
𝟏𝟖𝟎°
𝒏
)
Where: P = perimeter
a = apothem
s = measure of one side
n = number of sides
• Apothem of a regular polygon,
a=
𝒔
𝟐𝐭𝐚𝐧(
𝟏𝟖𝟎°
𝒏
)
s = measure of one side
n = number of sides

3. FORMULAS IN POLYGONS
• Number of diagonals in a polygon,
d=
𝒏
𝟐
(𝒏 − 𝟑)
Where: n = number of sides
• Number of triangles formed by
Diagonals drawn through the same vertex,
t = 𝒏 − 𝟐
Where: n = number of sides
• Central Angle in a regular polygon,
𝜽𝒄=
𝟑𝟔𝟎°
𝐧
Where: n = number of sides
• Each interior angle of a regular polygon,
𝜽𝑰=(
𝒏−𝟐
𝒏
) 180°
Where: n = number of sides

4. FORMULAS IN POLYGONS
• Sum of interior Angles,
𝑰𝒔 = 𝒏 − 𝟐 𝟏𝟖𝟎°
Where: n = number of sides

5. TRIANGLES
• TRIANGLE – a triangle is a type of polygon, which has three sides, and the two sides
are joined end to end is called the vertex. An angle is formed between two sides.
The sum of all three interior angles is equal to 180 degrees.
• If ABC is a triangle, then it is denoted as ∆ABC, where A, B and C are the vertices of
the triangle.
• If we extend the side length outwards, then it forms an exterior angle. The sum of
consecutive interior and exterior angles of a triangle is supplementary.

6. CLASSIFICATION OF TRIANGLES
• ACCORDING TO SIDES
A. Equilateral Triangle – is a three-sided polygon with three equal sides and interior
angles.
B. Isosceles Triangle – is a three-sided polygon with two equal sides.
C. Scalene Triangle – is a three-sided polygon with no equal sides.
• ACCORDING TO ANGLES
A. Right Triangle – is a three-sided polygon with one right angle.
B. Oblique Triangle – is a triangle with no right angle.
1. Equiangular triangle – is a triangle having three equal angles.
2. Acute triangle – is a triangle having three acute angles.
3. Obtuse triangle – is a triangle having one obtuse angle.

7. CLASSIFICATION OF TRIANGLES

8. FORMULAS: AREA OF TRIANGLES
• The Area of each triangle with base b and height h is given by the formula,
• 𝑨∆ =
𝟏
𝟐
𝒃𝒉
Where: b = base
h = perpendicular
height
• Given two sides a and b and the included angle 𝜃,
• 𝑨∆ =
𝟏
𝟐
𝒂𝒃 𝒔𝒊𝒏𝜽

9. FORMULAS: AREA OF TRIANGLES
• If three sides are known, use Heron’s formula,
 𝑨∆= 𝒔(𝒔 − 𝒂)(𝒔 − 𝒃)(𝒔 − 𝒄)
Where: 𝒔 =
𝒂+𝒃+𝒄
𝟐
• For an equilateral triangle,
 𝑨∆ =
𝟑
𝟒
𝒔𝟐
• Pythagorean Theorem.
 𝒄𝟐 = 𝒂𝟐 + 𝒃𝟐
Where: c – hypotenuse
a and b are legs of a right triangle

10. FORMULAS: AREA OF TRIANGLES
• Law of Cosines,
 𝒂𝟐
= 𝒃𝟐
+ 𝒄𝟐
− 𝟐𝒃𝒄 𝒄𝒐𝒔 𝑨
 𝒃𝟐
= 𝒂𝟐
+ 𝒄𝟐
− 𝟐𝒃𝒄 𝒄𝒐𝒔 𝑩
 𝒄𝟐
= 𝒂𝟐
+ 𝒃𝟐
− 𝟐𝒃𝒄 𝒄𝒐𝒔 𝑪
• Triangle Principle
Mid-segment theorem – The line segment which joins the midpoints of two sides of
a triangle is parallel to the third side and equal to one-half of third side.

11. FORMULAS: AREA OF TRIANGLES
• Triangle Principle
 The median connecting the vertex of the right angle and the hypotenuse of the
right triangle is equal to one-half of the hypotenuse.

12. FORMULAS: AREA OF TRIANGLES
• Triangle Principle
 Right Triangle Principle – If ∆𝑄𝑅𝑆 is a right triangle and RT ⊥ QS, then ∆𝑄𝑅𝑆,and
∆𝑅𝑇𝑆 are similar.

13. FORMULAS: AREA OF TRIANGLES
• Solving Right Triangles:

14. FORMULAS: AREA OF TRIANGLES
• Trigonometric Functions of an acute angle of a triangle.

15. FORMULAS: AREA OF TRIANGLES
• Angle of Elevation – is defined to be the acute angle formed by a horizontal line of
orientation (parallel to level ground) and the line of sight.
• Angle of Depression – is likewise defined as the angle of elevation but involves a
line of sight that is below the horizontal line of orientation.