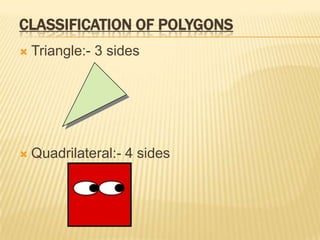
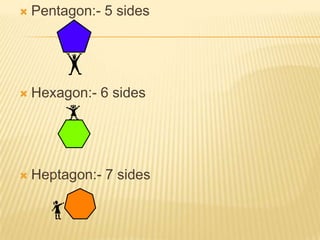
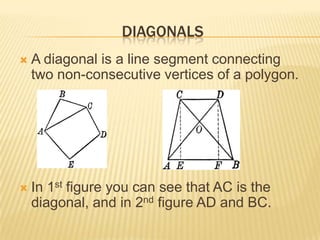
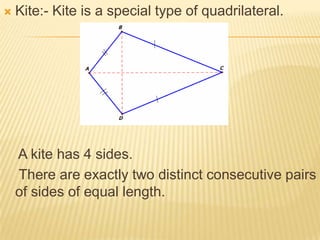
The document provides an overview of polygons, defining them as closed curves made of line segments and categorizing them based on the number of sides such as triangles, quadrilaterals, and more. It also discusses properties of various quadrilaterals like trapeziums, kites, parallelograms, rhombuses, rectangles, and squares, highlighting their characteristics and relationships. Additionally, it notes the angle sum properties of polygons and the significance of diagonals.