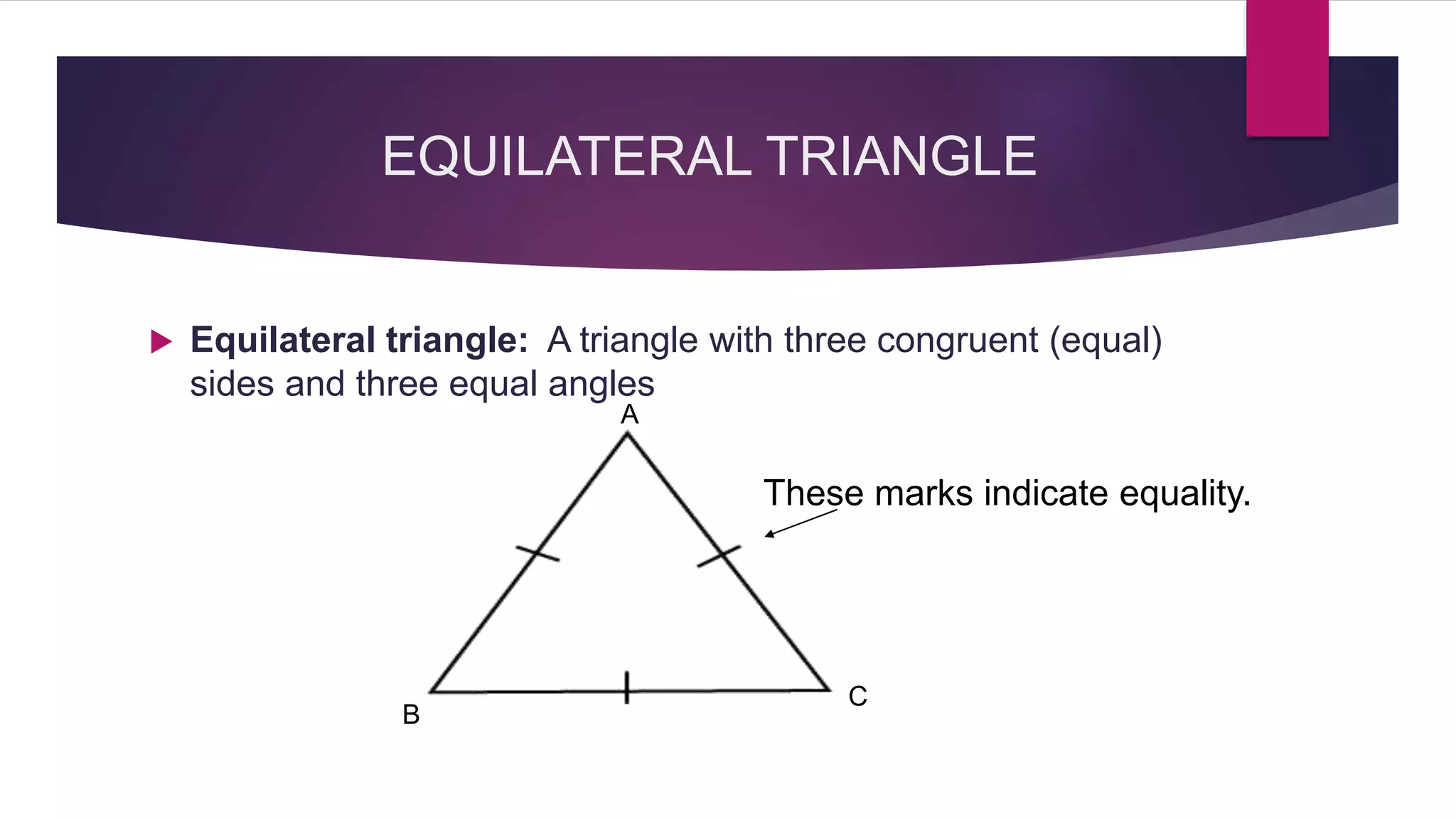
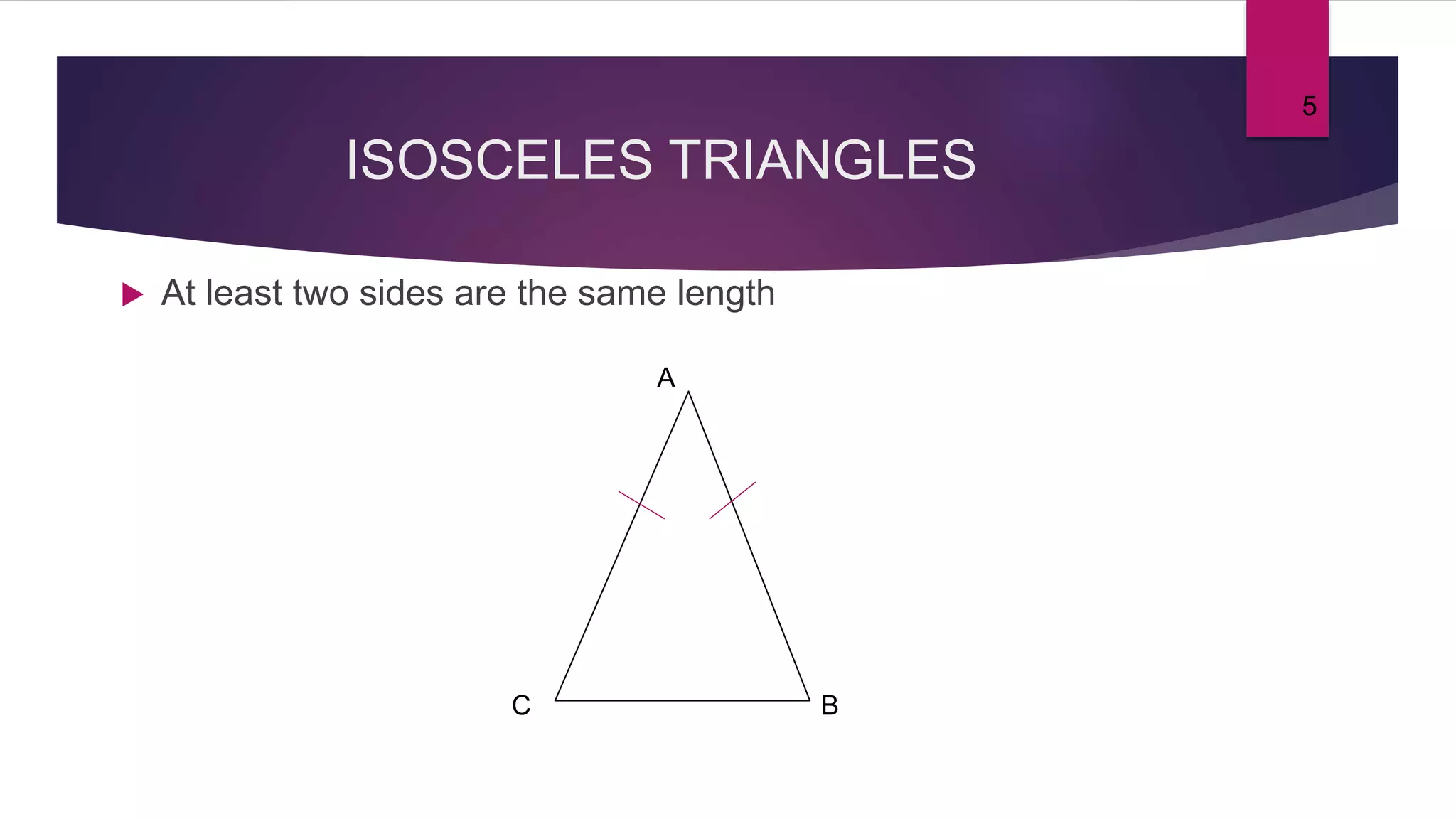
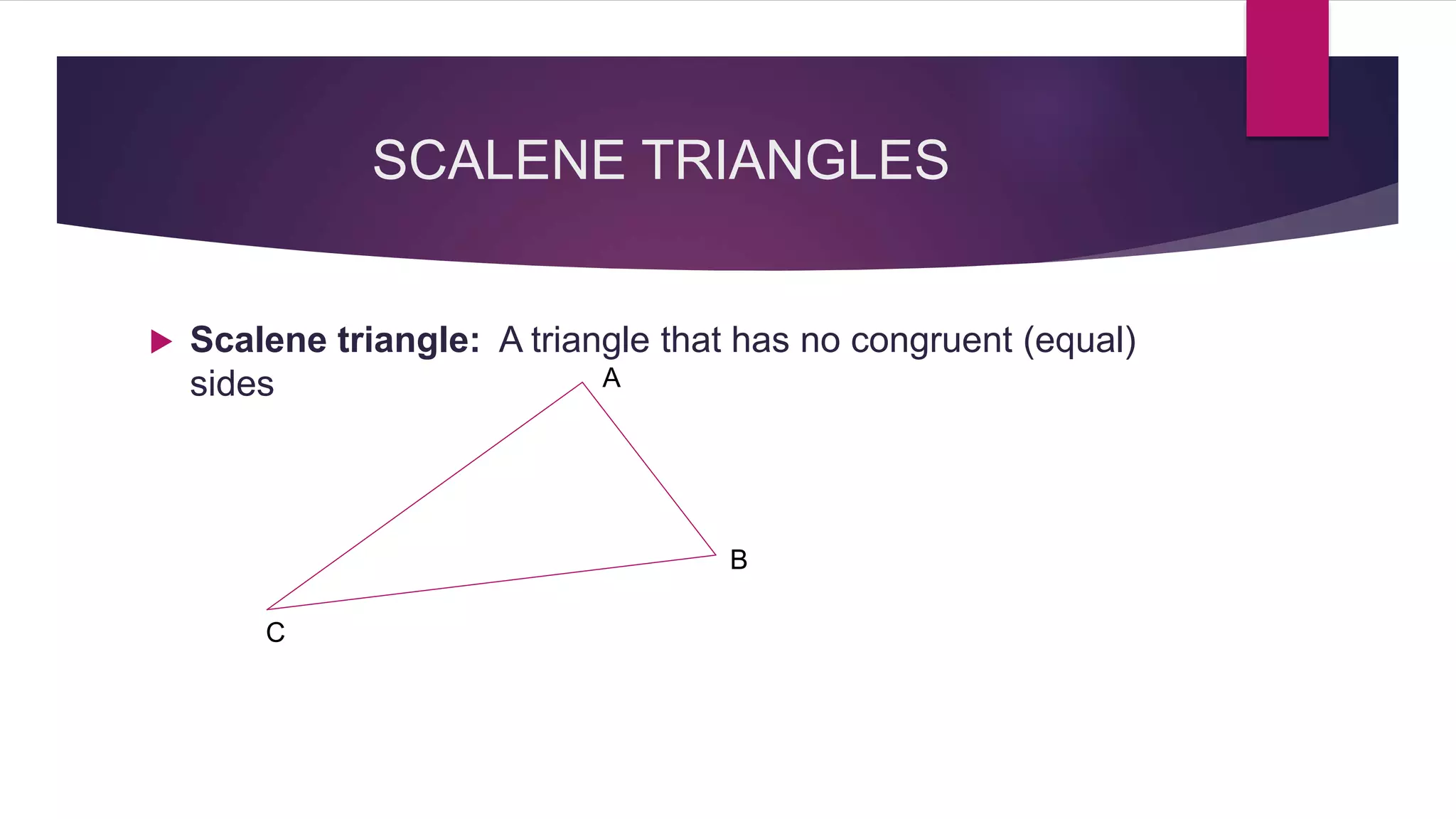
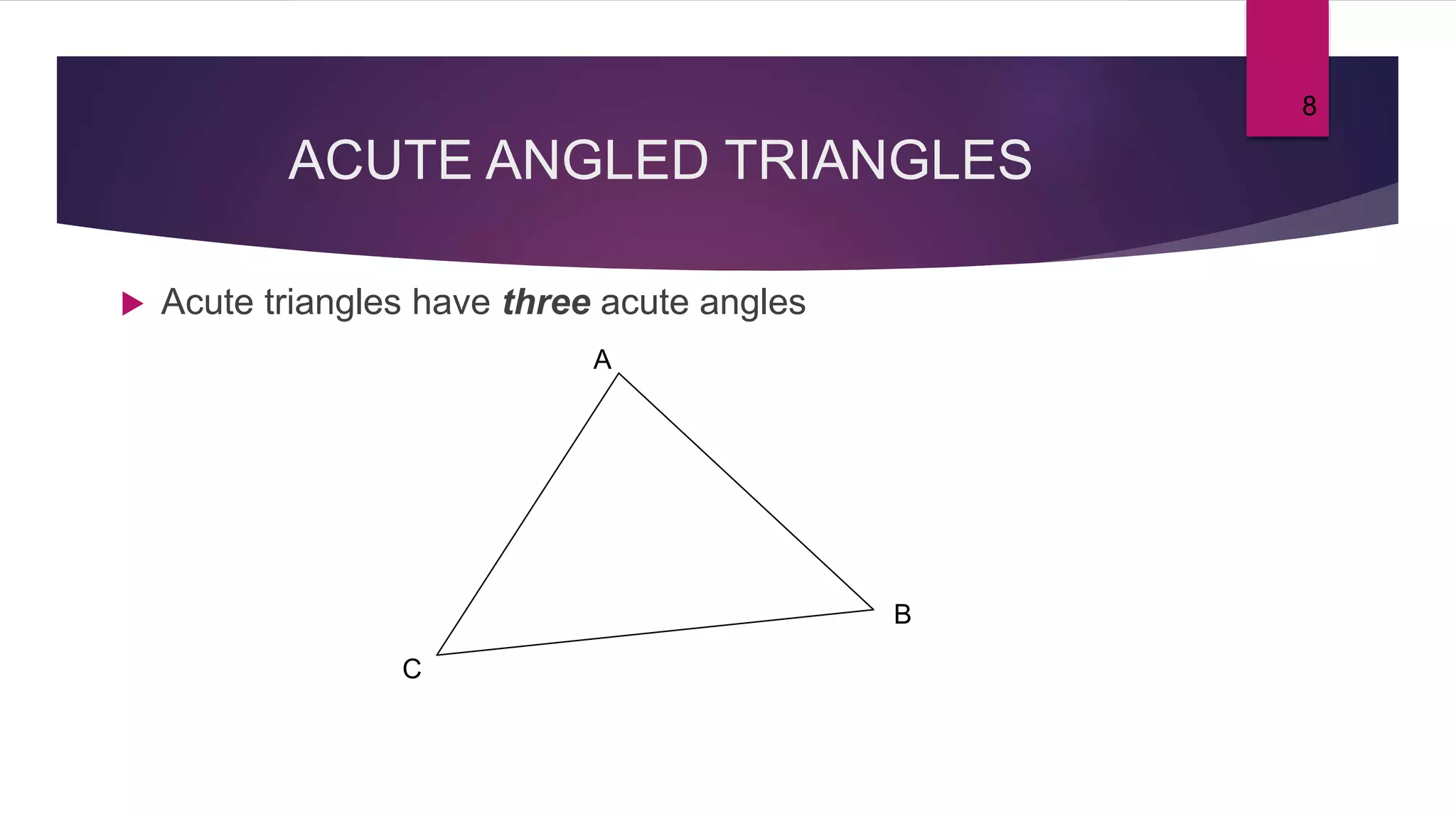
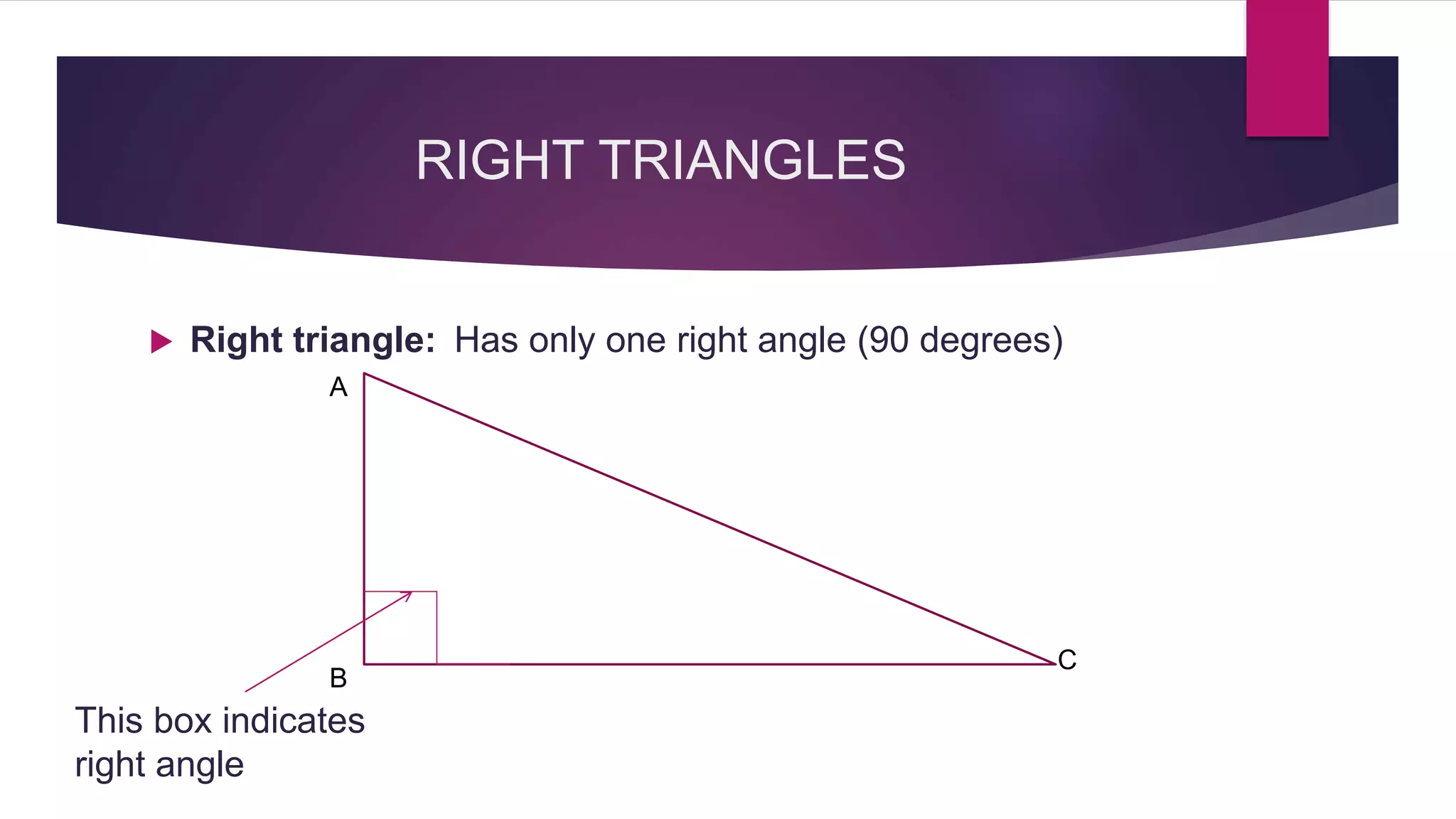
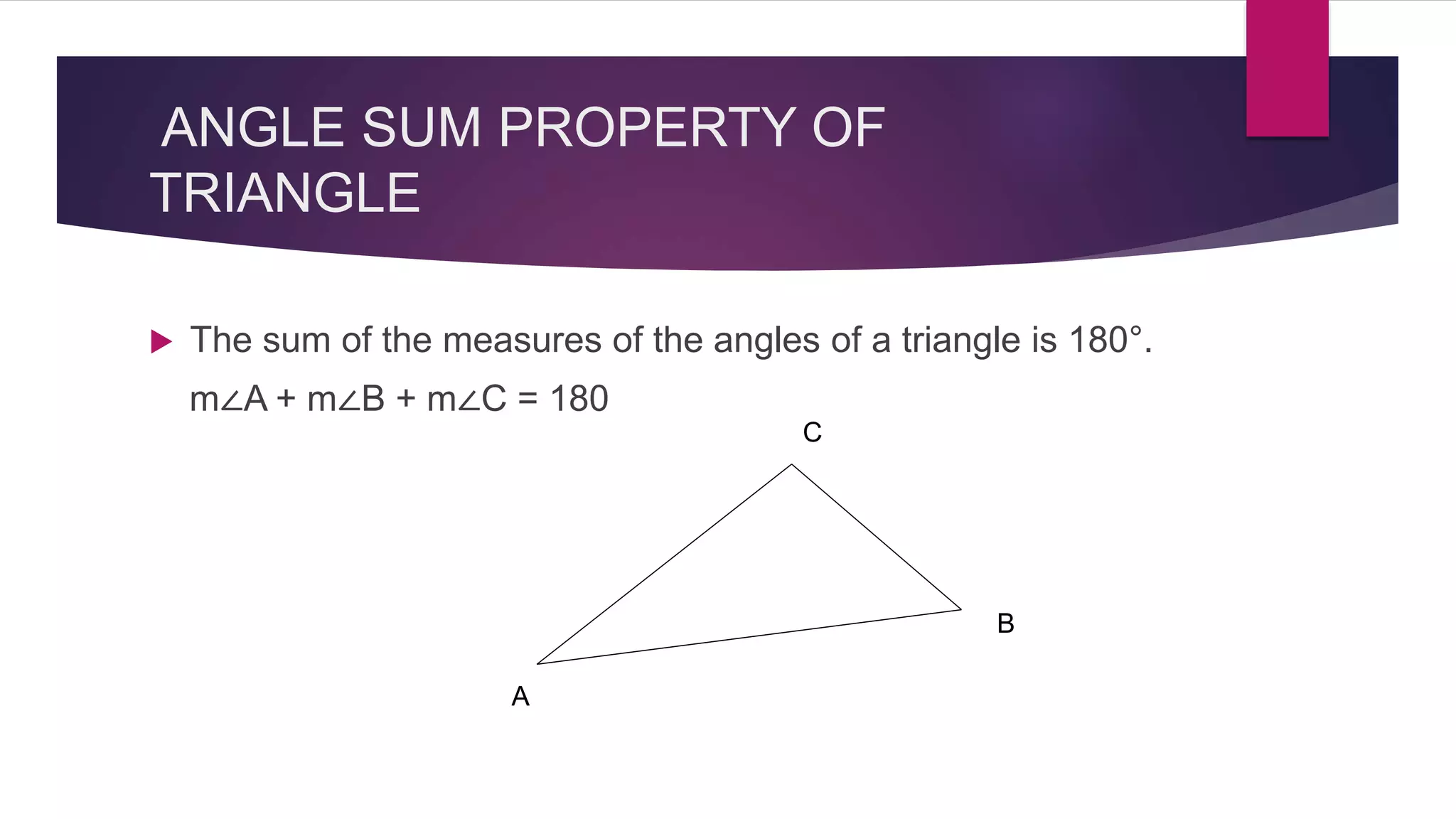
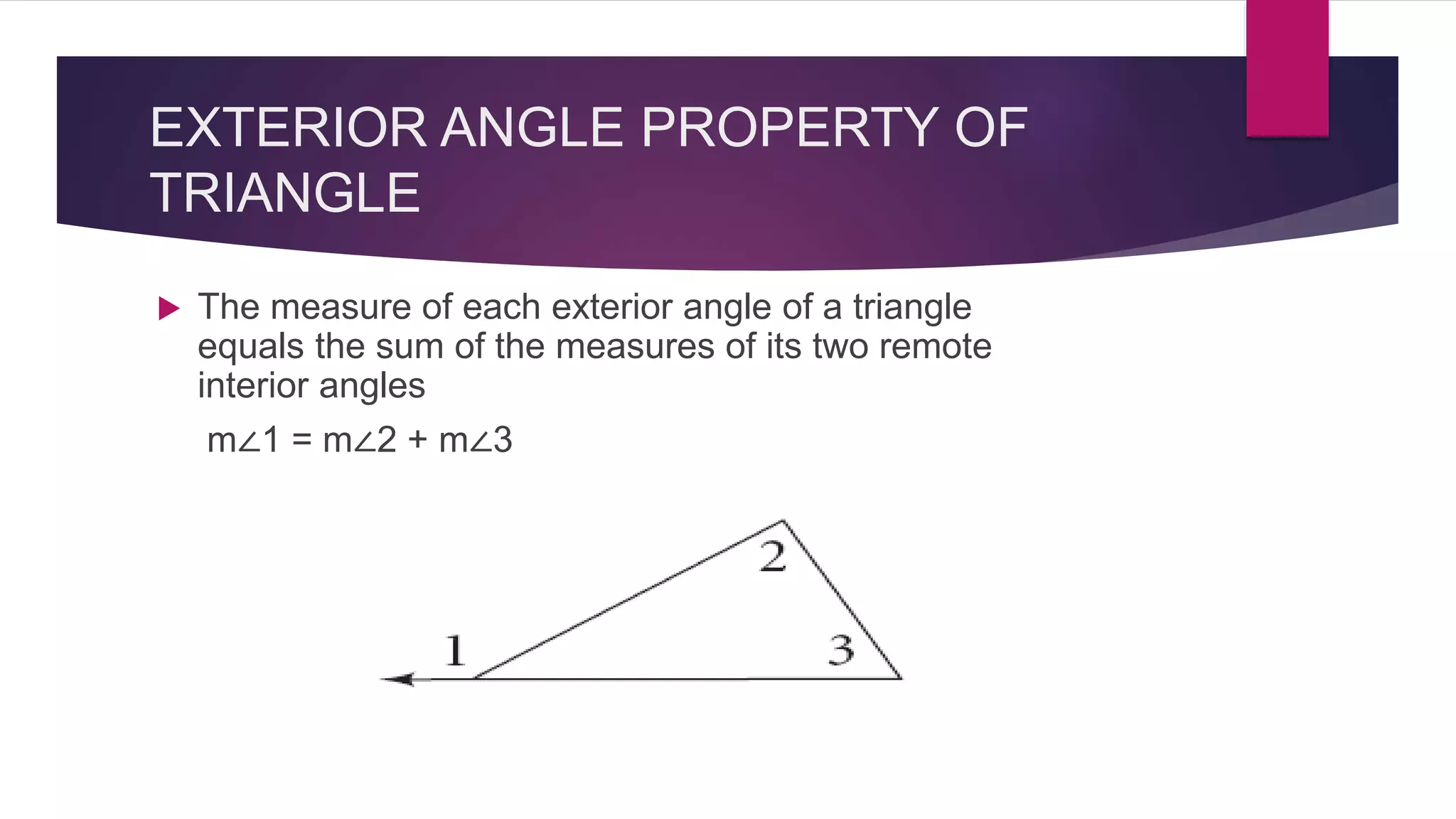
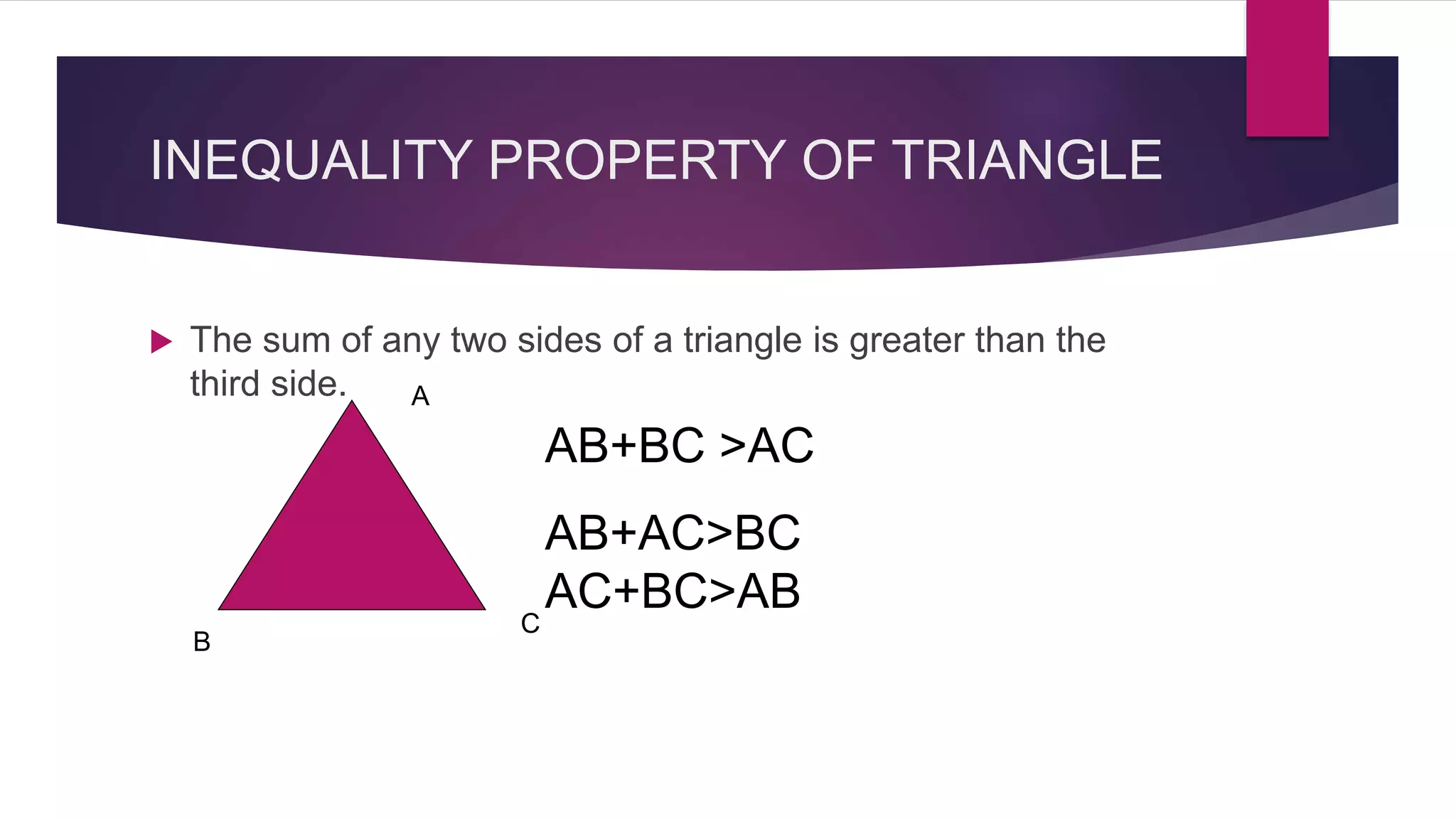
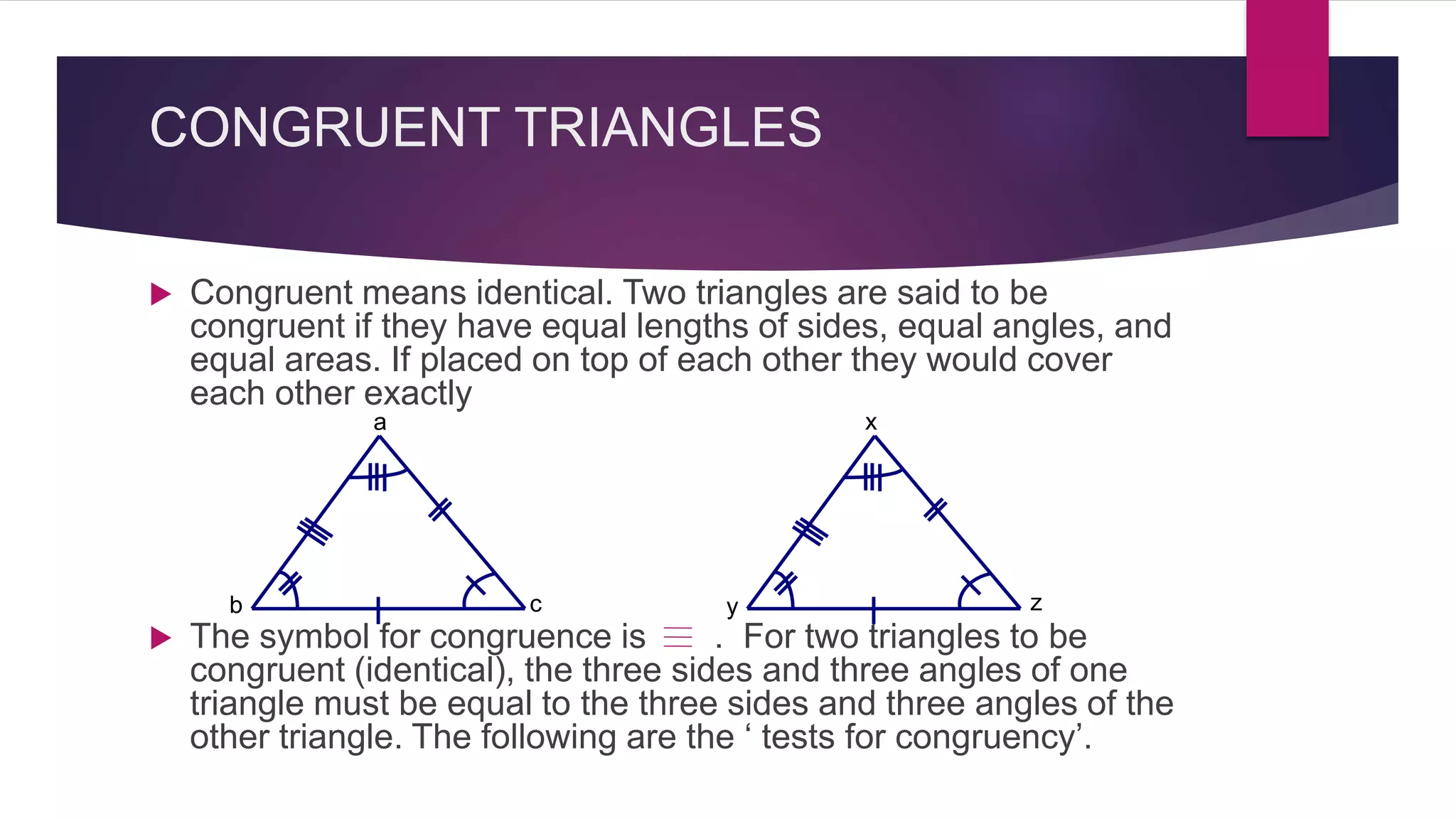
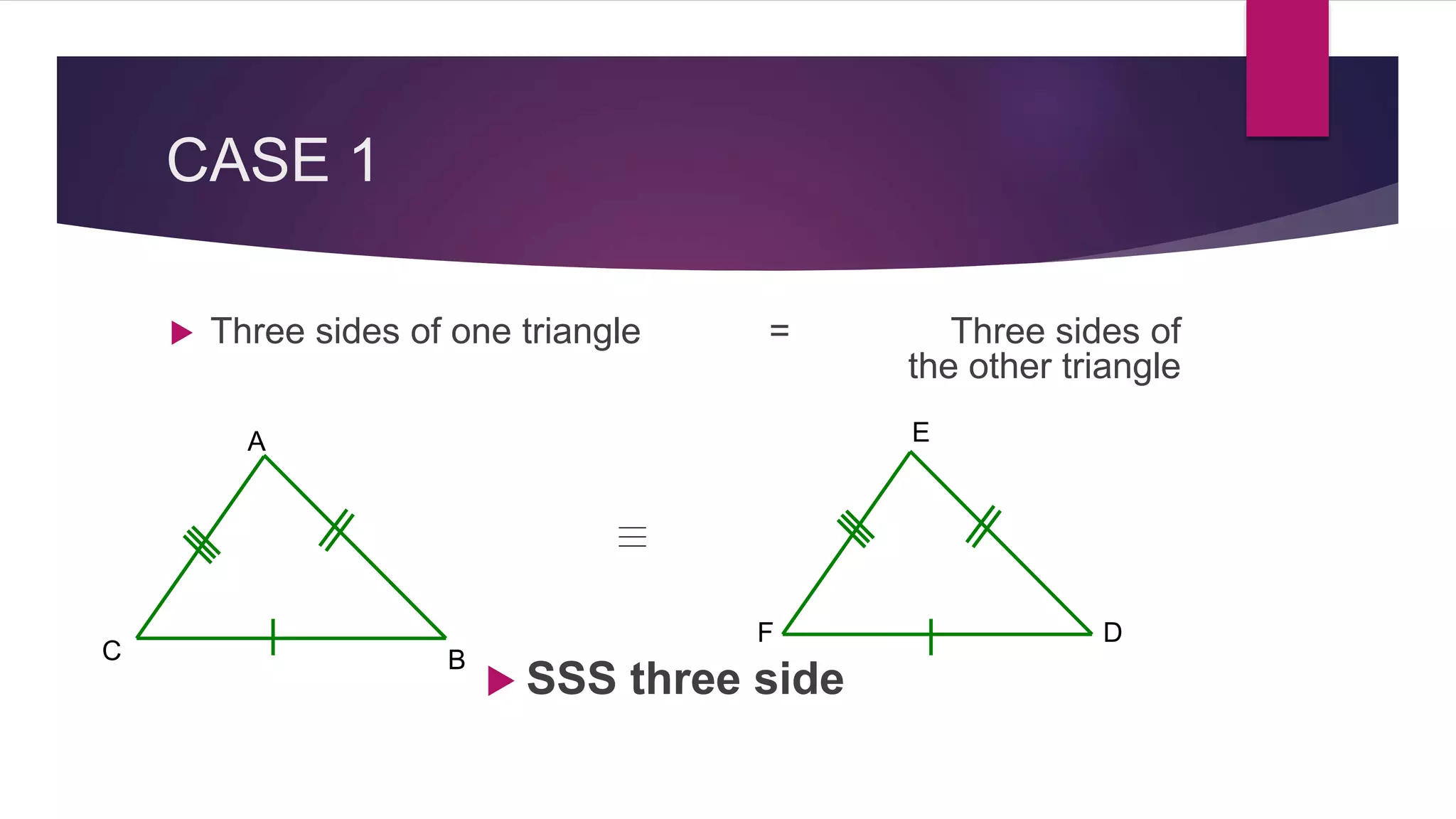
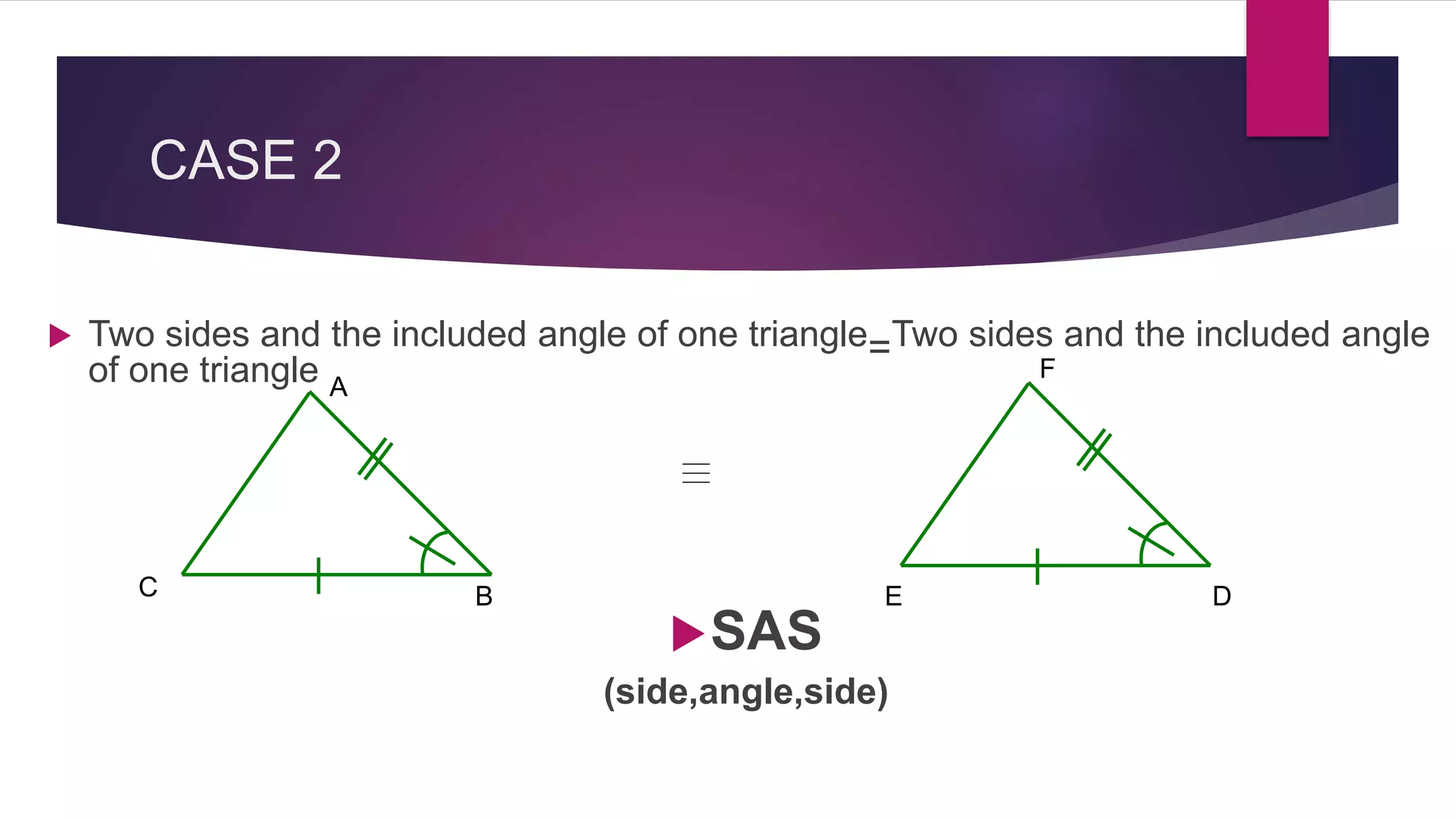
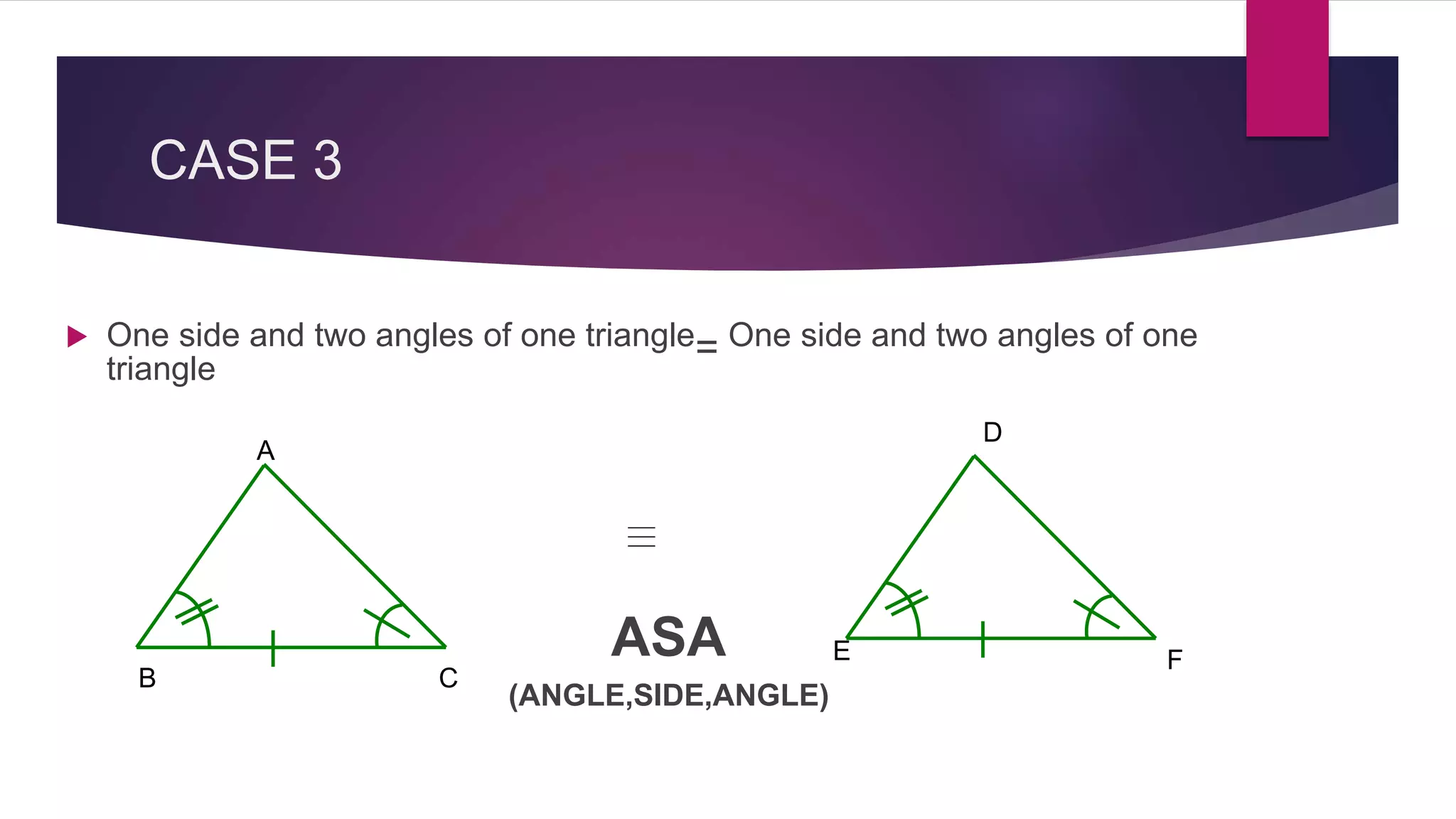
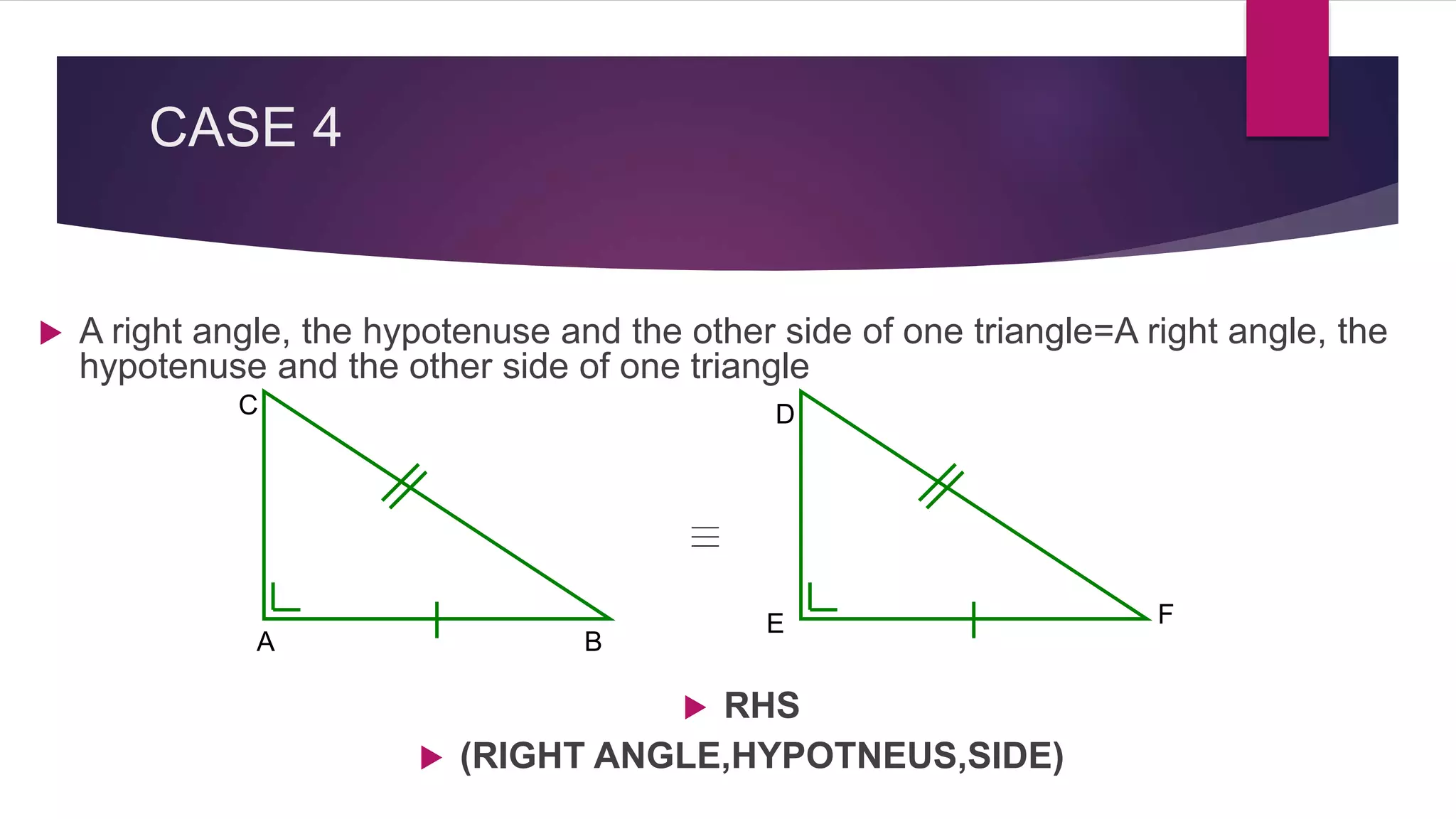
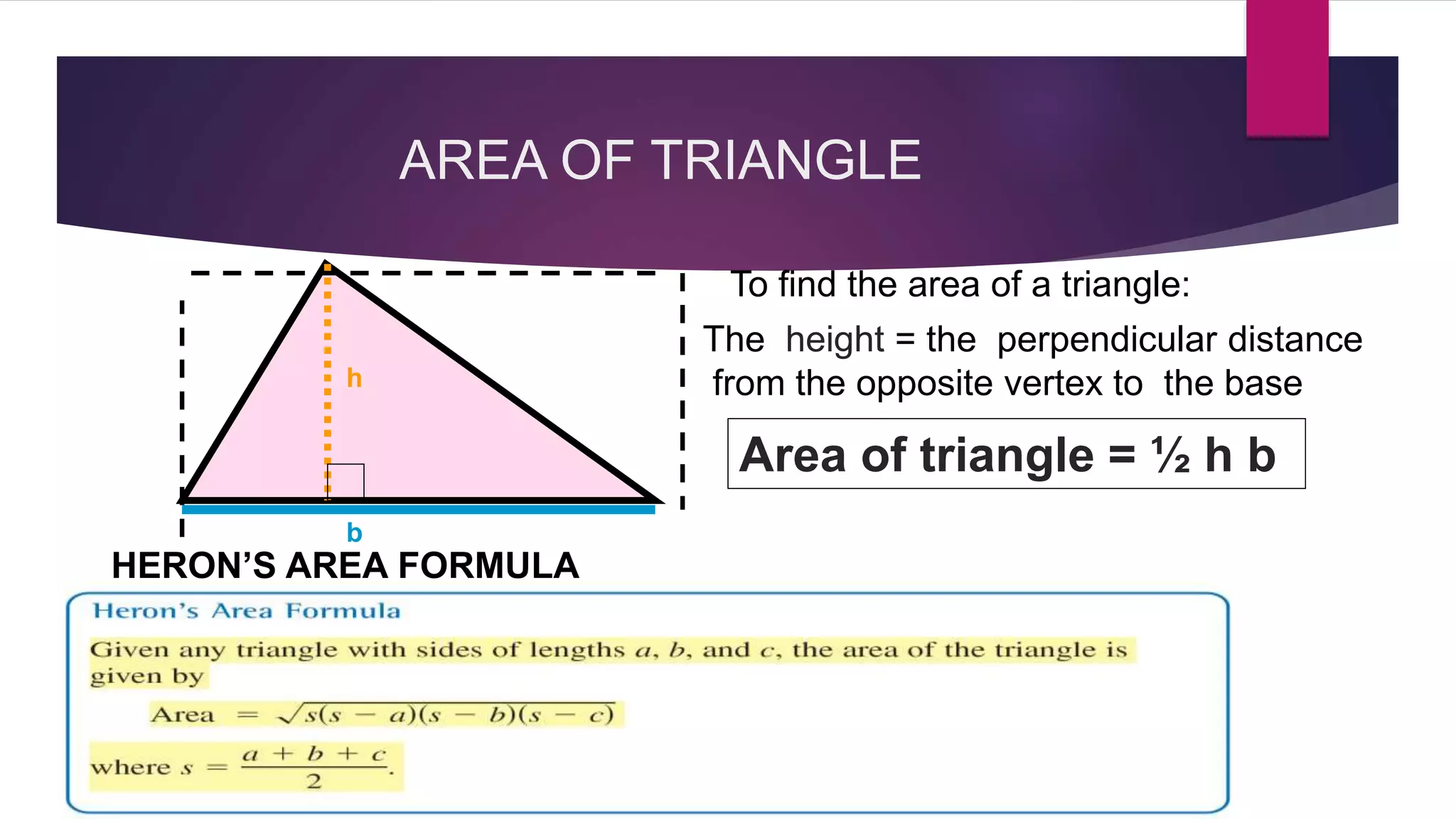
The document provides an overview of triangles, detailing their definition, types based on sides and angles, and key properties such as the angle sum property and the Pythagorean theorem. It also explains congruence in triangles, outlining tests for congruency, and presents formulas for calculating the area of triangles. Overall, the document serves as a foundational guide to understanding the properties and classifications of triangles.

1. PREPARED BY:
MINHAJ NOUSHAD ,
TRIANGLES
AND ITS
PROPERTIES

2. INTRODUCTION
Polygon
Polygon is a simple close curve formed by the line segments is
called a polygon. Triangle s a polygon with least number of
lines
Triangle
 A plane figure formed by three non parallel line segment
is called a triangle
Elements of triangle
 The three sides AB,BC,AC and angle abc,, angle bac and angle
acb denoted by angle a, angle b and angle c together is known as
six part of or elements of triangle abc
a
bc

3. TYPES OF TRIANGLES
(BASED ON ITS SIDES)

4. EQUILATERAL TRIANGLE
 Equilateral triangle: A triangle with three congruent (equal)
sides and three equal angles
These marks indicate equality.
A
B
C

5. ISOSCELES TRIANGLES
 At least two sides are the same length
5
A
BC

6. SCALENE TRIANGLES
 Scalene triangle: A triangle that has no congruent (equal)
sides A
B
C

7. TYPES OF TRIANGLES
(BASED ON ITS ANGLES)

8. ACUTE ANGLED TRIANGLES
 Acute triangles have three acute angles
8
A
B
C

9. RIGHT TRIANGLES
 Right triangle: Has only one right angle (90 degrees)
This box indicates
right angle
A
B
C

10. OBTUSE ANGLED TRIANGLES
 Obtuse triangles have one obtuse angle
A
B
C

11. PROPERTIES
OF
TRIANGLE

12. ANGLE SUM PROPERTY OF
TRIANGLE
 The sum of the measures of the angles of a triangle is 180°.
m∠A + m∠B + m∠C = 180
A
B
C

13. EXTERIOR ANGLE PROPERTY OF
TRIANGLE
 The measure of each exterior angle of a triangle
equals the sum of the measures of its two remote
interior angles
m∠1 = m∠2 + m∠3

14. INEQUALITY PROPERTY OF TRIANGLE
 The sum of any two sides of a triangle is greater than the
third side. A
B
C
AB+BC >AC
AB+AC>BC
AC+BC>AB

15. PYTHAGORAS THEOREM OF
TRIANGLE
 In a right triangle, the square of the longest side is equal to
the sum of squares of remaining two sides.
A
B
C
( AC)
2
= (AB)
2
+ (BC)
2
Hypotenuse
2
= Perpendicular
2
+ Base
2
Base
Perpendicular Hypotenuse

16. CONGRUENCE
OF
TRIANGLES

17. CONGRUENT TRIANGLES
 Congruent means identical. Two triangles are said to be
congruent if they have equal lengths of sides, equal angles, and
equal areas. If placed on top of each other they would cover
each other exactly
 The symbol for congruence is . For two triangles to be
congruent (identical), the three sides and three angles of one
triangle must be equal to the three sides and three angles of the
other triangle. The following are the ‘ tests for congruency’.
a
b c
x
y z

18. CASE 1
 Three sides of one triangle = Three sides of
the other triangle
 SSS three side
A E
B
F
C
D

19. CASE 2
 Two sides and the included angle of one triangle=Two sides and the included angle
of one triangle
SAS
(side,angle,side)
A
BC DE
F

20. CASE 3
 One side and two angles of one triangle= One side and two angles of one
triangle
ASA
(ANGLE,SIDE,ANGLE)
A
B C
D
E F

21. CASE 4
 A right angle, the hypotenuse and the other side of one triangle=A right angle, the
hypotenuse and the other side of one triangle
 RHS
 (RIGHT ANGLE,HYPOTNEUS,SIDE)
A B
C D
E F

22. AREA
OF A
TRIANGLE

23. To find the area of a triangle:
The height = the perpendicular distance
from the opposite vertex to the baseh
b
Area of triangle = ½ h b
AREA OF TRIANGLE
HERON’S AREA FORMULA

24. THANK YOU ALL