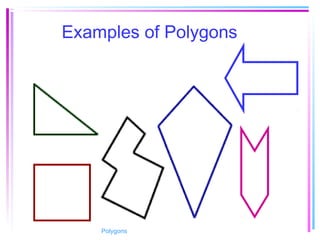
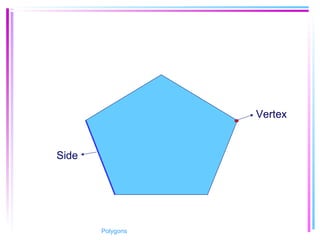
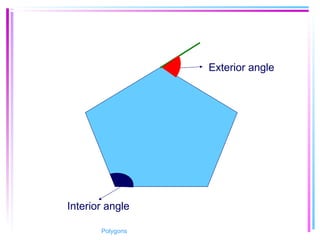
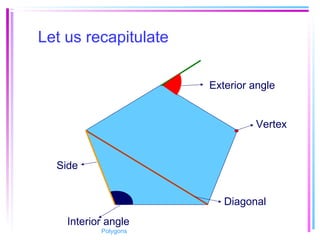
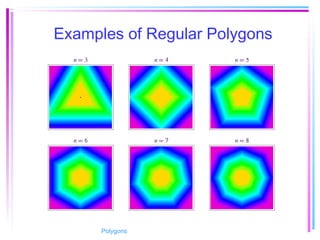
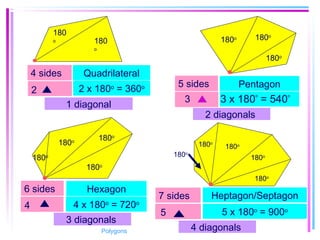
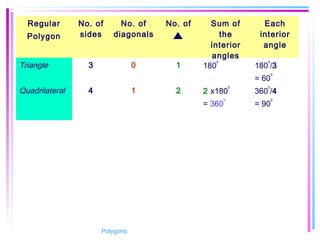
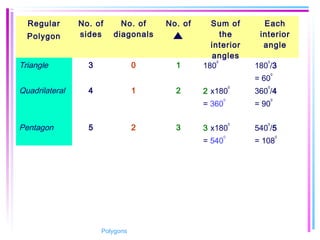
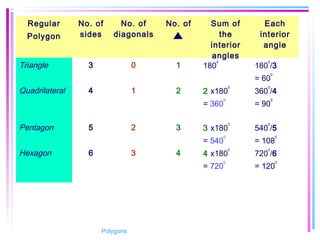
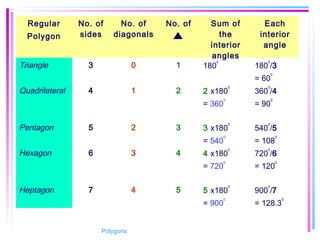
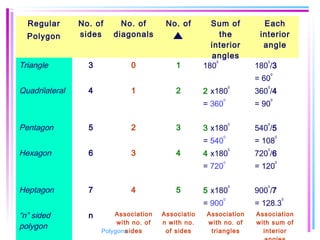
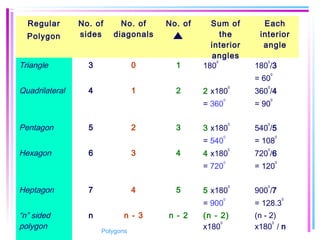
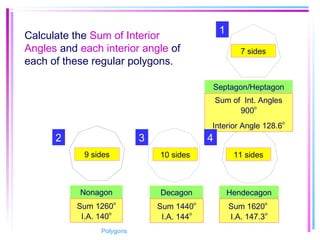
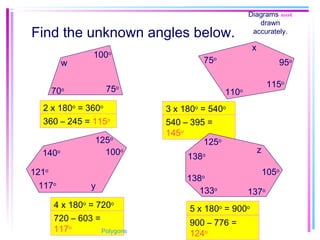
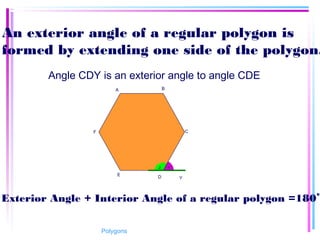
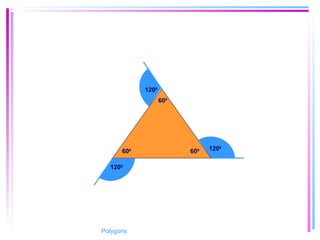
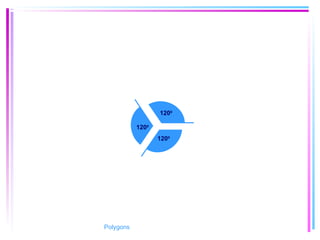
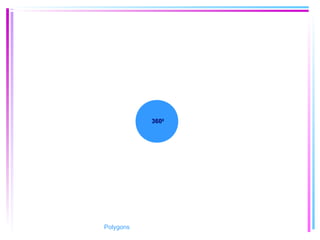
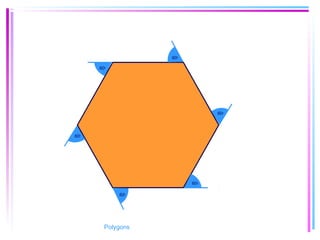
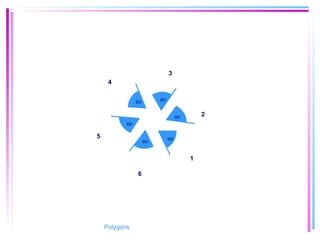
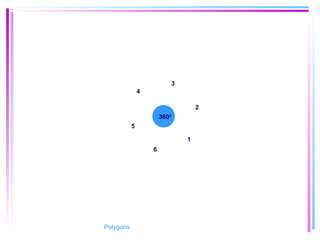
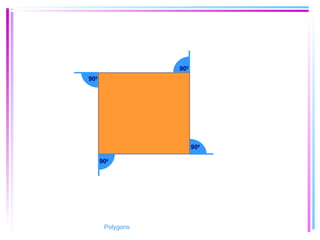
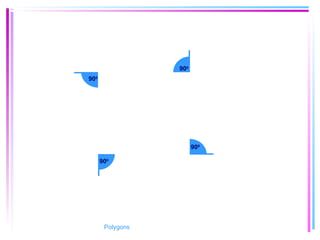
This document provides information about polygons, including definitions, terminology, properties of different types of polygons, and formulas relating the number of sides, angles, and diagonals. It defines a polygon as a closed, two-dimensional figure formed by three or more line segments. Regular polygons are introduced as those with all sides the same length and all interior angles the same measure. Formulas are given relating the number of sides of a regular polygon to the sum of its interior angles, the measure of each interior angle, and the number of diagonals and triangles it contains. Interior and exterior angles are defined and their relationships explored. Examples and problems are worked through, such as finding missing angle measures.