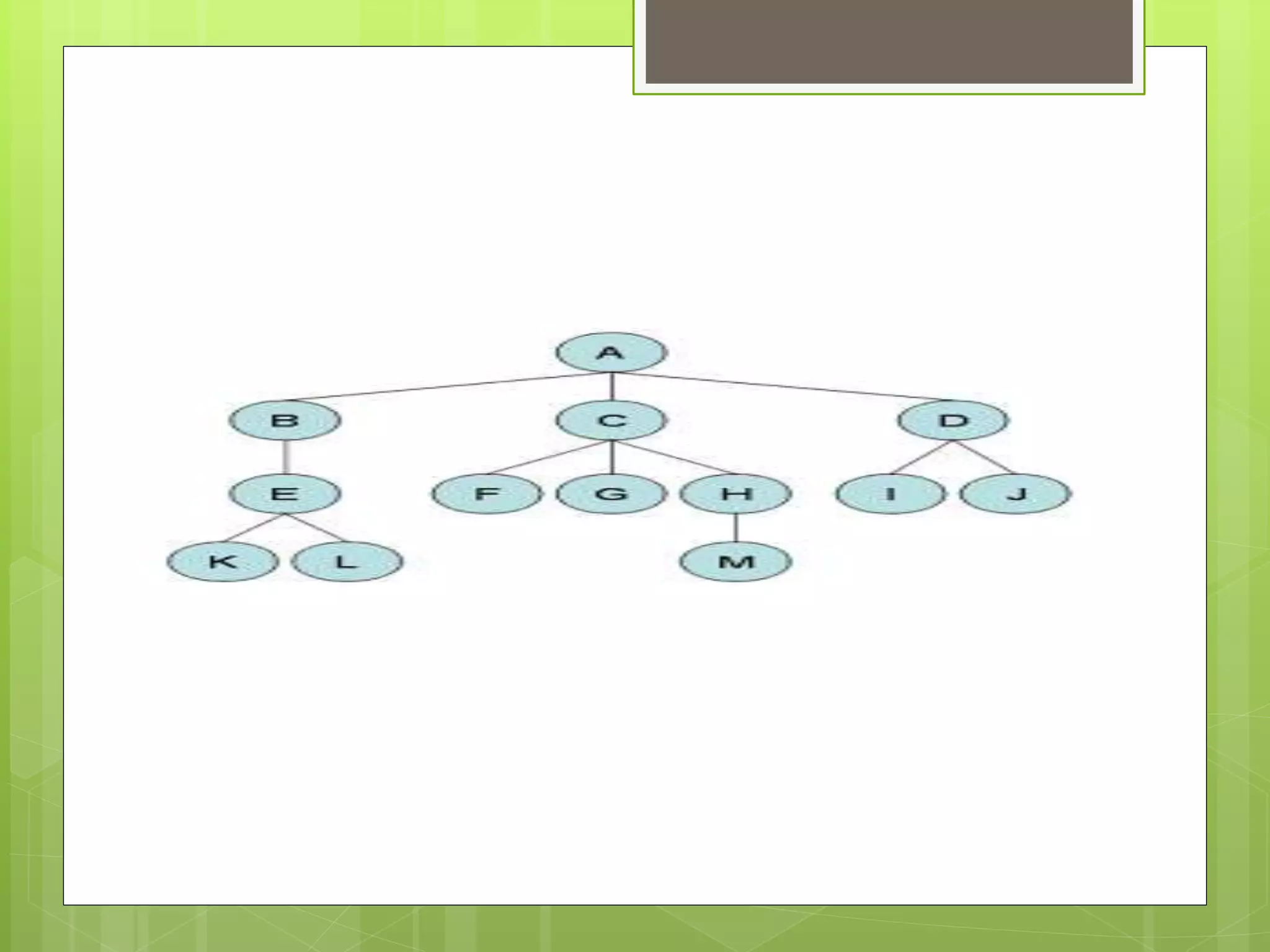
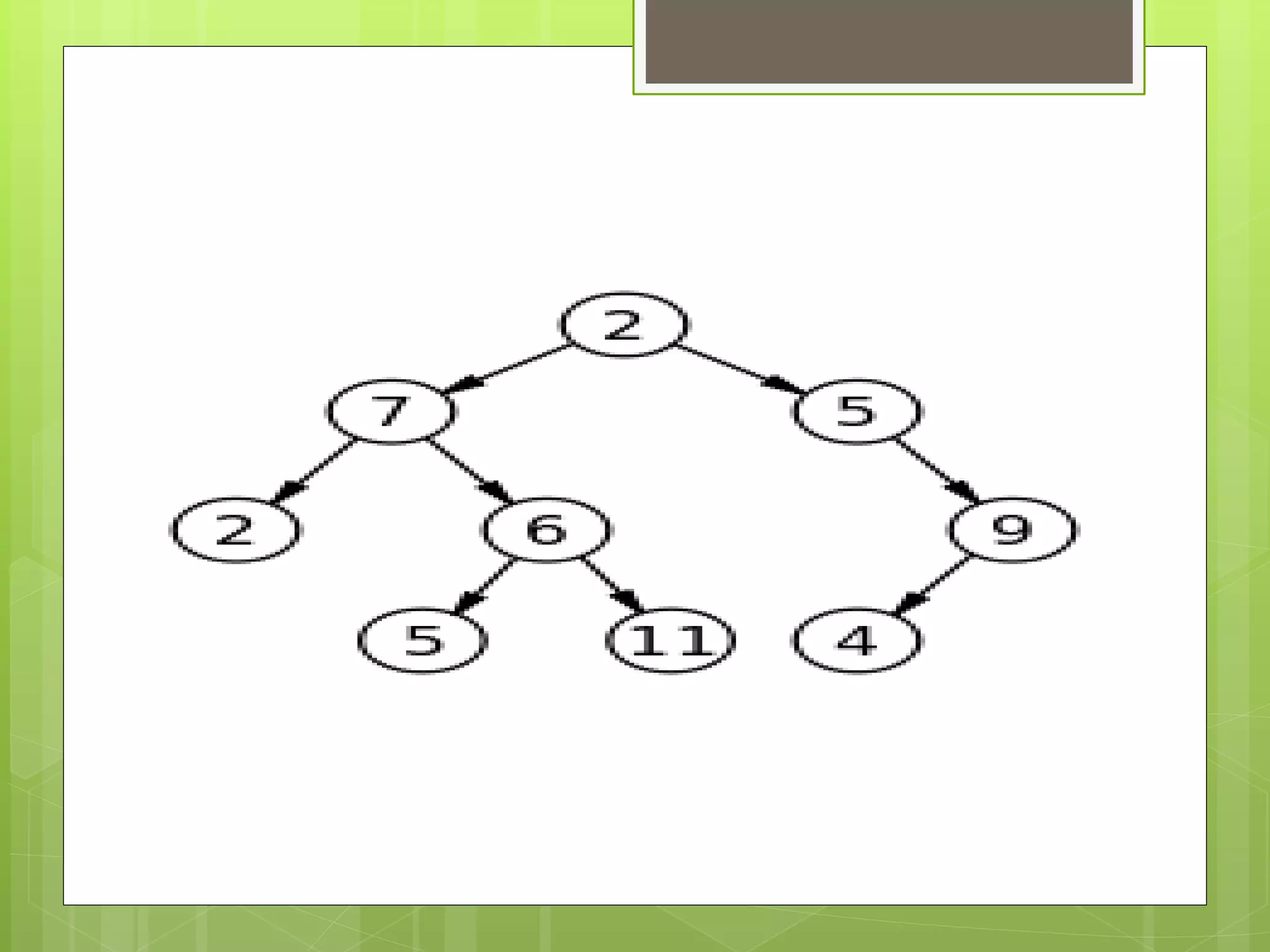
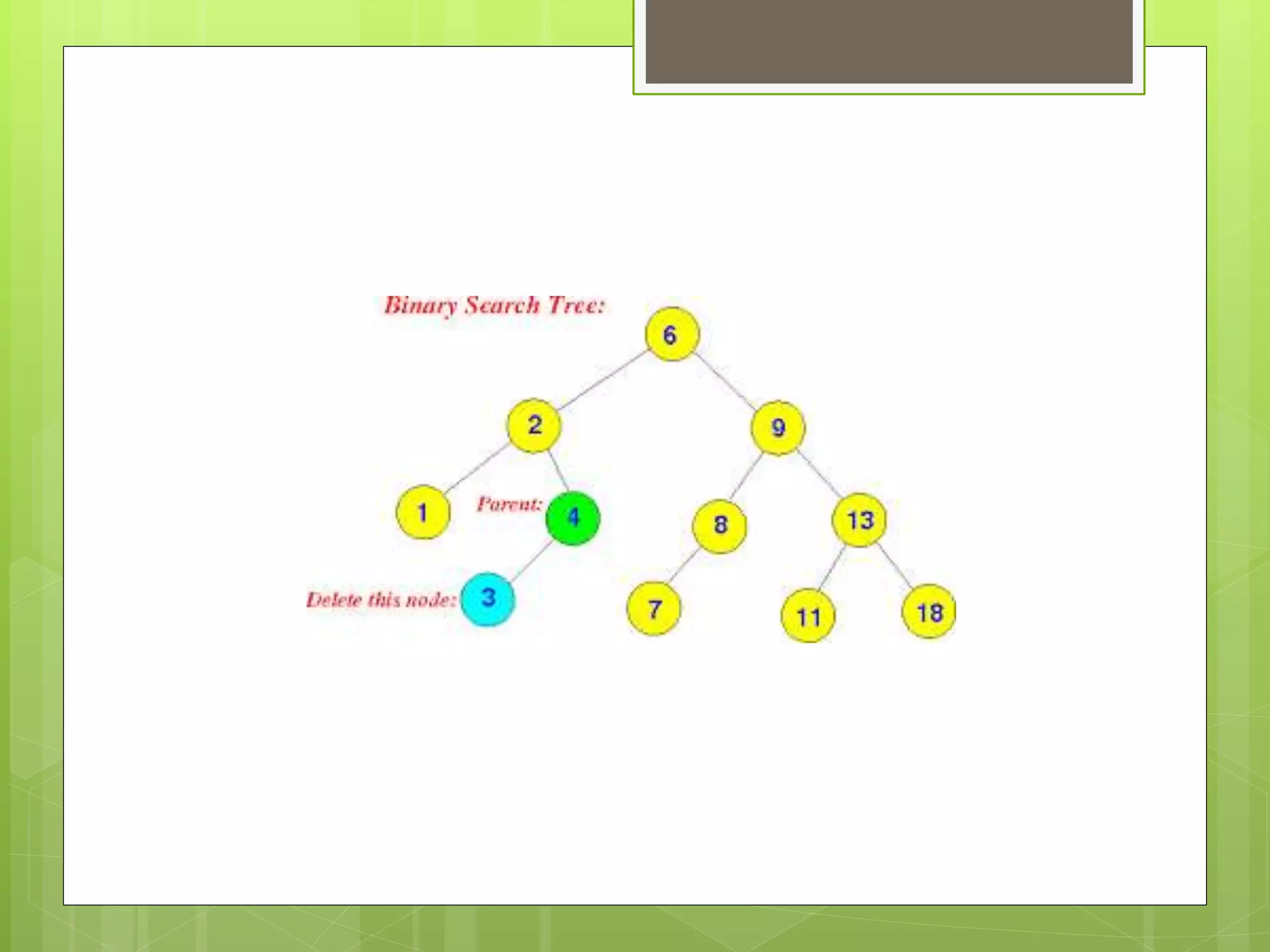
Trees are hierarchical data structures composed of nodes connected by edges. A tree has a root node with child nodes below it. Leaf nodes have no children, while internal nodes have children. Binary trees restrict nodes to having 0, 1, or 2 children. Binary search trees organize nodes so that all left descendants of a node are less than or equal to the node and all right descendants are greater than or equal. Common tree operations include insertion, searching, and deletion.

1. Trees

2. Introduction
 Is a non linear data structure.
 Is a hierarchical data structure.
 Is a finite set of nodes.
 Contains a special node called root node.
 All nodes are connecting through an edge.

4. Terminologies…
 Degree of a Node
Means number of child nodes a node have.
 Leaf
Nodes that have no child nodes.
 Terminal Nodes
Leaf nodes are also called terminal nodes.

5.  Degree of a tree
Maximum degree of tree is called degree of
tree.
 Ancestors
All the parent nodes of a node till rood node
path called its ancestors.
 Descendants
All the child nodes of a node till leaf node
path called its ancestors.

6.  Generation
All nodes with same level called a generation.
 Height/Depth
Number of levels / Generations .
 Edge
Connecting lines that are used to connect
nodes.

7.  Path
sequence of consective edges from 1 node
to other node.
 Branch
if a path ends at leaf nodes called branch.

8. How to construct tree data
structure.
 We can construct it using Linked List.

9. Binary Tree
 A tree having a property that all nodes should
have minimum 0 nodes or maximum 2 nodes.
>=0 nodes <=2.
 If 0 nodes called empty tree/null tree.

11. Types
1: Full BT
- a tree in which each level is filled
completely.
- non leaf nodes should have left as well as
right child's.
- all the leaf nodes should be at same level.

13. 2: Complete Binary tree
each node must have 2 child's (left and right
as well) except leaf nodes.
3: Incomplete binary tree
tree may violate the property of complete
binary tree.

15. Almost complete binary tree
 A tree having all leaf nodes at last or second
last level called almost complete binary tree.

16. Binary Search Tree
 A binary tree in which minimum value is
placed at the left side of node and maximum
value at right side of node.

17. Operations
 Insertion
 Searching
 Deletion

18. Insertion in BST
 Place first at root node.
 Now compare each node value to decide
whether your coming value will be placed at
right or left side of node.
 Takes O(n) in worst case
 Takes Big-Theta (log n) in average case.

19. Searching
 Compare the target value by moving from one
node to other starting from root node.
 Move left if targeted value is smaller than
node value else move right.
 Takes O(n) in worst case
 Takes Big-Theta (log n) in average case.

20. Deletion
 Cases
 If the node is leaf
 If node in non-leaf and have 1 child node.
 If node is non-leaf and have 2 child nodes.

21. If the node is leaf
 Delete that node and make its father node
pointing to Null.
 Left pointer in case of left leaf
 Right pointer in case of right leaf

22. If node is non-leaf and having 1
child node.
 If deleted node is right child of its parent
 Delete the node.
 If have right child or Left Child
 Make it the Right child of deleted node’s
parent.

23.  If deleted node is left child of its parent
 Delete the node.
 If have right child or Left Child
 Make it the left child of deleted node’s
parent.