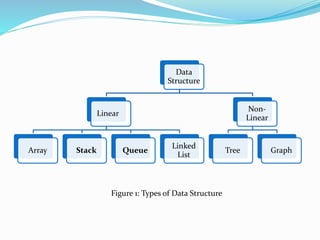
This document discusses different types of data structures, including linear and non-linear structures. It focuses on linear structures like arrays, stacks, and queues. Stacks follow LIFO principles with push and pop operations. Queues follow FIFO principles with enqueue and dequeue operations. Real-world examples and algorithms for common stack and queue operations are provided.

1. Prepared By:
Dr. Chandan Kumar
Assistant Professor, Computer Science & Engineering
Department
Invertis University, Bareilly

2. Data
Structure
Linear
Array Stack Queue
Linked
List
Non-
Linear
Tree Graph
Figure 1: Types of Data Structure

3. Data Structure
 It is a way to arrange a data in a computer ; so that data
can be used effectively
 Data Structure is categorized into two groups in
computer science
 Linear Data Structure
 Non-linear Data Structure

4. Linear Data Structure
 Data items are organized linearly or sequentially
 Data elements attached one after another
 Traversing is done one after another
 Only one element can be directly reached while
traversing
 Implementation of these type data structure is very
easy (Because Computer memory is also organized in
sequential manner)
 Time complexity of linear data structure often
increases with increase in size.

5. Stack
 A stack is a linear data structure that works on the
principal of LIFO (Last-in-First-out)
 Mainly two operations are performed
 push - inserting an item onto
 Pop - deleting or removing an item from the stack
 To maintain stack only one pointer is used and called
TOS( Top of Stack) or TOP (Top of Pointer)
 i.e. accessible at only one end of the sequence

6. Stack
 A stack can be implemented by means of Array,
Structure, Pointer, and Linked List.
 Stack can either be a fixed size one or it may have a
sense of dynamic resizing.

7. Some Real life examples of stack
 A stack of books
 A stack of coins
 A stack of plates

8. Operations performed on stack
Figure 2: push & pop operations

9. PUSH operation
 Used to insert or add an element or an item onto top of the
stack
 Putting a new element onto stack called push operation
 A series of steps involved in push operation
 Step 1 − Checks if the stack is full.
 Step 2 − If the stack is full, produces an error and exit.
 Step 3 − If the stack is not full, increments top to point next
empty space.
 Step 4 − Adds data element to the stack location, where top is
pointing.
 Step 5 − Returns success.

10. PUSH operation representation
Figure 3: push operation representation

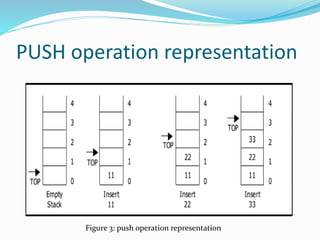
11. PUSH operation Algorithm
1. Insertion(a,top,item,max)
2. If top=max then
 print ‘STACK OVERFLOW’
 exit else
3. top=top+1 end if
4. a[top]=item
5. Exit

12. POP operation
 Used to delete or remove an element or an item from
top of the stack
 Removing an element from stack called pop operation
 A series of steps involved in pop operation
 Step 1 − Checks if the stack is empty.
 Step 2 − If the stack is empty, produces an error and
exit.
 Step 3 − If the stack is not empty, accesses the data
element at which top is pointing.
 Step 4 − Decreases the value of top by 1.
 Step 5 − Returns success.

13. POP operation representation
Figure 4: pop operation representation

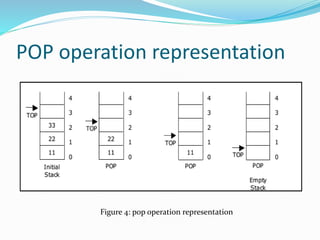
14. POP operation Algorithm
1. Deletion(a,top,item)
2. If top=0 then
print ‘STACK UNDERFLOW’
exit else
3. item=a[top] end if
4. top=top-1
5. Exit

15. Applications of stack
 Used by compiler to check brackets, parenthesis and
braces for balance
 In expression evaluation, such as to evaluate prefix,
postfix and infix expressions.
 Also used in expression conversions
 In recursion all intermediate arguments and return
values will be stored on the stack of the processor.
 The return address and arguments are placed onto a
stack during a function call, and they popped off upon
return.

16. Queue
 It is an abstract data type (ADT) data structure like
stack
 queue is based on FIFO (First-in-First-out) principal.
 Unlike stacks, a queue is open at both its ends
 Two operations are performed
 enqueue or insertion- insert an element
 dequeue or deletion – delete an element
 To maintain queue two pointers are used
 Front
 Rear

17. Queue
 Placing an object in a queue is referred to as
"insertion or enqueue" at the end of the queue
called "rear."
 Removing an object from a queue is referred to as
"deletion or dequeue" at the other end of the queue
called "front“.

18. Some real life example of queue
 Waiting in line

19. Operations performed on queue
Figure 5: Enqueue & Dequeue operations

20. Enqueue operation
 Used to insert element at the end of the queue i.e. rear
 This operation is used to insert an element in a queue at
rear end.
 Following steps are involved to insert an element
 Step 1 − Check if the queue is full.
 Step 2 − If the queue is full, produce overflow error and exit.
 Step 3 − If the queue is not full, increment rear pointer to
point the next empty space.
 Step 4 − Add data element to the queue location, where the
rear is pointing.
 Step 5 − return success.

21. Enqueue operation representation
Figure 6: Enqueue operation representation

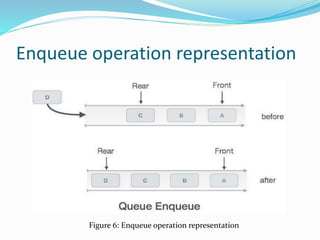
22. Enqueue operation Algorithm
if (rear = maxsize-1 )
print (“queue overflow”) and return
Else
rear = rear + 1 Queue [rear] =
item

23. Dequeue operation
 Used to delete element at the start of the queue i.e. front
 This operation is used to remove an element from a queue
at front end.
 Following steps are involved to insert an element
 Step 1 − Check if the queue is empty.
 Step 2 − If the queue is empty, produce underflow error and
exit.
 Step 3 − If the queue is not empty, access the data
where front is pointing.
 Step 4 − Increment front pointer to point to the next
available data element.
 Step 5 − Return success.

24. Dequeue operation representation
Figure 7: Dequeue operation representation

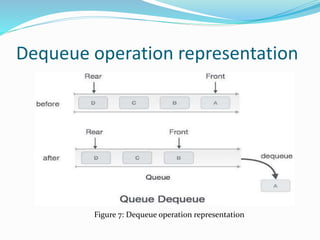
25. Dequeue operation Algorithm
If (front =rear)
print “queue empty” and return
Else
Front = front + 1
item = queue [front];
Return item

26. Applications of Queue
 It is used to schedule the jobs to be processed by the
CPU.
 When several users submit print jobs to a printer,
each print job is kept in the queue for printing.
 Breadth first search (BFS) uses a queue data structure
to find an element from a graph.
 Key board buffering
 Round Robin scheduling