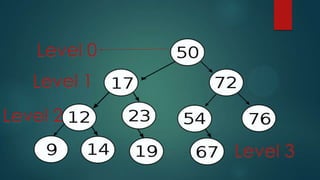
This document defines and describes trees and graphs as non-linear data structures. It explains that a tree is similar to a linked list but allows nodes to have multiple children rather than just one. The document defines key tree terms like height, ancestors, size, and different types of binary trees including strict, full, and complete. It provides properties of binary trees such as the number of nodes in full and complete binary trees based on height.

1. Trees & Graphs
WHAT IS A TREE?
• TREE IS A DATA STRUCTURE SIMILAR TO LINKED LIST
• INSTEAD OF POINTING TO ONE NODE EACH NODE CAN POINT TO A
NUMBER OF POINT
• NON LINEAR DATA STRUCTURE
• WAY OF REPRESENTING HIERARCHAL NATURE OF A STRUCTURE IN A
GRAPHICAL FORM

2. Level 0
Level 1
Level 2
Level 3

3. Some Definition
• HEIGHT OF A NODE IS THE LENGTH OF THE PATH FROM THAT NODE TO
THE DEEPEST NODE. SIMILARLY HEIGHT OF A TREE IS THE LENGTH FROM
ROOT TO THE DEEPEST NODE IN THE TREE. FOR EXAMPLE FOR NODE 17
HEIGHT WOULD BE 2 AND HEIGHT OF THE TREE WOULD BE 4
• ANCESTOR -IF THERE EXISTS A PATH FROM ROOT TO THE NODE LET SAY
Q AND NODE P IS EXIST IN THAT PATH THEN WE CAN CALL P WOULD BE
THE ANCESTOR OF Q.50,70,12 ARE THE ANCESTOR OF 9
• SIZE OF A NODE IS THE NUMBER OF DESCENDENT IT HAS INCLUDING
ITSELF. 72 HAS SIZE = 3
• SKEW TREE – EVERY NODE HAS ONLY ONE CHILD EXCEPT LEAF NODE
• BINARY TREE ---- EACH NODE HAS ZERO CHILD, ONE CHILD OR TWO
CHILD

4. Types of binary tree
STRICT BINARY TREE
• EACH NODE HAS EXACTLY TWO OR ZERO CHILD
FULL BINARY TREE
• EACH NODE HAS EXACTLY TWO NODE OR ZERO CHILD AND LEAF
NODE IS AT THE SAME LEVEL
COMPLETE BINARY TREE
• ALL LEAF NODE IS AT THE HEIGHT OF H OR H-1 AND ALSO WITHOUT
ANY MISSING NODE IN THE SEQUENCE

5. Properties of binary tree
• THE NUMBER OF NODE IN A FULL BINARY TREE ARE 2POW(H+1) – 1.
• THE NUMBER OF NODES IN A COMPLETE BINARY TREE ARE IN BETWEEN
2POW(H) TO 2POW(H+1) – 1.