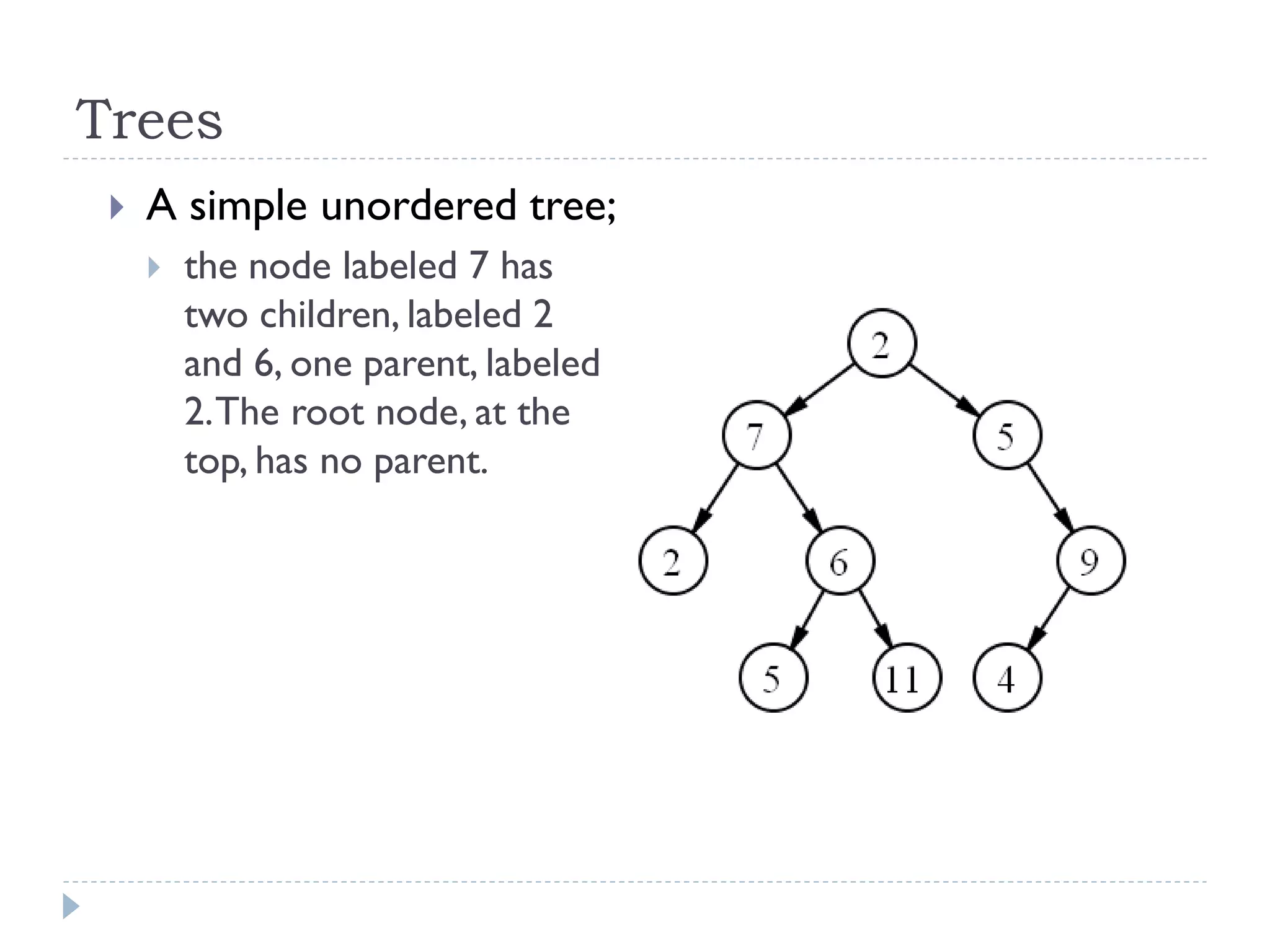
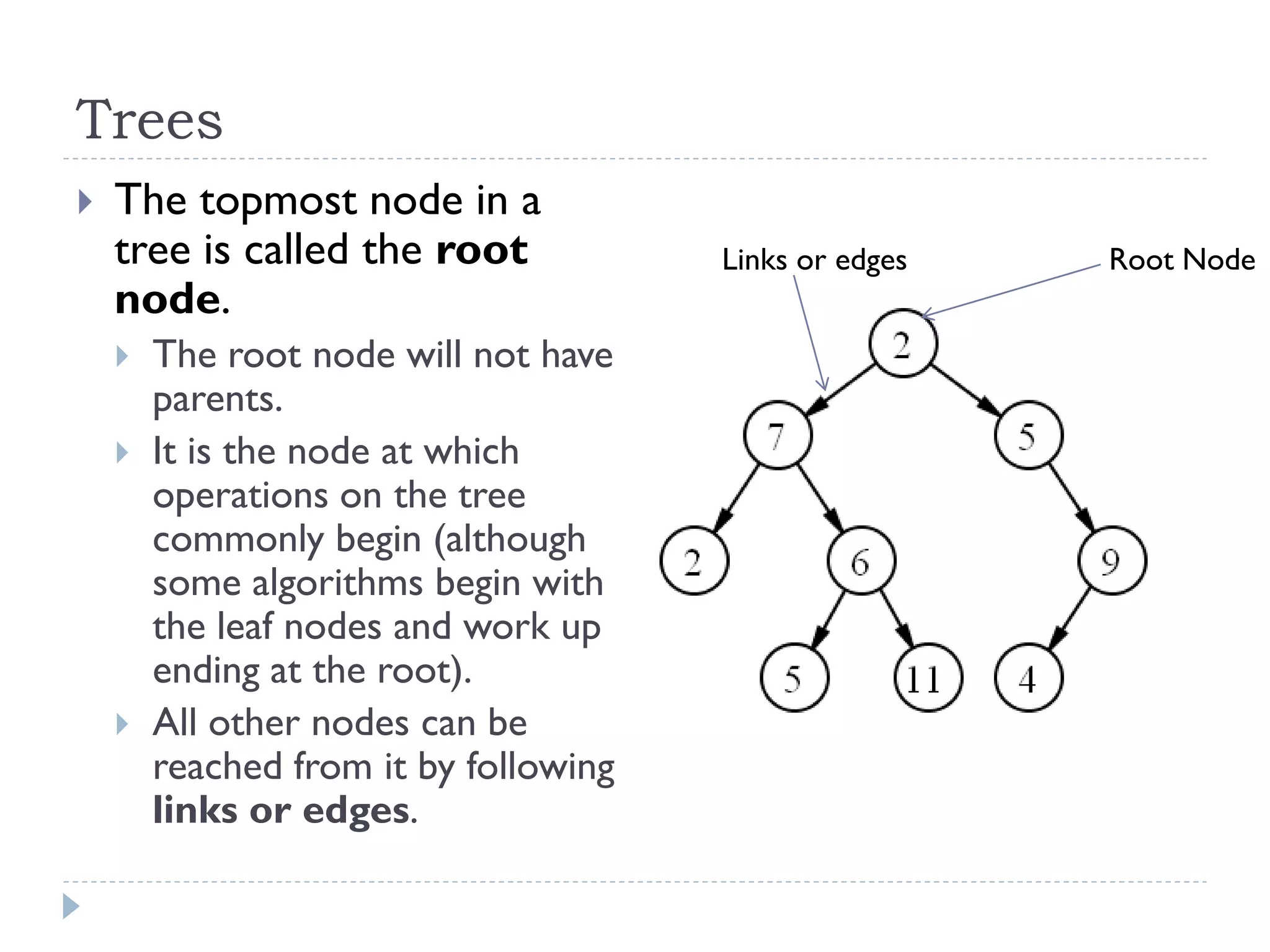
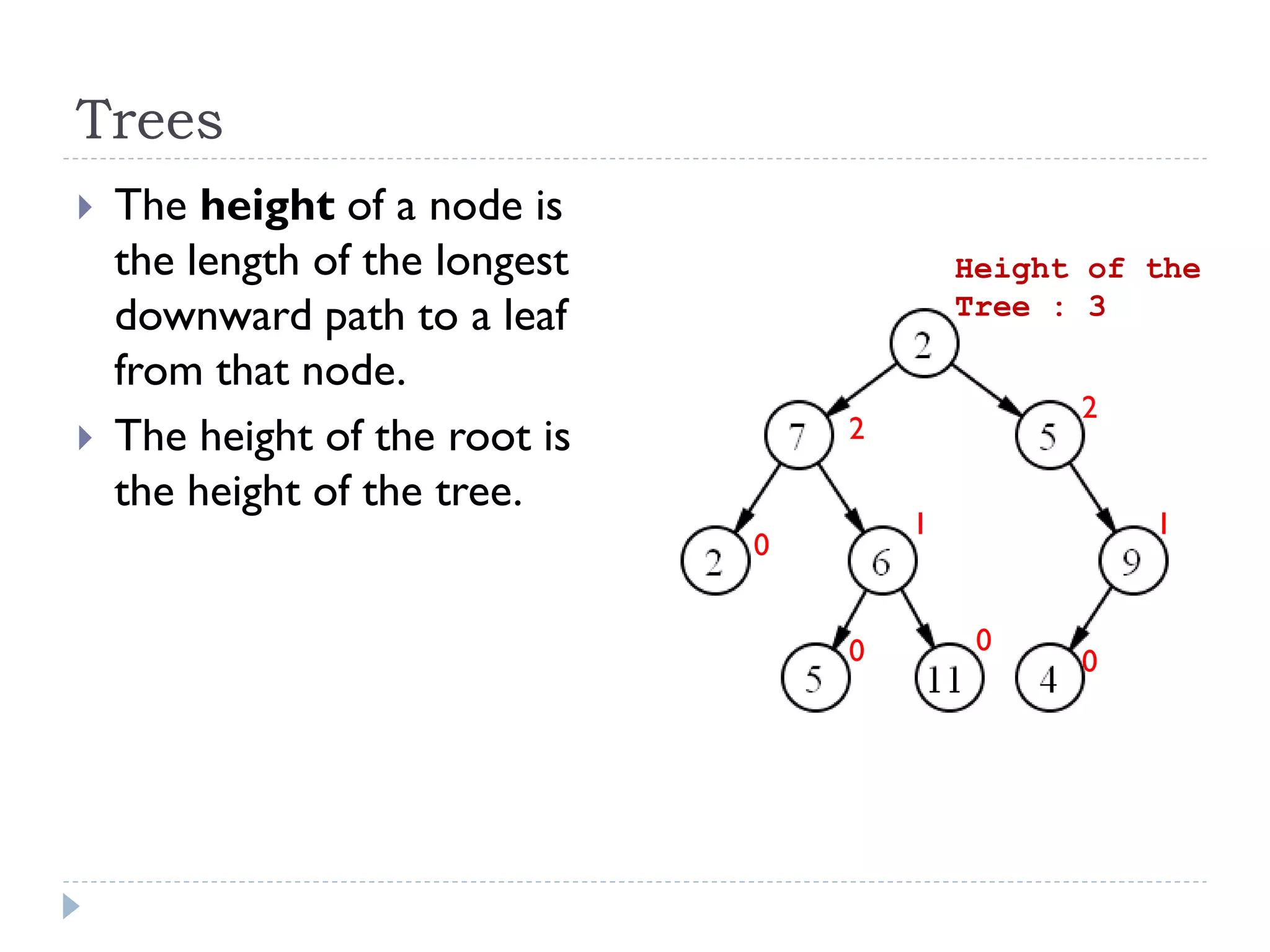
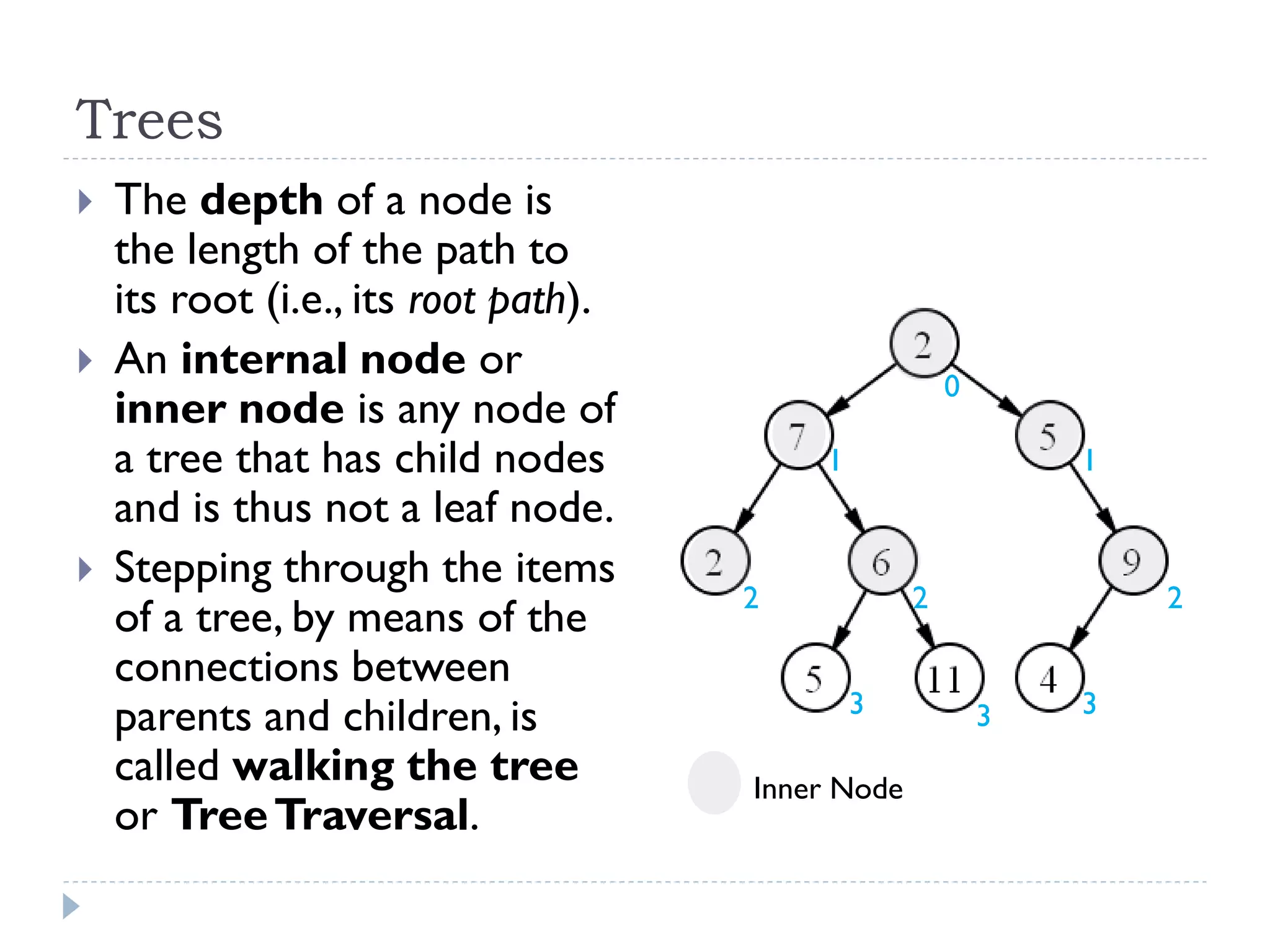
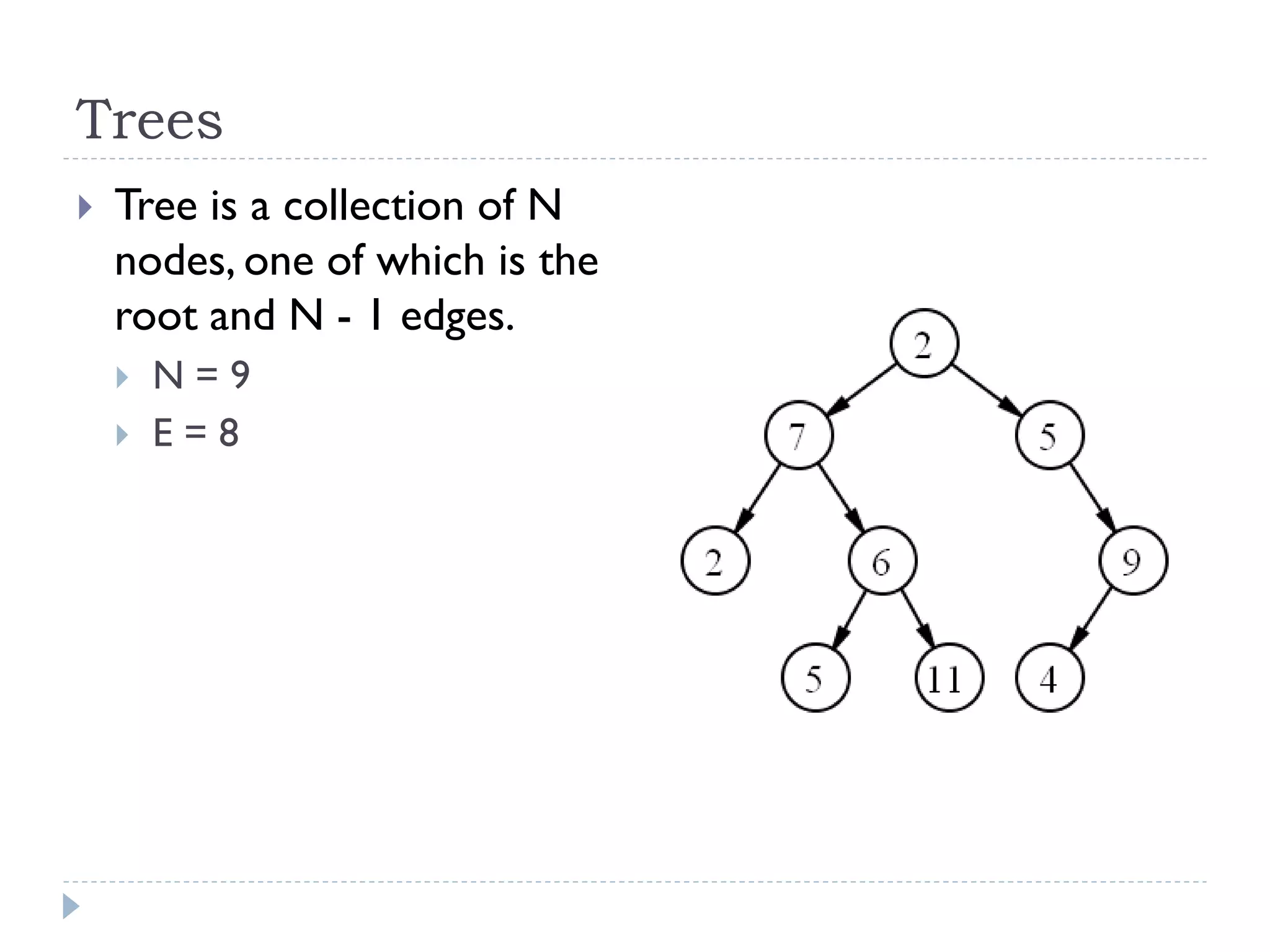
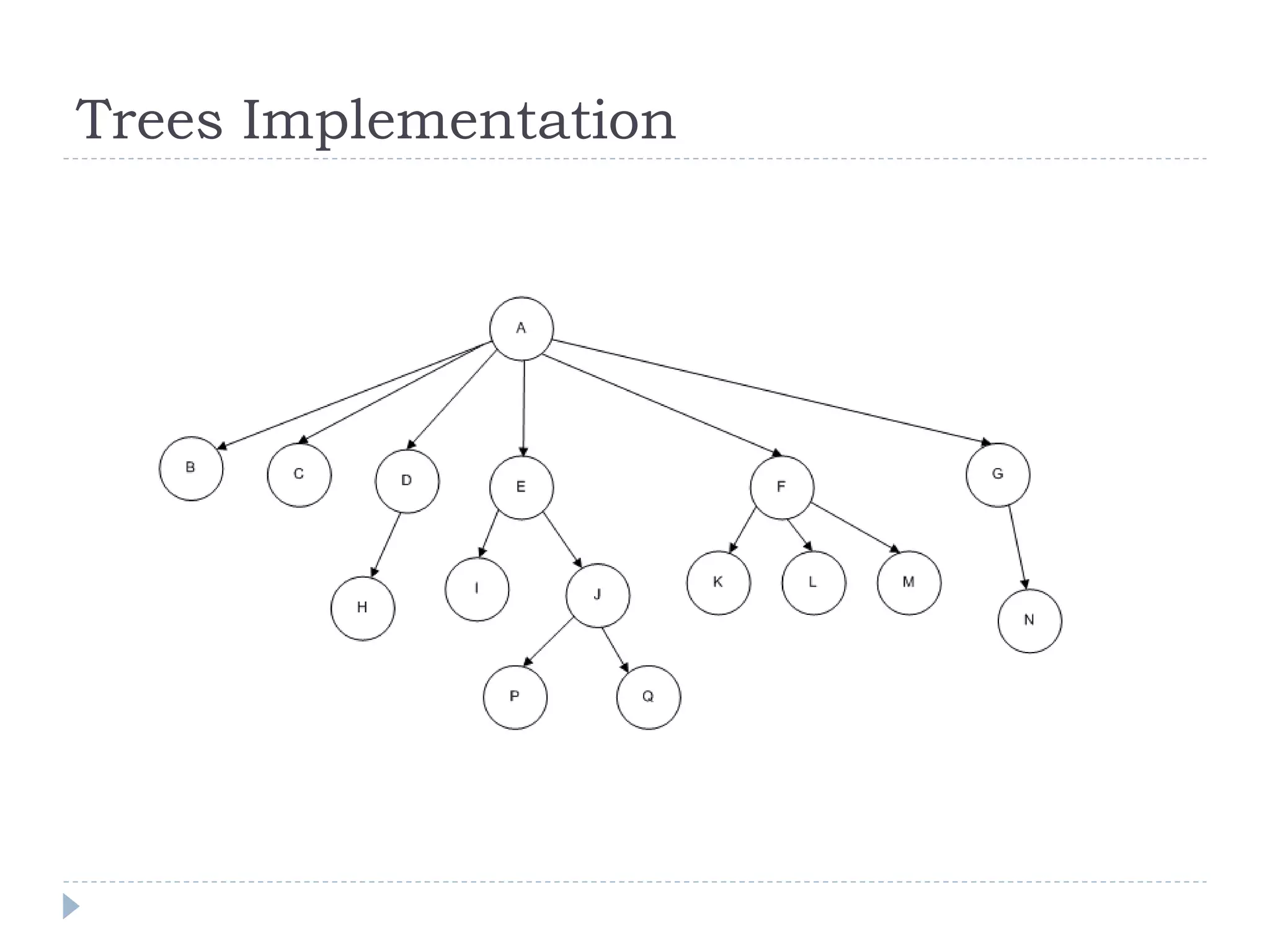
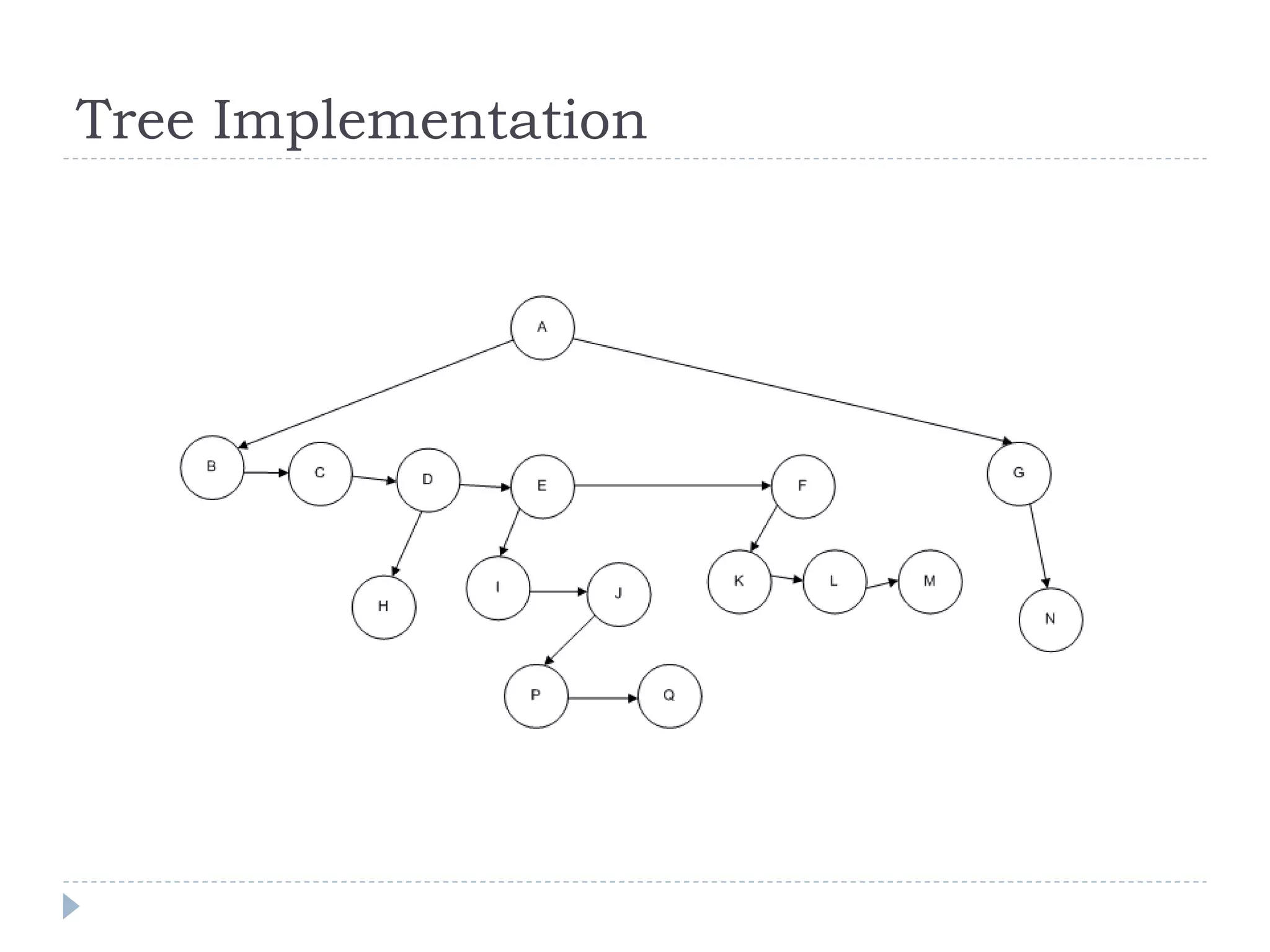
The document outlines the fundamental concepts surrounding trees as a data structure, emphasizing their hierarchical nature with parent-child relationships and node characteristics. It describes the implementation details and traversals of trees, specifically focusing on how nodes are connected, and how data is structured within them. Key terminologies such as root node, internal nodes, leaf nodes, height, and depth are also defined.

1. CS221A – Data Structures &
Algorithms
Trees

2. Agenda
 Trees Concepts and Preliminaries
 Tree Implementation
 TreeTraversal

3. Trees
 An ADT that can store data hierarchically.With a parent
child relationship.
 Widely-used data structure that emulates a hierarchical
tree structure with a set of linked nodes.
 It is a connected graph where each node has a set of zero
or more children nodes, and at most one parent node.

4. Trees
 Node is a structure which may contain a value, a
condition, or represent a separate data structure (which
could be a tree of its own).
 Each node in a tree has zero or more child nodes, which are
below it in the tree (by convention, trees grow down, not up as
they do in nature).
 A node that has a child is called the child's parent node (or
ancestor node, or superior).
 A node has at most one parent.
 Nodes that do not have any children are called leaf nodes.
They are also referred to as terminal nodes.

5. Trees
 A simple unordered tree;
 the node labeled 7 has
two children, labeled 2
and 6, one parent, labeled
2.The root node, at the
top, has no parent.

6. Trees
 The topmost node in a
tree is called the root
node.
 The root node will not have
parents.
 It is the node at which
operations on the tree
commonly begin (although
some algorithms begin with
the leaf nodes and work up
ending at the root).
 All other nodes can be
reached from it by following
links or edges.
Root NodeLinks or edges

7. Trees
 The height of a node is
the length of the longest
downward path to a leaf
from that node.
 The height of the root is
the height of the tree.
0
1
2
Height of the
Tree : 3
00
1
2
0

8. Trees
 The depth of a node is
the length of the path to
its root (i.e., its root path).
 An internal node or
inner node is any node of
a tree that has child nodes
and is thus not a leaf node.
 Stepping through the items
of a tree, by means of the
connections between
parents and children, is
called walking the tree
or TreeTraversal.
3
1
2
33
1
2
0
2
Inner Node

9. Trees
 Tree is a collection of N
nodes, one of which is the
root and N - 1 edges.
 N = 9
 E = 8

10. Trees Implementation

11. Tree Implementation

12. Trees Implementation
 Each Node Maintains Data and a pointer to each of its
child nodes.
 As Number of Children per Node is an unknown , we
keep the children of each node in a linked list of tree
nodes.

13. Tree Implementation
 typedef struct TreeNode *PtrToNode;
 struct TreeNode
 {
 ElementType Element;
 PtrToNode FirstChild;
 PtrToNode NextSibling;
 }

14. Tree Implementation
 voidTraverse(Tree t)
 {
 printf (tElement);
 if (tFirstChild != Null)
 Traverse(tFirstChild);
 if (tNextSibling !=Null)
 Traverse(tNextSibling);
 }