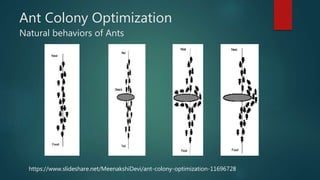
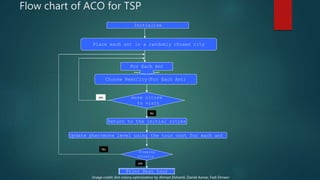
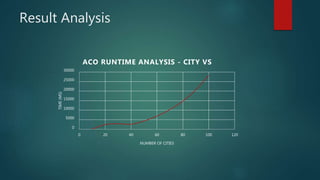
This document discusses using ant colony optimization to solve the travelling salesman problem. It first defines the travelling salesman problem as finding the shortest route for a salesman to visit all cities exactly once and return to the starting city with the minimum cost. It then explains that ant colony optimization is a probabilistic technique inspired by how real ants find food sources, and involves artificial ants laying pheromone trails between cities to probabilistically build solutions. The document provides pseudocode of the ant colony optimization algorithm and shows its results are faster than brute force solutions for solving the travelling salesman problem, with runtime scaling better as the number of cities increases.

1. Travelling and Salesman Problem
Using Ant colony optimization
AKASH SETHIYA
ALGORITHMS FOR ARTIFICIAL INTELLIGENCE (SPRING 2017)
COMPUTER SCIENCE GRADUATE
MISSISSIPPI STATE UNIVERSITY

2. TSP (Travelling and Salesman)
 One salesman, visiting all cities in a route exactly once and come back to
same city where he started.
 Problem to find the path for salesman in which cost is minimum.
 TSP can be modelled as an undirected weighted graph, in which cities are
represent by vertices and path’s are graph edges and distance between
cities are edge weights.
 The goal in TSP is to find a minimum length Hamiltonian circuit of the
graph
 NP-hard problem (Permutation problem)

3. ACO (Ant colony optimization)
 Probabilistic technique for solving computation problem which can be
reduced to finding shortest path through graphs.
 Initially proposed by Marco Dorigo in 1992 in his PhD thesis.
 Inspired by the approach of real ants to find the shortest path from nest to
food source.
 Ants communicate with each other via a chemical substance called
Pheromone.
 Trail which has high amount of pheromone, other ants follow the same
trail to find food otherwise use a random path to search for food source.

4. Ant Colony Optimization
Natural behaviors of Ants
https://www.slideshare.net/MeenakshiDevi/ant-colony-optimization-11696728

5. Pseudocode of ACO
Loop
Randomly position m artificial ants on n cities
for city=1 to n
for ant=1 to m
{Each ant builds a solution by adding one city after other}
Select probabilistically the next city
Apply local trail updating rule
end for
end for
Apply the global trail updating rule using best ant
Until end condition

6. Flow chart of ACO for TSP
Initialize
Place each ant in a randomly chosen city
Choose NextCity(For Each Ant)
more cities
to visit
For Each Ant
Return to the initial cities
Update pheromone level using the tour cost for each ant
Print Best tour
yes
No
Stopping
criteria
yes
No
Image credit: Ant colony optimization by Ahmad Elshamli, Daniel Asmar, Fadi Elmasri

7. Results
No of Cities Brute Force (TSP) (ms) ACO (TSP) (ms)
10 95.2
20 2407
30 2888.4
40 2609.4
50 4328.8
60 6880.6
70 10345
80 14706
90 20704
100 28313

8. Result Analysis
0
5000
10000
15000
20000
25000
30000
0 20 40 60 80 100 120
TIME(MS)
NUMBER OF CITIES
ACO RUNTIME ANALYSIS - CITY VS

9. Complexities
 TSP – Brute force – O(n!)
 TSP – Dynamic Programming – O(2n n2)
 TSP – ACO - O(mn3)

10. References
 The Ant System: Optimization by a colony of cooperating agents by Marco
Dorigo, Member, IEEE, Vittorio Maniezzo and Alberto Colorni
 An Ant colony optimization Algorithm for Solving Travelling Salesman
Problem, Krishna H. Hingrajiya, Ravindra Kumar Gupta, Gajendra Singh
Chandel
 https://github.com/lukedodd/ant-tsp
 https://en.wikipedia.org/wiki/Ant_colony_optimization_algorithms
 http://www.geeksforgeeks.org/travelling-salesman-problem-set-1/
 https://en.wikipedia.org/wiki/Travelling_salesman_problem

11. THANK YOU