Ant colony optimization is an optimization technique inspired by the behavior of real ant colonies. The technique was introduced in the 1990s and uses indirect coordination between agents through pheromone trails to solve problems. Ants communicate by laying pheromone trails and tend to follow stronger trails, with the result that the paths between food sources emerge from their collective behavior without centralized control. The ant colony optimization algorithm applies this behavior to problems by having artificial "ants" probabilistically build solutions and adjust pheromone levels to guide future construction. The algorithm has been successfully applied to problems like the traveling salesman problem.

1. Ant Colony Optimization
18-02-2014
Ant Colony Optimization
1

2. Ant Colony Optimization
Ant colony optimization is a technique for
optimization that was introduced in the early 1990’s.
The inspiring source of ant colony optimization is the
foraging behaviour of real ant colonies.
18-02-2014
Ant Colony Optimization
2

3. Swarm Intelligence
Collective system capable of accomplishing difficult
tasks in dynamic and varied environments without
any external guidance or control and with no central
coordination
Achieving a collective performance which could not
normally be achieved by an individual acting alone
Constituting a natural model particularly suited to
different kind of problem solving
18-02-2014
Ant Colony Optimization
3

4. Swarm Algorithms
Inspiration from swarm intelligence has led to
some highly successful optimization algorithms.
One of those algorithms is …..
Ant Colony algorithm – a way to solve optimization
problems based on the behaviour of ants searching for
food.
18-02-2014
Ant Colony Optimization
4

5. A key concept: Stigmergy
Stigmergy is:
indirect coordination between agents or actions.
 The
principle is that the trace left in
the environment by an action stimulates the
performance of a next action, by the same or a
different agent.
 Individuals
leave markers or messages – these don’t
solve the problem in themselves, but they affect other
individuals in a way that helps them solve the
problem
18-02-2014
Ant Colony Optimization
5

6. Stigmergy in Ants
Ants are behaviourally unsophisticated, but
collectively they can perform complex tasks.
Ants have highly developed sophisticated signbased stigmergy
They communicate using pheromones
They lay trails of pheromone that can be
followed by other ants.
18-02-2014
Ant Colony Optimization
6

7. Pheromone Trails
One ant tends to follow strong concentrations
of pheromone caused by repeated passes of ants; a
pheromone trail is then formed from nest to food
source,
so in intersections between several trails an ant moves
with high probability following the highest
pheromone level.
18-02-2014
Ant Colony Optimization
7

8. Pheromone Trails continued
Individual ants lay pheromone trails while
travelling from the nest, to the nest or possibly in
both directions.
The pheromone trail gradually evaporates over
time.
…But pheromone trail strength accumulate with
multiple ants using path.
18-02-2014
Ant Colony Optimization
8

9. Pheromone Trails: Example
18-02-2014
Ant Colony Optimization
9

10. Ant Colony Optimization
Algorithms: Basic Ideas
Ants are agents that:
 Move along between nodes in a graph.
 They choose where to go based on pheromone strength (and maybe
other things)
 An ant’s path represents a specific candidate solution.
 When an ant has finished a solution, pheromone is laid on its path,
according to quality of solution.
 This pheromone trail affects behaviour of other ants by `stigmergy’ …
18-02-2014
Ant Colony Optimization
10

11. Travelling Salesman Problem
(TSP)
Given a list of cities and the distances between each
pair of cities, what is the shortest possible route that
visits each city exactly once and returns to the origin
city?
18-02-2014
Ant Colony Optimization
11

12. ACO for the Traveling Salesman Problem
18-02-2014
Ant Colony Optimization
12

13. E.g. A 4-city TSP
Initially, random levels of pheromone are scattered on the edges
A
Pheromone
Ant
18-02-2014
C
AB: 10, AC: 10, AD: 30,
Ant Colony Optimization
B
D
BC: 40, CD: 20
13

14. E.g. A 4-city TSP
An ant is placed at a random node
A
Pheromone
Ant
18-02-2014
B
D
C
AB: 10, AC: 10, AD: 30,
Ant Colony Optimization
BC: 40, CD: 20
14

15. E.g. A 4-city TSP
The ant decides where to go from that node,
based on probabilities
A
calculated from:
- pheromone strengths,
- next-hop distances.
B
Suppose this one chooses BC
Pheromone
Ant
18-02-2014
C
AB: 10, AC: 10, AD: 30,
Ant Colony Optimization
D
BC: 40, CD: 20
15

16. E.g. A 4-city TSP
The ant is now at C, and has a ‘tour memory’ = {B, C} – so he cannot
visit B or C again.
A
B
Again, he decides next hop
(from those allowed) based
on pheromone strength
and distance;
suppose he chooses
CD
Pheromone
Ant
18-02-2014
C
AB: 10, AC: 10, AD, 30,
Ant Colony Optimization
D
BC: 40,
CD: 20
16

17. E.g. A 4-city TSP
The ant is now at D, and has a `tour memory’ = {B, C, D}
There is only one place he can go now:
A
B
Pheromone
Ant
18-02-2014
C
AB: 10, AC: 10, AD, 30,
Ant Colony Optimization
D
BC: 40,
CD: 20
17

18. E.g. A 4-city TSP
So, he has nearly finished his tour, having gone over the links:
BC, CD, and DA.
A
B
Pheromone
Ant
18-02-2014
C
AB: 10, AC: 10, AD, 30,
Ant Colony Optimization
D
BC: 40,
CD: 20
18

19. E.g. A 4-city TSP
So, he has nearly finished his tour, having gone over the links:
BC, CD, and DA. AB is added to complete the round trip.
A
B
Now, pheromone on the tour
is increased, in line with the
fitness of that tour.
Pheromone
Ant
18-02-2014
C
AB: 10, AC: 10, AD, 30,
Ant Colony Optimization
D
BC: 40,
CD: 20
19

20. E.g. A 4-city TSP
A
B
Next, pheromone everywhere
is decreased a little, to model
decay of trail strength over
time
Pheromone
Ant
18-02-2014
C
AB: 10, AC: 10, AD, 30,
Ant Colony Optimization
D
BC: 40,
CD: 20
20

21. E.g. A 4-city TSP
We start again, with another ant in a random position.
A
B
Where will he go?
Next , the actual algorithm
and variants.
Pheromone
Ant
18-02-2014
C
AB: 10, AC: 10, AD, 30,
Ant Colony Optimization
D
BC: 40,
CD: 20
21

22. The ACO algorithm for the TSP
[a simplified version with all essential details]
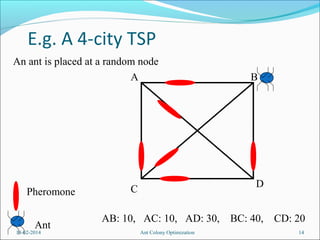
We have a TSP, with n cities.
1. We place some ants at each city. Each ant then does this:

It makes a complete tour of the cities, coming back to its starting
city, using a transition rule to decide which links to follow. By this
rule, it chooses each next-city at random, but biased partly by the
pheromone levels existing at each path, and biased partly by heuristic
information.
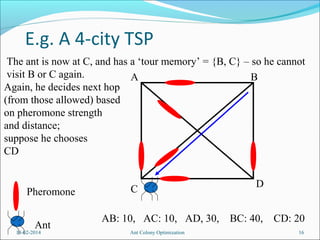
2. When all ants have completed their tours.
Global Pheromone Updating occurs.


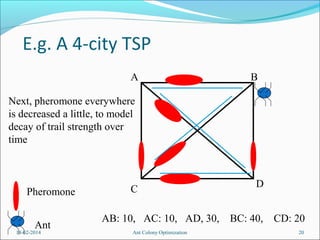
The current pheromone levels on all links are reduced (I.e.
pheromone levels decay over time).
Pheromone is laid (belatedly) by each ant as follows: it places
pheromone on all links of its tour, with strength depending on how
good the tour was.
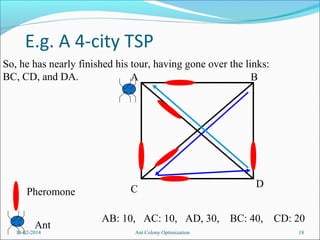
Then we go back to 1 and repeat the whole process many
18-02-2014
Ant Colony Optimization
times, until we reach a termination criterion.
22

23. The transition rule
T(r,s) is the amount of pheromone currently on the path that goes
directly from city r to city s.
H(r,s) is the heuristic value of this link – in the classic TSP
application, this is chosen to be 1/distance(r,s) -- I.e. the shorter
the distance, the higher the heuristic value.
pk (r , s ) is the probability that ant k will choose the link that goes
from r to s
β is a parameter that we can call the heuristic strength
The rule is:
pk ( r , s ) =
T (r , s ) ⋅ H (r , s ) β
β
∑ T (r , c) ⋅ H (r , c)
unvisited cities c
Where our ant is at city r, and s is a city as yet unvisited on its
tour, and the summation is over all of k’s unvisited cities
18-02-2014
Ant Colony Optimization
24

24. Global pheromone update
Ak(r,s) is amount of pheromone added to the (r, s) link by ant k.
m is the number of ants
ρ is a parameter called the pheromone decay rate.
Lk is the length of the tour completed by ant k
T(r, s) at the next iteration becomes:
ρ ⋅ T (r , s) +
m
∑ A (r , s )
k
k =1
Where Ak ( r , s ) = 1 / Lk
18-02-2014
Ant Colony Optimization
25

25. Not just for TSP of course
ACO is naturally applicable to any sequencing
problem, or indeed any problem
All you need is some way to represent solutions to the
problem as paths in a network.
18-02-2014
Ant Colony Optimization
26

26. Other Application of ACO
 Quadratic Assignment Problem
 Network Model Problem
 Vehicle routing
 Feature Selection
 Scheduling Problem
 Vehicle Routing Problem
18-02-2014
Ant Colony Optimization
27

27. Some inherent advantages
Positive Feedback accounts for rapid discovery of
good solutions
Distributed computation avoids premature
convergence
The greedy heuristic helps find acceptable
solution in the early solution in the early stages of
the search process.
The collective interaction of a population of
agents.
18-02-2014
Ant Colony Optimization
28

28. Disadvantages
Slower convergence than other Heuristics
Performed poorly for TSP problems larger than 75
cities.
No centralized processor to guide the system towards
good solutions
18-02-2014
Ant Colony Optimization
29

29. Conclusion
ACO is a thriving and maturing research area – it has
its own conferences. It gets very good results on some
difficult problems.
ACO research and practice tends to concentrate on:
hybridisation with other methods; e.g. it is common
to improve an individual ant’s solution by local
search, and then lay pheromone. New and adaptive
ways to control the relative influence of heuristics,
pheromone strength and pheromone decay.
18-02-2014
Ant Colony Optimization
30

30. References
 https://www.ics.uci.edu/~welling/teaching/271fall09/antcolonyopt.pdf
 rain.ifmo.ru/~chivdan/presentations
 www.macs.hw.ac.uk/~dwcorne/Teaching
 Dorigo M, Optimization, learning and natural algorithms. PhD thesis,
Dipartimento di Elettronica, Politecnico di Milano, Italy, 1992 [in
Italian]
 Wikipedia
 https://www.ics.uci.edu/~welling/teaching/271fall09
 code.ulb.ac.be/dbfiles/
 Ant Colony Optimization for Feature Selection in Software Product
Lines by WANG Ying-lin1,2, PANG Jin-wei2
 mitpress.mit.edu/books/ant-colony-optimization
18-02-2014
Ant Colony Optimization
31

31. 18-02-2014
Ant Colony Optimization
32