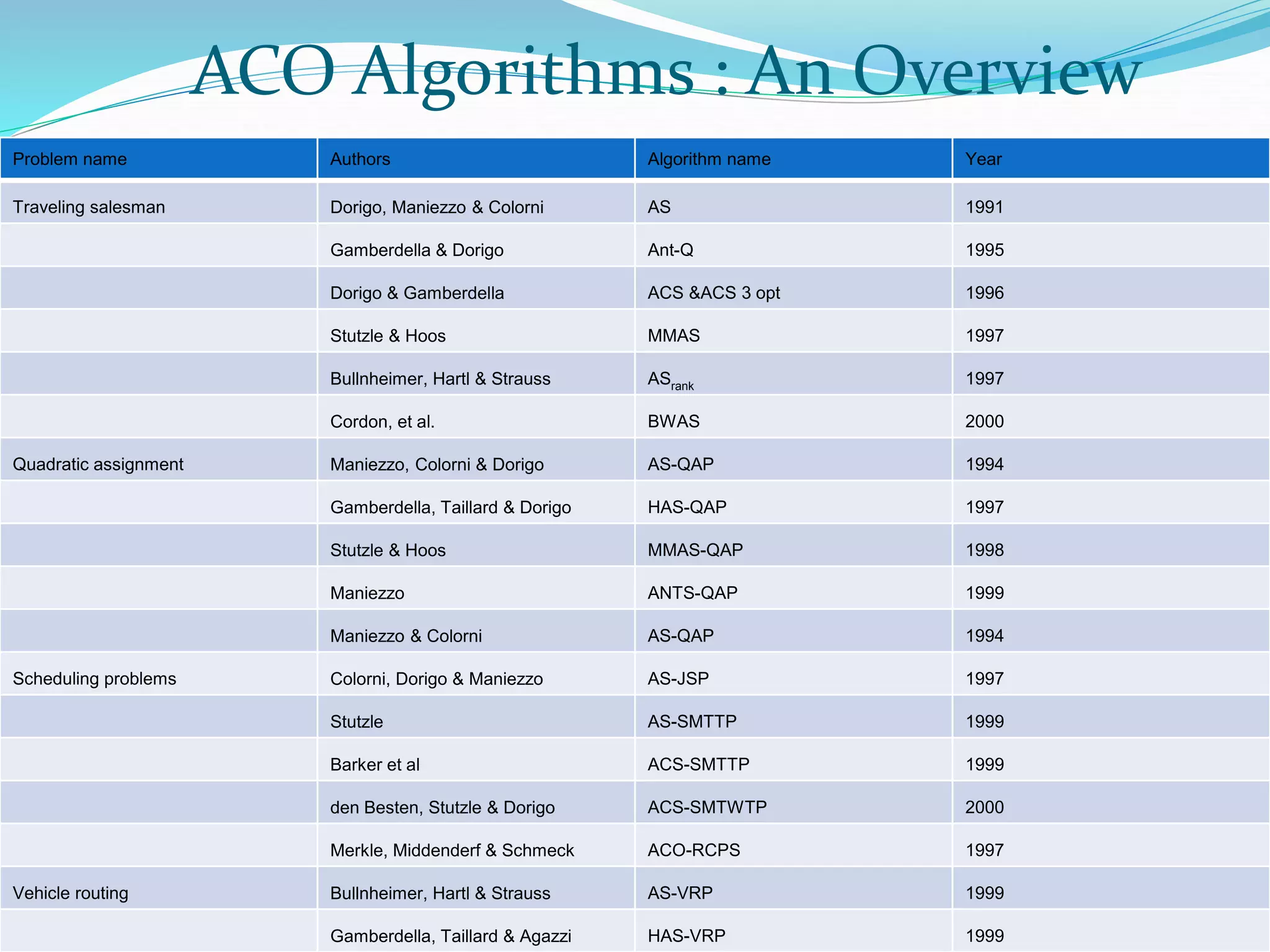
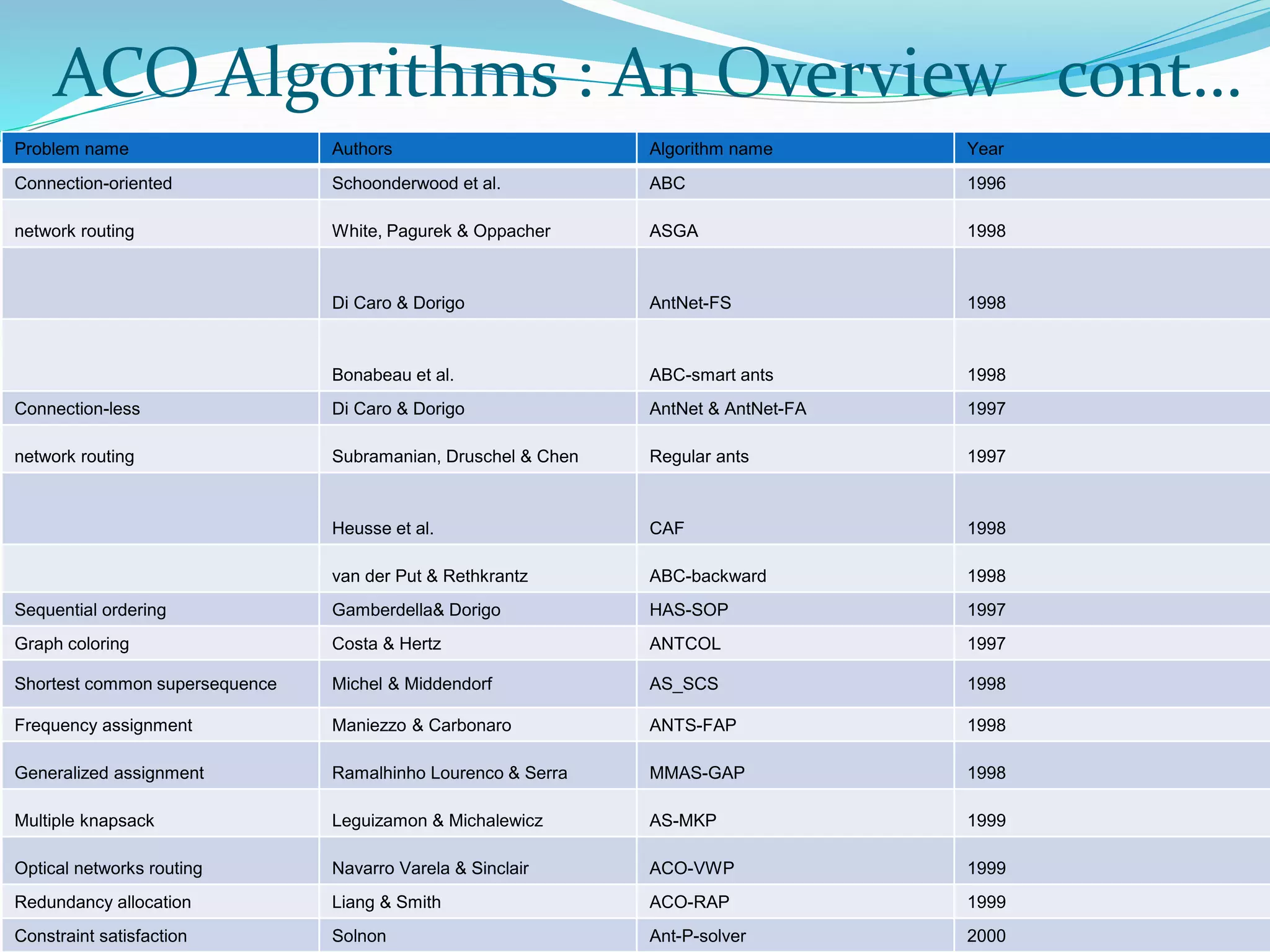
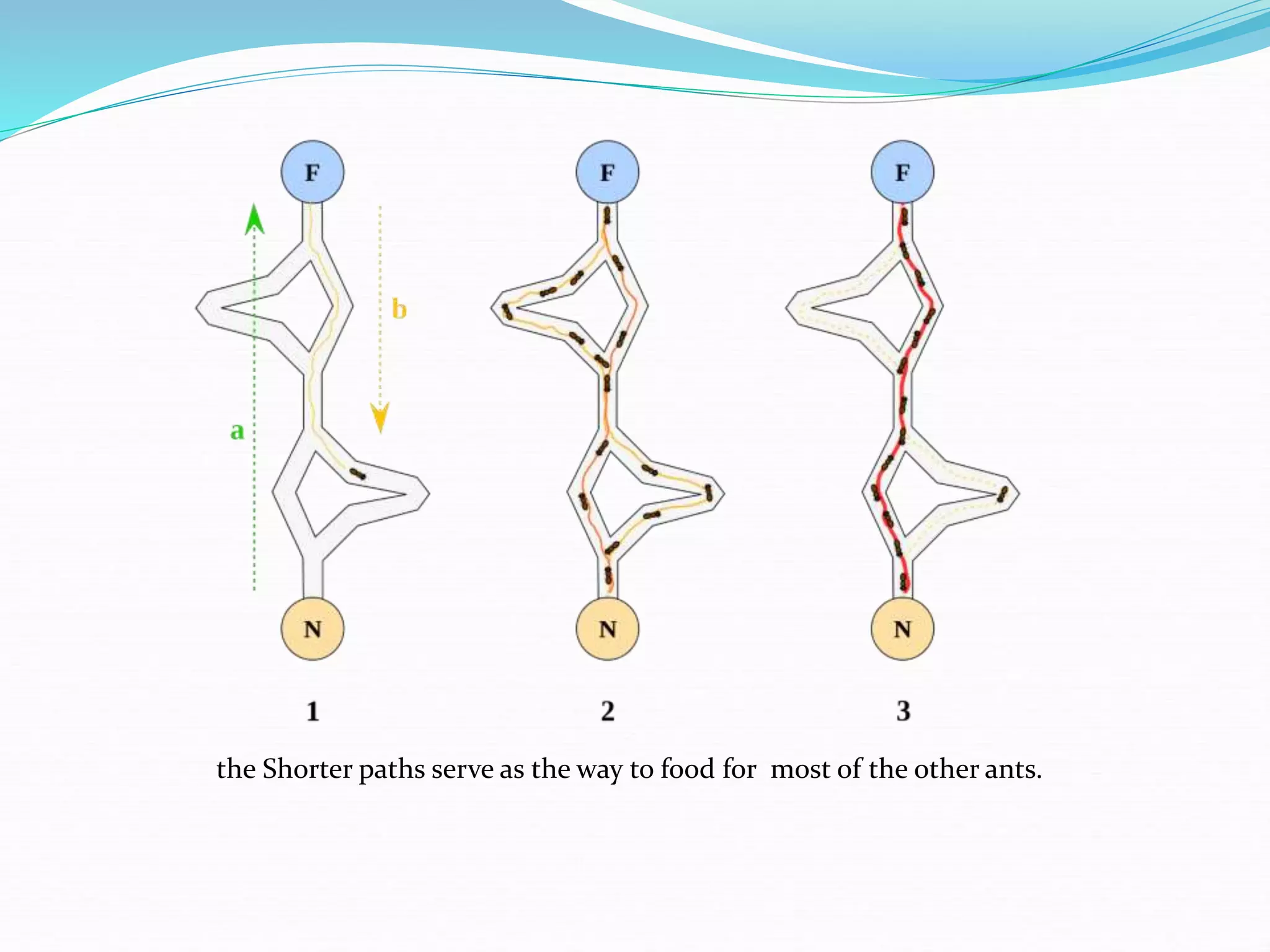
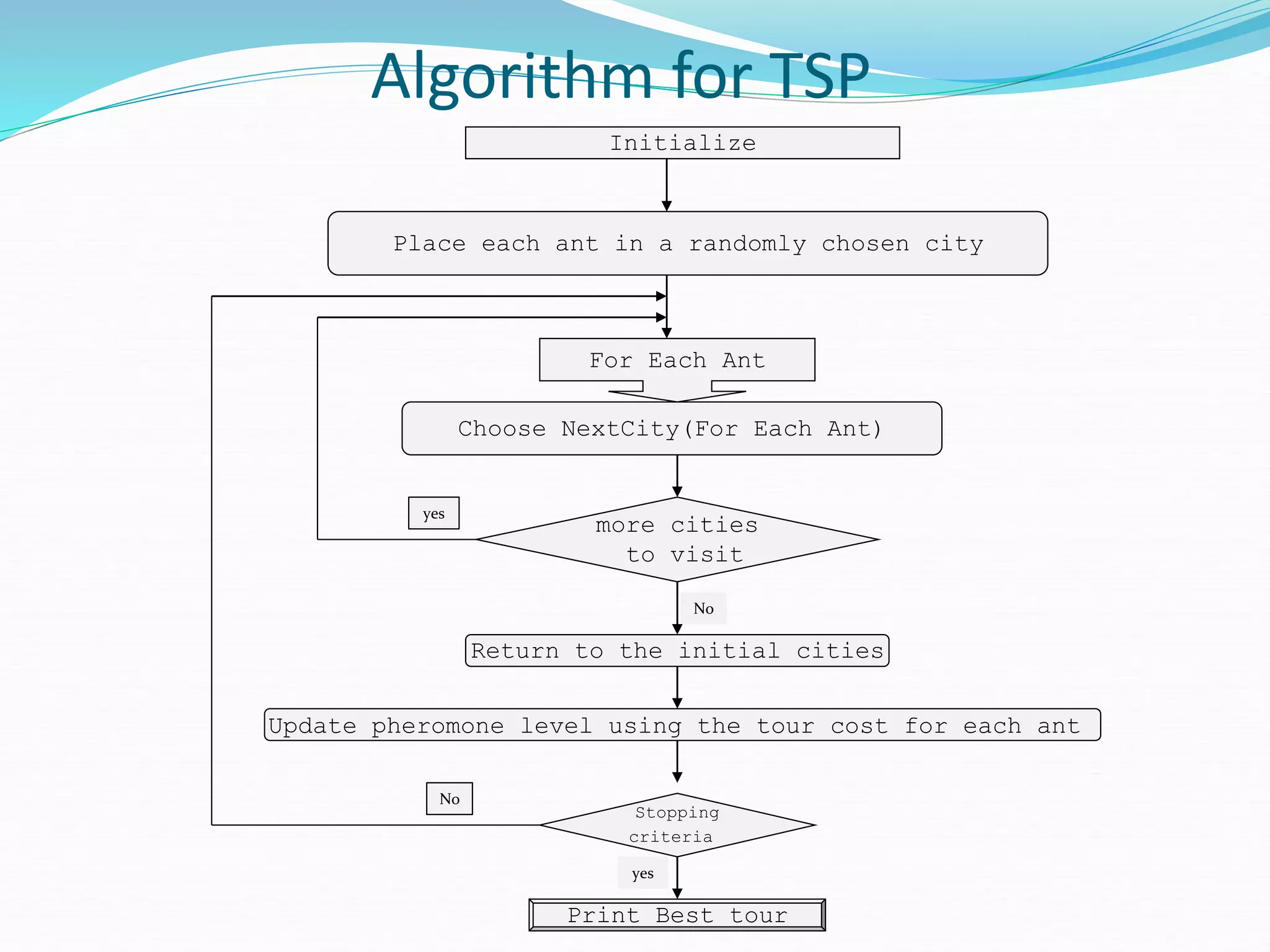
The document discusses ant colony optimization (ACO), which is an algorithm inspired by how ants find food. It describes how ants deposit pheromones to mark shorter paths, reinforcing them. The ACO algorithm simulates this process, with "ants" probabilistically building solutions and updating pheromones. It provides pseudocode and discusses applications to problems like the traveling salesman problem. ACO shows good performance on distributed, combinatorial optimization problems.

1. By,
Name: Suraj Padhy
Roll: S/07/73
Regd.: 0701204232
Branch: CSE

2. Goal of Optimization
Find values of the variables that minimize or maximize the
objective function while satisfying the constraints.
Type of Optimization Techniques
A. Classical Optimization Techniques
B. Numerical Optimization Techniques
C. Advanced Optimization Techniques
 Heuristic
 Greedy Algorithms
 Meta – Heuristic
 Simulated annealing
 Particle swarm optimization
 Ant colony optimization

4. Swarm Intelligence (SI)
 SI is artificial intelligence, based on the collective behavior of
decentralized, self- organized systems.
 The expression was introduced by Gerardo Beni and Jing Wang in
1989, in the context of cellular robotic systems.
 SI systems are typically made up of a population of simple agents
interacting
 locally with one another and with their environment.
 Natural examples of SI include ant colonies, bird flocking, animal
herding, bacterial growth, and fish schooling.

5. Ant Colony Optimization
 First proposed by M. Dorigo, 1992.
 A search technique used in computing to find near optimal
solutions to discrete optimization problems.
 ACO is a swarm intelligence inspired from the way that ants
indirectly communicate directions to each other.

6. Biological inspiration of ants
 The way ants find their food in shortest path is interesting.
 Ants hide pheromones to remember their path.
 These pheromones evaporate with time.
 Whenever an ant finds food , it marks its return journey with
pheromones.
 Pheromones evaporate faster on longer paths
 Shorter paths serve as the way to food for most of the other
ants.
 The shorter path will be reinforced by the pheromones
further.
 Finally , the ants arrive at the shortest path.

7. the Shorter paths serve as the way to food for most of the other ants.

8. Ant Colony Optimization
Key Terms
Ants 𝑘: Any possible solution.
Population 𝑁- Group of all ants.
Search Space [𝑙𝑏,𝑢𝑏]- All possible solutions to the problem.
Search Space is divided by step size ℎ
Pheromone trail 𝜏
Scaling parameter 𝜁
Evaporate rate ρ

9. Ant Colony Optimization
Procedure
 Initialization
Assume a suitable number of ants in the colony
(population 𝑁)
Assume a set of permissible discrete values 𝑚 for each of
the design variables (step size ℎ).
Initialize all discrete values of design variables equal
amounts of pheromone 𝜏.

10. Ant Colony Optimization


11. Ant Colony Optimization
Procedure
 Select Path (solution)
Generate N random numbers r in the range (0, 1), one
for each ant.
Determine the discrete value by ant k for variable as
the one for which the cumulative probability range
includes the random numbers r.
‫اتر‬
‫تالنت‬
‫ال‬

12. Ant Colony Optimization


13. Ant Colony Optimization
Procedure
 Termination
The steps of ACO algorithm are iteratively repeated
until the maximum number of iteration is reached or a
termination criterion is met.
Convergence: is the case where the of all ants converge
to the same set of values, the method is assumed to
have converged.

14. Ant Colony Optimization
Parameters required from user:
Population size 𝑁
Set of permissible discrete values 𝑚 for each of the
design variables
Step size ℎ
Initial pheromone trail 𝜏
Scaling parameter 𝜁
Evaporate rate ρ
Termination criteria (i.e. number of iteration 𝑇)

15. Ant Colony Optimization
Pseudo code
1. Input
Objective function (fitness function), upper bound (𝑢𝑏
) and lower bound (𝑙𝑏), population size (𝑁), number of
iteration 𝑇, scaling parameter 𝜁, evaporate rate ρ, step
size ℎ (or number of discrete value 𝑚)
2. Initialization
Assume a set of permissible discrete values 𝑚 for each
of the design variables
Initialize all discrete values 𝑚 of design variables equal
amounts of pheromone 𝜏

16. Ant Colony Optimization


17. Ant Colony Optimization


18. Ant Moves
 Four types:
 From home to food
 Goal has never been reached: moveStraightAwayFromAway();
 Goal reached: moveTowardAway();
 Back to home
 Goal has never been reached: moveFromFoodToHome();
 Goal reached: moveFromHomeToFood();
 Idea: generates several random moves and see which one is
the best among them.

19. Applications
 Traveling Salesman Problem
 Quadratic Assignment Problem
 Network Model Problem
 Vehicle routing
 Scheduling
 Telecommunication Network
 Graph Coloring
 Water Distribution Network
etc . . .

20. Traveling Salesman Problem
TSP PROBLEM : Given N cities, and a distance function d between cities,
find a tour that:
1. Goes through every city once and only once
2. Minimizes the total distance.
• Problem is NP-hard
• Classical combinatorial
optimization problem to
test.

21. ACO for Traveling Salesman Problem
The TSP is a very important problem in the context of
Ant Colony Optimization because it is the problem to
which the original AS was first applied, and it has later
often been used as a benchmark to test a new idea and
algorithmic variants.
The TSP was chosen for many reasons:
• It is a problem to which the ant colony metaphor
• It is one of the most studied NP-hard problems in the combinatorial optimization
• it is very easily to explain. So that the algorithm behavior is not obscured by
too many technicalities.

22. Algorithm for TSP
Initialize
Place each ant in a randomly chosen city
Choose NextCity(For Each Ant)
more cities
to visit
For Each Ant
Return to the initial cities
Update pheromone level using the tour cost for each ant
Print Best tour
yes
No
Stopping
criteria
yes
No

23. Iteration 1
A
E
D
C
B
1
[A]
5
[E]
3
[C]
2
[B]
4
[D]

24. Iteration 2
A
E
D
C
B
3
[C,B]
5
[E,A]
1
[A,D]
2
[B,C]
4
[D,E]

25. Iteration 3
A
E
D
C
B
4
[D,E,A]
5
[E,A,B]
3
[C,B,E]
2
[B,C,D]
1
[A,D,C]

26. Iteration 4
A
E
D
C
B
4
[D,E,A,B]
2
[B,C,D,A]
5
[E,A,B,C]
1
[A,DCE]
3
[C,B,E,D]

27. Iteration 5
A
E
D
C
B
1
[A,D,C,E,B]
3
[C,B,E,D,A]
4
[D,E,A,B,C]
2
[B,C,D,A,E]
5
[E,A,B,C,D]

28. Problem name Authors Algorithm name Year
Traveling salesman Dorigo, Maniezzo & Colorni AS 1991
Gamberdella & Dorigo Ant-Q 1995
Dorigo & Gamberdella ACS &ACS 3 opt 1996
Stutzle & Hoos MMAS 1997
Bullnheimer, Hartl & Strauss ASrank 1997
Cordon, et al. BWAS 2000
Quadratic assignment Maniezzo, Colorni & Dorigo AS-QAP 1994
Gamberdella, Taillard & Dorigo HAS-QAP 1997
Stutzle & Hoos MMAS-QAP 1998
Maniezzo ANTS-QAP 1999
Maniezzo & Colorni AS-QAP 1994
Scheduling problems Colorni, Dorigo & Maniezzo AS-JSP 1997
Stutzle AS-SMTTP 1999
Barker et al ACS-SMTTP 1999
den Besten, Stutzle & Dorigo ACS-SMTWTP 2000
Merkle, Middenderf & Schmeck ACO-RCPS 1997
Vehicle routing Bullnheimer, Hartl & Strauss AS-VRP 1999
Gamberdella, Taillard & Agazzi HAS-VRP 1999
ACO Algorithms : An Overview

29. Problem name Authors Algorithm name Year
Connection-oriented Schoonderwood et al. ABC 1996
network routing White, Pagurek & Oppacher ASGA 1998
Di Caro & Dorigo AntNet-FS 1998
Bonabeau et al. ABC-smart ants 1998
Connection-less Di Caro & Dorigo AntNet & AntNet-FA 1997
network routing Subramanian, Druschel & Chen Regular ants 1997
Heusse et al. CAF 1998
van der Put & Rethkrantz ABC-backward 1998
Sequential ordering Gamberdella& Dorigo HAS-SOP 1997
Graph coloring Costa & Hertz ANTCOL 1997
Shortest common supersequence Michel & Middendorf AS_SCS 1998
Frequency assignment Maniezzo & Carbonaro ANTS-FAP 1998
Generalized assignment Ramalhinho Lourenco & Serra MMAS-GAP 1998
Multiple knapsack Leguizamon & Michalewicz AS-MKP 1999
Optical networks routing Navarro Varela & Sinclair ACO-VWP 1999
Redundancy allocation Liang & Smith ACO-RAP 1999
Constraint satisfaction Solnon Ant-P-solver 2000
ACO Algorithms : An Overview cont…

30. Advantages
 Positive Feedback accounts for rapid discovery of good
solutions
 Distributed computation avoids premature convergence
 The greedy heuristic helps find acceptable solution in the
early solution in the early stages of the search process.
 The collective interaction of a population of agents.

31. Disadvantages
 Slower convergence than other Heuristics
 Performed poorly for TSP problems larger than 75
cities.
 No centralized processor to guide the AS towards good
solutions

32. Conclusion
 ACO is a recently proposed metaheuristic approach for
solving hard combinatorial optimization problems.
 Artificial ants implement a randomized construction
heuristic which makes probabilistic decisions.
 The a cumulated search experience is taken into account by
the adaptation of the pheromone trail.
 ACO Shows great performance with the “ill-structured”
problems like network routing.
 In ACO Local search is extremely important to obtain good
results.